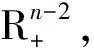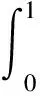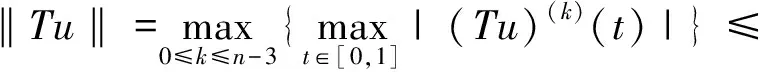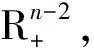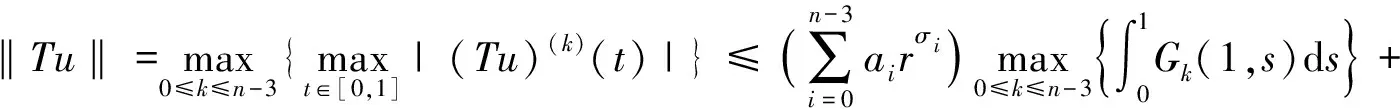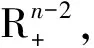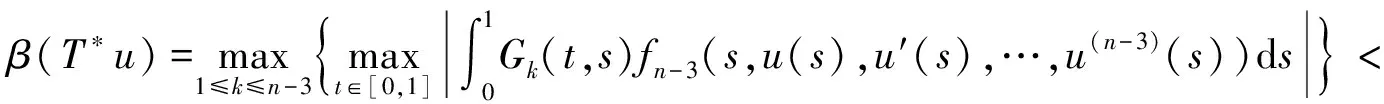一類分?jǐn)?shù)階微分方程邊值問(wèn)題正解的存在性
馮 立 杰
(天津大學(xué)數(shù)學(xué)學(xué)院,天津 300350)
0 引言
近年來(lái),分?jǐn)?shù)階微分方程受到了廣泛關(guān)注.與整數(shù)階微分方程相比,分?jǐn)?shù)階微分方程應(yīng)用范圍更廣,其在物理學(xué)、生物學(xué)、分析化學(xué)等領(lǐng)域發(fā)揮了重要的作用.[1-2]許多學(xué)者對(duì)分?jǐn)?shù)階微分方程進(jìn)行了深入的研究,取得了豐碩的成果.[3-7]
文獻(xiàn)[7]運(yùn)用單調(diào)迭代法,研究了分?jǐn)?shù)階微分方程邊值問(wèn)題
本文考慮非線性分?jǐn)?shù)階微分方程邊值問(wèn)題
(1)

1 預(yù)備知識(shí)
定義1[1]函數(shù)y:(0,+∞)→R的階數(shù)為α>0的Riemann-Liouville分?jǐn)?shù)階積分定義為
這里等式右邊是在(0,+∞)上逐點(diǎn)定義的.
定義2[1]函數(shù)y:(0,+∞)→R的階數(shù)為α>0的Riemann-Liouville分?jǐn)?shù)階導(dǎo)數(shù)定義為
其中:n=[α]+1,[α]表示α的整數(shù)部分;右邊在(0,+∞)上是逐點(diǎn)定義的.
引理1[1]假設(shè)y∈C(0,1)∩L1(0,1)且α>0,則
其中ci∈R,i=1,2,…,n,n如定義2所述.
引理2[1]假設(shè)y∈L1([0,1],R),且p>q>0,則對(duì)任意的t∈[0,1],有:
引理3給定y∈C[0,1],n-1<α≤n,β>0,則分?jǐn)?shù)階微分方程
(2)
(3)
的唯一解為

其中
(4)
這里d=[Γ(α+β)-Γ(α-n+2)ρηα+β-1]-1>0.
證明根據(jù)引理1可知方程(2)的一般解為
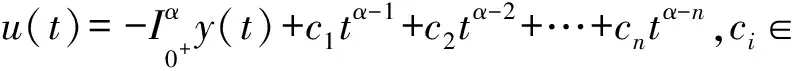
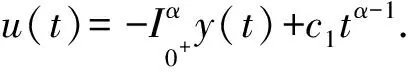
因此
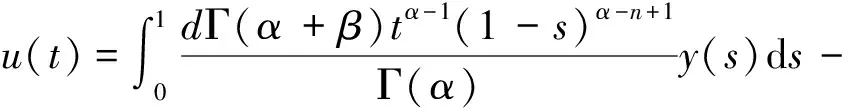
(5)
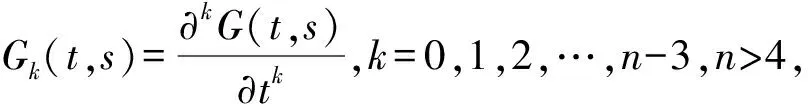
(6)
引理4函數(shù)Gk(t,s)有以下性質(zhì):
(ⅰ)Gk(t,s)是連續(xù)函數(shù),并且滿足Gk(t,s)≥0,t,s∈[0,1],k=0,1,2,…,n-3;
(ⅱ) 對(duì)任意的t,s∈[0,1],有tα-k-1Gk(1,s)≤Gk(t,s)≤Gk(1,s),k=0,1,2,…,n-3.
證明(ⅰ) 由等式(6)可知Gk(t,s)為連續(xù)的.
當(dāng)0≤s≤min{t,η}≤1時(shí),
當(dāng)0≤t≤s≤η≤1時(shí),
當(dāng)0<η≤s≤t≤1時(shí),
當(dāng)0 (7) 另外,顯然有Gk(t,s)≥tα-k-1Gk(1,s).結(jié)論證畢. 引理5[8](Schauder不動(dòng)點(diǎn)定理) 設(shè)U是Banach空間E中的一個(gè)非空有界閉凸子集,T:U→U是全連續(xù)算子,則T在U中至少存在一個(gè)不動(dòng)點(diǎn). 設(shè)E是一個(gè)Banach空間,P?E是一個(gè)錐.假設(shè)α,β:E→R+是兩個(gè)連續(xù)的凸泛函,并且滿足:對(duì)于u∈E,λ∈R有α(λu)=|λ|α(u),β(λu)=|λ|β(u);當(dāng)u∈E時(shí),‖u‖≤kmax{α(u),β(u)};當(dāng)u1,u2∈P,u1≤u2時(shí),α(u1)≤α(u2),其中k是一個(gè)常數(shù). 引理6[9]令r2>r1>0,L>0都是常數(shù), Ωi={u∈E|α(u) 是E上的兩個(gè)有界開(kāi)集.記Di={u∈E|α(u)=ri}.假設(shè)T:P→P是全連續(xù)算子并且滿足: (ⅰ)α(Tu) (ⅱ)β(Tu) 定義E=Cn-3[0,1],定義范數(shù) 則(E,‖·‖)是一個(gè)Banach空間. 定義如下形式的錐: P={u∈E|u(k)(t)≥0,u(k)(t)≥tα-k-1‖u(k)‖0,t∈[0,1],k=0,1,2,…,n-3; u(i)(0)=0,i=0,1,2,…,n-4}. 在P上定義算子T為 (8) 則算子T的不動(dòng)點(diǎn)即為邊值問(wèn)題(1)的解. 證明首先證明算子T:P→P.根據(jù)引理4,有(Tu)(k)(t)≥0,?t∈[0,1],k=0,1,2,…,n-3.另外, 且 因此算子T:P→P. 下面證明算子T是全連續(xù)的.由于函數(shù)G,f都是連續(xù)的,所以算子T是連續(xù)的.設(shè)Ω為E中的任意有界集,則存在常數(shù)N>0,對(duì)?u∈Ω,有‖u‖≤N.記 對(duì)?u∈Ω,由引理4可知 所以,T(Ω)為一致有界的. 另一方面,?t1,t2∈[0,1],不妨設(shè)t1 當(dāng)t1→t2時(shí),上述不等式趨于0.因此T(Ω)為等度連續(xù)的. 則邊值問(wèn)題(1)至少存在一個(gè)正解. 證明定義有界集Br={u∈P|‖u‖≤r},其中: 下證T:Br→Br.如果u∈Br,有 因此 又根據(jù)引理7知T:Br→Br是全連續(xù)的,從而由Schauder不動(dòng)點(diǎn)定理可得邊值問(wèn)題(1)至少存在一個(gè)正解. 定義泛函 則有: α(λu)=|λ|α(u),β(λu)=|λ|β(u),λ∈R; 當(dāng)u1,u2∈P,u1≤u2時(shí),α(u1)≤α(u2). 記 其中0<γ<1. 定理2假設(shè)L>r2>γα-1r2>r1>0,其中0<γ<1為常數(shù).f(t,u0,u1,…,un-3)滿足以下條件: (H1)f(t,u0,u1,…,un-3) (H2)f(t,u0,u1,…,un-3)≥Dr2,(t,u0,…,uk,…,un-3)∈[γ,1]×[γα-1r2,r2]×…×[γα-k-1r2,L]×…×[γα-n+2r2,L]; (H3)f(t,u0,u1,…,un-3) 則邊值問(wèn)題(1)至少有一個(gè)正解u(t)滿足 r1<α(u) 證明對(duì)f做如下修改: 依次進(jìn)行下去有 考慮邊值問(wèn)題 (9) 定義 Ω1={u∈E|α(u) 與 Ω2={u∈E|α(u) 為E中的兩個(gè)有界開(kāi)集.記 D1={u∈E|α(u)=r1}, D2={u∈E|α(u)=r2}. 分三步對(duì)定理進(jìn)行證明. 步驟一:對(duì)u∈D1∩P有α(u)=r1,0≤u(t)≤r1. 由(H1), 對(duì)u∈D2∩P,有α(u)=r2,‖u‖0=r2,0≤u(t)≤r2,t∈[0,1].另u(i)(0)=0,i=0,1,2,…,n-4. 由 可得 ‖u(i)‖0≤‖u(i+1)‖0,‖u(k)‖0≥‖u‖0=r2,k=1,2,…,n-3. 因此 u(k)(t)≥γα-k-1‖u(k)‖0≥γα-k-1r2,t∈[γ,1],k=0,1,2,…,n-3. 其中0<γ<1.由(H2), 步驟二:根據(jù)(H3),對(duì)于u∈P有 步驟三:由α(u)的定義,存在一個(gè)非負(fù)函數(shù)p∈{(Ω2∩P)
主站蜘蛛池模板:
亚洲精品成人片在线观看|
色妺妺在线视频喷水|
91精品国产自产在线老师啪l|
亚洲人成影院在线观看|
美女一区二区在线观看|
波多野结衣无码AV在线|
亚洲精品少妇熟女|
国产亚洲第一页|
超碰免费91|
欧美区国产区|
AV在线天堂进入|
992Tv视频国产精品|
91国内视频在线观看|
av性天堂网|
国产黄色免费看|
波多野结衣视频网站|
波多野结衣在线se|
日本精品中文字幕在线不卡|
国产激情第一页|
成人精品视频一区二区在线|
国产成人综合日韩精品无码首页|
国产区91|
综合色在线|
亚洲国产综合自在线另类|
国产精品男人的天堂|
99这里只有精品免费视频|
国产91色在线|
色悠久久综合|
青青操视频在线|
国产污视频在线观看|
91丝袜在线观看|
久久精品国产999大香线焦|
国产全黄a一级毛片|
欧美日韩免费观看|
蜜芽一区二区国产精品|
免费国产不卡午夜福在线观看|
国产精品久线在线观看|
素人激情视频福利|
国产黑丝一区|
亚洲国产精品久久久久秋霞影院|
av一区二区人妻无码|
98精品全国免费观看视频|
久久青草精品一区二区三区|
少妇人妻无码首页|
99re热精品视频中文字幕不卡|
99中文字幕亚洲一区二区|
99国产精品免费观看视频|
激情综合图区|
992Tv视频国产精品|
日本欧美中文字幕精品亚洲|
全部毛片免费看|
久久精品国产91久久综合麻豆自制|
草逼视频国产|
播五月综合|
欧美一级99在线观看国产|
欧美福利在线播放|
国产在线精彩视频二区|
欧洲极品无码一区二区三区|
无码内射中文字幕岛国片|
亚洲国产精品不卡在线|
亚洲成人在线网|
免费AV在线播放观看18禁强制|
成人伊人色一区二区三区|
2019年国产精品自拍不卡|
日本一区高清|
国产成人精品视频一区二区电影|
国产人人乐人人爱|
69国产精品视频免费|
国产精品尤物铁牛tv|
国产你懂得|
自偷自拍三级全三级视频|
996免费视频国产在线播放|
少妇精品在线|
网友自拍视频精品区|
午夜小视频在线|
国产精品第页|
亚洲一区毛片|
99热最新在线|
天天干天天色综合网|
99久久这里只精品麻豆|
国模私拍一区二区|
国产又爽又黄无遮挡免费观看
|
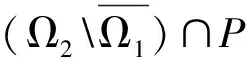
2 主要結(jié)果