深海油田電潛泵長距離變頻驅動系統分數階建模及起動電壓降分析

夏鵬程，梁志珊，左信

中國石油大學(北京)地球物理與信息工程學院，北京 102249

0 引言

在深海油田開發中，電潛泵等水下采油設備的供電電源和變頻器通常放置于海上采油平臺，變頻器和電機之間存在幾十公里的距離，需要用長電纜連接(圖1)。這樣，就由變頻器—長電纜—電潛泵構成了深海油田IEESP系統(Inverter-Electric cable-Electric submersible pump，簡稱IEESP)。

目前，實現了從海上平臺變頻器到電潛泵長距離供電的有北海北部的Otter油田，其電纜長度達到21 k m[1]。BP石油公司在墨西哥灣最長供電距離為29 k m的變頻器系統[2]。西門子公司的ESP 30 km長距離供電案例是最新的最長記錄。國內流花油田變頻器與電潛泵距離長達15.5 km[3]。隨著海底油田的進一步開發與生產，實際工程要求使用比已有IEESP更長的海底電纜。

IEESP系統整數階模型研究發現，采取變頻器長電纜驅動技術，雖然帶來了諧波污染和PWM脈沖波電壓等問題[4-7]，但是實現了軟啟動，消除了大啟動電流對電泵機組的機械和電力沖擊[8]。然而，由于電纜距離過長以及定子電阻電壓損耗嚴重，電機磁通經常出現嚴重衰減，導致無法正常起動。所以，通常需要采取對長電纜以及定子電阻的壓降進行補償，保證電動機正常起動[9]。當前，某海洋油田工程面臨電潛泵經40 km長電纜變頻驅動是否可行的難題，包括：長電纜電壓降的變化規律，變頻器輸出起動電壓頻率和升壓變壓器補償電壓設計等問題。對于這些實際工程問題，國內外還沒有相應的行業標準和規范，需要進行研究和探索。

圖1 深海油田電潛泵長距離變頻驅動系統Fig. 1 Long distance electric submersible pump frequency drive system in deep sea oil fi eld

分數階微積分(Fractional Calculus，簡稱FC)提供了一個更精確的物理系統模型，能夠反映系統內在的耗散過程，特別是在電路中，分數階模型已經廣泛用于模擬電路和元件(電阻、電感、電容、多米諾梯子，樹形結構，憶阻器等等)。常用FC定義有Riemann-Liouville (簡稱RL)、Liouville-Caputo (簡稱LC)[10]。電容、電感和電阻存在不同時間尺度上的波動或分形特征。電氣元件異質性的存在，會造成不可逆的耗散效應。由于導體的趨膚效應和介質的松弛現象，在描述電壓電流波傳播過程時，電纜和傳輸線分數階模型比整數階模型更有優勢[11-12]。已有研究表明，實際系統在理論上都應該是分數階次的[13-16]，只是由于分數階理論的滯后而使得所使用的數學模型都是整數階次。分數階模型對于更長距離的IEESP系統有多大影響？這是IEESP系統設計和運行非常關注的問題。

常用的RL和LC分數階定義的缺點是他們的內核具有奇異性，這個內核包括記憶效應，因此，這兩種定義都不能準確描述記憶的全部影響。在傳統的Caputo分數階導數定義中，分數階電容參數的物理單位[17-18]是F/s1-n，分數階電感參數的物理單位[19]是VsαA-1。在電容參數和電感參數的物理單位中含有分數階階次n和α，這意味著它們的物理單位是隨分數階階次變化的。而整數階電容的物理單位是F(法拉)，整數階電感的物理單位是H(亨利)。很顯然，分數階與整數階定義下基本物理量的單位不一樣，使得分數階電容和分數階電感的物理含義有所不同。由于分數階階次是隨元件結構空間變化的，意味著含分數階階次的單位也是隨空間變化的。分數階憶阻器與電容電感串聯電路[20]、分數階LC串并聯電路[21-22]、LCL型電路[23]、濾波電路[24-25]和分數階模擬電容和模擬電感電路[26]等已有的系統理論研究均忽略了電容電感的物理單位問題。作者認為分數階和整數階微積分作為一種數學分析計算工具，在使用過程中對于電感元件和電容元件物理現象與元件參數應該是一一對應統一的。

Caputo和Fabrizio提出了一個新的分數階導數定義，即Caputo-Fabrizio分數階(簡稱CF)[27]，無奇異的內核，這個定義可以描述與損傷、疲勞以及材料其他非均質性相關的力學性能。這個定義的新穎之處在于，它們具有規則的核心，不含奇異核，可以視為一個濾波調節器[28]。Caputo-Fabrizio分數階定義具有廣泛的應用[29-30]。

本文針對深海油田40 km長電纜變頻驅動電潛泵，分數階的電感和電容物理單位與整數階不統一等問題，用Caputo-Fabrizio分數階導數定義建立了物理單位統一的IEESP系統分數階模型，研究了IEESP系統分數階系統起動電壓降的變化規律。通過分數階模型與整數階模型的對比分析，改進了升壓補償措施，抵消了起動電壓降的影響。

1 長電纜分數階模型

模型采用均勻傳輸線模型來分析變頻器輸出電壓波的傳輸過程。均勻傳輸線由一系列集總元件電阻、電感、電容和電導構成，即假設它是由許多無窮小的長度dx組成的，每個長度元dx具有電阻R0dx和電感L0dx，而兩導線間具有電容C0dx和電導G0dx(圖2)。

圖2中，R0為長線電纜每單位長度具有的電阻，其單位為Ω/km；L0為長線電纜每單位長度具有的電感，其單位為mH/km；C0為每單位長度長線電纜兩線之間的電容，其單位為uF/km；G0為每單位長度長線電纜兩線之間的電導，其單位為S/km。

電力電纜系統的傳輸線方程，在頻域中表示如下：

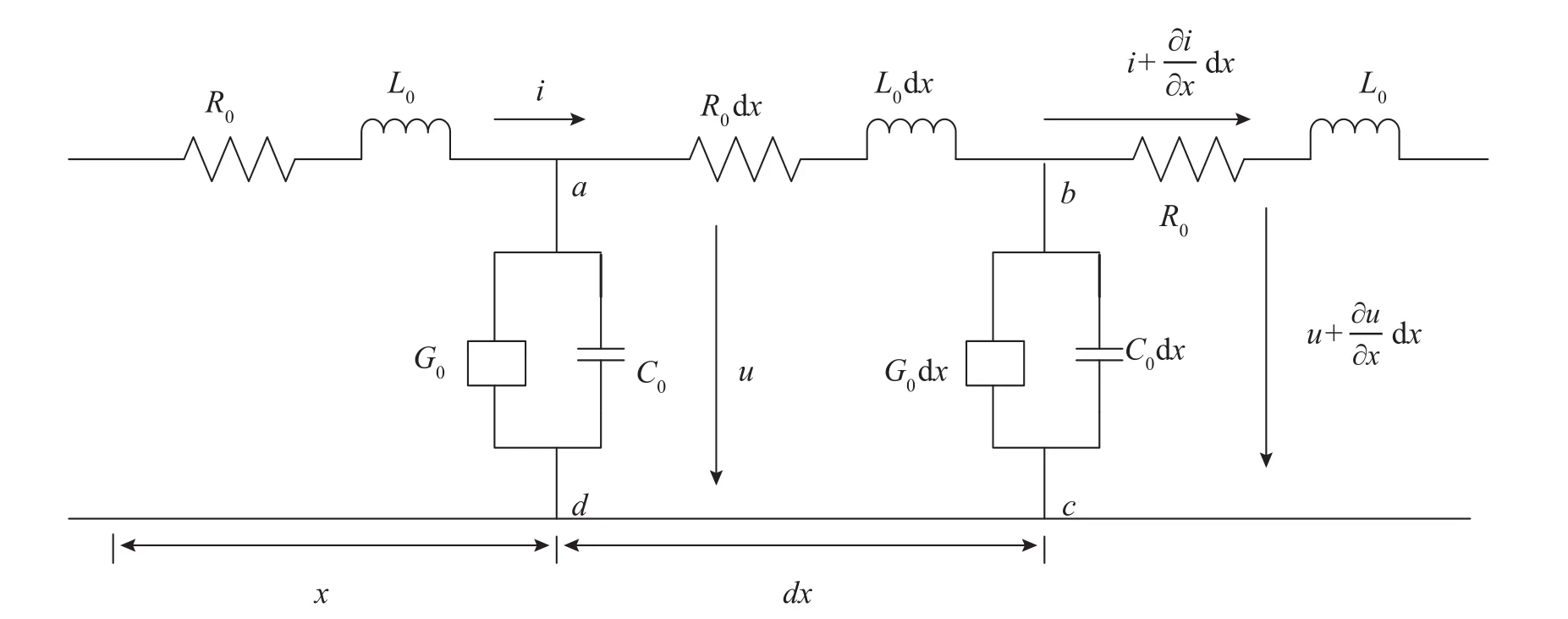
圖2 均勻長線電纜模型Fig. 2 Model of uniform long line cable

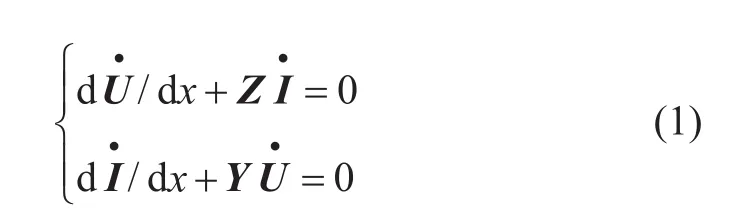
其中，為傳輸線上任意一點電壓，V；為傳輸線上任意一點電流，A；Z為傳輸線單位長度的阻抗矩陣，Ω/km；Y為傳輸線單位長度的導納，S/km。Z=R+jωL，R為傳輸線單位長度的電阻，Ω/km；L為傳輸線單位長度的電感，H/km。一般情況下，由于導體與大地的集膚效應，Z的參數都會隨頻率變化。Y=G+jωC，G為傳輸線單位長度的電導，S/km；C為傳輸線單位長度的電容，F/km，Y一般看做是非頻變的。

1.1 建模理論

傳統的電感元件和電容元件建模使用時間函數f(t)的Liouville-Caputo分數導數(LC)，定義如下

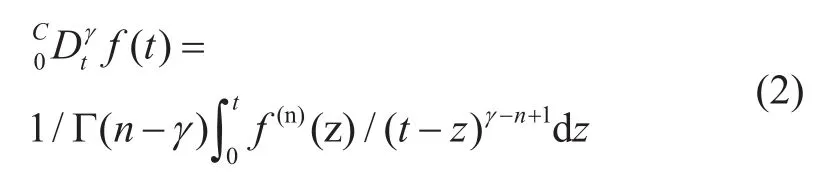
本文引入Caputo-Fabrizio分數導數(CF)，定義如下是關于t的LC導數，nN

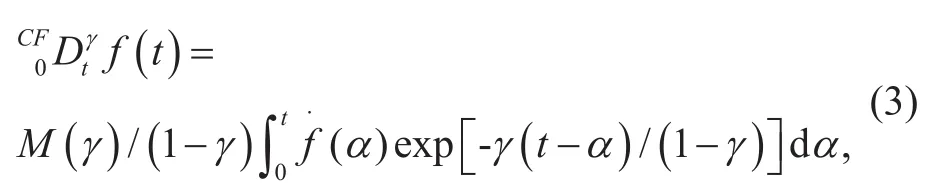
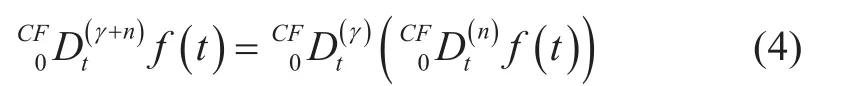
CF分數階導數式(4)的拉普拉斯變換定義如下

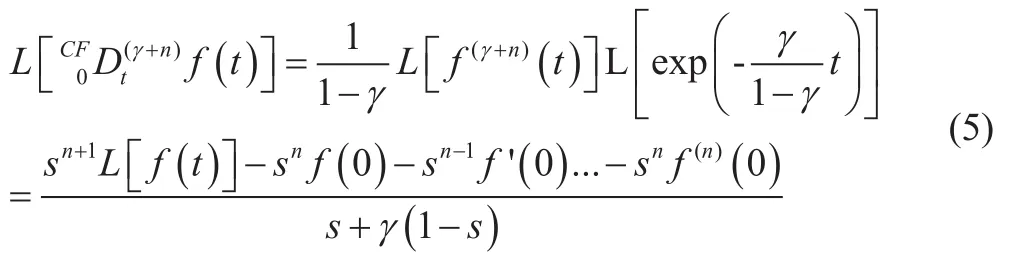
對于這種在時域上的方程，可以使用Laplace變換

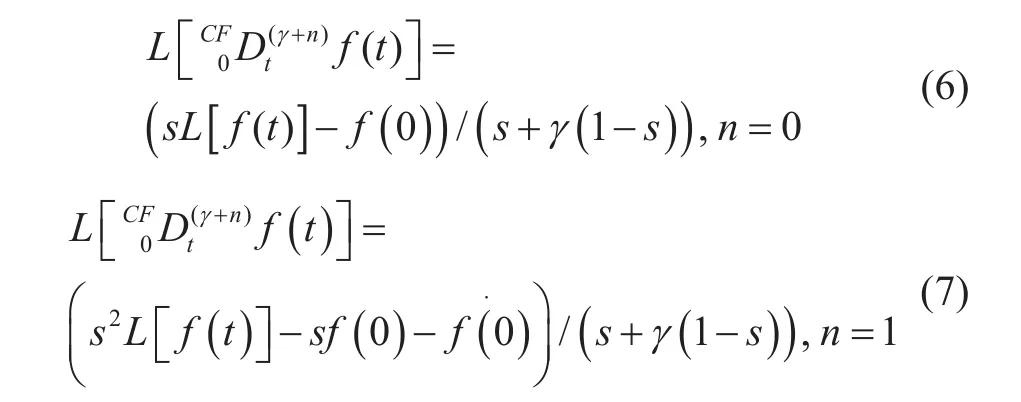
用分數算子代替整數算子

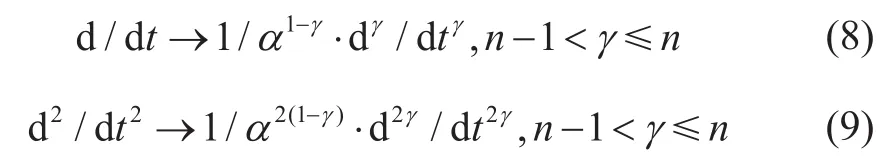
其中n為整數，且α的物理單位是秒的分數維。這樣就抵消了分數階導數作用于時間t產生的物理單位秒的分數維。傳統常用的RL和LC分數階定義是把電容電感的物理單位乘上一個秒的分數維來平衡單位統一的問題，但那樣做使得分數階電容量和電感量與整數階的數值不一樣了，單位也不同，無法確定分數階電容量和電感量與整數階是否存在一對一等效關系。而本文的CF分數階導數定義就解決了這樣問題，統一了分數階和整數階的基本物理量單位，使得分數階電容量和電感量與整數階的一樣，奠定了對比分析的統一參考平臺。當γ=1時，式(8)和(9)成為一個普通的導數。

1.2 建模方法

我們將這種方法應用于電纜模型RLCG電路中。假設將電纜平均分成n段，如圖1所示，考慮在某一個RLCG單元中，由基爾霍夫定律可得

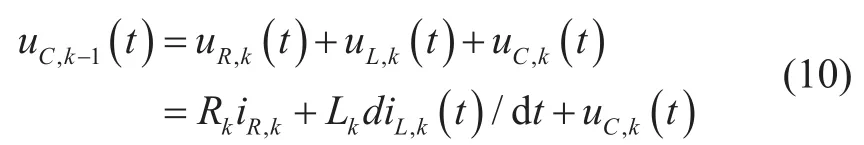
其中，k∈[1,n]，首端uC,0(t) =vin為變頻器輸出電壓

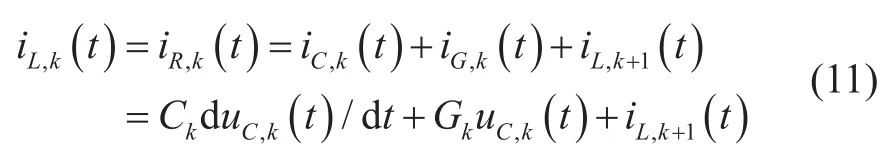
其中，k∈[1,n]，末端iL,n+1(t) =is為電機定子電流。

把式(11)代入式(10)得到

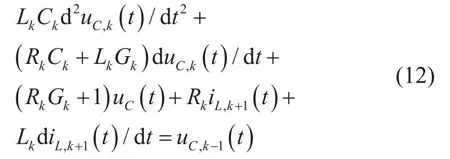
根據(8)和(9)的變換，由(12)可得分數階的表達式為

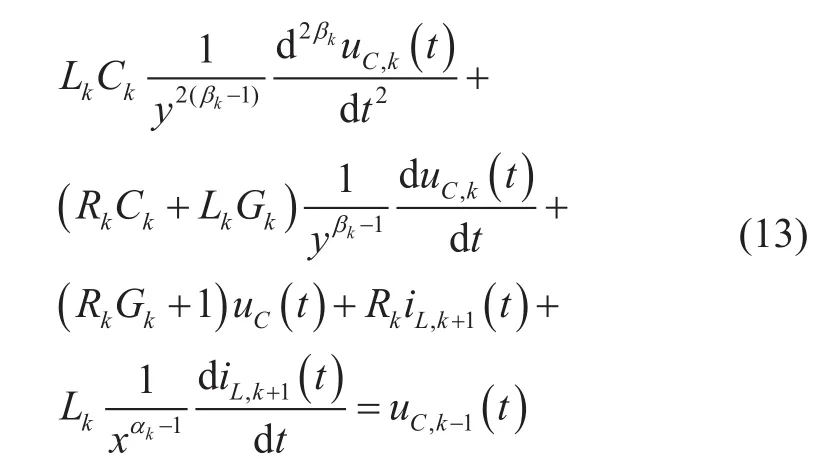
設分數階角頻率ωγ，分數階時間常數τγ

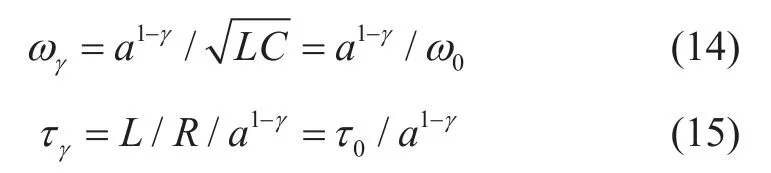
則式(13)可簡化為

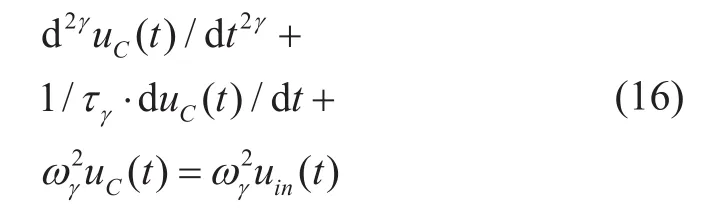
建立電纜分布參數分數階微分方程組來描述傳輸線的電壓電流波

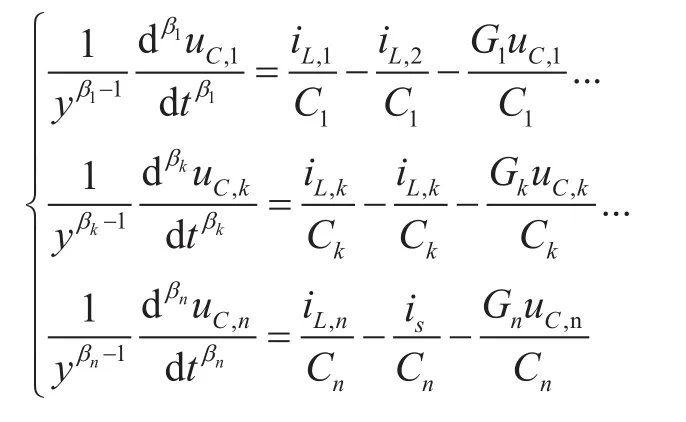
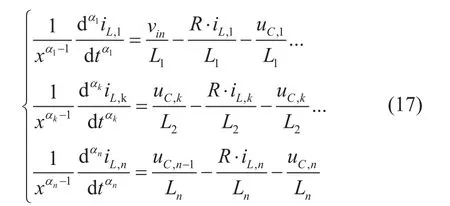
因此，當電潛泵起動時長電纜電壓降與起動電壓頻率、電纜長度、電纜阻抗特性、電機負載阻抗特性以及分數階階次等有關。

2 IEESP系統仿真與分析

2.1 系統仿真

基于改進的Oustaloup濾波器分數階微積分算法和式(17)構建Matlab/Simulink數學模型[8]。在IEESP分數階系統中，電潛泵起動電壓降受到起動電壓頻率、電纜長度、電纜分布電阻、電纜分布電感、電纜分布電容參數、負載特性阻抗和分數階階次等7個參數的影響。

某深海油田工程提供了海底電纜和井下電纜的典型參數(表1)。在模型中電纜分布電阻為0.34 Ω/km、電纜分布電感為0.38 mH/km、電纜分布電容為0.29 μF/km、變頻器輸出電壓為6000 V，電潛泵起動時的等效阻抗為1.36 Ω。當模型其他參數變化時，整數階模型中的電感電容參數階次是1，分數階模型中電感電容參數階次是0.8。

(1)起動電壓頻率

在電潛泵起動的瞬態過程中，起動電壓頻率越大，長電纜電壓降瞬態幅值越小(圖3)。

分數階模型仿真表明：當起動電壓正弦波頻率f1～f5從10 Hz遞增到50 Hz時，長電纜電壓降幅值Ufo(U1～U5)從 5074 V減小到 4592 V，是變頻器輸出電壓(U0)的84.57%～76.53%。整數階模型仿真表明：長電纜電壓降幅值Uio(U1～U5)從5121 V減小到2771 V ，是電源電壓的85.35%～46.18%。隨著起動電壓頻率增大，整數階模型與分數階模型的相對偏差絕對值|Uio-Ufo|/U0越來越大，分別是0.78%、10.07%、19.35%、25.93%、30.30%。起動電壓頻率越高，分數階模型由于考慮了趨膚效應，計算的電壓波在長電纜上的傳播損耗更高，而整數階模型沒有包含這部分損耗，所以計算出的長電纜電壓降比分數階模型的計算結果小。說明分數階模型比整數階模型能更準確地反映IEESP系統電潛泵變頻起動過程中長電纜電壓降和不可逆的耗散效應。

表1 深海電纜典型參數Table 1 Typical parameters of deep-sea cable

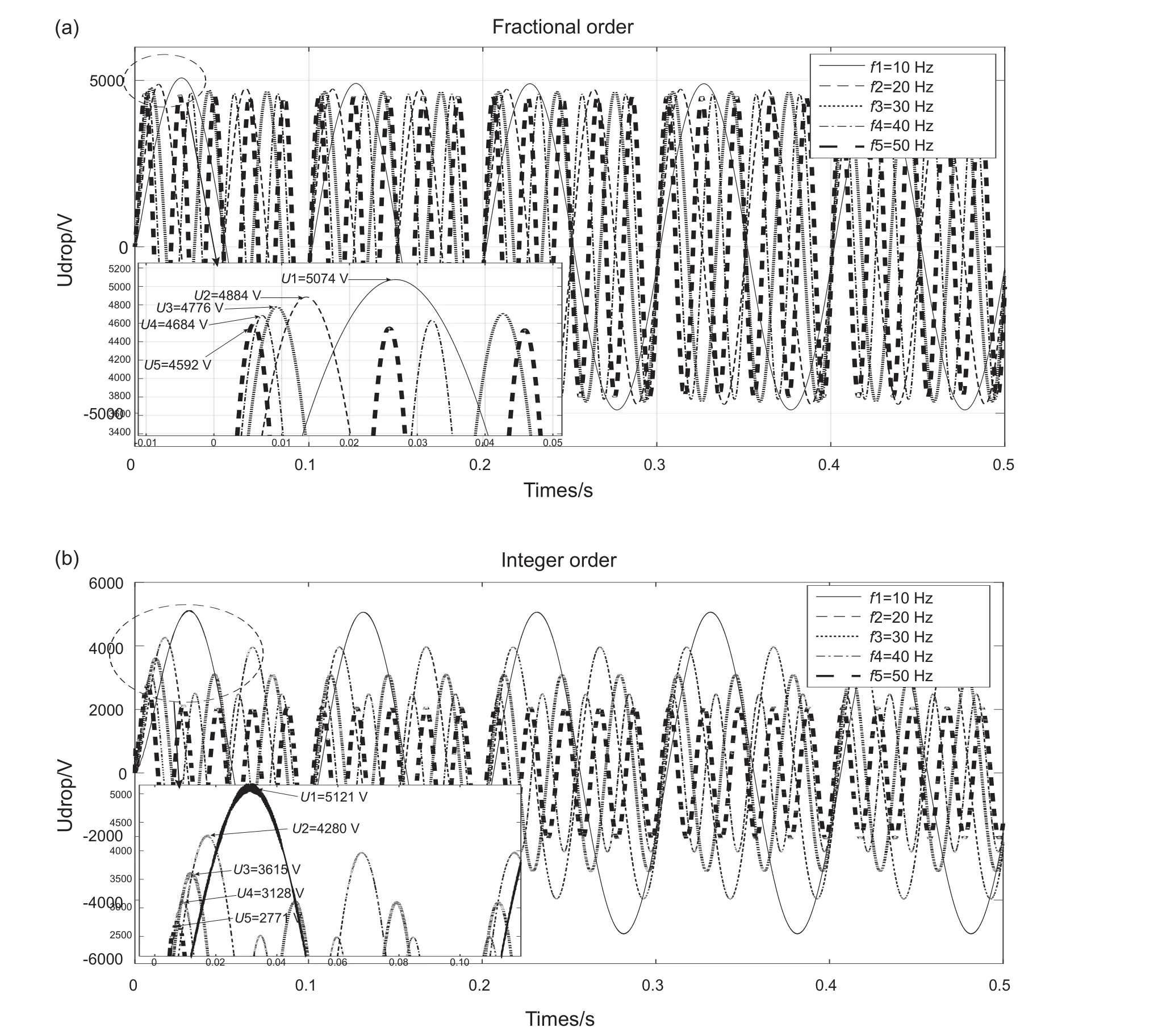
圖3 起動電壓頻率對電壓降的影響(a)分數階(b)整數階Fig. 3 The effect of starting frequency on voltage drop: (a) fractional order;(b) integer order

(2)電纜長度

在電潛泵起動的瞬態過程中，電纜越長，長電纜電壓降瞬態幅值越大(圖4)。

分數階模型仿真表明：當電纜長度l1～l5從20 km遞增到60 km時，長電纜電壓降幅值Ufo(U1～U5)從4373 V 增大到5354 V，是U0的72.88%～89.23%。整數階模型仿真表明：長電纜電壓降幅值Uio(U1～U5)從4251 V 增大到5455 V，是U0的70.85%～90.92%。隨著電纜長度增加，整數階模型與分數階模型的相對偏差絕對值|Uio-Ufo|/U0先減小后增大，分別是2.03%、0.30%、0.78%、1.22%、1.68%。

(3)電纜分布電阻

在電潛泵起動的瞬態過程中，電纜分布電阻越大，長電纜電壓降瞬態幅值越大(圖5)。

分數階模型仿真表明：當電纜分布電阻R1～R5從0.14 Ω/km遞增到0.54 Ω/km時，長電纜電壓降幅 值Ufo(U1～U5)從 4191 V增 大 到 5385 V， 是U0的69.85%～89.75%。整數階模型仿真表明：長電纜電壓降幅值Uio(U1～U5) 從3872 V增大到5517 V，是U0的64.53%～91.95%。隨著電纜分布電阻增大，整數階模型與分數階模型的相對偏差絕對值|Uio-Ufo|/U0先減小后增大，分別是5.32%、0.88%、0.80%、1.8%、2.20%。

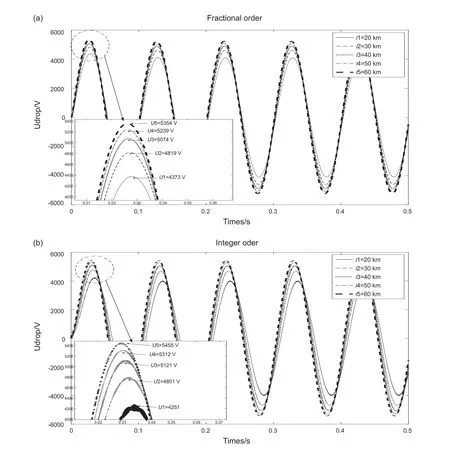
圖4 電纜長度對電壓降的影響(a)分數階(b)整數階Fig. 4 The effect of cable length on voltage drop: (a) fractional order; (b) integer order

(4)電纜分布電感

在電潛泵起動的暫態過程中，電纜分布電感越大，長電纜電壓降瞬態幅值越大(圖6)。

分數階模型仿真表明：當電纜分布電感L1～L5從0.18 mH/km遞增到0.58 mH/km時，長電纜電壓降幅值Ufo(U1～U5)從5070 V增大到5077 V，變化幅度不大，是U0的84.5%～84.62%。說明長電纜電壓降對電纜分布電感參數不敏感。整數階模型仿真表明：長電纜電壓降幅值Uio(U1～U5)從5164 V減小到5069 V，是U0的86.07%～84.48%。電纜分布電感參數對電纜電壓降的影響出現反常現象。隨著電纜分布電感的增大，分數階模型的電壓降變化趨勢是遞增的，整數階模型的電壓降變化趨勢是遞減的。隨著電纜分布電感增大，整數階模型與分數階模型的相對偏差絕對值|Uio-Ufo|/U0越來越小，分別是1.57%、0.97%、0.78%、0.50%、0.13%。

(5)電纜分布電容

在電潛泵起動的瞬態過程中，電纜分布電容越大，長電纜電壓降幅值瞬態幅值越小(圖7)。

分數階模型仿真表明：當電纜分布電容C1～C5從 0.09 μF/km遞增到 0.49 μF/km時，長電纜電壓降幅值Ufo(U1～U5)從 5073.85 V減小到 5073.72 V，變化幅度不大，是U0的84.564%～84.562%。說明長電纜電壓降對電纜分布電容參數不敏感。整數階模型仿真表明：長電纜電壓降幅值Uio(U1～U5)從5138 V減小到5105 V，是U0的85.63%～85.08%。隨著電纜分布電感增大，整數階模型與分數階模型的相對偏差絕對值|Uio-Ufo|/U0越來越小，分別是1.07%、0.95%、0.79%、0.67%、0.52%。

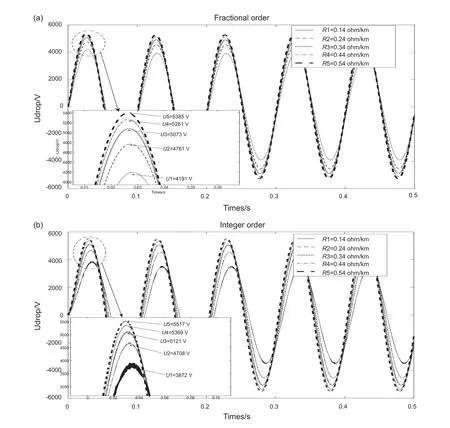
圖5 電纜分布電阻對電壓降的影響(a)分數階(b)整數階Fig. 5 The effect of cable distribution resistance on voltage drop: (a) fractional order ; (b) integer order

(6)負載電阻

在電潛泵起動的瞬態過程中，負載電阻越大，長電纜電壓降瞬態幅值越大(圖8)。

分數階模型仿真表明：當負載電阻Rm1～Rm5從0.36 Ω遞增到2.36 Ω時，長電纜電壓降幅值Ufo(U1～U5)從4514 V增大到5171 V，是U0的75.23%～86.18%。整數階模型仿真表明：長電纜電壓降幅值Uio(U1～U5)從4590 V 增大到5216 V，是U0的76.5%～86.93%。隨著負載電阻增大，整數階模型與分數階模型的相對偏差絕對值|Uio-Ufo|/U0越來越小，分別是1.27%、0.87%、0.80%、0.77%、0.75%。

(7)分數階階次

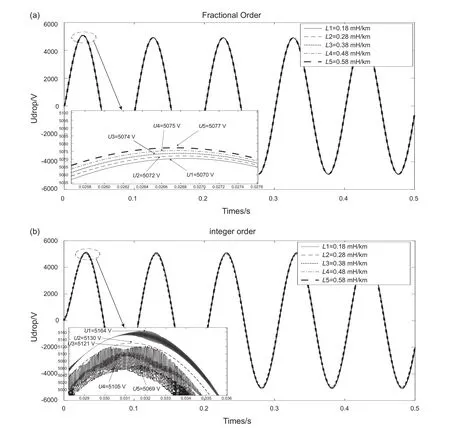
圖6 電纜分布電感對電壓降的影響(a)分數階(b)整數階Fig. 6 The effect of cable distributed inductance on voltage drop: (a) fractional order; (b) integer order

分析負載電感階次、電纜分布電感階次和電纜分布電容階次對長電纜電壓降的影響。

1)負載電感的分數階次

在電潛泵起動的瞬態過程中，負載電感的分數階次越大，長電纜電壓降瞬態幅值越小(圖9)。

電纜分數階模型仿真表明：當負載電感階次m1～m5從0.2遞增到1.0時，長電纜電壓降幅值Ufo(U1～U5)從5605 V減小到5073 V，是U0的93.42%～86.67%。但U4＜U5＜U3，而且電壓降相位發生了右移，1.0階次時比0.2階次的電壓降相位滯后7/50π。電纜整數階模型仿真表明：長電纜電壓降幅值Uio(U1～U5)從5599V減小到5037 V，是U0的93.32%～85.35%。但U4＜U5＜U3，而且電壓降相位發生了逐漸右移，階次1.0比0.2的長電纜電壓降相位滯后4/25π。隨著負載電感階次增大，整數階模型與分數階模型的相對偏差絕對值|Uio-Ufo|/U0越來越大，分別是0.10%、0.13%、0.25%、0.60%、1.32%。

2)電纜分布電感的分數階次

在電潛泵起動的瞬態過程中，電纜分布電感的分數階次越大，長電纜電壓降瞬態幅值先小幅增大后減小(圖10)。分數階模型仿真表明：當電纜分布電感分數階階次α1～ α5從0.5遞增到0.9時，長電纜電壓降幅值Ufo(U1～U5)分別是5074 V、5075.8 V、5076.2 V、5073.8 V、5064 V，是U0的84.57%～84.4%。

圖7 電纜分布電容對電壓降的影響(a)分數階(b)整數階Fig. 7 The effect of cable distributed capacitance on voltage drop:(a) fractional order; (b) integer order

3)電纜分布電容的分數階次

在電潛泵起動的瞬態過程中，隨電纜分布電容的分數階次增大，長電纜電壓降瞬態幅值先小幅增大后減小(圖11)。分數階模型仿真表明：當電纜分布電容分數階階次β1～ β5從0.5遞增到0.9時，長電纜電壓降Ufo(U1～U5)幅值分別是5074.05 V、5074.1 V、5074 V、5073.8 V、5073.2 V，是U0的84.57%～ 84.55%。

2.2 關于分數階與整數階模型問題的討論

對比IEESP系統分數階模型和整數階模型的仿真結果可知，電潛泵起動電壓降的變化規律如表2所示。

分數階模型和整數階模型的計算偏差來源于電感、電容元件的階次。在變頻器、長電纜和電潛泵的模型中，整數階的電感和電容只在理論上存在而在實際中并不存在，基于分數階微積分理論建立的電感和電容模型更能反映其實際系統的電特性，以往用來描述電感和電容電特性的整數階模型是不夠準確的，由此得到的某些結論甚至可能是錯誤的。

由表2可以看出：(1)當電纜分布電感變化時，分數階模型的長電纜電壓降的變化趨勢與整數階模型相反。(2)當電纜長度和電纜分布電阻參數發生變化時，分數階模型的長電纜電壓降與整數階模型的相對偏差絕對值呈現V形分段，先減小后增大。(3)電潛泵起動電壓降的變化規律可以為升壓變壓器補償電壓設計提供理論依據。從模型最大相對偏差推出，補償電壓應比傳統設計的高三分之一。

研究結果表明，基于Caputo-Fabrizio分數階微積分建立的IEESP系統分數階模型不含奇異核，統一了分數階電容電感參數與整數階的物理量綱，厘定了分數階模型與整數階模型計算對比平臺，比傳統模型能更加準確地描述深海長電纜電力傳輸特性。因此，采用Caputo-Fabrizio分數導數定義建立的長電纜分數階模型是合理的。

由表3可以看出，電纜長度l在20 km～60 km的范圍內，分數階模型計算出的電潛泵起動電壓降Ufo逐漸增大，但是起動電壓降的增幅ΔUfo越來越小，分別為446 V、225 V、165 V、115 V；增幅與變頻器輸出電壓的比值ΔUfo/U0也越來越小，分別是7.43%、4.25%、2.75%、1.92%。整數階模型計算出的電潛泵起動電壓降Uio逐漸增大，但是起動電壓降的增幅ΔUio越來越小，分別是550 V、320 V、191 V、143 V ；增幅與變頻器輸出電壓的比值ΔUio/U0也越來越小，分別是9.17%、5.33%、3.18%、2.38%。兩種模型對比發現，分數階模型比整數階模型計算的電潛泵起動電壓降更小，起動電壓降的增幅更小，增幅比也更小。根據分數階模型計算結果，電纜長度超過40 k m后，電潛泵起動電壓降的增量越來越小，升壓變壓器補償電壓的負擔也越來越小，補償電壓設計方案比較容易實現。

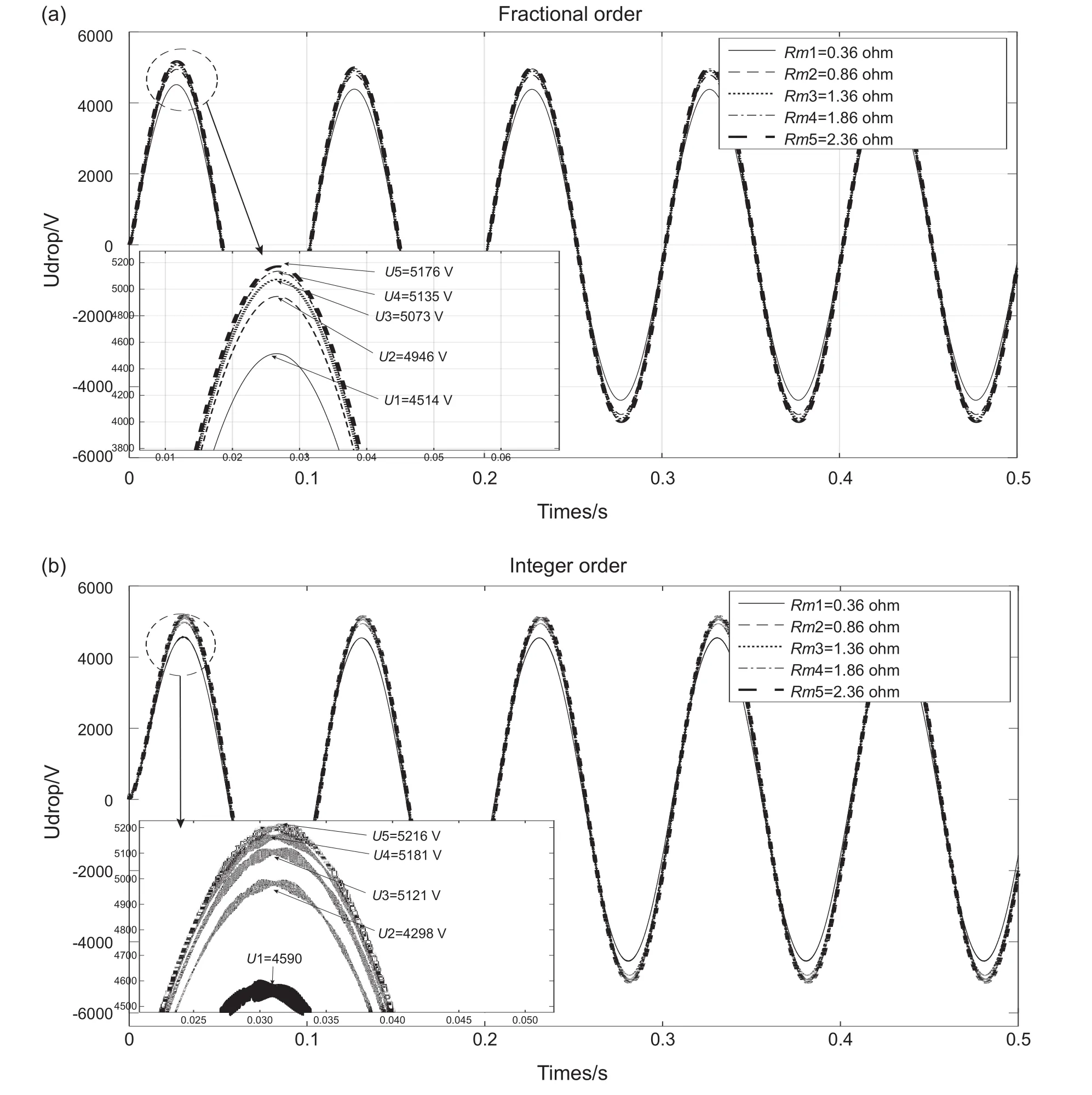
圖8 負載電阻對電壓降的影響(a)分數階(b)整數階Fig. 8 The effect of load resistance on voltage drop:(a) fractional order; (b) integer order

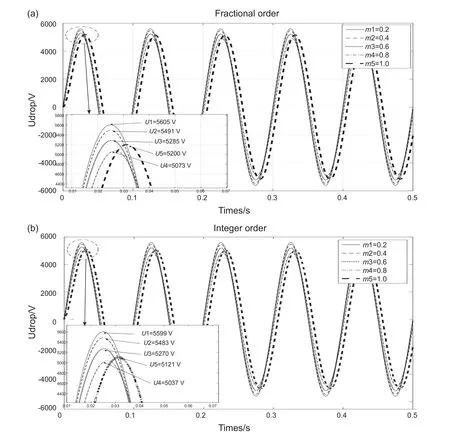
圖9 負載電感分數階次對電壓降的影響(a)分數階(b)整數階Fig. 9 The effect of load inductor fractional order on voltage drop:(a) fractional order ; (b) integer order

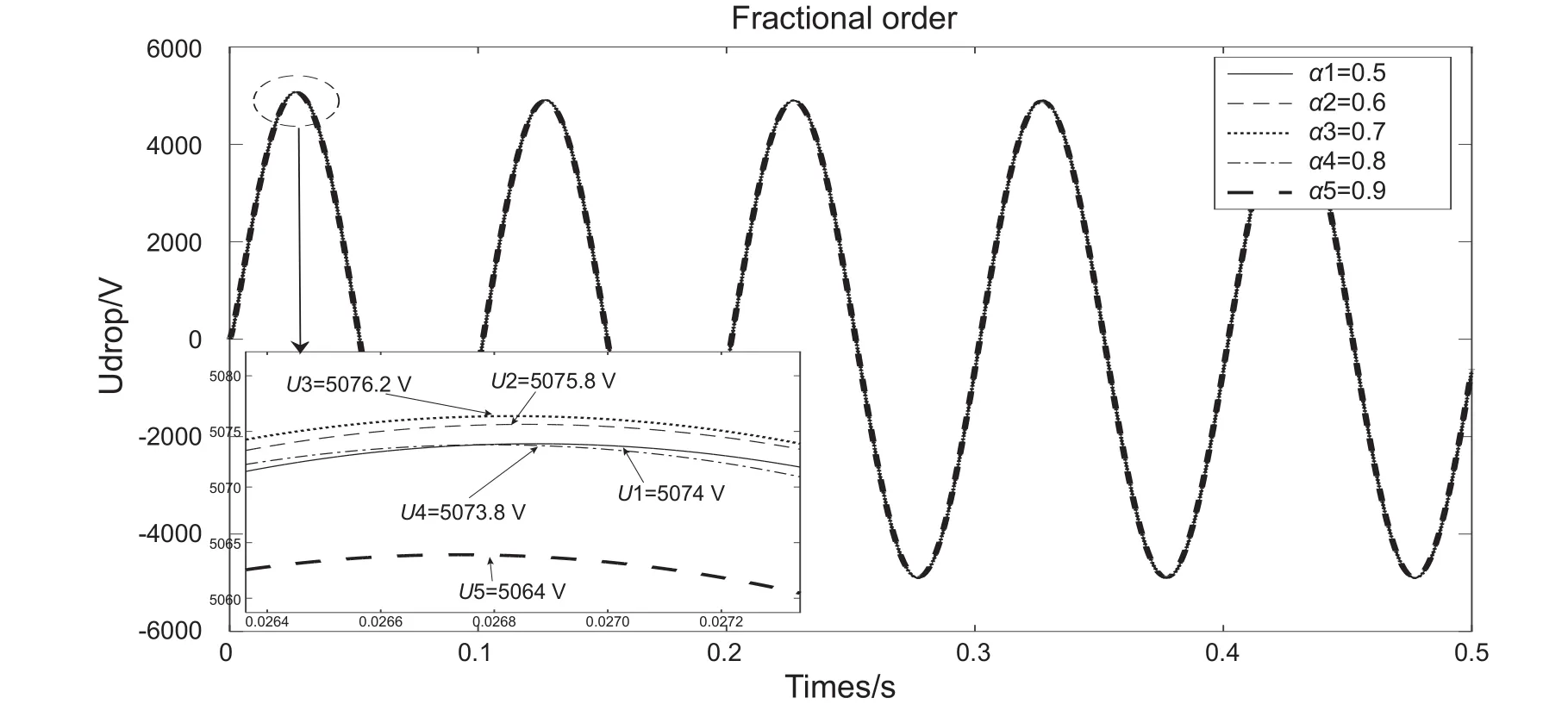
圖10 電纜分布電感分數階次對電壓降的影響Fig. 10 The effect of load cable distribution inductance fractional order on voltage drop

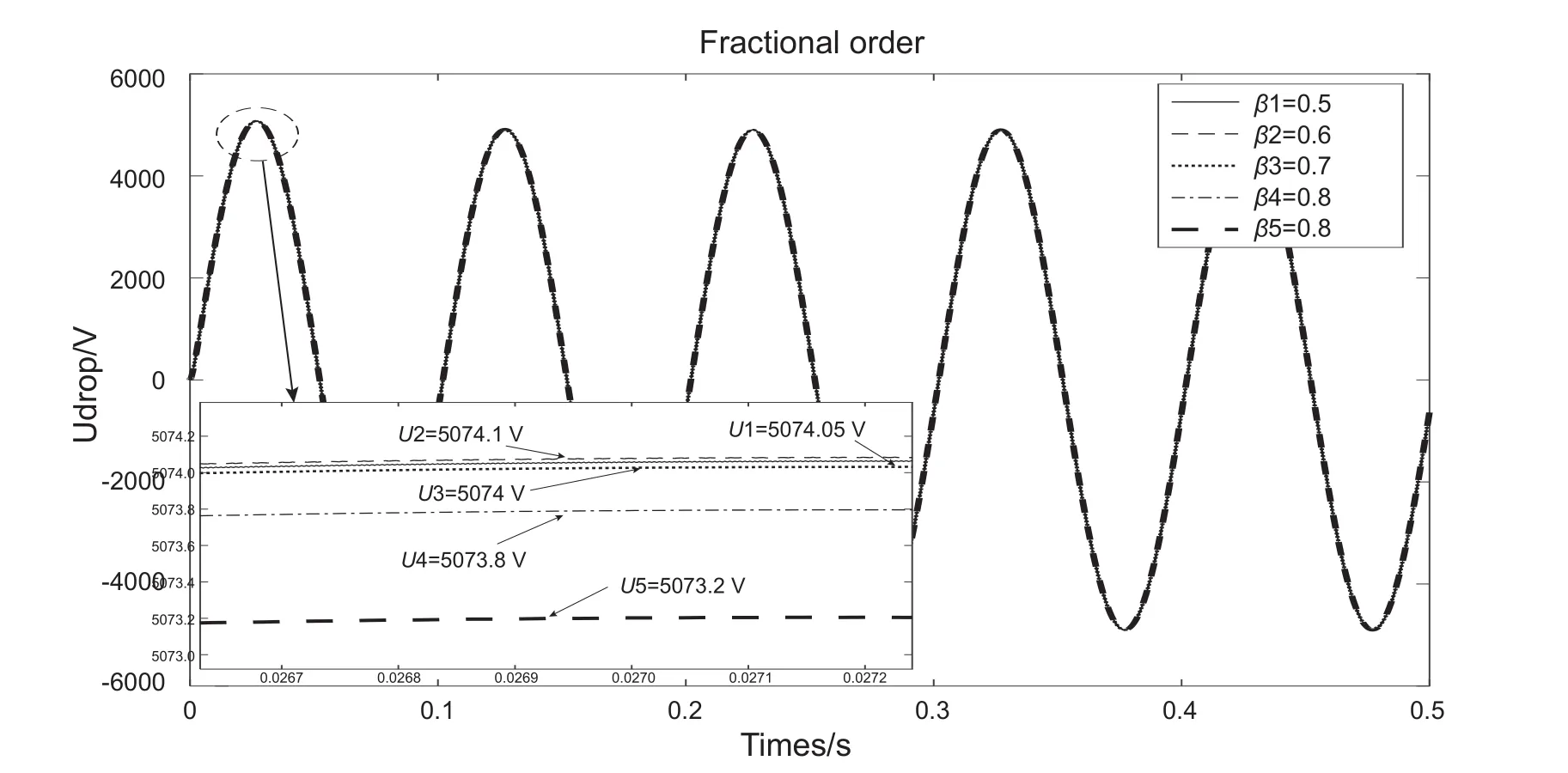
圖11 長電纜電壓降與電纜分布電容分數階階次的關系Fig. 11 The relationship between the voltage drop of long cable and the order order of the distributed capacitance of the cable

表2 電潛泵起動電壓降的變化規律Table 2 Change rule of electric submersible pump starting voltage drop

表3 電潛泵起動電壓降與電纜長度的關系Table 3 Relationship between starting voltage drop of ESP and cable length

3 結論

(1)基于Caputo-Fabrizio分數階微積分建立了變頻器—長電纜—電潛泵系統分數階模型，厘定了分數階與整數階量化比較標準平臺，比傳統模型能更加準確地描述深海長電纜電力傳輸特性。

(2)研究了起動電壓頻率、電纜長度、電纜分布電阻、電纜分布電感、電纜分布電容參數、負載特性阻抗和分數階階次等因素對電潛泵起動電壓降的影響。發現電纜分布電感參數對電纜電壓降的反常影響。

(3)分數階模型與整數階模型的計算結果相對偏差絕對值變化范圍是0.10%～30.35%，特別是當電纜長度和電纜分布電阻參數變化時，模型的相對偏差絕對值呈先減后增的V形分段。升壓變壓器補償電壓需要比傳統設計的高三分之一。基于分數階模型分析了起動電壓降，認為在實際應用中電潛泵變頻驅動電纜可以超過40 km。