滾筒殺青機系統的控制算法改進研究*
應文淵,趙章風,鐘 江
(浙江工業大學 機械工程學院,浙江 杭州 310014)
0 引 言
作為綠茶制作工藝中最重要的一步[1],殺青效果直接影響綠茶品質。現有的殺青設備中[2],電熱式滾筒殺青機因其加熱均勻、能源潔凈、價格較低、生產效率高,在茶葉加工生產中得到廣泛使用。滾筒殺青機的現場控制通過PID控制器控制筒壁溫度配合傳動及相關輔助設備完成殺青作業。該類殺青控制系統的問題有:(1)PID控制器的控制能力極大依賴于比例、微分、積分參數的設置,現有的經驗法Z-N整定和試湊法的參數取值難以保證PID控制的高有效性,致使殺青機的控制算法存在較大的超調量和波動量;(2)由于殺青溫度設置極為依賴人本身的經驗,而殺青過程中投葉速率和茶葉含水率會有所變化,其可靠性有限,導致殺青后常伴有一定量的焦葉黃葉現象(壞葉)。
滾筒殺青系統是非線性系統。對于非線性非理想的溫度控制系統,趙陽等人[3]基于變論域的模糊控制算法,實踐中收到了較為良好的控制效果;針對變速恒頻雙饋發電并網系統,呂艷玲、馮曦等人[4]將傳統PID控制與BP神經網絡控制相結合,提出了一種BP神經網絡PID的空載并網控制策略,該策略動態響應快、并網過渡過程短、穩態精度高、全局魯棒性高。
基于模糊算法和BP神經網絡PID的特性,本研究將引入模糊算法替代人工經驗,根據相關輸入條件確定對應溫度的精確值,并基于BP神經網絡的可自調整參數的PID控制器取代傳統PID控制器,通過改進滾筒殺青機控制系統算法,以優化殺青控制過程,避免或減少黃葉焦葉產生。
1 控制總體方案設計
1.1 滾筒殺青機的設備和殺青流程
本文中選用的殺青滾筒機型號為6CST50,實物圖如圖1所示[5]。

圖1 6CST50型滾筒殺青機
該系統主要由計量裝置、輸送裝置、傳動機構、滾筒、加熱裝置、排濕裝置以及相關由電器控制元件組成的控制箱等構成。整個工作過程傳統模式為先由計量裝置上的重量傳感器測定待殺青葉單批次投入質量M,經由經驗判斷所需的溫度后,對自帶的控制器輸入目標溫度以控制加熱電熱管開關占空比進行溫度控制[6],期間以溫度傳感器溫度作為反饋的傳統PID算法進行演算控制。
1.2 滾筒殺青機改進算法的控制方案
本文提出以模糊算法取代人工經驗求解對應多輸入的精確輸出值(溫度參數),并由BP-PID控制器取代PID控制器對溫度參數進行控制。控制方案分為兩部分:
(1)模糊決策部分[7]。輸入參數基于模糊算法計算對應控制參數具體值,為下一步控制器提供控制對象的精確目標值,對應輸出的滾筒筒壁溫度參數,本研究中選擇投葉速率(投葉量與傳輸時間決定)與茶葉含水率等級作為模糊算法推理的輸入條件[8],含水率等級由人工按不同茶葉工藝要求手動輸入[9],對控制器而言主要的參數即為滾筒筒壁溫度,因而將筒壁溫度作為模糊算法的輸出;
(2)溫度控制部分[10]。具有自整定功能的基于BP神經網絡的PID控制器[11-12],在PID參數最優化條件下,使筒壁溫度維持低誤差的動態平衡狀態,并針對變化快速反應調整。控制方案在基于MCU的嵌入式控制器上實現。
控制方案流程圖如圖2所示。
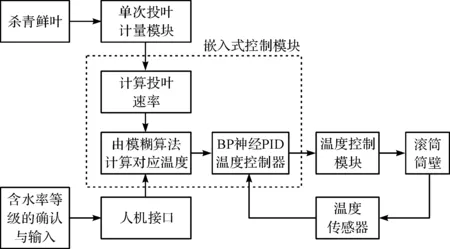
圖2 控制方案流程圖
2 控制模塊設計
控制模塊設計分為模糊算法設計和BP神經網絡控制器設計。
2.1 滾筒殺青機模糊推理模塊設計
在殺青作業中,參數間的相關性處于非線性關聯,對于這類不確定性系統,模糊算法由于利用語言信息,不依賴精確數學模型,可實現對不確定性系統的較好控制。因為本文引入模糊算法進行控制參數推理,模糊推理控制模塊以輸入殺青茶葉鮮葉的含水率等級和茶葉投葉速率兩個參數為基準,通過模糊算法推斷出符合殺青工藝的滾筒壁溫度,最后輸入到PID控制器(注:不同類型的茶葉有著各自殺青工藝要求[13],其對應的模糊推理有所不同)。本文僅針對二芽一葉的葉片進行研究。
2.1.1 隸屬度函數建立
筆者選擇Matlab的Fuzzy工具箱構建基于各輸入(出)參數對應的單輸出模糊算法模型。考慮到控制系統的魯棒性和靈敏度,選擇三角函數來進行構建對含水率等級、投葉速率、筒壁溫度的隸屬度函數。
首先本研究將待殺青鮮葉含水率進行分級,在這里分為5個等級,以此建立模糊子集{A,B,C,D,E},依次表示為:低含水率,較低,中度,較高,高含水率。結合該類茶葉殺青工藝的實際經驗,設定論域范圍:[20,90]。含水率具體隸屬度函數如圖3所示。
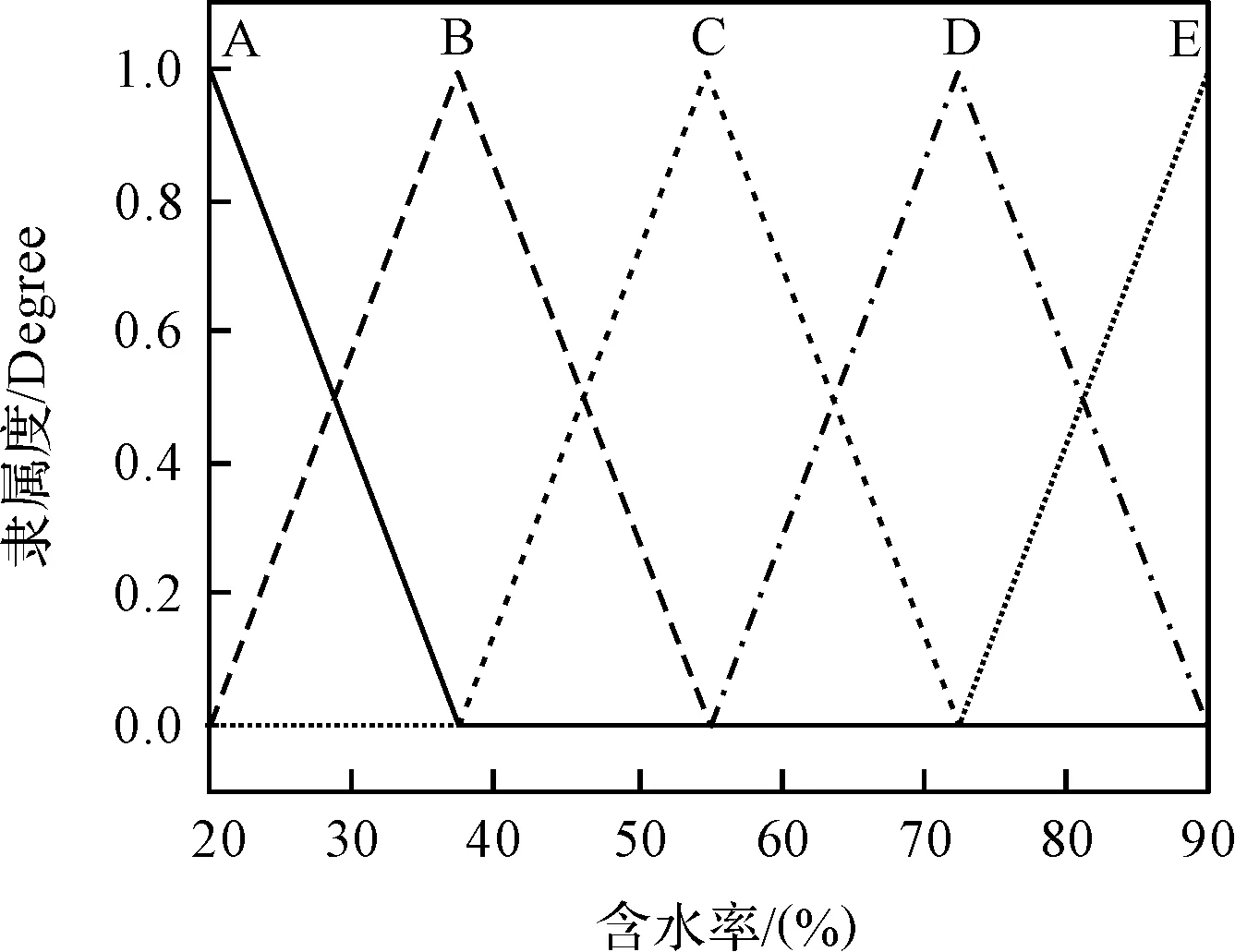
圖3 含水率隸屬度函數
根據理論推算與經驗,6CST50殺青機的投葉速率應在0.5 kg/min~2.0 kg/min之間,故論域范圍為[0.5,2.0]。本研究將投料速率也分5個等級,建立投葉速率模糊子集為{S MS M MB B},依次代表慢速,稍慢,中速,稍快,快速。
投葉速率具體隸屬度函數如圖4所示。
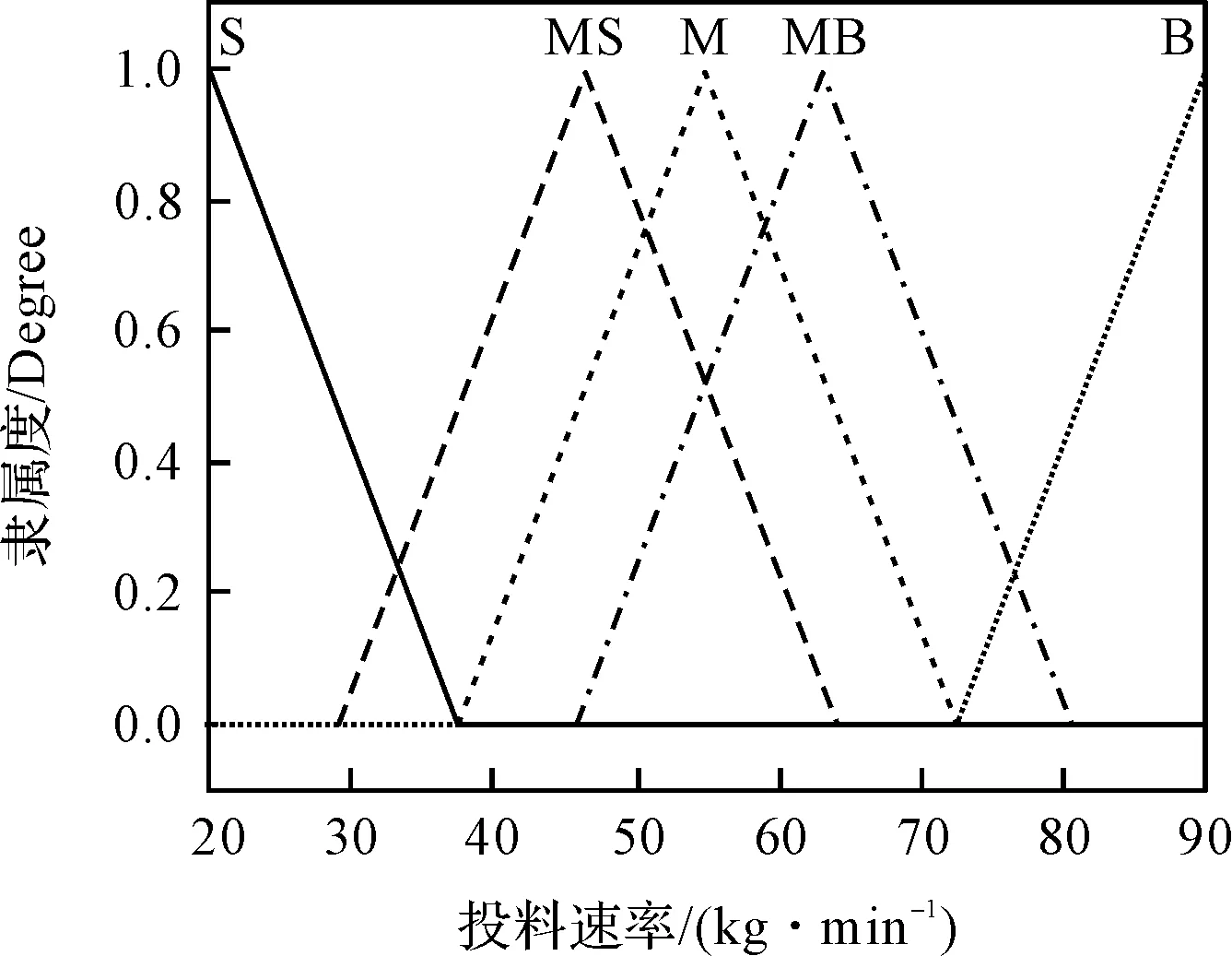
圖4 投葉速率隸屬度函數
在茶葉殺青的過程中,不僅要求短時間內達到高溫,令茶葉內多酚氧化酶失活[14],也要避免過高溫度使得茶葉燒焦。根據專家經驗,符合要求的滾筒溫度取值在110 ℃~160 ℃,確定論域設置為[110,160].建立模糊子集{L ML M MH H},依次代表溫度程度:低溫、中低溫、中溫、中高溫、高溫。滾筒筒壁溫度具體隸屬度函數如圖5所示。
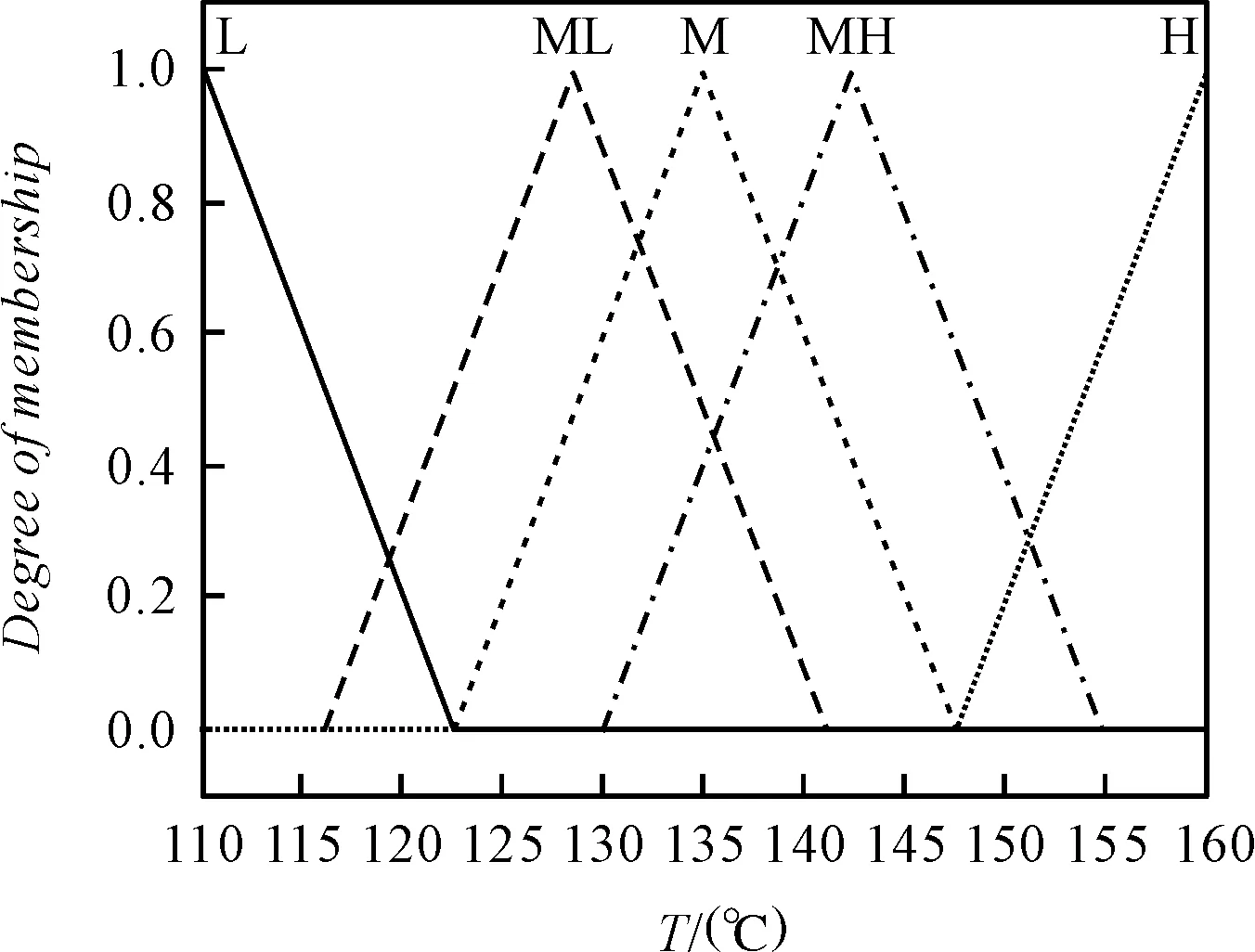
圖5 滾筒筒壁隸屬度函數
2.1.2 模糊規則建立
本研究根據滾筒殺青的經驗建立模糊推理的規則表,如表1所示。

表1 滾筒溫度模糊規則表
2.1.3 模糊推理
模糊規則類型:IF AND THEN。由此,推理結論為:
U′=(X×Y)°R
(1)
式中:X,Y—含水率和投葉速率的模糊集;R—由上表得的模糊蘊含關系;U′—輸出模糊集。
全部控制規則對應的總規則為各規則取“并”操作合成:
(2)
式中:Ri—基于表1的各條模糊關系。
2.1.4 模糊決策
為得出對應的目標溫度,算法最后應輸出確定值而非模糊輸出值,故而需對模糊輸出值進行解模糊,使得到確定值,這一過程稱作模糊決策。在本研究中采用加權平均解模糊法。其公式如下:
(3)
式中:Ui—模糊集U中的元素;μ(Ui)—Ui對應的隸屬度;u—加權平均后的輸出結果。
最終由fuzzy工具箱得到基于投料速率和含水率的滾筒溫度輸出效果圖,如圖6所示。
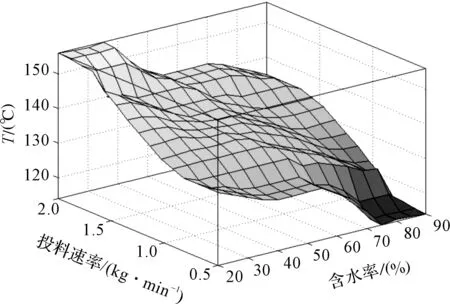
圖6 滾筒溫度輸出效果圖
根據該模糊算法模型,可根據輸入得出殺青所需溫度的具體值,實現投葉速率和含水率變化下的溫度目標參數動態調節。該算法上可有效降低純依賴經驗的不可靠性。
2.2 基于BP神經網絡的PID控制器設計
PID控制效果的好壞,取決于比例、積分、微分3個控制參數的取值和共同作用[15]。BP神經網絡善于處理機制復雜的非線性映射,并具有高度自學習自適應能力,故本研究將BP神經網絡與PID算法結合,以自適應地為系統選擇出優化的PID控制參數。
2.2.1 控制器的總體設計
基于BP神經網絡的PID控制器有兩部分組成:BP神經網絡部分和PID控制器。PID控制器部分利用輸入rin與輸出yout的誤差e、誤差變化de/dt、以及由BP神經網絡在線調整的Kp、Ki、Kd參數,由控制算法得出控制器輸出u(k),再通過控制對象Plant的傳遞函數得到系統輸出yout以實現被控對象的閉環控制。而BP神經網絡部分根據最優化的性能指標監督下,通過BP神經網絡的自學習過程和權值自調整,使該部分輸出對應最優控制指標或近似最優PID控制器參數Kp、Ki、Kd。控制器的具體結構圖如圖7所示。

圖7 基于BP神經網絡的PID控制器結構框圖
2.2.2PID算法的選擇
本文選擇增量式數字PID作為PID算法的表現形式。增量式數字PID控制因通過求出增量,將原先PID的積分環節的累積作用進行了替換,避免積分環節占用大量計算性能和存儲空間。算法具體表示如下:
u(k)=Kp(e(k)-e(k-1))+Kie(k)+
Kd(e(k)-2e(k-1)+e(k-2))
(4)
為保證計算實時性與效率,本文選用3層的BP神經網絡(輸入層、隱含層和輸出層)。各層輸入輸出和非線性激勵函數表示如下:
(1)網絡輸入層的輸入:
(5)
式中:M—輸入變量個數。
(2)網絡隱含層的輸入、輸出為:
(6)
(7)
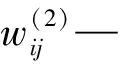
隱層神經元的非線性激勵函數為正負對稱的Sigmoid函數,即:
(8)
(3)網絡輸出層的輸入輸出為:
(9)
輸出層對應節點分別對應3個可調整參數Kp、Ki、Kd。因為PID的參數不能為負,故輸出層的非線性激勵函數設為非負的Sigmiod函數,即:
1.2.2 排除標準 排除入組時根據病史采集情況,已經患有冠心病、心絞痛、心肌梗死、腦出血,腦梗死,腦栓塞的人群。
(10)
對輸出層權值的學習算法為:
(11)
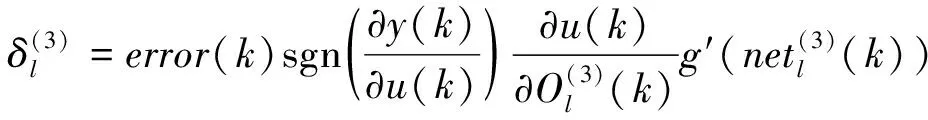
(12)
隱含層的權系數學習算法同理有:
(13)
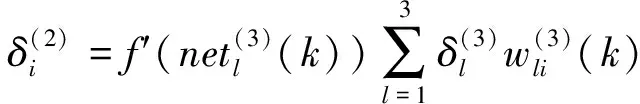
(14)
式中:g′(x)=g(x)(1-g(x));f′(x)=(1-f2′(x))/2;δ—神經元的誤差信號;η—學習速率;α—慣性系數。
以此BP神經網絡算法為基準,即可實現有自整定功能的PID控制器,以極大優化控制參數,并在傳遞性質發生變化的情況下,可自適應調整PID控制器的參數。
BP算法流程圖如圖8所示。

圖8 BP算法流程圖
BP-PID算法可以總結為:
(1)首先確定BP網絡的結構,即確定輸入層節點數和隱含層,并且給定網絡各層加權系數的初值,選定合適的學習速率η和合適的慣性系數α,此時k=1;
(2)通過采樣得到r(k)和y(k),計算該時刻誤差e(k)=r(k)-y(k);
(3)通過計算神經網絡各層神經元的輸入、輸出值,來確定其中神經網絡輸出層的輸出,對應PID控制器Kp、Ki、Kd這3個參數;
(4)計算PID控制器的控制輸出u(k),并將控制輸出u(k)參與系統進一步控制和計算;
(5)進入神經網絡的學習過程,并且實時調整各加權系數,最終在線自適應調整PID的控制參數;
(6)令k=k+1,再返回到步驟(2),一直到所得到的誤差滿足要求為止。
3 控制器的仿真和對比分析
本研究選用的BP神經網絡其結構為3層,其中輸入層4個神經元,輸出層3個神經元(各神經元依次輸出PID參數)。學習速率0.28,慣性系數0.05。各初始權值設為[-1,1]的隨機數。BP神經網絡PID的Simulink模型包括輸入模塊、控制模塊、被控對象模塊等部分。仿真的輸入信號為階躍信號。本研究對象的系統為一階慣性系統,故將滾筒殺青機系統的傳遞函數[16]設置為2.04e-9s/(80s+1),以湊數法獲得PID控制器的參數Kp=2.7,Ki=0.031,Kd=3。湊試法的原則為參考各參數對系統控制過程的影響趨勢,對參數調整實行先比例、后積分,再微分的整定步驟。具體模型如圖9所示。
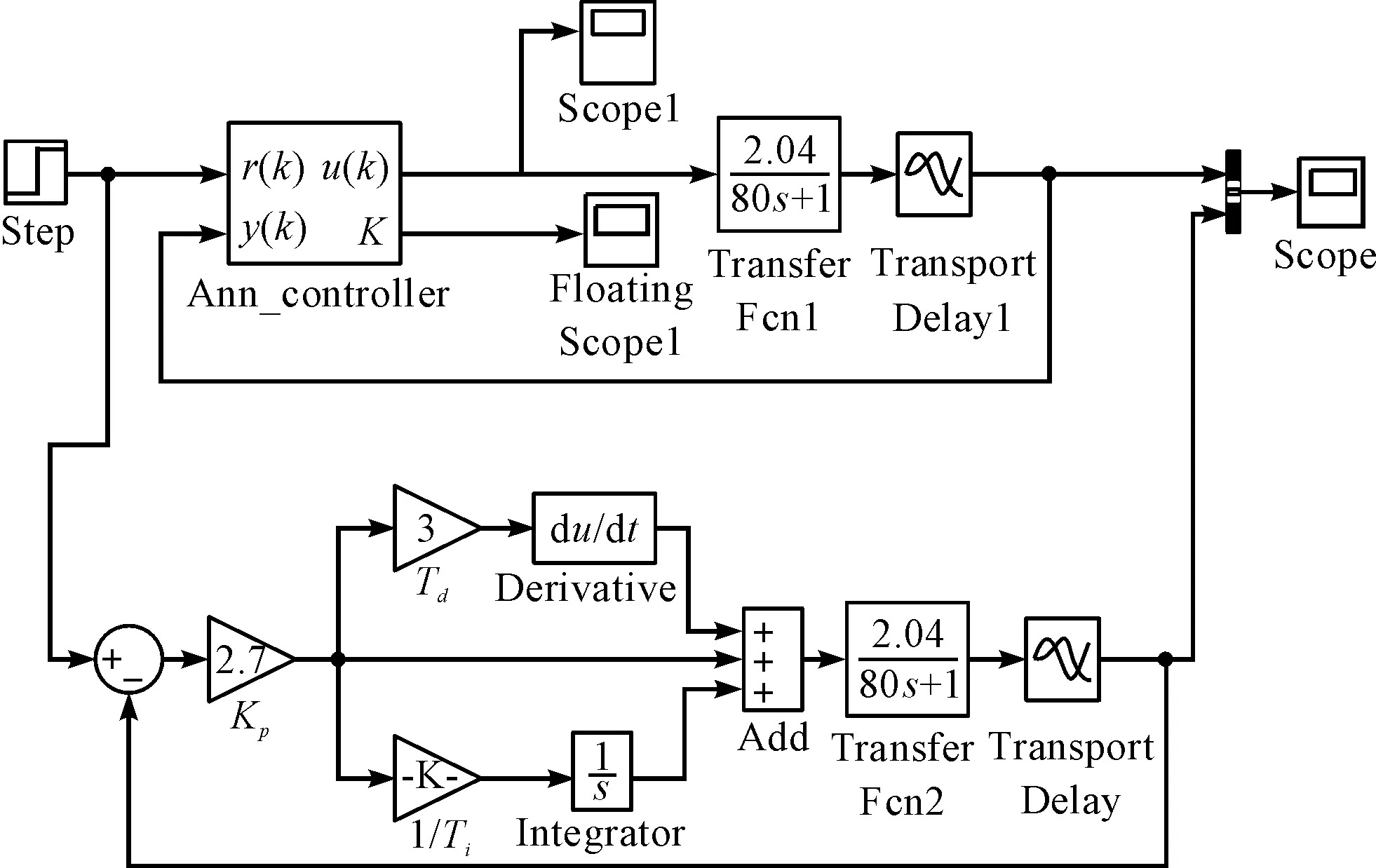
圖9 BP-PID仿真模型
圖9左端為輸入信號,用Step模塊(單位階躍);Ann_controller是一個控制模型的封裝,由一個基于S—function的子系統構成。控制模型的r(k)接輸入信號,y(k)接輸出反饋信號。u(k)為控制器輸出信號,K為神經網絡PID控制器的Kp、Ki、Kd輸出,輸出直接作用被控對象,神經網絡PID控制器封裝于Ann_controller模型中,Ann_controller控制器的子系統如圖10所示。
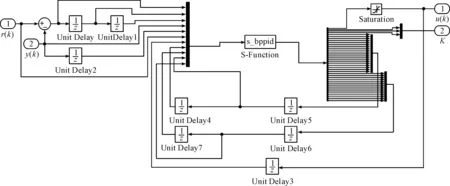
圖10 Ann_controller封裝內部結構
在圖10中,左端口1(r(k))與左端口2(y(k))為系統輸入,相減后將誤差信號和誤差的導數信號輸入給控制器,右端口1(u(k))與右端口2(K)為系統輸出,延時模塊分別將神經網絡的各個權值反饋給控制模塊S—function。
本研究進行了仿真,得到的仿真結果如圖11所示。
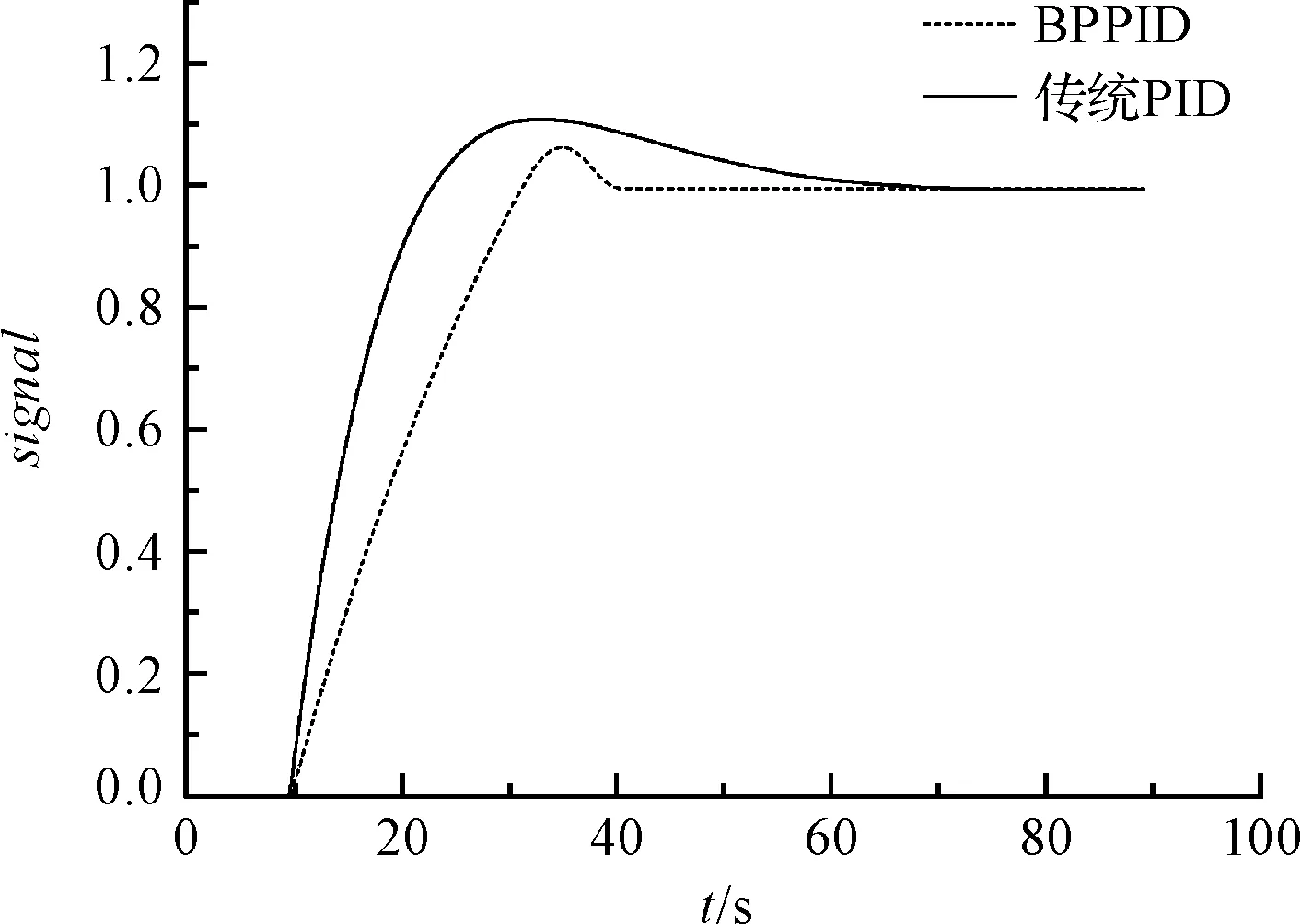
圖11 兩類算法結果對比
在圖11中可見:傳統PID算法超調量σ=11.1%,調節時間ts=67 s,穩態誤差es= 0;BP神經網絡PID算法自適應完成了對參數的調整,超調量σ= 6.7%,調節時間ts=45 s ,穩態誤差es= 0。由此可看出基于BP神經網絡的PID算法在超調量和調節時間等指標上都比傳統PID算法都具有更優的特點。
4 實驗驗證
本研究在衢州上洋機械6CST50型號滾筒殺青機上進行實驗,并由R232接口將溫度數據傳輸入PC端進行記錄。為驗證控制系統效果,進行對比試驗,組一基于改進后算法進行殺青控制作業,記為A組;組二基于傳統PID,記為B組。實驗條件如表2所示。
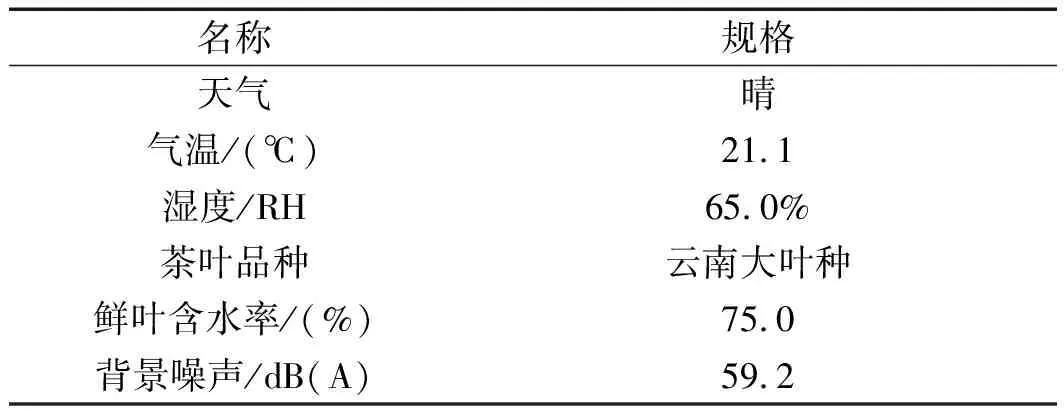
表2 實驗條件表
經實驗測得各組溫度曲線,實驗結果如圖(12,13)所示。
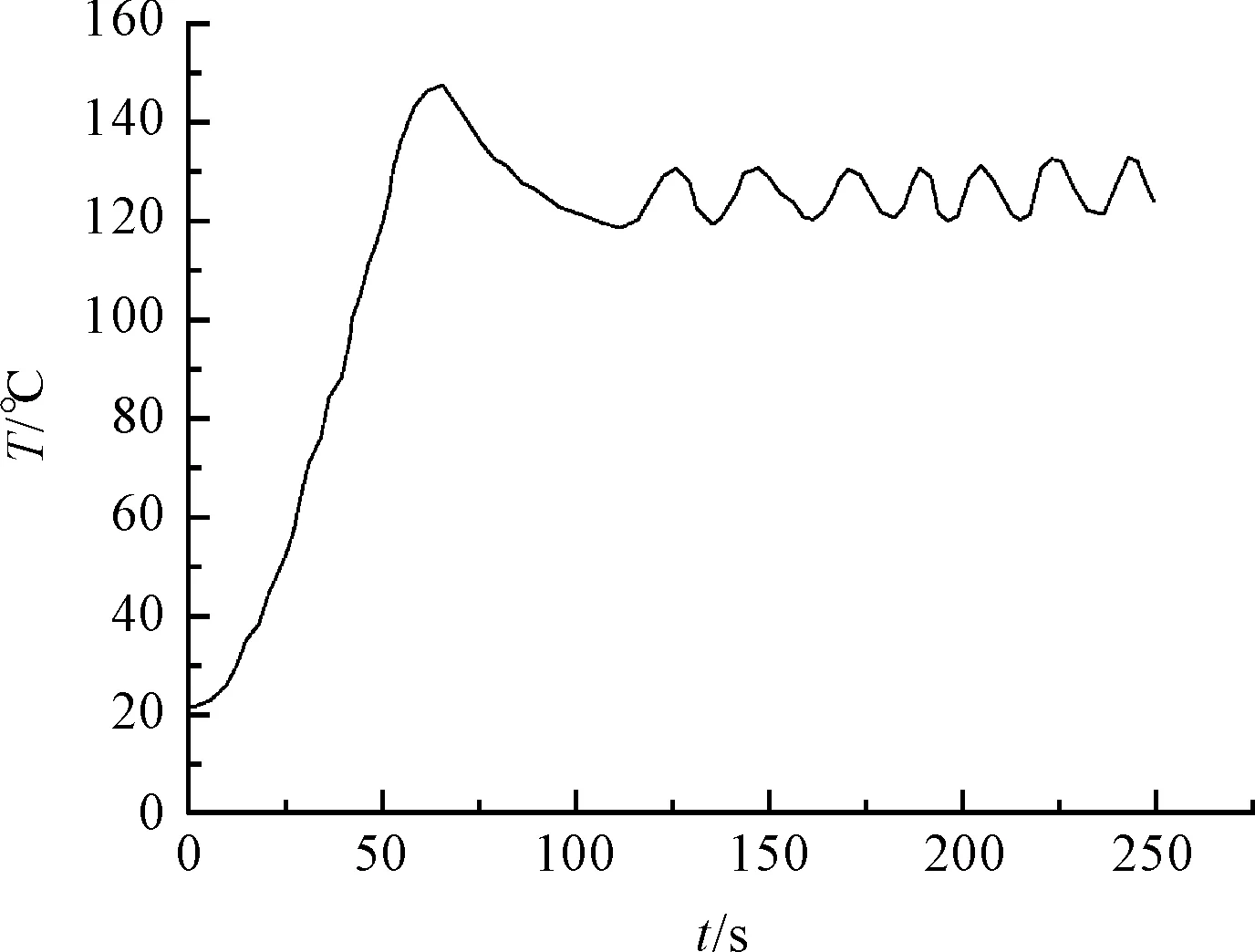
圖12 傳統PID算法實驗圖
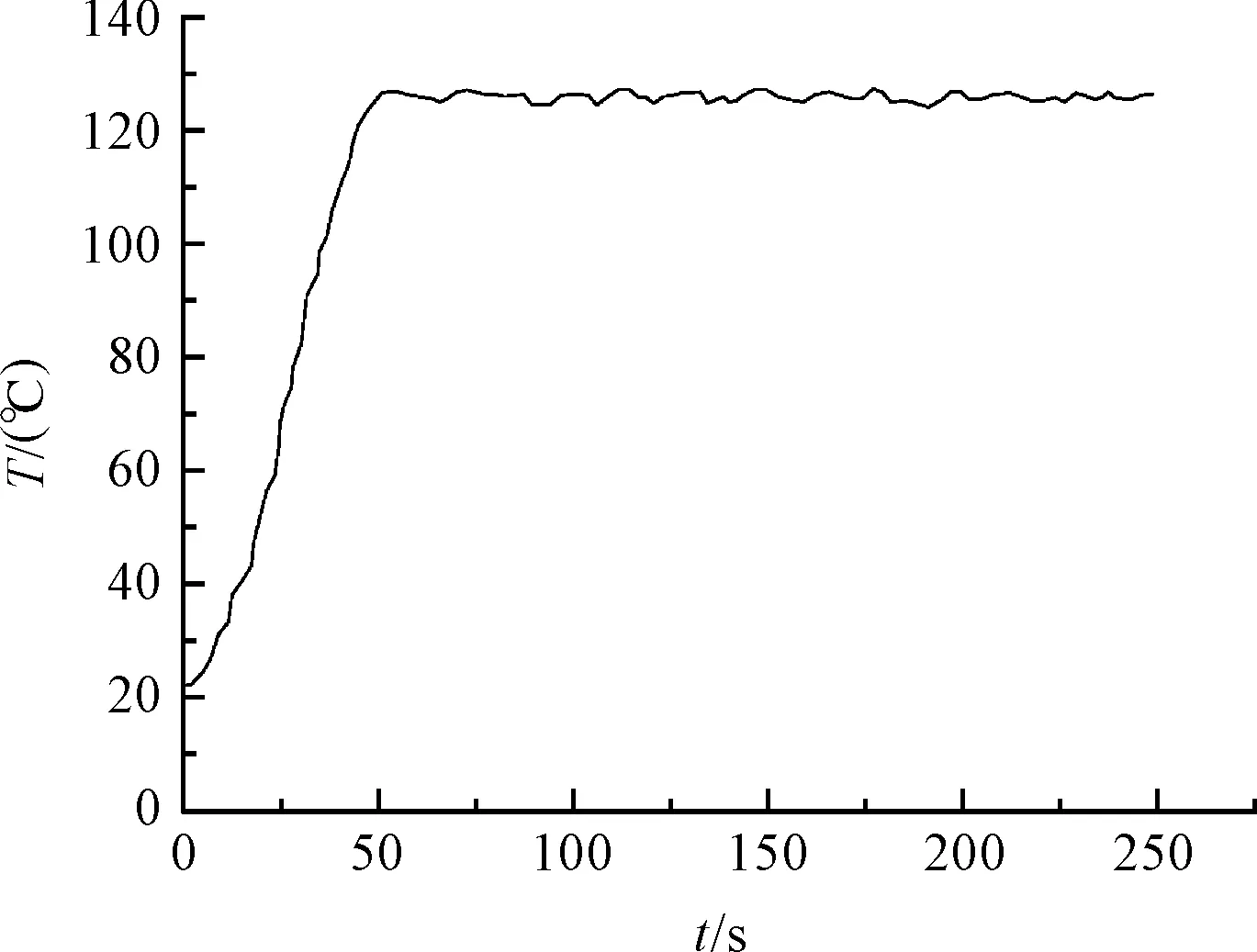
圖13 BP-PID算法實驗圖
經由圖(12,13)可知:BP-PID算法在超調量、調節時間和波動誤差上的表現都明顯優于傳統的PID算法。
根據技術指標對兩組茶葉殺青后質量進行綜合判定,結果如表3所示。
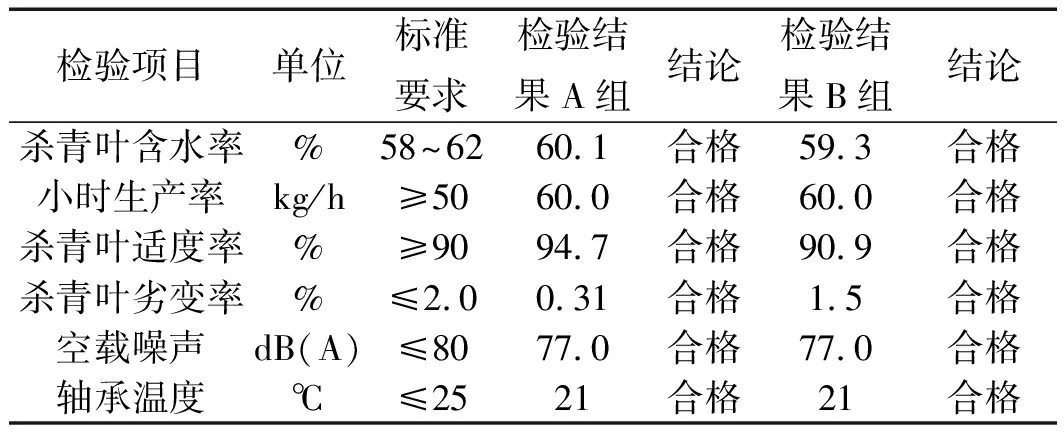
表3 實驗結果檢測報告
綜合表3及現場檢驗可知:A組茶葉色澤青綠,基本無焦葉焦邊;B組色澤相對較暗,存在一定程度葉有焦邊。得出結論:本文改進算法后的控制系統所生產的茶葉比原先傳統的PID恒溫控制算法生產的茶葉品質更好,物料損耗更少。
5 結束語
基于滾筒殺青工藝,本文以Matlab軟件進行模糊推理和BP神經網路PID控制器的系統仿真,并且基于以MCU的嵌入式系統、現場相關控制實驗驗證了改進算法的可行性和對殺青效果提升的有效性,得到以下結論:
(1)基于工藝和殺青經驗,可針對要求,根據輸入由模糊算法推導出可行的滾筒溫度,降低純依靠經驗的不可靠性和盲目性;
(2)相較于PID溫度控制系統,BP神經網絡PID對溫度的控制效果更好,且可以進行自適應調整;
(3)基于模糊算法和BPPID算法改進后的控制系統可以將整個加工過程更加精確化,模式化,提升作業效率和可控性。

