旋轉機械軸系裝配體位置公差預測方法與優化研究

閆清東， 陳修齊， 魏巍， 黃靜秋， 楊啟福

(1.北京理工大學 車輛傳動國家重點實驗室， 北京 100081；2.北京電動車輛協同創新中心， 北京 100081；3.江麓機電集團有限公司， 湖南 湘潭 411100)

0 引言

作為一種典型的旋轉機械，液力變矩器裝配體從定位基準導輪軸端面到裝配體末端供油套之間，供油套的徑向圓跳動作為液力變矩器末環裝配誤差，是檢驗液力變矩器各零件綜合公差水平和整體加工水平的重要檢驗標準。

一旦徑向圓跳動出現不滿足設計要求的超差現象，會導致對供油套起密封作用的密封環發生磨損，嚴重時會導致供油套功能失效，從而造成液力變矩器閉鎖油泄漏，進而影響液力元件性能，使得整車驅動系統失效。而對某液力變矩器而言，盡管組成環各零件均滿足設計公差要求，但其裝配體累積到末端的徑向圓跳動卻時有超差現象發生，其原因在于位置公差傳遞缺乏準確的理論分析指導，對應軸系各零件公差耦合傳遞機制不清晰。

為對裝配體公差帶進行準確預測和描述，研究人員構建了一系列理論模型：Requicha[1]提出以變動簇為基礎的實體漂移法，通過以保持實體外形不變的拓撲變換，經漂移形成的漂移帶即為公差帶。在此基礎上，張文祖等[2]完善了實體漂移理論，提出了漂移模型。Hillyard等[3]提出參數矢量化方法：將幾何實體視作參數化幾何框架，利用矢量位移表征公差大小；將尺寸信息作為固件框架，將尺寸公差視作在固件框架基礎上允許的微小變動。Hoffmann[4]從三維歐式空間角度對公差帶進行定義，將以點矢量為參數的公差函數施加上下界條件約束，表達為公差函數的形式。劉玉生[5]提出了基于自由度變動的公差平面數學表示方法，研究不同類平面的尺寸公差約束形式，廣義地推導了尺寸公差數學模型。蔡敏[6]建立了圓柱要素形位公差的數學模型，將圖形與文字定義的公差嚴格表征為矢量方程的形式。黃德智[7]借助計算機輔助工具，在虛擬環境下實現裝配體公差的三維標注，并采用了基于Halton序列的擬蒙特卡洛公差分析法，引入裝配成功率等概念對公差設計結果進行評價。孟祥海等[8]運用二維裝配偏差建模和三維尺寸鏈建模相結合的方法，分析了裝配體支點同心度的影響因素。

以上模型多數討論和分析了單個零件的公差綜合，在面對有多個配合面、多個約束條件的旋轉機械時，其公差理論模型的建立較為復雜，對應其公差的傳遞機制不清晰，難以對其形位公差累積進行有效的理論預測。

為此，本文提出一種預測累計到裝配鏈末端徑向圓跳動值的變動邊界圓法，預測徑向圓跳動公差范圍，并通過蒙特卡洛公差分析全局優化方法，根據所提出的公差傳遞模型對公差設計進行優化。

1 基本假設與問題描述

1.1 基本假設

在描述旋轉機械軸系裝配體徑向圓跳動位置公差傳遞機制之前，先提出下列假設：

1)本模型分析裝配體徑向圓跳動位置公差傳遞機制，將各環零件視為剛體。不考慮零件在力、熱或環境影響下的變形。

2)本文對誤差的計算處理基于蒙特卡洛公差分析法,認為各零件(組成環)的實際尺寸均符合正態分布規律。

1.2 問題描述

某型液力變矩器的供油套徑向圓跳動值[9]定義為：裝配體末端供油套繞導輪軸端面軸線(見圖1)轉動時,徑向測得的最大讀數與最小讀數之差。

但實測中大量樣本出現難以滿足設計值Δ=0.25 mm的現象(Δ>0.3 mm)，為能滿足設計要求，本文擬從累積精度角度解釋優化的原理，并分析徑向圓跳動形位公差裝配體傳遞機制。分析對象為某液力變矩器供油套的徑向圓跳動，其徑向圓跳動主要受其零件加工精度和裝配累積精度兩方面的影響。其裝配累積精度影響因素為： 1)軸線對基準軸線的同軸度誤差；2)圓柱面的圓柱度誤差；3)各零件軸線相對于基準軸線的偏角累積公差。

2 模型建立

2.1 整體模型

變動邊界圓定義如下：在求徑向圓跳動值過程中，若只考慮回轉體零件旋轉時與基準軸線的最大距離與最小距離，可將其視為半徑為ρ的圓繞某點(偏心距為e)回轉。其最遠距離用ρ+e表示，最近距離用ρ-e表示。

將徑向圓跳動公差簡化為只與距回轉中心最大距離和最小距離有關，因此旋轉面的模型可以視為圓柱體模型。以基準軸線為z軸，建立如圖2所示的柱體模型。

如圖2所示的實際軸線無傾角模型所示，供油套零件繞基準軸線旋轉，如果其端面與基準軸線的最遠端距離為ρ1max、最近端距離為ρ1min，則其徑向圓跳動公差可表示為

d1=ρ1max-ρ1min=2e.

(1)

但在工程實際中，還要考慮零件實際軸線相對于基準軸線的傾角θ(見圖3)，此時端面與基準軸線的最遠端距離為ρ2max，最近端距離為ρ2min.

徑向圓跳動公差可通過圓柱模型上的幾何關系(2)式、(3)式進行計算：

(2)

(3)

故

(4)

(2)式～(4)式中，α與θ互余，在ρ確定的情況下，可由零件高度確定。ρ與e為水平面參數，可通過2.2節中的模型計算求出。

2.2 水平面參數傳遞模型

利用水平面參數ρ和e可以表征裝配環末端在其余i個裝配環約束下的最大邊界及其軸線相對于基準軸線的同心度。根據參數ρ和e表示出的零件繞軸線轉動極限距離ρmax與ρmin，可以得到徑向圓跳動值。

裝配環的累積精度受各個裝配環平面參數的影響，可以用函數形式表示出第i個裝配環水平參數對裝配環末端的作用：

F(ρ,e)=f1(ρ1,e1,…,ρi,ei)+
f2(ρ2,e2,…,ρi-1,ei-1)，

(5)

式中：f1與f2分別為兩種作用類型不同的組成環與裝配環末端的函數關系。

2.2.1 第1類組成環作用機理

在同軸度作用下，位置誤差的傳遞過程可用一端的水平參數(ρA，eA)與另一端水平參數(ρB，eB)的關系來表示。

以A面、B面表示在同一個回轉體零件的上下端面(見圖4)，B端面相對于A端面同軸度公差值[9]為T，可以轉化為名義尺寸為0，公差為0.5T的線性尺寸0±0.5T的偏心距e′.

設A面水平參數ρA=ρ，eA=e，若不存在同軸度誤差，則B面水平參數應與A面相同，即ρB=ρ，eB=e，徑向圓跳動d=2e.

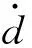
2.2.2 第2類組成環作用機理

在軸孔配合作用下，位置誤差的傳遞過程可用軸截面水平參數(ρB，eB)與孔截面水平參數(ρA，eA)的關系來表征。

設孔截面水平參數ρA=ρ，eA=e，若軸孔配合絕對平滑，不存在誤差，則軸截面的水平參數應與孔截面相同，即ρB=ρ，eB=e，徑向圓跳動d=2e.

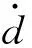
由此，可將所有裝配環的約束按影響類型歸為第1類裝配環或第2類裝配環，復雜裝配體的累積精度可以簡化為以上兩種基本函數各自的累加和。

2.3 傾角參數傳遞模型

回轉體零件裝配方式為定心安裝，但由于加工表面存在著一定的端面圓跳動，在裝配過程中會產生傾角的累加。其傳遞機制與水平參數基本相同，受單參數θ影響。類似地，其裝配環末端在其余i個裝配環Ai約束下的傾角累積程度可用函數形式表征。其傳遞模型示意圖如圖5所示。

F(θ)=f(θ1,θ2，…，θi).

(6)

3 模型計算

以某型液力變矩器為計算實例，建立傳遞函數模型，計算其平面參數，按照在傳遞過程中對裝配環末端的作用結果將裝配環分為第1類裝配環和第2類裝配環兩類，其極限狀態表達式以及對誤差傳遞的作用形式見第2節。

根據液力變矩器裝配關系和各零件間的軸孔配合形式，建立液力變矩器的嵌套模型，某型液力變矩器配合面如圖6所示。根據此模型可以表征出同一零件的上下兩個端面特征和各零件配合面之間存在的軸孔間隙。

3.1 模型分析

從圖6的模型可以直觀看出，在同軸度作用下，同一零件前后端面變動邊界圓的偏心距e改變，而變動邊界圓的半徑ρ不變。而在軸孔配合中，分屬相鄰兩個零件上同一端面的前后側變動邊界線圓的半徑ρ改變，而變動邊界圓的偏心距e不變。

在第1類組成環(相關參數見表1)作用下，變動邊界圓偏心距e發生改變，而變動邊界圓半徑ρ保持不變。下面列出模型中第1類裝配環相關參數。這里引入尺寸鏈傳遞系數Ci[9]，Ci表征各組組成環對封閉環的影響。當Ci>0時該環為增環，當Ci<0時該環為減環。

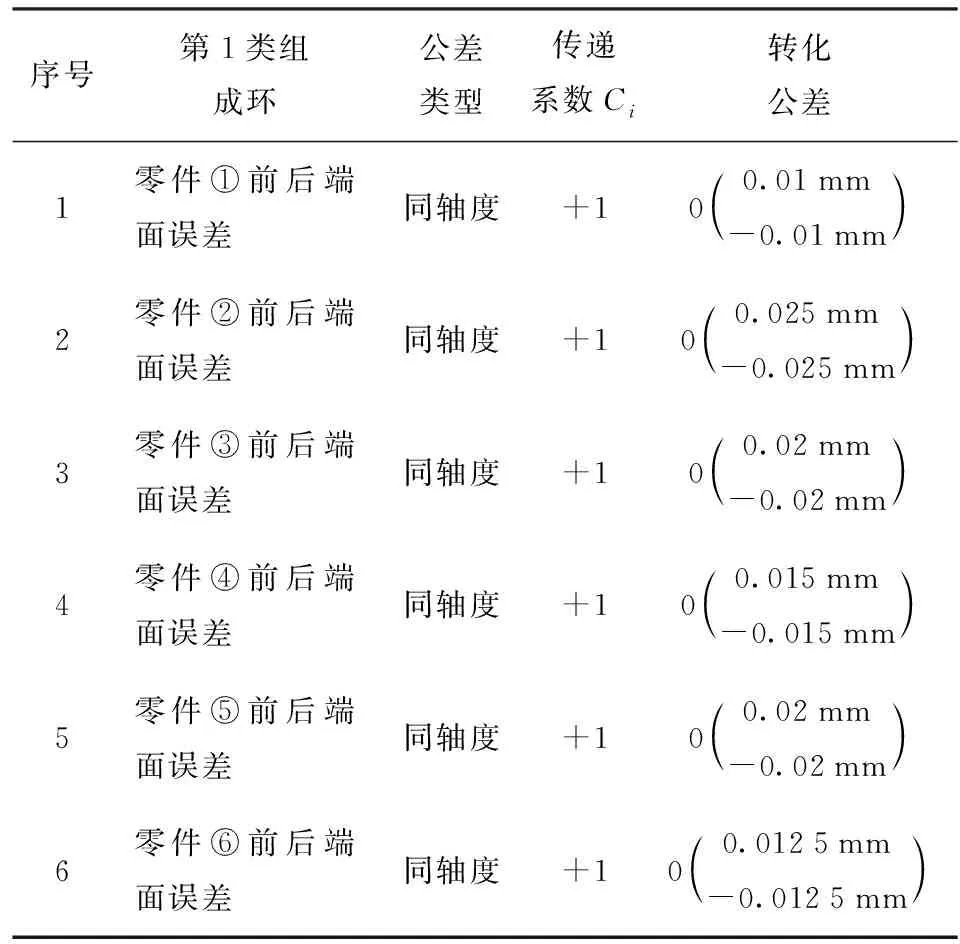
表1 第1類裝配環相關參數

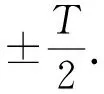
(7)

式中：k0為封閉環相對分布系數；n為裝配環個數。

封閉環公差帶中心μ0為

(8)

式中：μi為各環組成環公差帶中心。

依據本文模型，第1類裝配環個數n=6，則第1類環累計公差帶寬Te為

(9)

下面列出第2類裝配環參數(見表2)。第2類裝配環影響變動邊界圓的半徑，而變動邊界圓偏心距保持不變。

表2 第2類裝配環相關參數

第2類環累計公差帶寬為

(10)

利用此模型和第2節中建立在此模型基礎上的計算方法，對液力變矩器末端的徑向圓跳動變動邊界線圓的參數(ρ，e)進行計算，得到其水平變動邊界圓參數為

ρ1max=μρ+μe.

(11)

下面考慮次要影響因素，工程中傾斜誤差較小，傾斜角可用其正切值表示。令回轉體零件第i環的端面圓跳動為hi，第i環的直徑為Di，則該零件端面的正切值分別為

(12)

令各裝配環傾角值tanθi變化范圍為Tθi，則裝配環末端傾角值tanθ0變化范圍Tθ0可表示為

(13)

根據(4)式即可求出裝配末環累積公差變動范圍。

3.2 蒙特卡洛法模擬計算

機械產品在大批量加工時，在加工過程穩定、影響因素眾多且相互獨立的情況下，零件尺寸變動將符合正態分布。基于這種裝配特性，可以采用蒙特卡洛法[10]模擬組成環實測尺寸值，對裝配環的累積精度進行計算。

依據蒙特卡洛法，抽取符合各裝配環參數的各環誤差樣本2 000組，分別為{εj1，εj2，εj3，…，εj9}(其中j為樣本容量，εj1到εj9對應第j組子樣本的裝配環誤差)，計算流程如圖7所示。

依據蒙特卡洛法模擬計算流程，得到2 000次蒙特卡洛抽樣下的樣本邊界圓范圍擬合曲線(見圖8)。

由高斯曲線擬合結果可知，水平邊界圓參數e=0.032 5,ρ=0.124.

將水平邊界圓范圍代入第2節模型中，得到徑向圓跳動均值為0.328 mm，分布范圍在0.299～0.355 mm之間。與實測產品精度范圍(見圖9)相符合，遠遠超出設計要求0.25 mm.

4 優化設計

當前方案下，徑向圓跳動值無法達到產品目標精度要求，現以平均裝配精度和加工成本為目標進行聯合優化設計。借助遺傳算法[11]，優化變量為各裝配環尺寸公差的精度等級。

4.1 優化目標參數及適應度表達

首先定義優化模型中的平均裝配精度和加工成本，并建立精度優化目標函數關系。其中：

零件加工成本可視為設計公差值T的函數，本裝配體加工成本的計算依據我國中型機械類企業在中等批量加工時，各種特征尺寸加工成本的先驗公式[12]，代入裝配環各零部件的外圓及內孔特征、平面尺寸、形狀特征及裝配可靠度。結合各裝配環具體公差等級，得到加工成本。

在這兩項目標優化中，每組方案的裝配累積精度的平均裝配精度可以通過蒙特卡洛法進行模擬計算，加工成本C(T)可以通過每個裝配環公差T求得。

灰色關聯度[13]常用于分析系統動態發展趨勢，根據灰色關聯法建立適應度函數,用灰色關聯度系數表征當前方案與最優方案的關聯程度，作為遺傳算法的適應度。灰色關聯度的歸一變換及關聯度向量表達方式見文獻[13]。

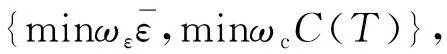
式中：ωε、ωc為設計人員依據當前產品的生產和使用指標所得到的權重系數；Ti為各個裝配環的公差等級；Tc為裝配體累積精度，需滿足設計指標0.25 mm要求。

4.2 遺傳算法公差優化

遺傳算法公差優化流程如圖10所示。

根據上述模型，選取不同公差等級組合方案，對該型液力變矩器各零件裝配環進行優化。遺傳算法參數如下：初始種群規模100，交叉概率0.8，變異概率0.05.

4.3 裝配驗證

研究清楚徑向圓跳動值超差的作用機理后，基于徑向圓跳動形位公差傳遞模型，采用遺傳算法優化得到的最優方案，對變矩器零件的公差等級進行改進。

完成各零件公差等級調整優化后，對一批變矩器進行重新整裝，并對這一批次(共29臺)樣機的徑向圓跳動值進行測量。測量結果表明：優化改進后的樣件末端徑向圓跳動值分布于(0.20 mm,0.27 mm)之間(見圖11)，實測數值滿足了設計要求。

用高斯擬合曲線對比優化前后實測值的分布范圍，如圖12所示。

由圖12可知，優化前徑向圓跳動平均值較大，分布范圍較寬，基于徑向圓跳動形位公差傳遞模型優化后的徑向圓跳動平均值更小，分布范圍更小，且能符合實際工程要求。

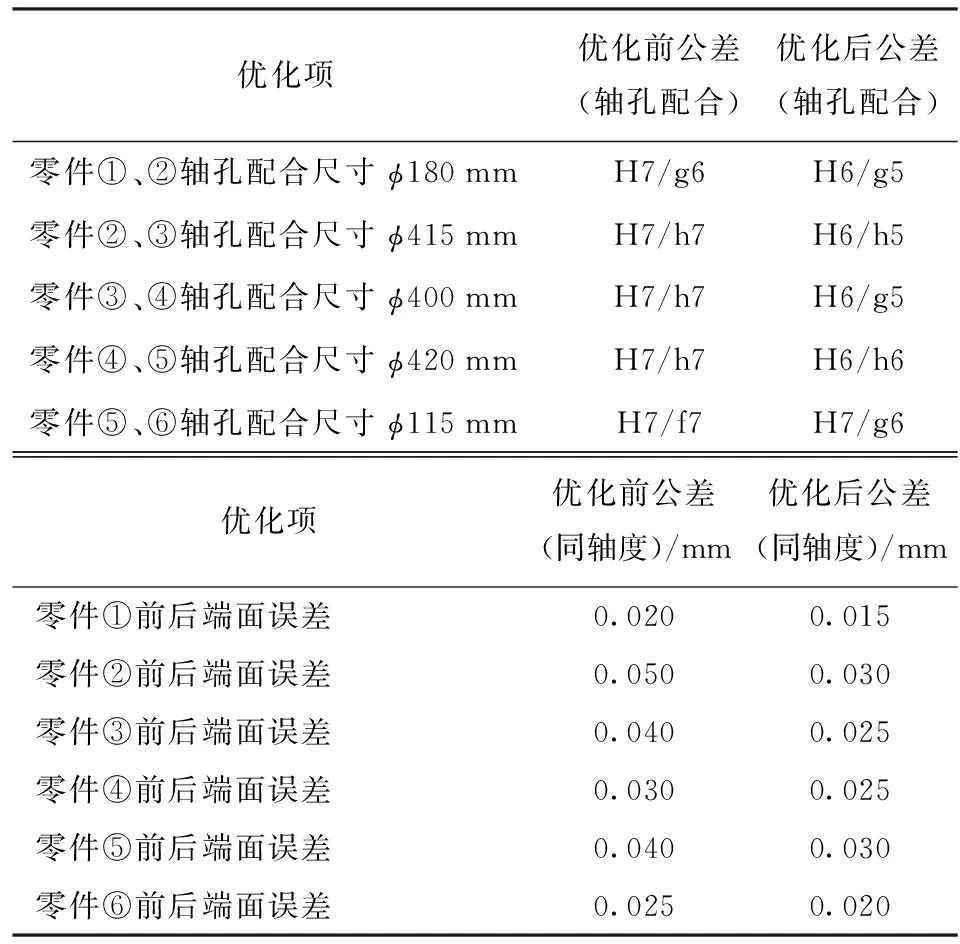
表3 最優方案的具體參數

5 結論

在旋轉機械軸系裝配體當中，配合面是多種誤差傳遞的媒介。多種類型誤差通過配合面耦合之后，傳遞的機制較為復雜。本文結合旋轉機械軸系裝配體幾何特征，以液力變矩器為實例，提出了徑向圓跳動位置公差的分析模型。考慮不同類型誤差對累積精度的作用不同，拓展蒙特卡洛模擬法，建立了徑向圓跳動位置公差累積精度計算模型。通過多組試驗數據分析，得出以下主要結論：

1) 多零件裝配的旋轉機械軸系裝配體徑向圓跳動位置誤差是可預測的，且符合一定的分布規律；本文所提變動邊界圓方法和徑向圓跳動形位公差裝配體傳遞模型為誤差分析奠定了基礎。結合蒙特卡洛法擬合出徑向圓跳動公差均值及其分布規律，與產品實際測量值相符合。

2) 采用遺傳算法對于旋轉機械軸系裝配體位置公差優化問題具有較高的適用性和計算精度。

3) 工程實例結果表明，本文所提的多目標優化模型用于指導圓跳動公差設計具有可行性和實用性。依據本文提出的徑向圓跳動形位公差裝配體傳遞模型，可對旋轉機械軸系裝配體設計進行優化。