不同建模方式對規則橋梁地震反應的影響研究

陳登峰

（浙江西城工程設計有限公司，浙江 杭州 310023）

0 引言

正確地建立橋梁結構的空間動力模型是進行橋梁抗震分析的基礎。本文研究的規則橋梁指的是各橋墩高度相等、截面相同、橋梁跨徑相等、梁體等截面的連續梁橋，屬于抗震設計規范中定義的普通標準橋梁。地震分析時，對其上部結構通常采用精細模型、梁格體系模型和單梁模型三種方式進行模擬。

從理論上說，采用精細模型計算結果相對準確，但建模較為復雜、計算工作量大。與之相比，后兩種模型的計算工作量大大減少，但其計算精度是否符合工程要求，需要進一步驗證。因此，本文采用反應譜分析法對三種模型對規則橋梁的結構動力特性和地震反應的影響進行研究。

1 計算模型的建立

本文的研究是以先簡支后連續的T梁橋為背景。橋梁跨徑為6×40 m，上部結構橫向由6片T梁組成，橋寬13.25 m，材料為C50混凝土，主梁截面見圖1。橋墩為雙柱式墩，柱徑為2 m，樁徑為2.2 m（見圖2），兩端橋臺設滑板式橡膠支座，支座型號為300 mm×450 mm×52 mm。其他橋墩頂設板式橡膠支座，支座型號為450 mm×550 mm×92 mm。

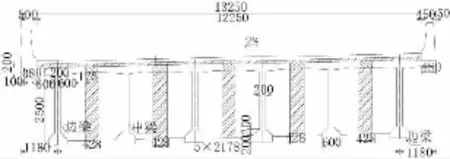
圖1 典型T梁橫斷面圖(單位：mm)

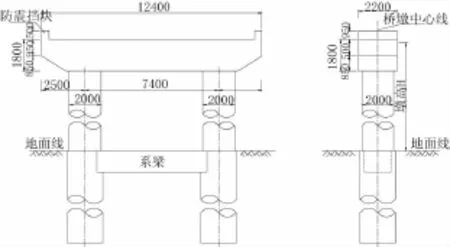
圖2 橋墩一般構造圖(單位：mm)

1.1 精細動力分析模型

精細模型中上部結構6片T梁的橋面板用板單元模擬，梁肋和橫隔板采用空間梁單元模擬，橋墩采用空間梁單元進行模擬。

（1）上部結構的模擬

精細模型中上部結構6片T梁的橋面板采用板單元模擬，T梁之間的橫隔板采用梁單元模擬。全橋模型見圖3。

（2）橋墩的模擬

橋墩采用空間梁單元進行模擬。橋墩蓋梁根據上部構造的橫向布置來劃分梁單元。橋墩根據墩高的不同劃分單元。

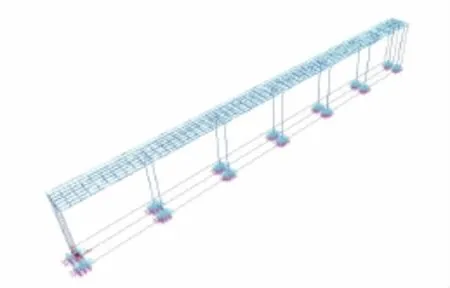
圖3 精細計算模型

（3）橡膠支座的模擬

板式橡膠支座采用線性彈簧連接單元模擬，橫向6片梁底均設1片板式橡膠支座，其剪切剛度k根據公式（其中：Gd為板式橡膠支座的剪切模量；Ar為橡膠支座的剪切面積；為橡膠層的總厚度）計算。因為橫橋向一般都設計擋塊，因此橡膠支座橫向固結。豎向不考慮橡膠的壓縮，按固結考慮。

（4）樁基礎的模擬

在橋梁的地震反應分析中，樁基礎的一種常用處理方法是在承臺底部加上六個方向的彈簧來模擬樁基礎的作用（見圖4），并由承臺底部的內力按照靜力方法反推單樁最不利受力。彈簧剛度根據土層狀況和樁的布置形式按靜力等效的原則確定，其中土性資料一般根據m法確定。

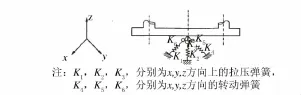
圖4 樁基礎六彈簧模型

2.2 梁格動力分析模型

梁格體系動力分析模型中6片T梁分別采用6個梁單元模擬，6片T梁之間橫隔板采用梁單元模擬。除上部結構的處理與精細模型不同外，其余均同精細模型。全橋計算模型見圖5。

圖5 梁格計算模型

2.3 單梁動力分析模型

單梁模型的動力分析模型除上部結構的建模與精細模型不同外，其余均同精細模型，單梁模型中上部結構6片T梁的等效成全截面單梁采用梁單元模擬，T梁之間的橫隔板作為節點荷載和質量加在節點上，橋面鋪裝作為均布荷載和質量加在梁單元上。其計算模型見圖6。

圖6 單梁計算模型

3 不同建模方式對結構動力特性的影響

為了更全面的考察三種不同建模方式對梁橋動力特性的影響，以三種建模方式對橋墩為10 m、20 m、30 m高度的梁橋進行了動力分析，得出各模型的動力特性如表1～表3所示。

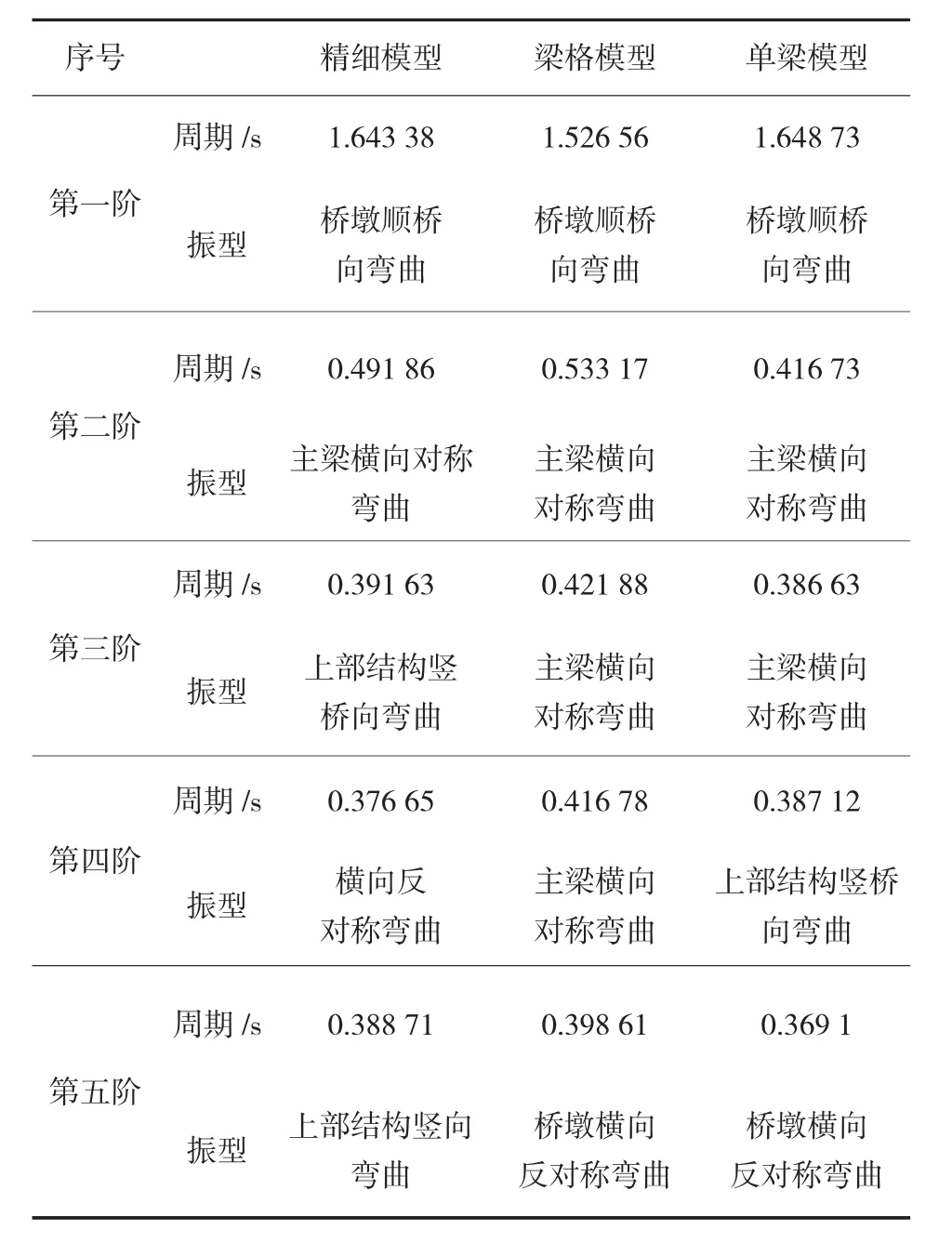
表1 不同模型的主要振型和主要特征周期表（墩高10 m）

對于梁橋而言，較為重要的振型為兩種，一是橋墩順橋向彎曲振型，二是主梁橫向對稱彎曲振型。對于前者，從表1～3中可以看出，三種模型的周期計算結果差別并不大，單梁模型和精細模型的計算結果吻合得較好，梁格模型計算結果稍差，但差別控制在5%以內。對于主梁橫向彎曲振型，單梁模型與精細模型吻合得較好，梁格模型橫向周期較其它兩種模型的周期長，是由于梁格模型在考慮各片主梁間橫向連接時僅考慮了主梁之間的橫隔板連接，未考慮主梁之間的橋面板的橫向連接作用，致使梁格模型的橫向剛度較精細模型和單梁模型小，因此，其橫向振型的周期長。

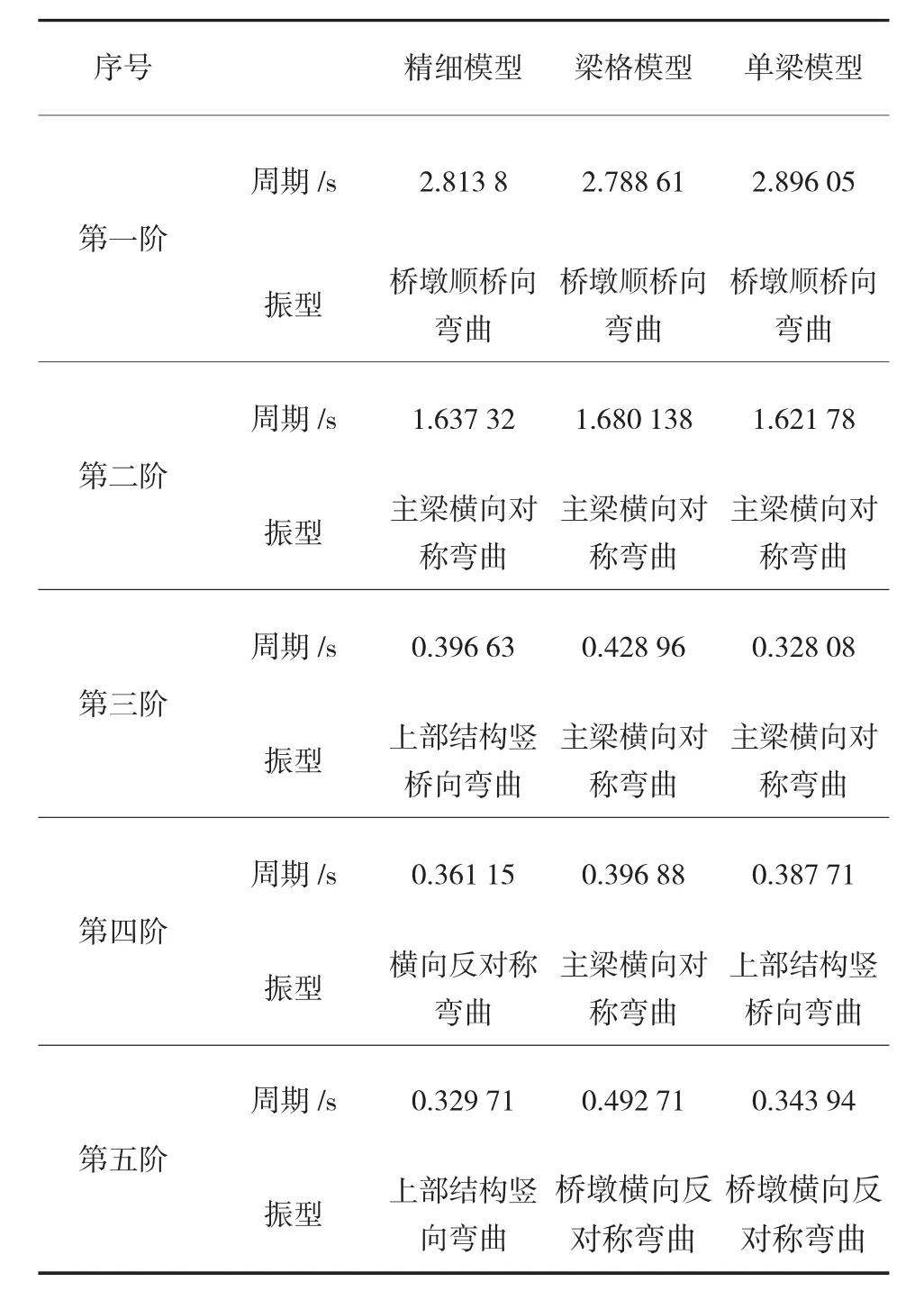
表2 不同模型的主要振型和主要特征周期表（墩高20 m）

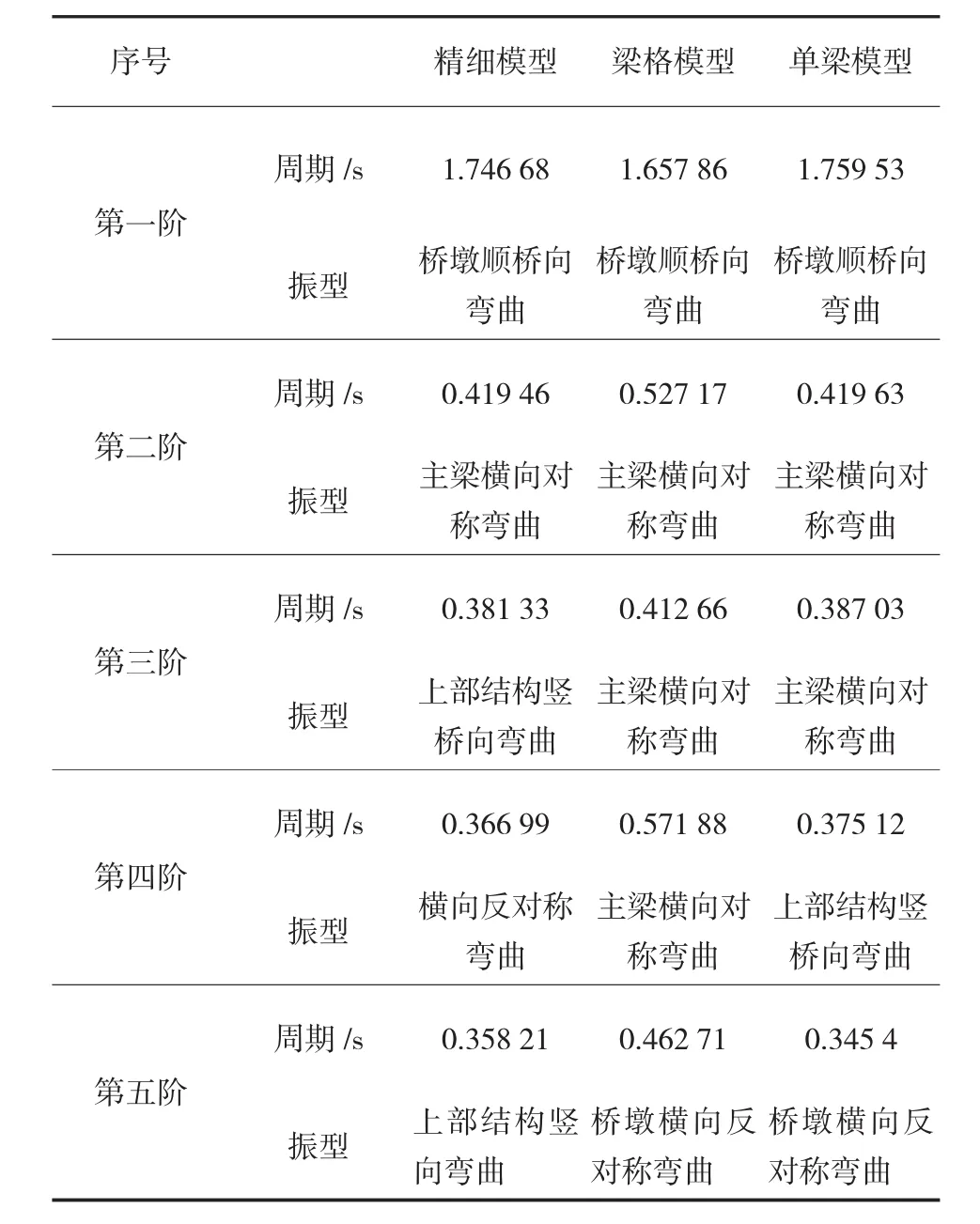
表3 不同模型的主要振型和主要特征周期表（墩高30 m）

4 不同建模方式對結構地震響應的影響

采用《公路橋梁抗震設計細則》（JTG TB02—01—2008）的反應譜作為地震動輸入，分別計算了縱向地震輸入和橫向地震輸入下三種模型的不同墩高10 m、20 m、30 m和不同的場地條件的地震響應，在結果分析中不計結構重要性系數。

我國《公路橋梁抗震設計細則》（JTG TB02-01-2008）將場地劃分為四類，其水平設計加速度反應譜見圖7，具體計算公式為：

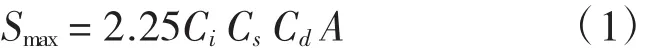
式中：Ci為抗震重要性系數；Cs為場地系數；Cd為阻尼調整系數；A為水平向設計基本地震動加速度峰值，g。

圖7 水平設計加速度反應譜

4.1 不同建模方式對不同墩高的橋梁地震響應影響

為了研究不同墩高下，建模方式對地震響應計算的影響，本節采用精細模型、梁格模型、單梁模型三種建模方式，以Ⅱ類場地條件為例，分別對10 m、20 m、30 m墩高的橋梁進行反應譜分析，假定精細模型計算結果為準確結果，將梁格模型、單梁模型計算結果與之相比較，得到梁格模型與單梁模型的計算誤差，結果如表4～表6所示。

從表中可以看出，對于不同墩高的梁橋，采用單梁模型建模的計算結果和精細模型相比，縱向和橫向地震響應計算結果的差別都是較小的，橫向響應的最大誤差為3.01%以內，縱向響應的最大誤差僅為1.81%。

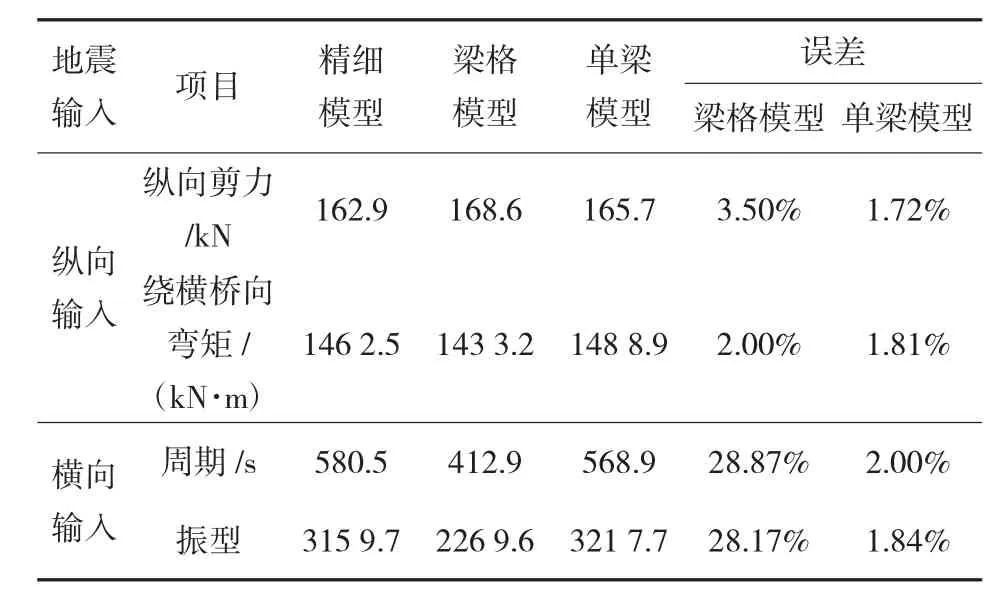
表4 不同模型的結構地震反應（墩高10 m）

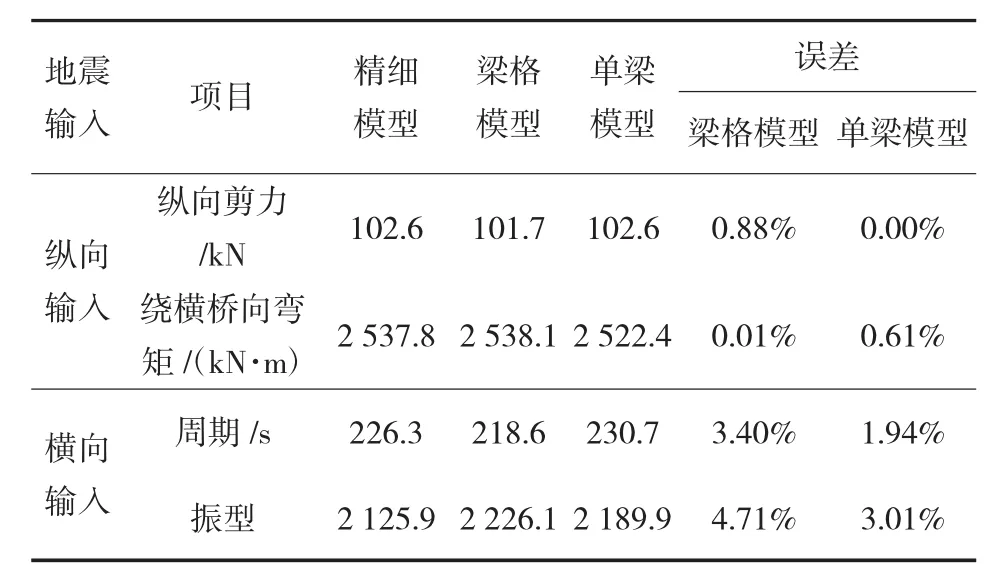
表5 不同模型的結構地震反應（墩高20 m）

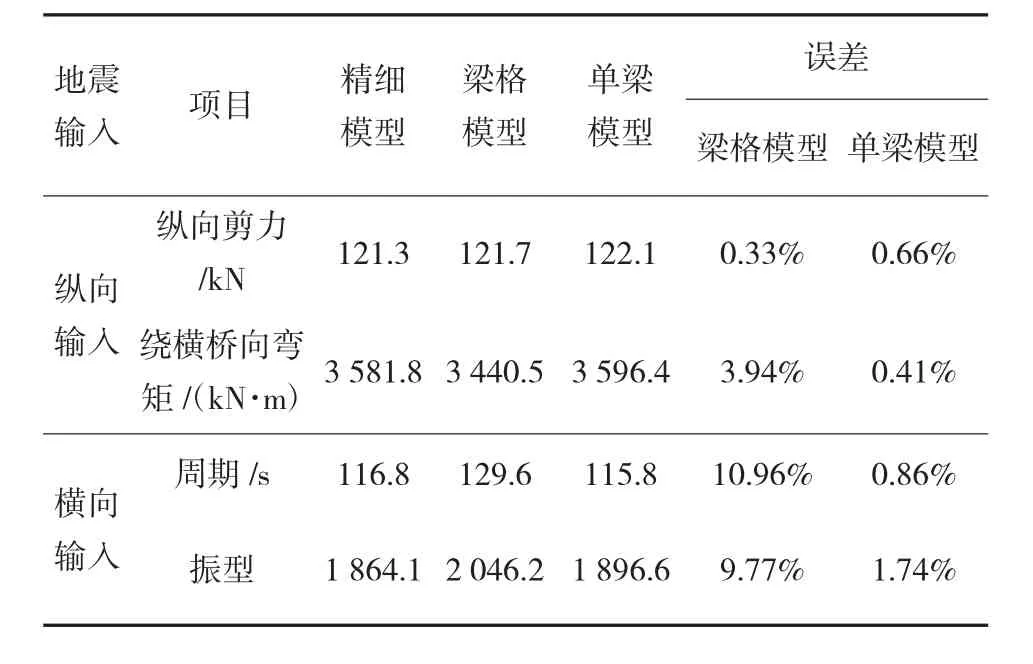
表6 不同模型的結構地震反應（墩高30 m）

5 結語

本文通過對T梁配雙柱式橋墩的多跨連續梁橋建立三種不同的模型進行對比分析，分別研究了三種建模方式對不同橋墩高度橋梁的結構動力特性的影響和地震響應的影響、不同場地條件地震動輸入的橋梁地震響應的影響，可得出以下結論：

（1）三種模型在橋墩順橋向彎曲振型和主梁橫向對稱彎曲振型中，周期計算結果差別并不大，單梁模型和精細模型的計算結果吻合得較好，梁格模型計算結果稍差，但差別控制在5%以內。

（2）對于不同墩高的梁橋，在II類場地地震輸入時，采用單梁模型建模的計算結果和精細模型相比，縱向和橫向地震響應計算結果的差別都是較小的，橫向響應的最大誤差為3.01%以內，縱向響應的最大誤差僅為1.81%。梁格模型的誤差稍大于單梁模型。

（3）對不同墩高的梁橋模型，在不同的場地地震輸入作用下，采用單梁模型計算的誤差是較小的，可以達到建模方便簡單而計算精度又能滿足工程需要的結果。