有間索的雙塔無(wú)背索斜拉橋索力參數(shù)敏感性*

陳一赫 孫亭亭 梁亞蘭 楊蔣鶴立 周興宇

(武漢理工大學(xué)交通學(xué)院1) 武漢 430063) (中國(guó)市政工程中南設(shè)計(jì)研究總院有限公司2) 武漢 430010)

0 引 言

斜拉橋設(shè)計(jì)是國(guó)內(nèi)橋梁常見的設(shè)計(jì)形式，對(duì)于橋梁的敏感性分析也比較成熟，對(duì)于矮塔斜拉橋、大跨度斜拉橋、獨(dú)塔斜拉橋、無(wú)背索斜拉橋[1-6]等各種設(shè)計(jì)形式，各橋梁工作者及高校已有相當(dāng)多的分析，但在主、副雙塔之間加以斜拉索連接的無(wú)背索斜拉橋的設(shè)計(jì)形式還較罕見.中間拉索的存在會(huì)極大地影響主、副橋塔的塔根應(yīng)力及塔身偏移，且在主、副塔構(gòu)造不對(duì)稱的情況下受力會(huì)更加復(fù)雜.橋塔在縱橋向及橫橋向均有一定角度的偏位，這對(duì)于橋塔的受力分析帶來(lái)一定的困難，其某些部位對(duì)于索力變化也更具敏感性.有間索的雙塔無(wú)背索斜拉橋的拉索在橋塔不同方位有多種布置形式，結(jié)構(gòu)的相關(guān)參數(shù)敏感性不明確.此類異形橋塔設(shè)計(jì)獨(dú)特新穎，所以對(duì)其進(jìn)行相關(guān)研究很有必要.本文通過(guò)對(duì)索力的整體變化分析及RSM響應(yīng)面法求解關(guān)鍵截面對(duì)不同套索的敏感因子，說(shuō)明有間索的雙塔無(wú)背索斜拉橋的索力敏感性.

1 工程背景

橋梁采用(108 m+70 m)V形塔雙索面斜塔斜拉橋，整幅布置，標(biāo)準(zhǔn)寬度為47 m，主梁采用鋼-混混合梁；塔柱采用矩形塔，主塔上塔柱高70 m，總高92 m，副塔上塔柱高50 m，總高72 m，其中下塔柱高約18.6m；塔柱順橋向?yàn)閂形，橫橋向?yàn)棣危骺缂斑吙鐐?cè)均設(shè)置8對(duì)斜拉索.橋塔及主梁連接處為固結(jié)設(shè)計(jì)，位于主、副橋塔中間段的主梁為塔梁固結(jié)段.

全橋共設(shè)置24對(duì)共48根斜拉索，分別為M1～M8，S1～S8，B1～B8.其中M1～M8 斜拉索一端錨固于主塔，一端錨固于副塔并于主塔頂進(jìn)行張拉；S1～S8一端錨固于副塔，一端錨固于鋼梁并于副塔頂進(jìn)行張拉；B1～B8 斜拉索一端錨固于副塔，一端錨固于混凝土梁并于副塔頂進(jìn)行張拉.M系列索即為中間拉索.

2 RSM響應(yīng)面法

2.1 RSM響應(yīng)面法基本原理

在實(shí)際工程活動(dòng)中，某個(gè)結(jié)果通常受到多個(gè)因素的共同影響，而各個(gè)因素對(duì)其影響程度不盡相同，一般通過(guò)對(duì)參數(shù)變化進(jìn)行實(shí)驗(yàn)分析可以定性分析某個(gè)變量對(duì)于結(jié)果的影響趨勢(shì)，但是不同變量對(duì)結(jié)果的影響程度僅靠單獨(dú)的參數(shù)變化實(shí)驗(yàn)難以定量估計(jì)，且結(jié)構(gòu)相應(yīng)函數(shù)通常為隱形方程，不便計(jì)算[7].RSM響應(yīng)面法(response surface methodology)可以直接利用廣泛的有限元分析程序，通過(guò)擬合多維曲面，近似表達(dá)結(jié)構(gòu)響應(yīng)函數(shù)，將實(shí)際的結(jié)構(gòu)隱性響應(yīng)方程轉(zhuǎn)化為方便計(jì)算的顯式方程，效率較高，精度符合工程需求.

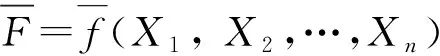
一種是Wong提出的含交叉項(xiàng)的二次多項(xiàng)式結(jié)構(gòu)響應(yīng)方程[8]：

(1)

式中：Xi,j(i,j=1,2,…,n)為影響因素；a,bi,cij(i,j=1,2,…,n)為待定系數(shù).

另一種是Bucher-Bourgund包含二次平方項(xiàng)但不包含二次交叉項(xiàng)的多項(xiàng)式響應(yīng)結(jié)構(gòu)方程[9-13]：

(2)

式中：Xi(i=1,2,…,n)為影響因素；a,bi,cj(i,j=1,2,…,n)為待定系數(shù).

其中式(2)由于不包含二次交叉項(xiàng)，待定系數(shù)比式(1)少，在影響因素較多的情況下求解較快，但精度比式(1)低.

2.2 取樣方法及敏感因子

模擬結(jié)構(gòu)響應(yīng)函數(shù)的精度主要取決于插值點(diǎn)及插值點(diǎn)附近所選取的樣本點(diǎn)是否包括實(shí)際結(jié)構(gòu)的狀態(tài)信息，取樣方法對(duì)RSM的影響至關(guān)重要.傳統(tǒng)響應(yīng)面方法取樣實(shí)驗(yàn)設(shè)計(jì)技術(shù)有兩種: CCD(central composite design)法和BBD(boi-behnken design)法.CCD法樣本點(diǎn)由N維超立方體的角點(diǎn)、坐標(biāo)軸的軸點(diǎn)和中心點(diǎn)構(gòu)成.而BBD法樣本點(diǎn)則由N維超立方體的邊中點(diǎn)和中心點(diǎn)構(gòu)成，圖1為三因素BBD取樣試驗(yàn)設(shè)計(jì)方法示意圖.

圖1 三因素BBD取樣試驗(yàn)設(shè)計(jì)

(3)

3 索力整體變化敏感性分析

橋梁主、副塔上塔柱的截面應(yīng)力及主梁塔梁固結(jié)段是全橋結(jié)構(gòu)受力分析的重點(diǎn)部位，其中索力變化對(duì)于高橋塔斜拉橋產(chǎn)生的應(yīng)力及位移影響相當(dāng)顯著.通過(guò)對(duì)初始索力進(jìn)行-10%，5%，0%，5%、10%五個(gè)程度的索力值調(diào)整，計(jì)算主塔塔身偏位、副塔塔身偏位、主塔上塔柱截面應(yīng)力、副塔上塔柱截面應(yīng)力、主塔主梁固結(jié)區(qū)、副塔主梁固結(jié)區(qū)6個(gè)關(guān)鍵部位的響應(yīng)，分析其對(duì)于索力變化的敏感程度及敏感區(qū)域.有限元建模見圖2，全橋共704個(gè)單元，不考慮樁基礎(chǔ)影響，下塔柱底端為固定支座，主梁兩端為活動(dòng)鉸支座，除斜拉索為受拉桁架單元，其余均為梁?jiǎn)卧鞯姆蔷€性效應(yīng)采用等效彈性模量考慮.

圖2 全橋有限元模型

3.1 主、副塔塔身偏位

對(duì)全橋進(jìn)行監(jiān)控計(jì)算的一個(gè)重要指標(biāo)為主、副塔塔頂偏位，塔頂偏位決定了施工過(guò)程中的塔身預(yù)偏程度，是線形控制的顯著控制指標(biāo).通過(guò)對(duì)初始索力值調(diào)整計(jì)算，部分結(jié)果見圖3.由圖3可知，橋塔塔身位移變化與索力值變化為負(fù)相關(guān)，索力越大，位移變化越小，且為線性相關(guān).就豎向Z軸，主塔塔頂位移由27.173～22.241 cm，副塔塔頂位移由13.268～11.465 cm，由于主塔比副塔高約20 m，位移響應(yīng)更加明顯.主塔塔頂位移變化量與原索力塔頂下沉量之比為0.2，副塔為0.146.主塔上塔塔身位移響應(yīng)束從30 m高處開始進(jìn)行分散，副塔則從約40 m高處開始分散.相對(duì)主塔來(lái)說(shuō)，副塔塔身對(duì)于索力整體變化的響應(yīng)穩(wěn)定度更高，而主塔對(duì)于索力變化的敏感性更顯著.

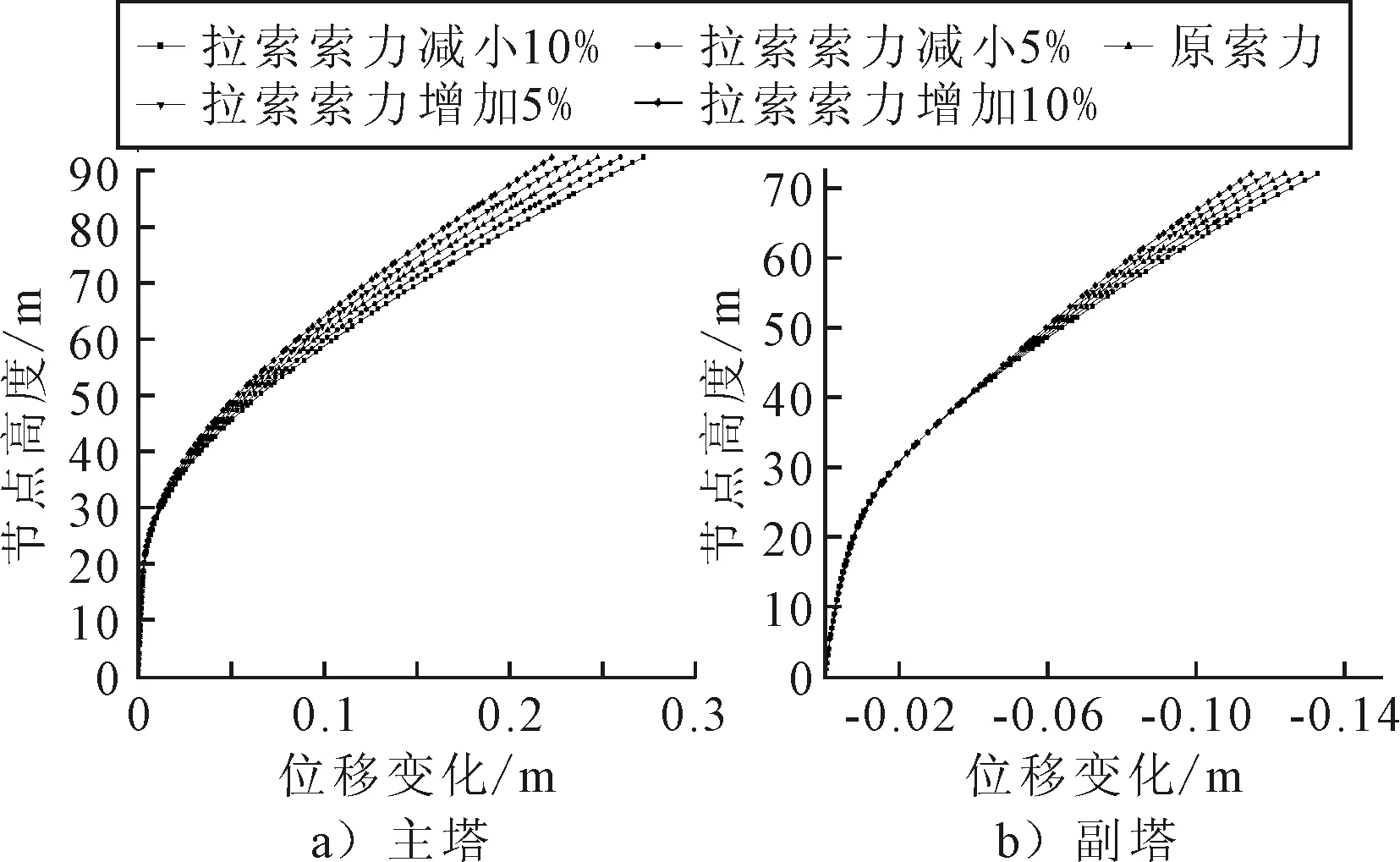
圖3 主、副塔塔頂Z方向位移

3.2 主、副塔上塔柱截面應(yīng)力

塔身截面應(yīng)力是劃分施工階段的主要參數(shù)指標(biāo)，對(duì)于上塔柱的單次容許施工高度具有決定性的作用，在后續(xù)監(jiān)控測(cè)量指標(biāo)中，塔身關(guān)鍵截面的應(yīng)力測(cè)量與數(shù)據(jù)分析是判斷橋梁工作狀態(tài)的絕對(duì)參數(shù)之一.分析結(jié)果見圖4.

圖4 主、副塔塔身截面應(yīng)力

由圖4可知，在最不利應(yīng)力組合的情況下，下塔柱主、副塔均不會(huì)出現(xiàn)拉應(yīng)力，在經(jīng)過(guò)塔梁固結(jié)段后，均會(huì)在上塔柱截面處出現(xiàn)最大拉應(yīng)力，拉應(yīng)力隨著截面高度的提升而不斷改變，塔頂5 m高橫梁處重新進(jìn)入全受壓狀態(tài).從索力變化情況看，主塔應(yīng)力響應(yīng)束在上塔柱塔根部位最為分散，后趨于集中；副塔應(yīng)力響應(yīng)束變化趨勢(shì)與主塔不同，其在塔根及塔頂附近應(yīng)力響應(yīng)束相對(duì)集中，而在43～53 m高處區(qū)域內(nèi)最為分散，說(shuō)明主、副塔對(duì)索力變化的塔身截面各區(qū)域的敏感程度不同.

3.3 主、副塔主梁固結(jié)區(qū)

橋梁塔柱材料為混凝土，與主梁連接為固結(jié)式，塔梁固結(jié)區(qū)為大體積混凝土的異形結(jié)構(gòu)，因此相互作用影響量比較可觀.索力變化引起塔柱截面應(yīng)力及位移變化進(jìn)而傳遞至主梁與橋塔連接的固結(jié)區(qū)，影響主梁的工作狀態(tài)，研究塔梁固結(jié)區(qū)的截面應(yīng)力變化是必要的.通過(guò)對(duì)主梁進(jìn)行計(jì)算分析得到部分結(jié)果見圖5.由圖5可知，在固結(jié)區(qū)主塔側(cè)，索力變化引起的主梁固結(jié)區(qū)應(yīng)力變化主要集中在內(nèi)側(cè)，即固結(jié)區(qū)內(nèi)，主塔固結(jié)區(qū)外側(cè)則受影響較小，應(yīng)力響應(yīng)束趨于集中；在固結(jié)區(qū)副塔側(cè)，主梁截面應(yīng)力響應(yīng)變化則集中在外側(cè)，即固結(jié)區(qū)外，應(yīng)力響應(yīng)束較分散，副塔固結(jié)區(qū)內(nèi)側(cè)受到的影響微弱.主梁沿縱向，橋梁先進(jìn)入副塔主梁固結(jié)區(qū)外側(cè)，然后進(jìn)入主梁固結(jié)區(qū)副塔內(nèi)側(cè)至固結(jié)區(qū)主塔內(nèi)側(cè)，最后從主塔固結(jié)區(qū)外側(cè)離開，在此路徑上，主梁截面應(yīng)力響應(yīng)束先變?yōu)榉稚⒍蠹校^而分散最后又趨于集中.表明索力變化對(duì)于主副塔兩側(cè)及主梁不同截面處的影響規(guī)律具有差異性.

圖5 整體分析主、副塔主梁固結(jié)區(qū)截面應(yīng)力

4 單套拉索RSM敏感性分析

全橋由S，M，B三套拉索體系構(gòu)成，且拉索的位置與長(zhǎng)度差異性較大，所以單套索對(duì)主塔塔頂位移、副塔塔頂、主塔上塔柱塔根截面應(yīng)力、副塔上塔柱塔根截面應(yīng)力、主梁固結(jié)跨中等關(guān)鍵節(jié)點(diǎn)的影響各不相同，對(duì)施工過(guò)程中的誤差控制重點(diǎn)也造成一定影響，進(jìn)行單套拉索的RSM敏感性分析是必要的.

計(jì)算采用的取樣方法為BBD實(shí)驗(yàn)取樣設(shè)計(jì)，通過(guò)對(duì)S，M，B三個(gè)影響因子的計(jì)算，歸納出關(guān)鍵部位分別對(duì)三套索的敏感因子，見圖6.

圖6 關(guān)鍵部位對(duì)S，M，B索的敏感因子

由圖6可知，對(duì)于主塔塔頂位移，M索的敏感因子絕對(duì)值最大，為1.001，表示索力每變化1%的值，主塔塔頂位移有1.001%的變化幅度；對(duì)于副塔塔頂位移，B索的敏感因子絕對(duì)值最大，為1.296，表示索力每變化1%的值，副塔塔頂位移變化1.296%；對(duì)于主梁固結(jié)段跨中部位，影響水平比較大的索為S，M索，敏感因子絕對(duì)值分別達(dá)到0.438、0.636，而B索敏感因子不足0.1，對(duì)主梁固結(jié)段跨中部位影響較小；對(duì)于主塔上塔根，M索的敏感因子絕對(duì)值最大，達(dá)到0.423，索力每變化1%，主塔上塔根部位的應(yīng)力變化有0.423%；對(duì)于副塔上塔根，三套拉索均有一定影響，S，M，B三套拉索的敏感因子絕對(duì)值分別為0.779，0.289，0.578，S索對(duì)于副塔上塔根部位的影響效果相對(duì)最為顯著.

5 結(jié) 論

1) 主、副塔塔頂位移與索力變化為負(fù)相關(guān)，且線性變化，隨著索力的增加，塔頂位移逐漸減小；通過(guò)RSM響應(yīng)面法求得主、副塔的敏感因子不同，影響主塔塔頂位移最大的為M索，影響副塔塔頂位移最大的為B索.

2) 主、副塔塔身截面應(yīng)力的變化趨勢(shì)具有差異性，主塔在索力整體變化時(shí)應(yīng)力響應(yīng)束在上塔柱塔根部位最為分散，而副塔則在上塔柱的中高段有明顯的應(yīng)力變化；影響主塔上塔根截面應(yīng)力最大的索為M索，副塔則受到三套拉索的共同影響，但相對(duì)顯著的為S索.

3) 主梁固結(jié)段隨索力變化的截面應(yīng)力相應(yīng)具有區(qū)域性，在主梁從副塔至主塔的路徑上，應(yīng)力變化從顯著到不顯著，又從顯著變化為不顯著，主、副塔各自區(qū)域內(nèi)的主梁固結(jié)段應(yīng)力響應(yīng)束的變化規(guī)律并不相同；同時(shí)影響主梁固結(jié)段跨中截面應(yīng)力最大的索為S和M索.

雙塔無(wú)背索斜拉橋的設(shè)計(jì)特點(diǎn)決定了自身的結(jié)構(gòu)受力性能較復(fù)雜，且通過(guò)本文分析來(lái)看，初始索力并不能滿足結(jié)構(gòu)的受力需求，在施工階段的計(jì)算中還需對(duì)索力進(jìn)行調(diào)整.