面向船型優化的船舶靜水力計算方法*

蔡寒冰 馮佰威 常海超

(武漢理工大學高性能船舶技術教育部重點實驗室1 ) 武漢 430063) (武漢理工大學交通學院2) 武漢 430063)

0 引 言

近年來，基于仿真的設計(simulation-腳based design，SBD)成為研究前沿的熱點課題.SBD技術將計算流體力學(computational fluid dynamics，CFD)技術、計算機輔助幾何設計(computational aided design，CAD)技術，以及優化算法等有機地結合到一起，形成了一種新的船型設計模式，具有高效、準確和適用性強等特點，被廣泛應用于船型優化設計.

優化問題包括設計變量、約束條件和目標函數.為了滿足工程實用性，約束條件在優化問題中起關鍵作用.具體到船型優化設計，一般會以靜水力數據作為約束條件，如為保證優化后的船型浮態不發生變化，選擇浮心位置作為約束；為不影響船舶的營運性，選擇排水量作為約束條件；為不影響船舶的技術性能，選擇濕表面積等作為約束.因此，在船型優化過程中，必須能夠實時計算船舶靜水力參數.

劉春雷等[1]使用加密型值表對47 500 t散貨船“太行128”進行計算，在型寬、型深及船長方向對船進行細分，讀取型值點后對型值點進行直接積分，得到了可靠的結果；王建勛等[2]使用三次樣條函數對型值表數據進行插值后反求樣條曲線上的點，對這些點積分得到橫剖面面積，最后用辛普森積分對橫剖面面積進行積分得到全船的排水體積；周念福等[3]對CATIA軟件進行了二次開發，使其可以直接對船體曲面切片，通過調用相關函數對這些切片進行計算，最后得出船體體積.

以上的幾種方法，加密型值表法及樣條函數法需要大量數據，對船型優化而言，計算比較繁瑣；基于商業軟件二次開發的靜水力程序需要對相關軟件進行集成，增加了集成的成本與難度，故該方法也不能很好地適應船型優化設計的需要.

基于此，為滿足船型優化的需要，本文采用了一種基于面元法的船舶靜水力計算方法[4]，該方法首先要提取船體曲面的型值點，再使用這些型值點建立二維參數面元，然后建立對單個面元的數學模型，最后對面元進行積分得到相應的靜水力性能數據.

1 船體型值點的提取

目前，三維船體模型多是基于非均勻有理B樣條(non-uniform rational B-spline ,NURBS)表達的，而NURBS曲面為

0≤u,v≤1

(1)

式中：wij為權因子；dij為控制頂點；Ni,k(u),Ni,l(v)分別為u向k次和v向l次的規范B樣條基，u、v則是節點矢量.

對于任意曲面，獲取了曲面NURBS的次數、控制點，以及權因子的信息，可以求得曲面上的點的型值.例如，要在曲面上取100個型值點(此處u方向取10個值，v方向取10個值，記為10×10)，就可以分別對u、v取0/9，1/9，2/9，…，9/9，帶入到式(1)中，得到相對應的型值點數據.NURBS原理和算法見參考文獻[5].

根據上述方法，就可以獲取船體曲面上的離散型值點.本文對DTMB5415船型的型值點進行了提取，見圖1.該船型有三個面，本文對每個面取30×20，即在方向取30個值，方向取20個值，得到了如圖1的型值點點云.同時，對得到的型值點進行點/曲面偏差分析，得到這1 800個型值點與曲面的平均距離為2.428×10-7m，滿足船型優化的精度要求.

圖1 船型DTMB5415型值點提取

2 基于面元法的靜水力計算原理

基于面元法的靜水力計算方法首先將船體曲面離散為二維參數面元， 再依據高斯定理，將對船體的三維體積分轉化為對面元的二維面積分，最后對所有面元進行積分，就可以得到該船的靜水力性能數據.

2.1 二維參數面元的建立

根據第一節所述的提取型值點的方法提取船體曲面的型值點，將這些型值點按順序劃分為四邊形單元，每一個單元可以看作是一個面元，船體面元見圖2.而從船體曲面上提取出的單個面元，見圖3，其中，是任意面元的四個角點.

圖3 船體單個面元

[6]

(2)

式中：xi,yi,zi(i=1,2,3,4)分別為單個面元的四個節點坐標值；(ξ,η)為圖4中所示的等參坐標；Ni為二維線性形函數，其表達式為

(3)

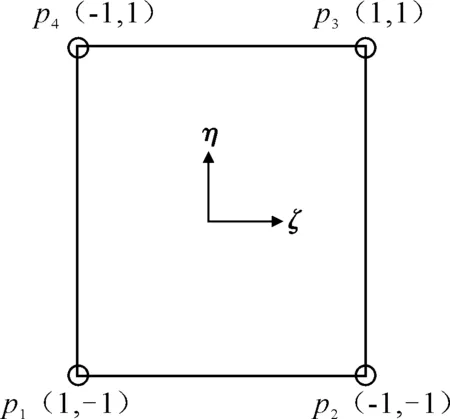
圖4 4節點面元等參坐標

2.2 基于高斯定理的靜水力計算模型

船舶水下體積V是由船體濕表面Swet和水線面Swl圍成，根據高斯定理(4)式，可以將對船體的三維體積分轉化為對面元的二維面積分.再根據具體問題，取適當的P,Q,R值，就可以求得相應的靜水力性能數據.

(4)

選取P=v,Q=y,R=0，根據式(5)就可以求得船舶的排水體積：

(5)

選取P=0.Q=y2/2,R=0，根據式(6)就可以求得船舶的浮心縱向位置.

(6)

同理，水線面面積、濕表面積、中橫剖面面積為

(7)

橫穩性半徑、縱穩性半徑可由式(8)計算得：

(8)

各船型系數為

CB=

Cp=

Cvp=

(9)

2.3 面元上函數數值計算

根據2.1內容，船體曲面上的面元被轉換成了二維參數線性面元，且每一個面元都是正則的，則每一個面元的法向量可為[7]

(10)

式中：J為雅克比行列式；Υξ(ξ,η),Υη(ξ,η)分別為面元切平面內ξ方向、η方向的方向矢量.

根據高斯-勒讓德積分公式，則船體積分為

(11)

式中：m1,m2為節點數，由于本文采用2×2的二維線性參數單元，即此處為2；wi,wj為高斯求積公式的加權系數，本文中為1；參數ξi=±0.577 350 269 2;ηi=±0.577 350 269 2.

3 船舶靜水力計算結果及對比

本文開發了基于面元法的船型靜水力計算程序.同時，為了驗證上文原理的有效性和程序的實用性，分別用商業軟件maxsurf和本程序對母型船的靜水力性能進行了計算，并選取了排水體積、浮心縱向位置、濕表面積以及方形系數四個參數進行了對比.

KCS船型和S60船型的每個面點數取80×30，對每個船型的設計水線處的靜水力性能進行計算，即KCS船型取0.341 8 m處水線(記為0.341 8水線，同時若沒有特別說明，水線的單位均為m)，S60船型取0.163水線.此時，所用KCS船型船模有四個面，采用第一節所述的方法對船型曲面進行離散，離散的型值點共有9 600個；S60船模有二個面，離散的型值點共有4 800個.計算結果分別見表1～2.

表1 KCS船型maxsurf計算結果與程序計算結果對比

表2 S60船型maxsurf計算結果與程序計算結果對比

本文選取DTMB5415船型，每個面取80×30，并選取3條水線，分別為0.15水線、0.248水線和0.35水線進行計算.所用DTMB船型船模共有3個面，離散的型值點共有7 200個.計算結果分別見表3～9.

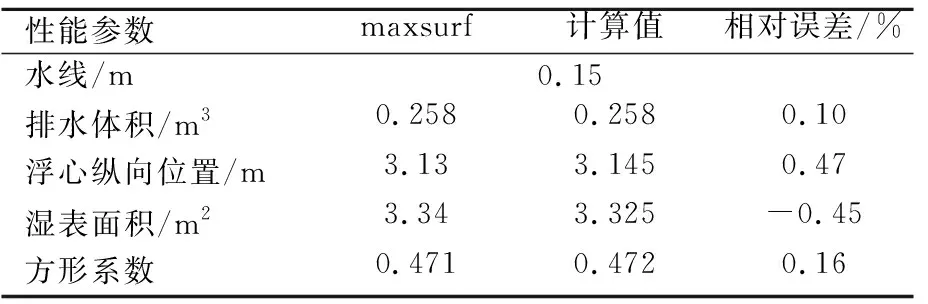
表3 80×30點數下0.15水線處DTMB5415船型maxsurf計算結果與程序計算結果對比

本文對DTMB5415船型分別再取30×20，50×30，100×30三種密度的型值點，計算該船型在設計水線處的靜水力性能.計算結果見表6～8.

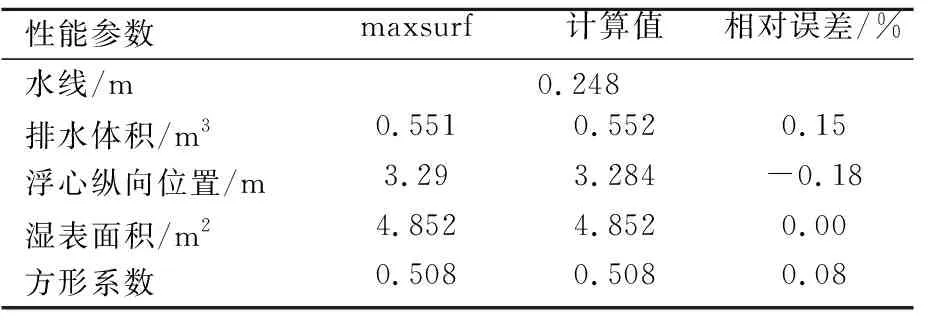
表4 80×30點數下0.248水線處DTMB5415船型maxsurf計算結果與程序計算結果對比

表5 80×30點數下0.35水線DTMB5415船型maxsurf計算結果與程序計算結果對比

表6 30×20點數下0.248水線處DTMB5415船型maxsurf計算結果與程序計算結果對比

表7 50×30點數下0.248水線處DTMB5415船型maxsurf計算結果與程序計算結果對比

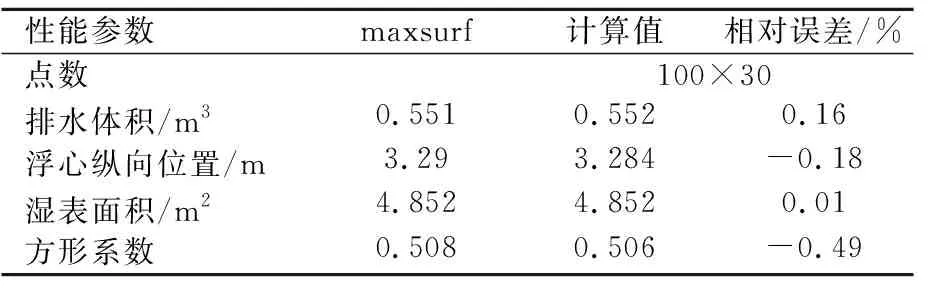
表8 100×30點數下0.248水線處DTMB5415船型maxsurf計算結果與程序計算結果對比

表9 不同船型在不同點數下的計算時間 s

表9中的計算時間是在不同的點數下，按該船型型深平均取5條水線，對這5條水線的計算時間取平均數所得.

由表1～2和表3～5可知，基于面元法的靜水力計算方法可以較好地計算不同的船型、不同的水線，具有良好的適用性，同時具有較好的精度.

由表3～5可知，當水線越高時，計算結果越好.由于DTMB5415船型具有球鼻艏，當水線越低時，船體曲面變化越劇烈，此時，0.15水線處的精度相較于0.248水線以及0.35水線處的數據的精度較低，即曲面變化越劇烈，基于面元法的靜水力計算方法的精度越低，反之越高.

表4和表6～8可知，型值點越多，計算結果也越好.同時，當每個面的點數大于1 500個，全船總型值點數大于4 500個時，計算結果的誤差均在0.5%以下，可以很好地滿足船型優化設計的需要.同時，根據表9顯示，型值點數越多，計算時間越長.故當船型的型值點數大于4 500個時，本方法可以很好地進行船型優化的靜水力計算.

4 結 論

1) 基于面元法的船舶靜水力計算方法能很好地適應DTMB5415，KCS，S60等標準船型，具有良好的適用性.

2) 基于面元法的船舶靜水力計算方法具有較好的計算精度，滿足船型優化設計的需要.

3) 在船型優化中，基于面元法的船舶靜水力計算方法只需要預先設定好計算所需要的點數和計算水線，便可以對目標船型進行計算，集成到船型優化平臺上較為便捷；同時，由于其可以自動對船型優化過程中新生成的船型的三維曲面進行讀點計算，故其能較好地適應船型優化的需要；此外，該方法計算時間較短，對于需要計算大量船型的船型優化問題具有一定優勢.