大跨度鋼桁梁斜拉橋車輛荷載動力效應研究

何博文 周 偉 賴敏芝

(1.中交第二公路勘察設計研究院有限公司 武漢 430056； 2.湖北交投智能檢測股份有限公司 武漢 430050)

近些年來，由于鋼桁梁的可散拼特性及鋼絞線斜拉索運輸、施工的便捷性，鋼桁梁斜拉橋在山區大跨度橋梁有較多的應用，如新疆果子溝大橋[1]、湖北忠建河大橋[2]、貴州北盤江大橋[3]。大跨度鋼桁梁斜拉橋屬于高次高靜定結構，它在車輛動態激勵下的響應十分復雜，車速的不同也給耦合振動增加不確定性，因此，研究大跨度鋼桁梁斜拉橋在車輛行駛過程中的振動響應極具現實意義。

國內外有不少學者對斜拉橋的車橋耦合效應進行了分析研究[4-7]，并取得了豐碩成果，但對鋼桁梁斜拉橋的動力響應研究較少。本文在已有研究的基礎上，根據車-橋耦合基本原理，以鴨池河特大橋為工程背景，取55 t重車作為移動車輛并將其模擬為彈簧-質量塊模型，研究大跨度鋼桁梁斜拉橋在不同車速下結構的動力響應規律，以期為橋梁的結構健康監測及運營管理中特殊條件下制定限速標準提供依據。

1 背景工程

鴨池河大橋位于貴陽至黔西高速公路，為雙塔雙索面混合梁斜拉橋，跨徑布置為72 m+72 m+76 m+800 m+76 m+72 m+72 m=1 240 m，邊中跨比為0.275，橋型立面圖見圖1。大橋邊跨采用預應力混凝土箱梁，梁高8 m；中跨采用鋼桁梁結構，橫向設置2片主桁架，桁高7 m、寬27 m，節間長度8 m，標準節段長度16 m，橋面由正交異性鋼橋面板與7.5 cm澆筑式瀝青混凝土組成。主塔采用H形塔，均為矩形空心截面，貴陽側主塔高243.2 m，黔西側主塔高258.2 m，斜拉索采用鍍鋅鋼絞線斜拉索，單塔有24對斜拉索，全橋共192根。鴨池河大橋設計荷載為公路-Ⅰ級，設計車速為80 km/h。

圖1 鴨池河大橋立面圖

2 動力分析模型

2.1 車輛荷載與斜拉橋結構耦合振動模型平衡方程的建立

根據規范[8]，采用公路-Ⅰ級重車(總重550 kN)作為動力分析中的車輛荷載。根據車輛振動分析基本原理，車輛可根據其結構特性簡化為不同自由度的彈簧-質量塊模型[9-10],簡化后的車輛動力模型見圖2。

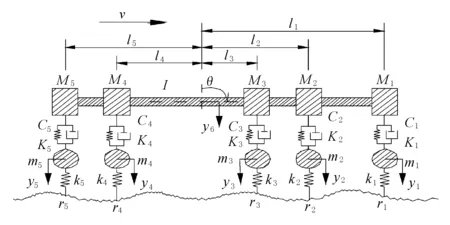
圖2 車輛動力模型

圖2中v為小車前行速度；mi(i=1,2,3,4,5，下同)為第i個軸的簧下質量，即車輪質量；Mi為第i個軸的簧上質量，即車身質量；ki為車輪剛度，Ki，Ci分別為懸架的剛度和阻尼；yi為車輪豎向位移，δi為主梁動撓度；y6為車身重心位置的豎向位移；θ，I分別為車身的轉角和懸架慣性矩；l1，l2，l3，l4，l5分別為各車身質量塊距離車身重心的距離；ri為第i個軸所在位置路面不平度。由于研究對象為理想狀態下車輛對結構的動力效應，故此處忽略路面不平度效應，即ri=0。

根據車身豎向位移平衡條件、車身轉動平衡條件、各車輪平衡條件可得

Ki(y6-liθ-yi)]=0

(1)

Ki(y6-liθ-yi)]=0

(2)

ki(yi+δi)=0,(i=1,2,3,4,5)

(3)

根據式(1)～式(3)，可將車輛的運動方程表示為式(4)矩陣形式

(4)

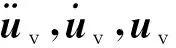
斜拉橋在車輛荷載作用下將會產生變形，且該變形是時變的，將反過來作用于車輛結構，進而影響車輛的運行狀態，如此耦合直至車輛通過橋跨結構。橋梁結構受車輛激勵的動力平衡方程可表示為式(5)矩陣形式[11]

(5)

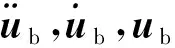
2.2 動力分析工況

模型中車輛由貴陽側行駛至黔西側。鴨池河大橋的設計車速為80 km/h，考慮到對于不良天氣條件下高速公路的限速原則[13]與個別車輛超速行駛的情況，選取20 ～100 km/h共5個動力分析工況進行研究，分析工況見表1。

表1 分析工況一覽表

3 分析結果

3.1 鋼桁梁豎向位移

由于邊跨混凝土結構整體剛度大，同時跨中位置的豎向位移最大，故取中跨跨中進行研究。提取ANSYS鋼桁梁節點位移結果，經整理可得中跨跨中豎向位移、加速度曲線見圖3，其中縱坐標為中跨跨中節點位移值、加速度值，橫坐標為車輛重心所處位置。

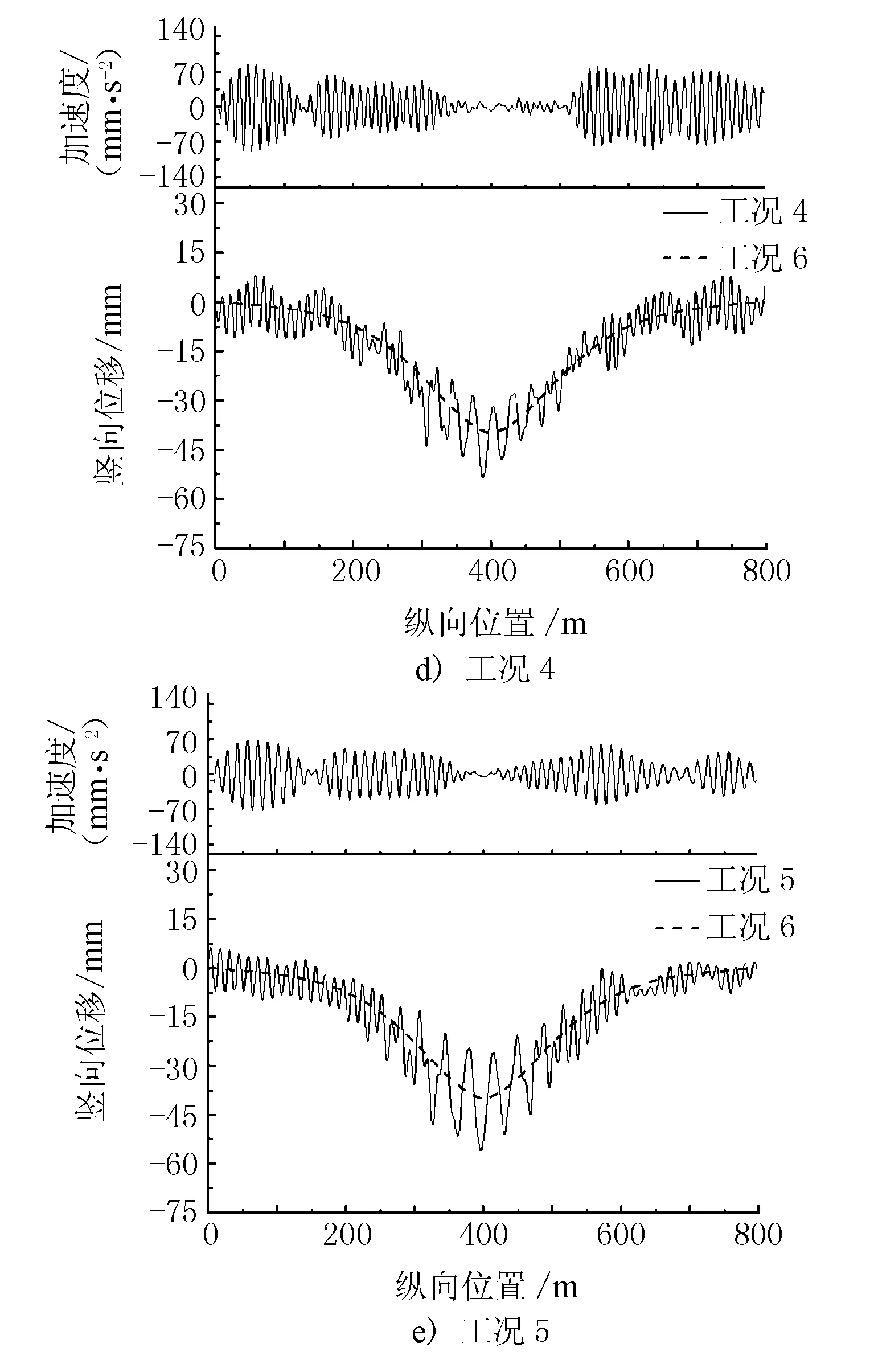
圖3 中跨跨中豎向位移、加速度曲線

由圖3可見，無論是何種車速，其跨中豎向位移時程曲線均是在靜力曲線基礎上浮動，且車輛速度越大，跨中的豎向位移振動幅值也就越顯著，其中工況1～工況5的跨中豎向位移曲線的最大相鄰波峰波谷差值分別為6.1，10.2，15.9，24.3，32.6 mm，而這些最大值均是在車輛行駛至跨中附近時產生的，但此時由于車輛自身質量的影響，使得跨中豎向加速度值較小。同時，車輛行駛在中跨近塔端時，跨中的豎向加速度明顯，且隨著車速的增加，跨中豎向加速度有增大趨勢，工況1～工況5的加速度幅值分別為58.6，70.2，161.5，173.2，141.6 mm/s2。中跨跨中豎向位移極值見表2。

表2 中跨跨中豎向位移極值 mm

由表2可見，低車速時跨中豎向位移最小值與靜力解很接近，其最大值亦較小；隨著車速的增大，跨中豎向位移的極值均有增大趨勢，車輛對結構的沖擊效應也越大。

3.2 鋼桁梁應力

鋼桁梁結構中弦桿是主要受力構件，且車輛作用下跨中位置的弦桿應力較大，故此處選取中跨跨中上、下弦桿進行研究，其中上弦桿軸向應力增量見圖4，下弦桿軸向應力增量見圖5，圖中弦桿軸向應力增量即車輛荷載作用下弦桿軸向應力實際值減去成橋時弦桿的軸向應力，由于低速情況下結構響應較小，限于篇幅，此處僅給出了工況3～工況5的動力響應情況。

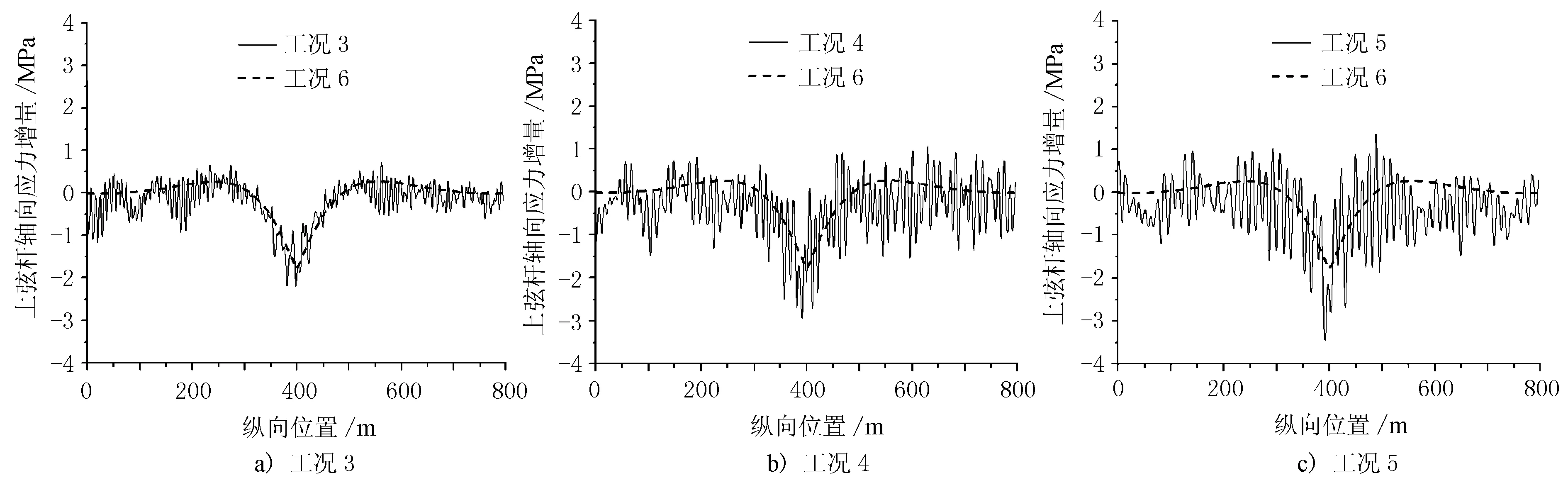
圖4 中跨跨中上弦桿軸向應力增量

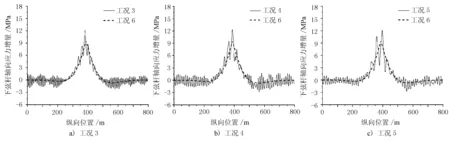
圖5 中跨跨中下弦桿軸向應力增量

由圖4、圖5可見，與跨中豎向位移的結論類似，跨中弦桿軸向應力增量的時程曲線也在靜力曲線基礎上浮動，且車速的增加會引起弦桿軸向應力響應程度的增大，其中工況5上、下弦桿軸向應力曲線的相鄰波峰波谷差值分別達到了3.8，8.6 MPa，高車速將對跨中下弦桿受力狀態產生很大的激勵作用。跨中弦桿軸向應力增量見表3。

表3 跨中弦桿軸向應力增量極值 MPa

由表3可見，低車速情況下跨中弦桿軸向應力的極值與靜力分析差別不大，但在工況3～工況5中，跨中弦桿的軸向應力浮動區間顯著增大，車速達到100 km/h時，跨中上、下弦桿的應力幅分別為4.8，15.4 MPa，說明車速越大，弦桿應力響應也越明顯。跨中上弦桿在各工況下的軸向應力幅值與靜力分析之比分別為1.092，1.413，1.417，1.947，2.335，跨中下弦桿在各工況下的軸向應力幅值與靜力分析之比分別為1.05，1.272，1.408，1.494，1.516，說明車速可直接影響弦桿應力的幅值大小。

4 結論

1) 車輛低速行駛時，鋼桁梁斜拉橋跨中豎向位移與弦桿應力的極值與靜力荷載相差較小，此時車輛對結構的沖擊作用較小；隨著車速的增大，跨中豎向位移與跨中弦桿應力時程曲線的振幅均顯著增大，結構的振動響應更加明顯。

2) 跨中豎向位移與弦桿應力的時程曲線均是在靜力荷載曲線基礎上浮動；當車輛行駛至跨中位置時，跨中的豎向位移與弦桿應力的振幅最大，但由于車身質量的作用，此時跨中位移加速度反而最小。

3) 當55 t重車的車速在100 km/h以內時，跨中的主梁豎向位移與構件應力幅值未產生激增現象，車速共振點不在該范圍內。