基于混合粒子群優化算法的橋梁有限元模型修正

鄒旭東 雷建平

(武漢理工大學交通學院 武漢 430063)

橋梁的初始有限元模型依據設計參數建立，通常與其實際工作狀況存在較大的誤差。為此，通過模型修正得到一個能夠真實反映橋梁結構靜、動力特性的有限元模型，為結構的安全評估及健康監測提供科學依據[1]。傳統的模型修正方法需要大量的原始數據進行迭代計算，且容易出現矩陣病態問題，求解效率較低。近年來，基于仿生學的優化算法發展迅速，為橋梁結構的有限元模型修正提供了一種新思路。

粒子群算法的基本思想起源于J.Kennedy和R.Eberhart對鳥群覓食行為的研究。該算法具有結構簡單、容易實現、魯棒性強等優點，在模型修正領域得到了廣泛的應用[2-4]。雖然粒子群算法的隨機搜索能力很強，但同時也存在易早熟收斂等缺點。為此，眾多學者在算法改進方面做了大量研究，提出了許多改進粒子群算法[5-7]，以增強算法的全局性搜索能力。

本文提出了基于混合粒子群優化算法的橋梁有限元模型修正策略。首先對標準粒子群算法采取自適應動態慣性權重策略改進，并引入差分進化算法以并行的方式進行混合優化；然后在模型修正中引入混合粒子群算法以修正模型的參數；最后通過某簡支梁數值模型的修正來驗證該算法的有效性。

1 標準粒子群算法和差分進化算法

1.1 標準粒子群算法基本原理及改進

1.1.1標準粒子群算法基本原理

在標準粒子群算法中，每個粒子的位置分別代表該優化問題的某個潛在最優解。粒子的性質由粒子的位置、飛行速度和適應度值3項指標確定[8]。其中，粒子適應度值是評判該粒子優劣程度的標準。每個粒子在可行解空間范圍內進行搜索時，通過個體極值和群體極值進行比較來更新自身的位置。粒子每次位置更新都需要重新計算粒子適應度值，并更新個體極值和群體極值的位置。

假設粒子群的粒子總數為M；優化問題可行解空間U的維度為N。則初始化的粒子種群可表示為：X=(X1,X2,…,XM)。其中Xi=(xi1，xi2，…，xiN)T表示第i個粒子(i=1,2,…,M)在解空間U內的位置。每個粒子Xi的適應度值則由該優化問題的目標函數來計算。粒子的速度可表示為Vi=(vi1，vi2，…，viN)T；個體極值可表示為Pi=(pi1，pi2，…，piN)T；群體極值可表示為Pg=(pg1，pg2，…，pgN)T。

在每次的迭代計算過程中，粒子的速度和位置更新算式如下。

(1)

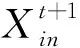
(2)

式中：w為慣性權重；n=1,2,…,N；i=1,2,…,M；t為當前迭代次數；Vin為粒子的速度；c1和c2為加速度因子；r1和r2為區間[0,1]內的隨機數。

1.1.2標準粒子群算法改進

在粒子群算法中，若慣性權重取值較大時，算法的全局探索能力顯著提升，搜索效率提高。反之，慣性權重越小，粒子的局部開發能力越強，算法的收斂速度加快。為提高算法的性能，本文采用自適應動態慣性權重策略對標準粒子群算法進行改進。將每一代的粒子按適應度值從優到劣排列，則排在第i位粒子的慣性權重的表達式為

wi=wmin+(wmax-wmin)(M-i)/(M-1)

(3)

加速度因子的表達式為

(4)

式中：wmin和wmax為預設的最小和最大慣性權重，本文中wmin取0.4，wmax取0.9。

1.2 差分進化算法基本原理

差分進化算法的基本思想是通過差分變異、交叉形成新的子代個體；然后基于“貪婪選擇”機制一對一篩選父代與子代中的優質個體組成新的種群。

1.2.1變異操作

差分進化算法的變異操作是通過任意2個或多個向量的差分信息來改變隨機選定的目標向量中的某些數值，變異公式為

(5)

式中：r1,r2,r3為種群中任意3個不同個體的編號；F為縮放因子。

1.2.2交叉操作

(6)

式中：Cr為交叉概率；j=1,2,…,N；jrand為[1,N]區間內的隨機整數。

1.2.3選擇操作

(7)

2 混合粒子群算法

2.1 混合粒子群算法思路

僅采用改進粒子群算法或差分進化算法在一定程度上仍存在易早熟收斂的問題，為此，本文將粒子群算法和差分進化算法以并行方式形成混合粒子群算法。混合算法將充分利用2種算法各自的優勢，將種群分為2個相同大小的子群，命名為P群和D群，分別采用粒子群算法和差分進化算法更新種群。為提高算法的搜索效率，避免算法陷入局部最優而導致搜索停滯，在2個子群之間建立一種信息交流機制。即在每次種群粒子更新后，選取P群和D群最優粒子中適應度值較好的粒子來指導2個子群下一代粒子的進化。當粒子群算法陷入局部最優點時，D群中的最優粒子信息將引導P群中陷入局部最優的粒子偏離原來的搜索方向，逃離局部極值點以較大概率向全局最優極值附近靠近。

2.2 混合粒子群算法流程

混合粒子群算法首先隨機初始化2個大小相同的子群P和D。其中P群采用自適應動態慣性權重的粒子群算法更新下一代粒子的位置和速度；D群則采用差分進化算法更新下一代粒子的位置。同時，在2個子群間引入信息共享策略來共享每代最優粒子信息，提高算法的搜索效率，避免粒子陷入局部最優。

設Pi和Pg分別為P群第t代粒子個體極值和群體極值；Dg為D群第t代粒子的群體極值；G為整個種群的群體極值。混合粒子群算法的具體操作如下。

1) 設置混合優化算法的參數，并隨機初始化2個大小相同的種群P和D。

2) 令t=0，計算2個種群所有粒子的適應度值。初始化P群粒子個體極值Pi、群體極值Pg、D群粒子的群體極值Dg和整個種群的群體極值G。

3) 根據方程(1)和(2)更新P群所有粒子的速度和位置，并更新Pi，Pg及其適應度值。其中，粒子速度更新采用的是整個種群的群體極值G。

4) 根據方程(6)～(8)對D群所有粒子進行變異、交叉、選擇操作，并記錄Dg及其適應度值。

5) 比較Pg和Dg適應度值的優劣，更新G及其適應度值。

6) 令t=t+1，檢查算法是否滿足終止條件。若滿足終止條件，則結束迭代，輸出粒子最優位置及其適應度值；若不滿足，則轉步驟(3)和(4)。

3 某簡支梁有限元模型修正數值模擬

3.1 簡支梁有限元分析

為驗證本文基于混合粒子群算法的橋梁有限元模型修正方法的可行性，對某計算跨徑為3 m的鋼筋混凝土簡支梁數值模型進行修正。簡支梁的設計截面尺寸如圖1所示，其中混凝土標號為C40，彈性模量3.25×104MPa，質量密度2 500 kg/m3。鋼筋的彈性模量2.0×105MPa，質量密度7 850 kg/m3。

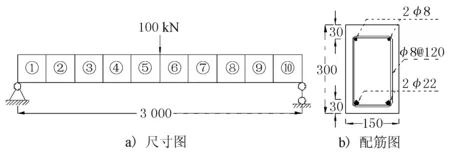
圖1 簡支梁模型示意圖(單位：mm)

采用ANSYS建立簡支梁的有限元模型，其中混凝土材料采用solid65實體單元模擬，鋼筋材料采用link180桿單元模擬。初始有限元模型見圖2。

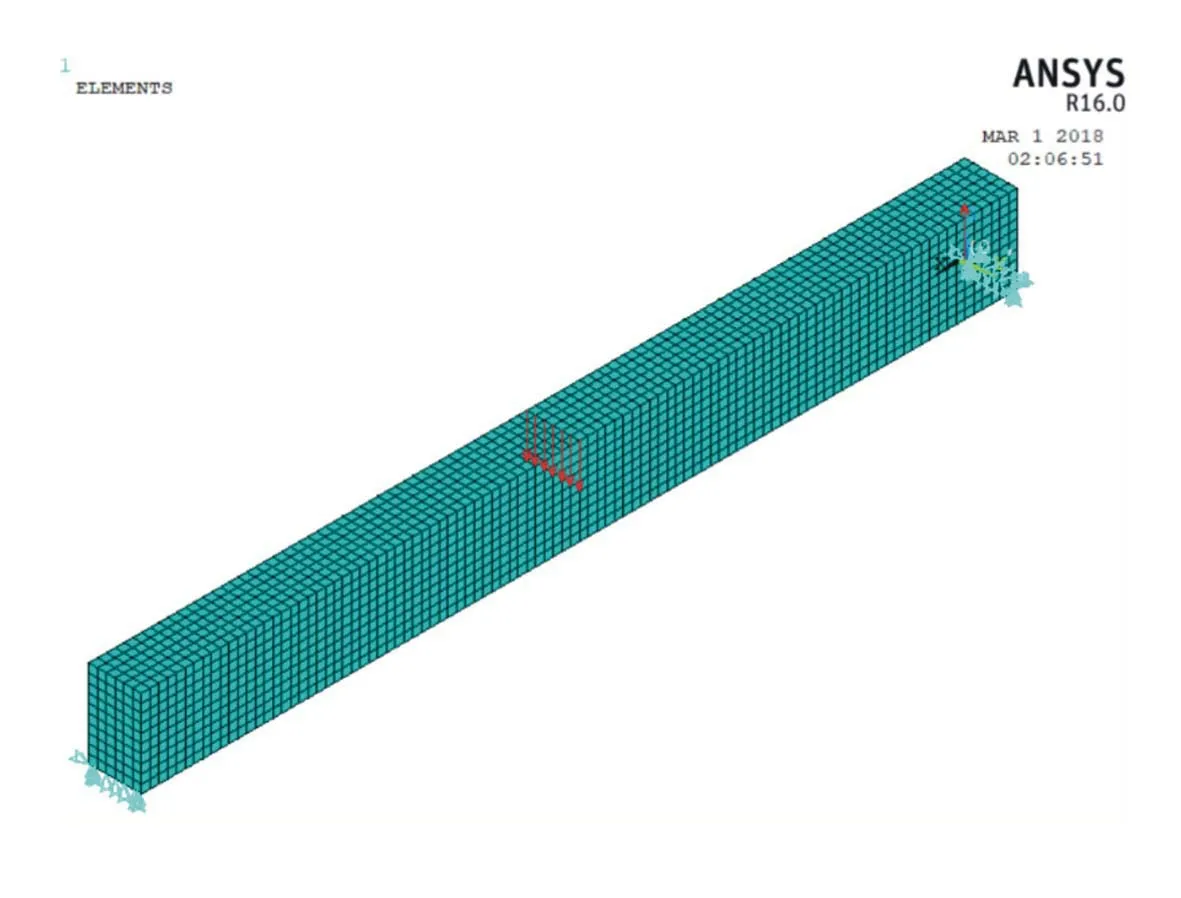
圖2 簡支梁初始有限元模型

對上述初始有限元模型第2，4，7段梁的混凝土彈性模量折減20%，作為本次數值模擬的真值模型。

3.2 簡支梁有限元模型修正

根據真值模型的撓度和頻率計算結果來構造聯合靜、動力的目標函數，修正目標函數如式(9)所示。

(9)

根據經驗法及靈敏度分析，選取混凝土彈模、鋼筋彈模和混凝土密度作為本次模型修正的修正參數。其中混凝土彈模和密度作為局部變量處理，鋼筋的彈性模量作為全局變量處理，共21個修正參數，參數的限值取參數設計值的±20%。

在MATLAB中采用混合優化算法對簡支梁有限元模型的參數進行優化。在混合優化算法中，隨機初始化2個規模均為50的種群，種群中每個粒子對應1個21維向量，每1維向量對應1個修正參數，迭代次數設為Tmax=500。

3.3 修正結果分析

經過500次迭代，最終得到兩種群中的最優粒子適應度值為8.72×10-5，修正后的有限元模型計算結果見表1。

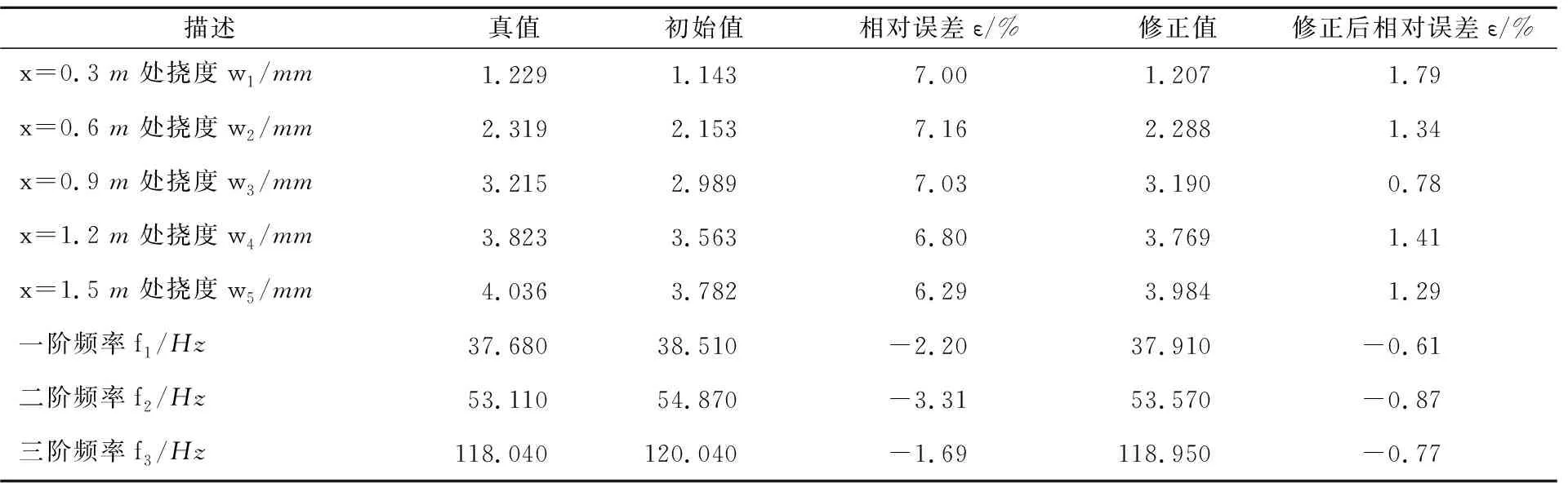
表1 有限元模型修正前后結構計算響應對比

由表1可見，撓度計算結果的相對誤差由修正前的7%左右降至2%以內，而頻率計算結果的相對誤差則由修正前的2%左右降低至1%以內，模型修正后的精度提升明顯，說明了混合粒子群算法對結構有限元模型的修正是可行的。

4 結語

本文在模型修正中引入混合粒子群優化算法修正模型參數，并采取自適應動態慣性權重策略改進，引入差分進化算法進行混合優化，改善算法的全局搜索能力。采用該方法修正后的簡支梁數值模型計算精度提升明顯，能夠真實反映結構的靜、動力特性，表明了該算法的有效性和可行性，為解決模型修正問題提供了一種新的思路。