混凝土梁橋應變監測分級預警閾值設定研究*

胡鐵明 汪子龍 韓基剛

(1.沈陽大學建筑工程學院 沈陽 110044； 2.遼寧省交通規劃設計院有限責任公司 沈陽 110005)

近年來已建橋梁在運營過程中發生特大安全事故的案例屢見不鮮，已建橋梁安全狀態的監控已經成為不可或缺的一項工作。混凝土應變是混凝土梁橋病害分析和狀態評估的關鍵參數，通過對混凝土應變的長期監測，可以了解結構的內力和應力分布情況，通過設定應變預警系統，對橋梁結構進行安全預警[1]。

目前對橋梁監測預警閾值的研究并不多，馬中軍等[2]引入t分布對彈性模量進行估計，采用修正后有限元模型模擬得到應變的區間預警閾值；李祥輝[3]通過有限元模擬結構受車輛荷載和溫度荷載作用，以包絡值為閾值設定依據；欒坤鵬[4]采用有限元軟件模擬結構受多種荷載組合作用，根據模擬結果確定閾值。可以看出，以上方法都是通過有限元模擬計算來確定預警閾值，但有限元模擬需要基于很多假定條件，計算結果與運營期橋梁真實狀態必然存在差異。

筆者通過線性回歸分離出應變監測中可變荷載作用效應值，基于日常監測與荷載試驗監測數據設定可變荷載作用效應值分級預警閾值，以期對某在役橋梁進行安全性預警。

1 工程概況

以遼寧省某混凝土梁橋(上行方向)為工程依托，該橋全長為990 m，共44孔，跨徑布置為10×20 m+8 m+26×20 m+52 m+80 m+52 m+18 m+3×20 m。設計荷載等級：汽車-超20級、掛車-120。2016年12月-2017年4月日均交通量為9 613輛。

以上行方向主橋變截面連續箱梁(跨徑組合：52 m+80 m+52 m)為監測對象，采用振弦式傳感器進行應變長期監測，監測部位為各孔跨中位置，傳感器布置于箱梁內部側面，距箱梁底20 cm處。

此類振弦式傳感器能夠同時監測溫度與混凝土應變且對結構安全無損，靈敏度及精度較高(±0.1%滿量程)，穩定性較好，耐惡劣環境能力強(工作條件：-20～60 ℃)，適合長期觀測，由于混凝土與傳感器材料熱膨脹系數不同，故需要消除溫度改變引起的誤差。本文采取目前國內最常用的軟件溫度補償法消除該誤差，計算方法為

Δε=K(f12-f02)+Δt1α-Δt2β

(1)

式中：K為傳感器標準系數，由廠家給出；f為頻率；Δt1，Δt2分別為傳感器和混凝土的溫度變化值；α，β分別為振弦和混凝土的線膨脹系數。

2 數據采集結果與分析

2.1 應變-溫度相關性

對2017年8月1-7日，橋各孔跨中單個測點的每日整點監測數據為樣本空間進行分析，各測點應變和溫度隨時間的變化趨勢見圖1。其中應變沿正方向發展表示“混凝土應變增大，混凝土呈現受拉趨勢”；反之沿負方向發展為“混凝土應變減小，混凝土呈現受壓趨勢”。

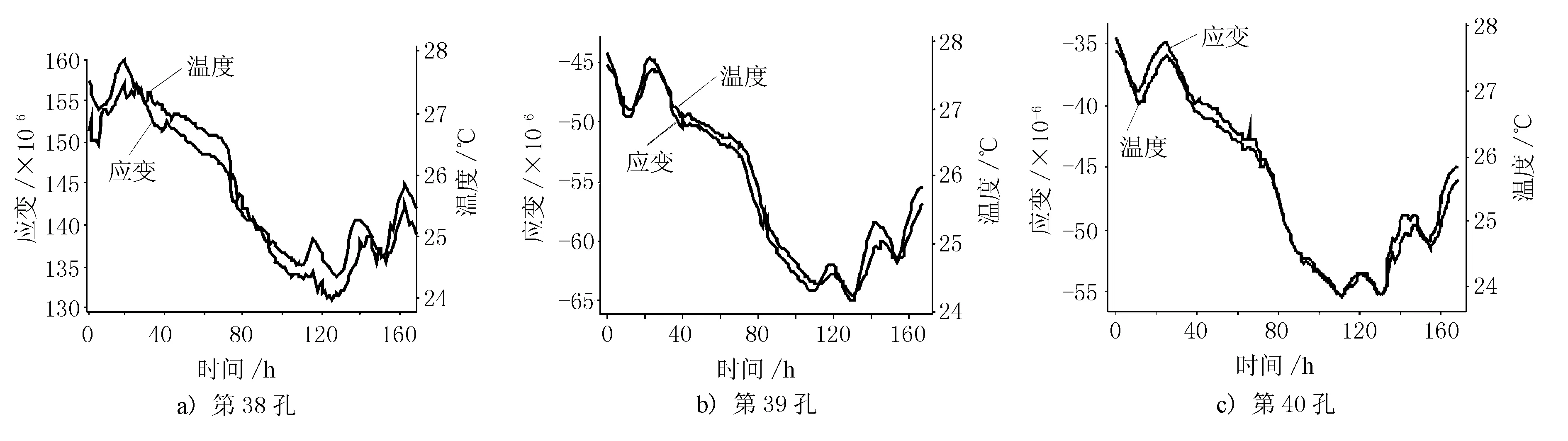
圖1 主橋各孔跨中應變、溫度曲線圖

各測點溫度與應變變化趨勢均為正相關，各測點應變值不同，第38孔跨中下緣混凝土相對于初始值為受拉狀態，其余兩孔跨中下緣混凝土均為為受壓狀態。但變化趨勢也基本一致，均為應變減小，混凝土呈受壓趨勢。

為了明確應變和溫度之間的相關性，按溫度高低繪制各測點溫度-應力散點圖，見圖2。

圖2 主橋各孔跨中應變、溫度散點圖

由圖2可見，應變和溫度之間存在明顯線性相關性，通過計算其線性相關系數R，進一步驗證兩者相關性。溫度-應變相關系數分別為：R38=0.962，R39=0.986，R40=0.997，說明3個測點應變與溫度之間均屬線性正相關，溫度變化是混凝土應變的主要影響因素。

2.2 應變監測值成分分析

根據橋梁結構分析和混凝土應變理論，混凝土橋梁結構某一時刻的混凝土應變主要由3部分組成，可表示為下式

ε總=εt+εL+εR

(2)

式中：εt為溫度應變；εL為荷載應變；εR為收縮徐變應變。

溫度應變包括混凝土與傳感器兩者受溫度變化影響產生的應變。本工程應變測量采用具有溫度自補償功能的振弦式傳感器，故傳感器應變可忽略不計。

荷載應變包括恒荷載應變和可變荷載應變。在結構正常情況下，恒荷載即為橋梁自重，故恒荷載應變為固定值，而可變荷載由于其不確定性，故可變荷載應變為隨機值。本文應變監測系統是在橋梁運營5年后建立，應變監測值是相對于安裝傳感器狀態時的相對值，故可以忽略由恒荷載引起的的混凝土應變。

根據混凝土結構收縮徐變理論，混凝土在第1年內完成75%的收縮徐變，隨后收縮徐變速度以指數速度下降，并在20年后趨于終值。草河口大橋竣工時間為2011年，距今已7年，混凝土收縮徐變速度已經大幅下降，并且數據采集周期相對于收縮徐變周期過短，由混凝土收縮徐變引起的應變變化可忽略不計。

綜上所述，該橋監測系統中應變監測值是混凝土應變溫度效應值與可變荷載作用值疊加而成，將溫度效應值提出后，即可得到可變荷載作用值。

2.3 溫度效應剔除

溫度對混凝土應變的影響雖然較復雜，但總體上可以看作是線性關系和非線性關系的疊加，由前文溫度-應變的R值可知，兩者之間存在很強的正線性相關性，故可以忽略溫度對應變的弱非線性作用，因此采用最小二乘法進行線性回歸，令

ε=a×t+b

(3)

式中：a，b為待定系數。對于樣本值(ti，εi)，使

(4)

的取值最小，即可獲得待定系數a，b的估計值。故再令

(5)

(6)

聯立式(4)、式(5)可得

(7)

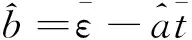
(8)

根據式(7)、式(8)即可求得待定系數a，b的估計值，各測點的應變-溫度回歸方程見表1。

表1 溫度-應變回歸方程

綜上所述，采用應變監測值作為樣本進行線性回歸，能夠正確地反映溫度效應對應變的影響趨勢，通過將應變監測值與回歸方程計算值相減，剔除溫度效應的線性影響，結果見圖3。

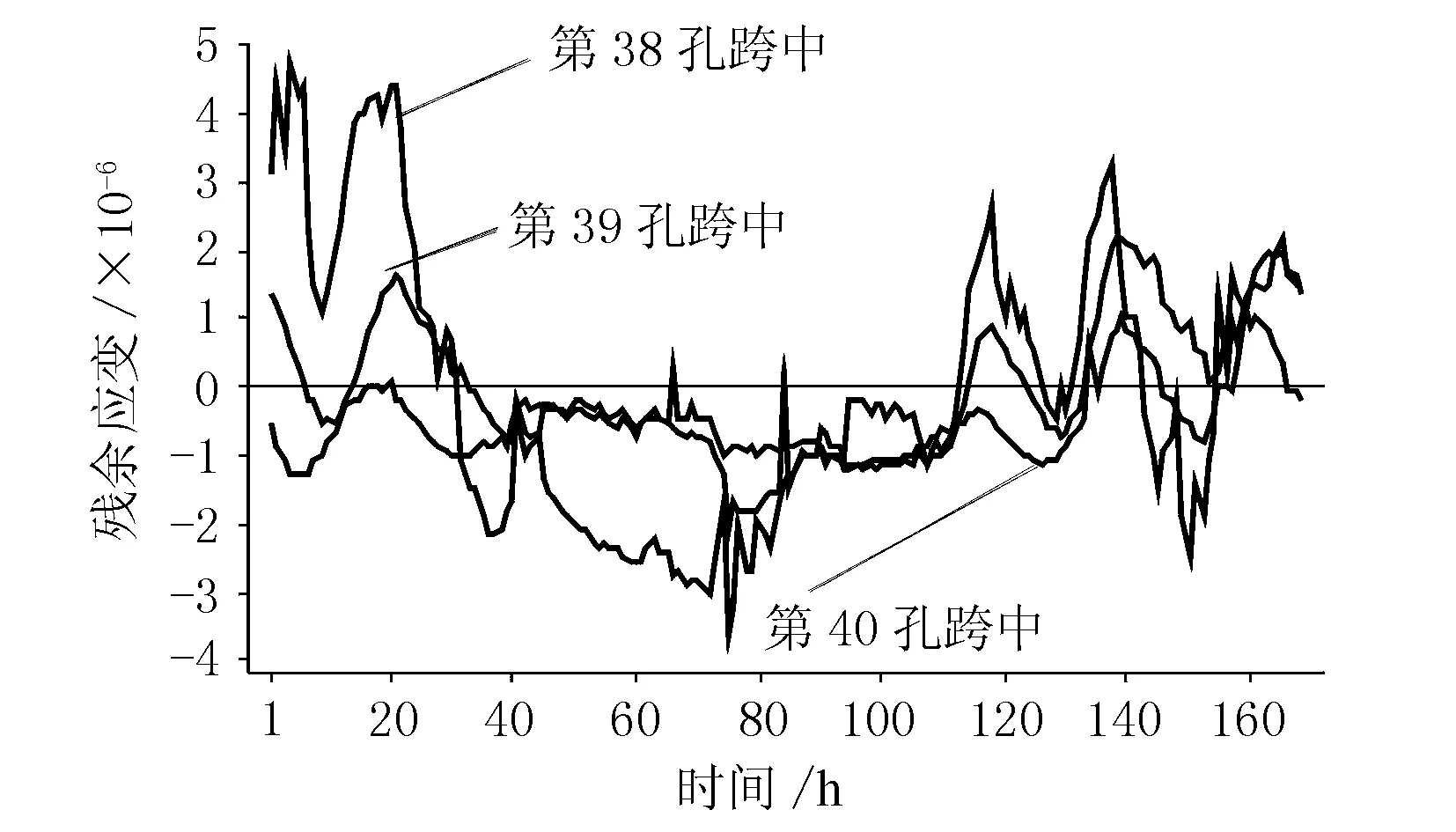
圖3 剔除溫度效應后的應變殘差

由于線性回歸方程忽略了溫度對應變的非線性作用，故余下的應變殘差變化為可變荷載與溫度非線性作用的共同影響，但根據前文所得溫度與應變的線性相關性系數，認為溫度非線性作用影響較小，應變殘差主要受可變荷載作用[5]。從圖中可以看出，各測點應變殘差呈隨機分布，均在坐標軸上下(-4×10-6到5×10-6區間內)來回浮動，第38孔明顯大于其余兩孔，不存在長時間單調性變化。

3 應變殘差的預警閾值設定

實現橋梁安全狀態實時預警是建立橋梁健康監測系統的重要目標，設定分級預警閾值是預警系統的核心內容。過于保守的預警閾值設定，會導致預警系統過于敏感、謊報、多報，浪費不必要的人力物力；閾值設定過松，則不能及時有效地發揮預警作用[6]。設定低級和高級兩級預警閾值，方便監測人員實時觀察，應變值一旦達到低級預警級別時，監測人員可立即發現并分析異常原因，及時采取預防措施，防止混凝土應變向高預警級別發展，從而避免安全事故的發生。

由于應變監測系統的實測值為相對于傳感器安裝時的相對值，無法確定安裝前混凝土已產生的應變值，故對監測總應變進行預警難度較大，不易達到理想的預警效果。在混凝土結構彈性工作階段，可變荷載作用可通過應變值增量反映，不需要確定應變絕對值，且可變荷載作用是運營期橋梁結構安全的主要影響因素，故選擇對應變殘差進行預警。

結合連續箱梁的的結構特點，分析典型病害為跨中下撓過大和箱梁開裂，本工程應變測點布置在3孔跨中靠近箱梁底部的位置，故選擇對混凝土受拉狀態進行預警。

3.1 低級預警

低級預警閾值通過計算數據特征參數分析其變化規律，同時確定一個數據變化常態的安全區間，使我們能夠以比較高的可靠度相信橋梁狀態是安全的，而落在區間外的有理由相信橋梁處于亞健康狀態，即設置基于海量監測數據的低級“異常閾值”。

在橋梁結構健康狀態下，以一段時間內應變殘差的最大統計值為低級預警閾值。當實測應變值與回歸方程計算值的殘差超出閾值，則觸發低級預警。需要注意的是，根據同一測點不同時間段數據獲得的回歸方程會發生變化，為保證所得的應變殘差的準確性，需要通過最新一次采集的溫度與應變數據對預警系統中已有的溫度-應變回歸方程進行更新。

3.2 高級預警

基于荷載試驗時應變監測變化量設定高級預警閾值。2017年7月對該橋進行了荷載試驗，采用單輛重約350 kN的三軸載重的車列模擬可變荷載進行加載，試驗結果表明：各孔正彎矩截面底板應變校驗系數與撓度校驗系數均在規范常值之內，但各孔截面都存在個別應變校驗系數超過規范常值的現象，說明混凝土強度滿足設計要求，但材料老化，強度降低；相對應變殘差與相對殘余變形均在規范限值(20%)之內，說明結構處于彈性狀態。

各孔以最不利工況加載時,應變增量監測結果見圖4。

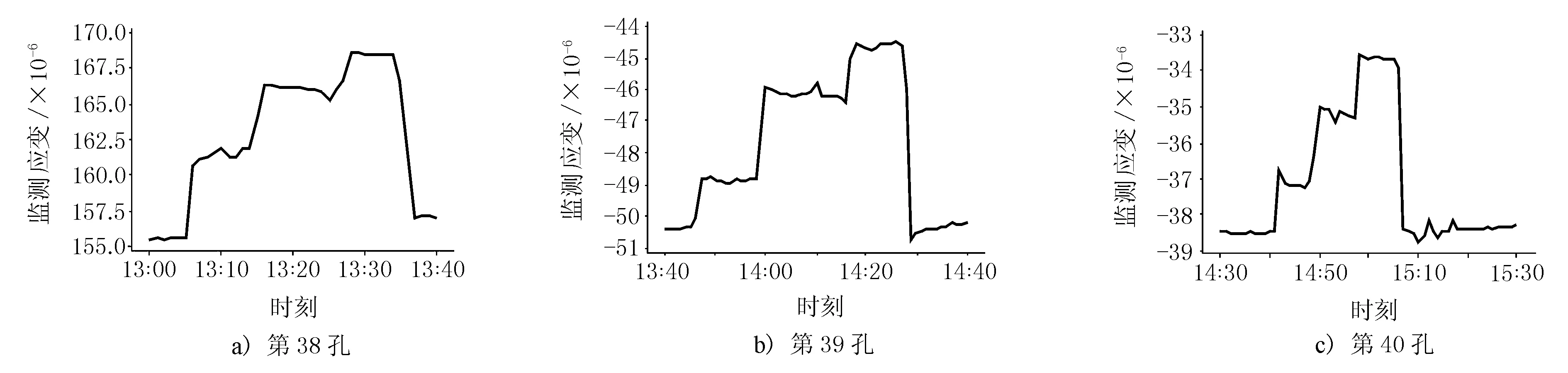
圖4 荷載試驗應變監測結果

由圖4可見，跨中下緣混凝土應變增大，呈受拉趨勢，三級加載效果明顯，且卸載后應變值迅速恢復至加載前狀態。其中第38孔應變變化值明顯大于其余兩孔，與前文的應變殘差分布情況一致，原因可能為梁體剛度降低或預應力損失。由于各工況加載持續時間較短，期間溫度變化較小，故可近似認為應變監測值變化完全由加載車輛作用引起。

高級預警閾值的設定：采用荷載試驗各孔最大正彎矩工況加載時應變監測變化值作為高級預警閾值。當應變殘差超出高級預警閾值時，則認為可變荷載達到設計活載或混凝土結構超出彈性工作階段，需密切關注橋梁安全狀態。

3.3 預警結果

根據上述預警閾值的設定方法，以2017年8月1-7日監測數據與荷載試驗時監測數據為基礎，設置的兩級預警閾值見表2。

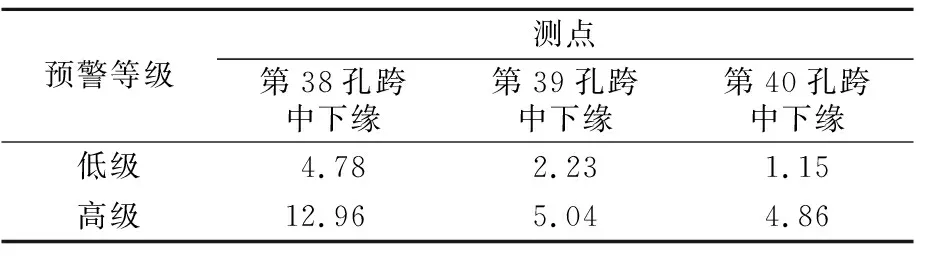
表2 應變殘差預警閾值 ×10-6

以主跨第39孔為例，對2017年8月8-9日應變殘差進行預警，結果見圖5。

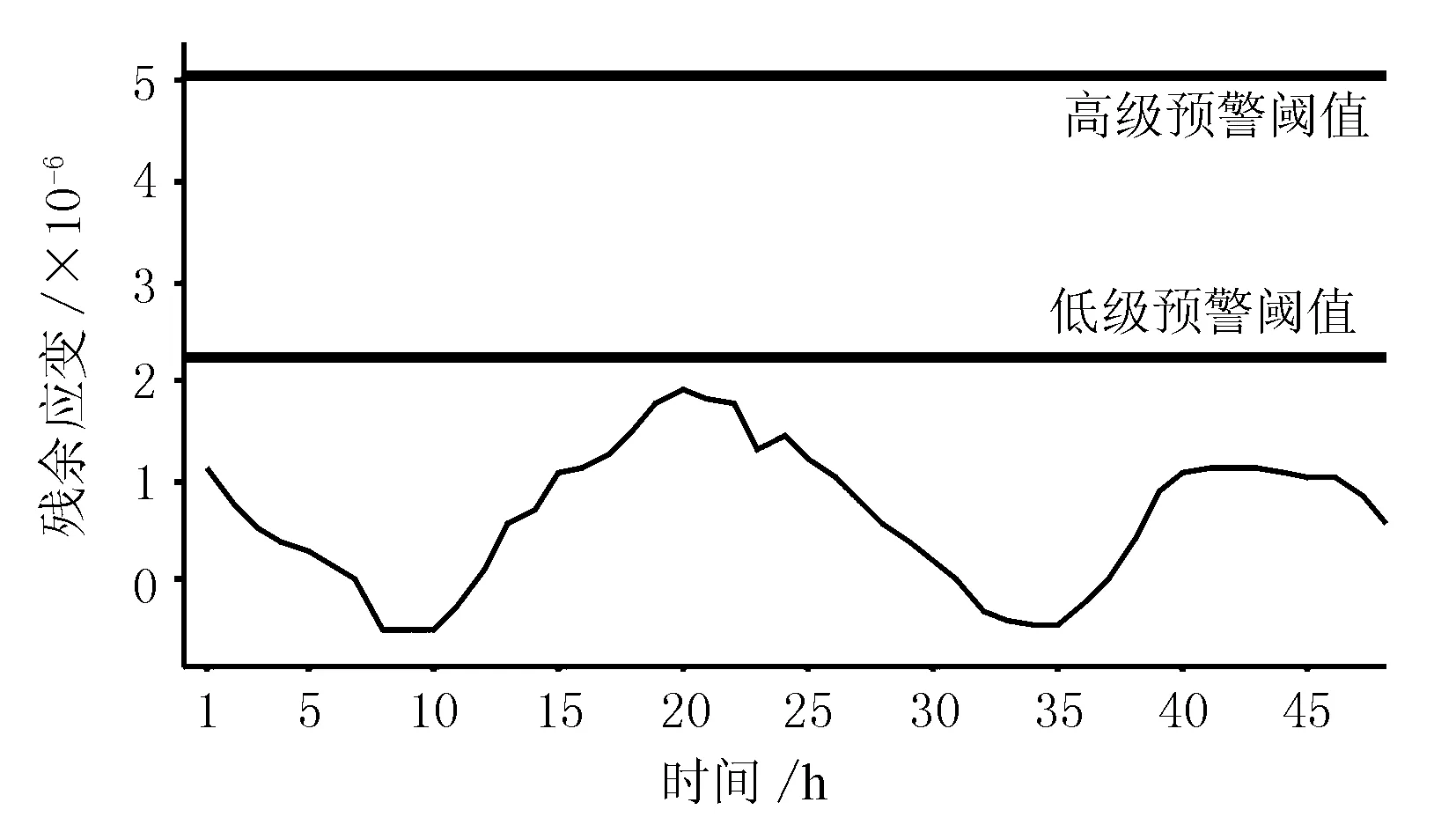
圖5 應變殘差預警結果

由圖5可見，應變殘差值與變化趨勢符合規律，未超過低級預警閾值。

4 結論

1) 溫度是混凝土應變的主要影響因素，兩者屬于線性強相關，通過線性回歸能夠提取應變監測中的溫度效應值。

2) 結構正常時，可變荷載作用產生的應變殘差隨機分布在0值附近，無長期單調性變化。采用一定時間內應變殘差的最不利統計值和荷載試驗最不利工況下監測應變變化值設置的低、高級預警閾值，能夠達到預期的預警效果。

3) 在預警過程中，需要通過后續采集的溫度與應變數據對溫度效應回歸方程進行實時更新，保證回歸方程及應變殘差值的可靠性。