基于雙變量單向函數的門限可變秘密共享方案

黃科華，陳和風

?

基于雙變量單向函數的門限可變秘密共享方案

黃科華1，陳和風2

（1. 泉州幼兒師范高等專科學校 初等教育系，福建 泉州 362000；2. 集美大學 計算機工程學院，福建 廈門 361021）

利用雙變量單向函數和拉格朗日插值公式構造了一個門限秘密共享方案，該方案可以按照事先預定的門限來進行秘密共享（門限可變），不需要使用到安全信道，用戶的份額不會暴露，可以多次使用，是一個完美的秘密共享方案。

門限可變秘密共享方案；雙變量函數；拉格朗日插值公式

1 研究背景

為安全起見，銀行保險柜的鑰匙不能由一個人單獨保存，必須由多個人，每個人掌握一部分鑰匙。當足夠多的人集中在一起的時候，才能打開保險柜。解決類似問題的方案我們稱之為秘密共享方案（，）。一個秘密共享方案由以下幾個部分組成：：可信中心或者密鑰分發者：合成密鑰參與者集合、密鑰集合、準入結構（由可合成密鑰的集合組成）、分配算法和合成算法。

(,)門限秘密共享方案是比較流行的秘密共享方案，它指的是個參與者中，個或者大于個成員合作可以合成密鑰，而少于個人合作得不到密鑰的任何信息的秘密共享方案。Shamir和Blakley于1979年分別獨立提出了基于拉格朗日插值公式和線性集合投影方法的(,)門限秘密共享方案[1,2]。此后有一些研究者對方案進行了改進[3-6]。這些方案都存在著一些不足之處，如：（1）需要使用到安全信道來傳輸密鑰份額；（2）份額只能使用一次，如果要合成新密鑰，還需重新再次發送份額；（3）準入結構較為單一，確定完就無法改變等。針對這些不足，有的研究者提出了多秘密共享方案[7-8]、可驗證秘密共享方案[9]、加權秘密共享方案等[10]。

在解密之前，有可能需要對門限值進行改變，如系統安全等級升高或者下降、成員的份額泄露或者信任度降低等。Laih等人于1989年首次提出了門限可變秘密共享概念并給出了相應方案[11]。此后，一些研究者陸續利用插值公式[12]、基于格等技術[13]，構造門限可變秘密共享方案。本文在這些方案的基礎上，提出了一個基于雙變量單向函數的門限可變秘密共享方案。

2 預備知識

2.1 陷門單向函數

陷門單向函數可以選擇RSA函數等。

2.2 雙變量單向函數

函數(,)稱為雙變量單向函數，其滿足以下條件：

（1）對于確定的,，可容易計算=(,)；

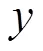
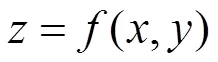
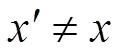
文獻[14]證明了雙變量單向函數的存在，并在()（為大素數）上提供了一種利用一對一hash函數的構造方法。

2.3 完美秘密共享方案

3 基于雙變量單向函數的門限可變秘密共享方案

以下方案皆在()（為大素數）上進行討論。假設密鑰分發者要把個密鑰

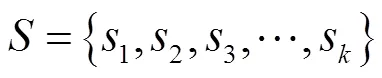
分享給個成員

3.1 密鑰的分發階段

（5）分發者選擇個多項式

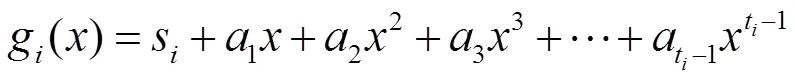
3.2 密鑰的合成階段

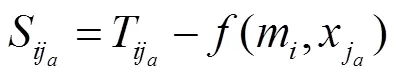
4 對本方案的分析

4.1 門限可變

4.2 不需要安全信道

4.3 成員的私鑰可以重復利用

4.4 該方案是一個完美的秘密共享方案

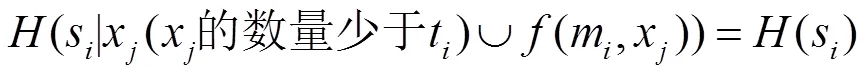
5 結語

引入雙變量單向函數構造了一個可變門限的秘密共享方案，該方案可以按照事先預定門限來進行秘密共享（門限可變）；不需要使用到安全信道；密鑰合成后，用戶份額不會暴露，可以多次使用；該方案是一個完美秘密共享方案。

[1] Shamir A. How to share a secret[J]. Communications of the ACM, 1979, (11): 612-613.

[2] Blakley G R. Safeguarding cryptographic keys[A]. Proceedings of the National Computer Conference[C]. US: American Federation of Information Procession Societies, 1979: 242-268.

[3] Asmuth C, Bloom J. A modular approach to key safeguarding[J]. IEEE Transactions on Information Theory, 1983, (2): 208-210.

[4] Mignotte M. How to share a secret[A]. Proceedings of the Workshop on Crytography[C]. Burg Feuerstein, Germany, 1983: 371-375.

[5] Karnin E, Greene J, Hellman M. On secret sharing systems[J]. IEEE Transactions on Information Theory, 1983, 29(1): 35-41.

[6] Brickell E F, Davenport D M. On the classification of ideal secret sharing schemes[J]. Journal of Cryptology, 1991, (2): 123-134.

[7] He J, Dawson E. Multistage secret sharing based on one-way function[J]. Electronics Letters, 1994, 30(19): 1591-1592.

[8] Yang C, Chang T, Hwang M. A (t, n) multi-secret sharing scheme[J]. Applied Mathematics and Computation, 2004, 151(2): 483-490.

[9] Chor B, Goldwasser S, Micali S. Verifiable secret sharing and achieving simulataneity in the presence of faults[A]. 26th Annual Symposium on Foundations of Computer Science[C]. Portland, USA, 1985: 383-395.

[10] S Iftene, I Boureanu. Weighted threshold secret sharing based on the Chinese remainder theorem[J]. Scientific Annals of the “Al. I. Cuza” University of Iasi, Computer Science Section, 2005.

[11] Laih C-S, Harn L, Lee J-Y, et al. Dynamic threshold scheme based on the definition of cross-product in an n-dimensional linear space[J]. Journal of Information Science and Engineering, 1991, 7(1): 13-23.

[12] Zhifang Zhang, Yeow Meng Chee, San Ling, et al. Threshold changeable secret sharing schemes revisited [J]. Theoretical Computer Science, 2011: 418.

[13] Ron Steinfeld, Josef Pieprzyk, Huaxiong Wang. Lattice-based threshold-changeability for standard CRT secret-sharing schemes[J]. Finite Fields and Their Applications, 2005:12(4)35-36.

[14] He J, Dawsom E. Multisecret-sharing scheme based on one-way function[J]. Electronics Letters, 1995, 31(2): 93-95.

Threshold Changeable Secret Sharing Schemes Based on Two-Variable One-Way Function

HUANG Ke-hua1, CHEN He-feng2

(1. Department of Primary Education, Quanzhou Preschool Education College, Quanzhou362000, China; 2. Computer Engineering College, Jimei University, Xiamen361021, China)

By using two-variable one-way function and Lagrange interpolation formula, we create a perfect threshold secret sharing scheme which is able to share secret according to the set threshold (which means it’s changable) for many times, while not using secure channels or revealing users’ shares.

Threshold Changeable Secret Sharing Schemes; Two-variable One-way Function; Lagrange interpolation formula

O1-0

A

1009-9115(2018)06-0041-03

10.3969/j.issn.1009-9115.2018.06.009

福建省自然科學基金項目（2017J01761），廈門市科技局平臺補助金項目（B16145）

2018-05-07

2018-09-21

黃科華（1983-），男，福建泉州人，碩士，副教授，研究方向為密碼學、信息安全。

（責任編輯、校對：趙光峰）