基于CATIA二次開發的直升機燃油重心計算及應用

蔣 輝，趙 輝，王 慶

（中國直升機設計研究所，江西 景德鎮333001）

直升機的重心位置直接影響著飛行性能和操縱使用安全，直升機的重心包線是直升機在飛行使用中不可逾越的一道安全線，如果裝載不當會造成重心位置超出重心包線范圍，可能會造成機毀人亡的慘劇[1-3]，而直升機各部件、系統、設備、乘員、旅客、貨物、武器、燃/滑油的重量重心位置，都將影響到直升機全機的重心，因此，在總體布置和安排時，應全面考慮和綜合安排，使得直升機在各種使用任務狀態下，其重心不得超出重心包線的范圍[4]。

作為直升機基本系統之一的燃油系統，其燃油的消耗以及在載油不滿的油箱中燃油所處姿態和位置（由于飛機姿態和加速度），都對直升機重心有較大影響[5]。由于燃油重心大幅變化所帶來的飛行不穩定，一方面，將增加飛行操縱的負擔，另一方面也將降低直升機的飛行品質，影響飛行任務的執行。因此，正確計算燃油重心的變化是確定飛機重心變化的重要依據[6]。

目前在燃油重心的計算方法上，已有不少的研究機構和學者提出了多種研究方法，包括切片法[7-9]、SPH 法[10-11]、ALE 法[12]以及 VOF 法[13]等等。基于切片法的燃油重心計算，可以較快地獲得飛行器在穩態飛行過程中的燃油重心，是飛行器型號工程設計過程中比較常用的一種方法。而基于SPH法、ALE法以及VOF方法的燃油重心計算，則主要是利用有限元的方法來進行仿真計算，這三種方法可以在考慮油面晃動的情況下，對燃油重心進行短時瞬態的分析，分析精確較高，但其僅適用于時間歷程較短的仿真計算，在做長時間歷程（比如基于飛行剖面時間歷程）進行分析時，計算量較大，計算耗時較長。

在直升機型號設計過程中，往往是根據不同飛行任務，以特定的燃油量來計算全機的重心，很少考慮因直升機飛行狀態的不同，而導致的燃油重心變化，進而帶來對全機重心的影響。本文將基于直升機的飛行剖面數據，考慮燃油液面的變化，對CATIA Automation API宏進行二次開發，采用切片計算與尋優分析相結合的方式，對某型直升機的燃油重心進行自動計算，并對燃油重心在全機重心評估中的應用進行簡要介紹。

1 基于CATIA Automation API宏二次開發的燃油重心計算

CATIA的Automation API（自動化應用接口）提供了交互的方式，可通過錄制宏（自動生成VBScript等）或Visual Basic平臺等方式實現用戶所需功能。該應用接口的模型設計功能比較全面，并具備了與任何OLE（對象連接與嵌入技術）所兼容的平臺進行通信能力[14]。

1.1 燃油體及油平面

為便于燃油重心的計算，需要將油箱的燃油存儲空間封閉為一個幾何實體，即燃油體。以某型直升機為例，其燃油體如圖1所示。

圖1 燃油體模型

不同燃油量下的燃油體重心計算，應當首先確定出燃油的液面狀態。雖然在直升機的飛行過程中，油箱內的燃油處于時時晃動的狀態，燃油液面呈現出不規則的復雜曲面形狀，但是對處于穩態飛行姿態下的燃油油面，工程上常常忽略燃油液面的復雜波動而把油面簡化成平面來看待，即油平面，并經驗證，這種簡化能夠滿足解決工程問題的需要[9，15]。

根據相關文獻[7，16]所述，油平面方程可表示為：

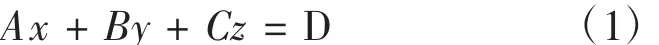
式中：A、B和C不同時為零，D為常數項。

由于油平面的法向向量N=（A，B，C）與過載向量n=（nx，ny，nz）的方向相同，其中nx、ny和nz分別為機體坐標系下X、Y、Z三個方向的過載分量[5]。因此，可以通過在CATIA中構建垂直于過載向量n=（nx，ny，nz）的切割平面來切割燃油體。油平面如圖2所示。

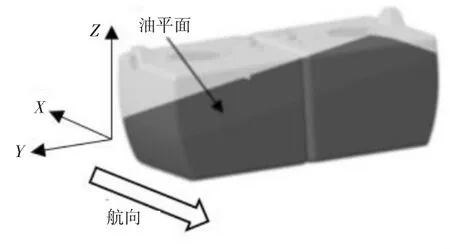
圖2 油平面

1.2 基于Automation API宏的燃油重心計算

基于Automation API宏的燃油重心計算，可按圖3所示流程進行。

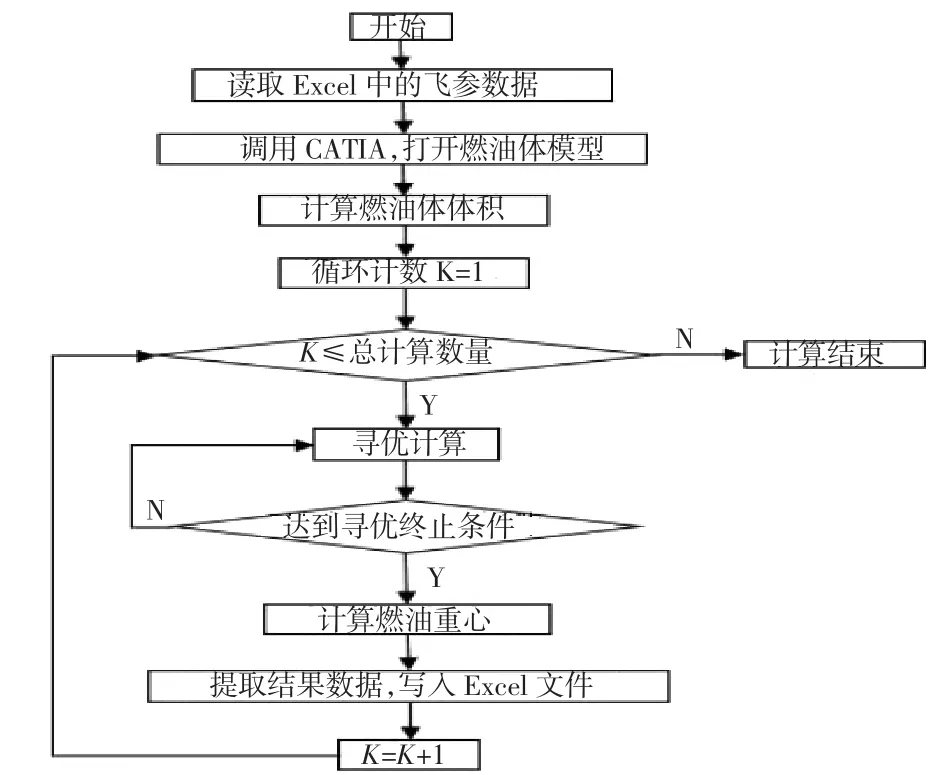
圖3 燃油重心計算流程

1.2.1 飛行剖面數據讀取

飛行剖面是指為完成某一特定飛行任務而繪制的飛機航跡圖形，它由若干飛行狀態組成，對于直升機而言，它包括滑行、起飛、垂直爬升、巡航、懸停、下滑、垂直著陸等飛行狀態[17]。飛行剖面是飛行器戰術技術要求的組成部分和重要設計依據，也是形象地表達飛行任務的一種形式[18]。飛行器的飛行剖面示意圖如圖4所示。

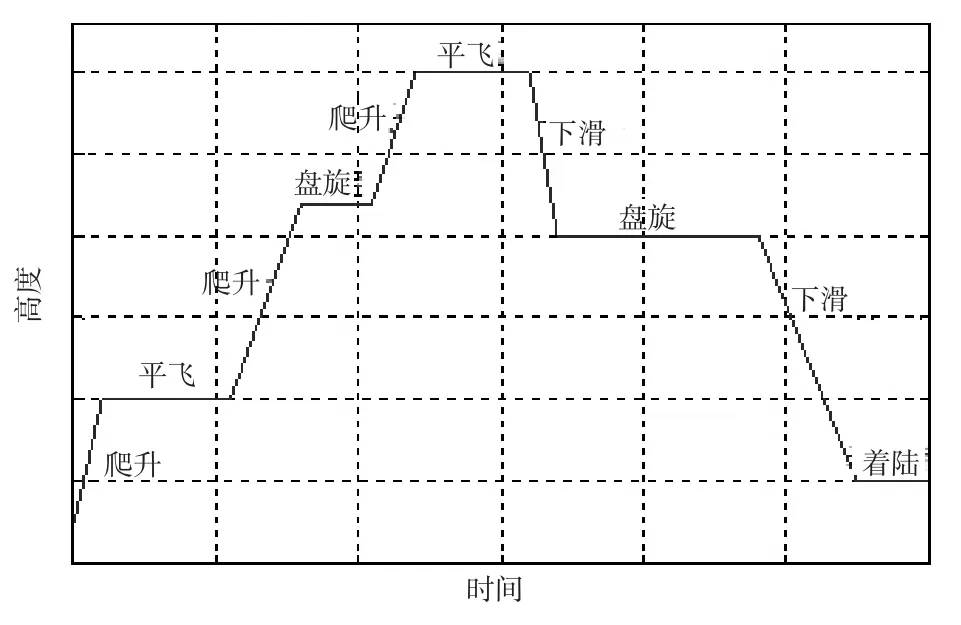
圖4 飛行器的飛行剖面示意圖

根據某型直升機的飛行剖面數據，計算出了該型直升機在不同飛行狀態下三個方向的過載系數和剩余燃油量。表1中給出了部分飛行狀態下的過載系數及剩余油量。

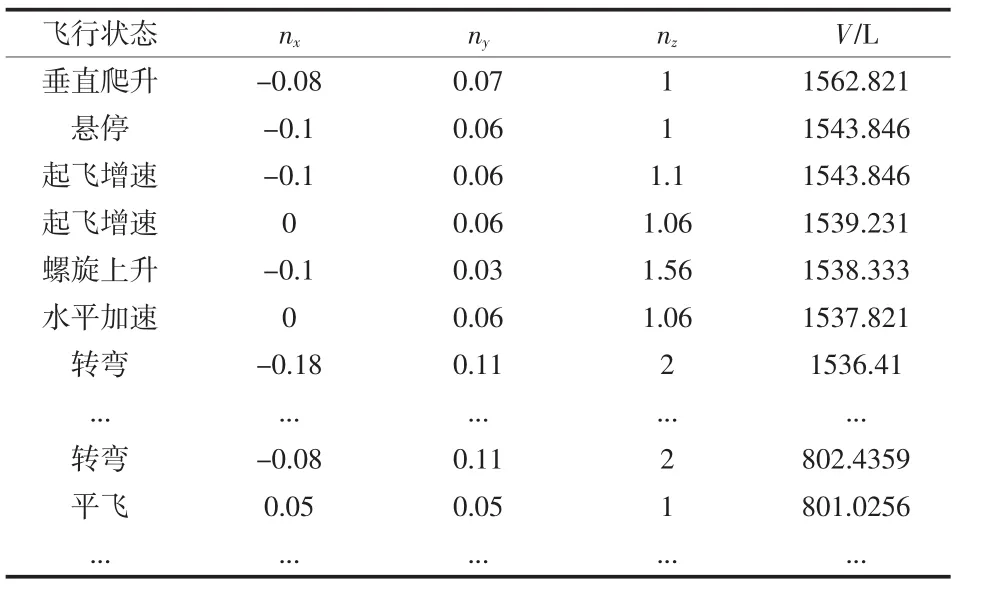
表1 過載系數及剩余油量

表1中的V為燃油箱中的剩余燃油量。

在進行燃油重心計算前，首先需要讓CATIA能自動讀取并存儲包含有各飛行狀態下過載系數及剩余燃油量的EXCEL數據，對應的CATIA宏流程如圖5所示。

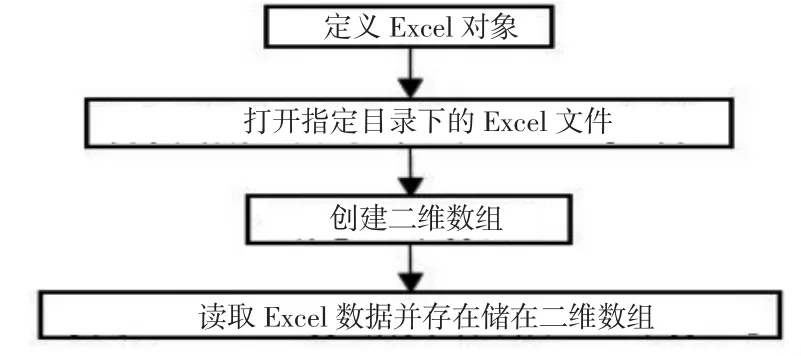
圖5 飛行狀態數據讀取流程圖

1.2.2 燃油體模型讀取

在讀取飛行狀態數據后，需要由CATIA打開指定目錄下的燃油體模型。

所要打開的燃油體模型中，除了有燃油體之外，還包括有以坐標原點和任意初始點（x0，y0，z0）所創建的直線段，以及垂直于該直線段且通過點（x0，y0，z0）的切割平面。在后續的計算中，點（x0，y0，z0）中的三個坐標值將由點（nx，ny，nz）所代替，則直線段可轉變為過載向量的方向線，而切割平面也將平行于油平面。

1.2.3 燃油體的體積計算

為便于后續計算，需要提前定義燃油體的體積參數T，并計算當前燃油體的體積。對應的宏關鍵語句如式（2）和（3）所示：

//定義體積參數“T”

1.2.4 油量尋優計算

由于是要在給定的剩余燃油量的條件下，對燃油體進行切割，以便切割后的燃油量與表1中所給定的剩余燃油量相同，或者數值上極為接近。為此，需要采用尋優方法，以表1中的剩余燃油量V為尋優目標，以切割平面到原點的距離“L”為尋優變量，進行尋優計算，可建立尋優函數如式（4）所示。

式中，fL為尋優函數，T為每次切割計算后的燃油體體積。

當改變L值使得fL取得最小值時，即min（fL）值最接近于0時，可以認為T近似等于V，則尋優結束，并計算此時燃油體的重心。

在CATIA中，常見的可供使用的尋優方法有模擬退火算法（Simulated Annealing，SA）和共軛梯度算法（Gradient Algorithm）。其中模擬退火算法的思想最早是由N.Metropolis等人于1953年提出的[19]，該算法本質上屬于蒙特卡洛方法，它的每次迭代必須進行多次目標函數計算，因而在處理實際問題時計算效率不高，且存在著最優解被忽略的可能性[20]。

共軛梯度算法最早是由Hestenes和Stiefle提出來的[21]，并由Fletcher和Reeves推廣到求解非線性優化問題[22]，是介于最速下降法與牛頓法之間的一個方法，它僅需利用一階導數信息，不但克服了最速下降法收斂慢的缺點，還避免了牛頓法需要存儲和計算Hessse矩陣并求逆的缺點，是求解大型線性和非線性方程組最有效的方法之一。

共軛梯度法的原理是在尋優過程中，利用當前點xk處的梯度向量g（xk）和前一迭代點xk-1處的搜索方向dk-1對最速下降方向進行如下修正：

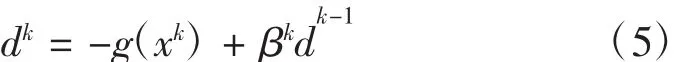
并保證新的搜索方向dk與之前的搜索方向dk-1，dk-2，...，d0之間滿足共軛關系。而其中修正系數βk的不同又進一步形成了不同的共軛梯度法[23]。

在CATIA中采用共軛梯度算法進行尋優，需要分別設置尋優目的類別、尋優算法、尋優變量的上下限、尋優迭代終止的判據等四項關鍵參數。

對于尋優函數式（4），需要在每一個飛行狀態點下尋找其最小值，因此，設置尋優目的類別為尋找最小值，即：

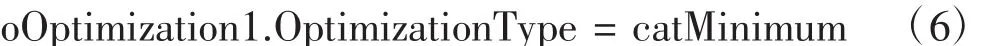
設置尋優算法為共軛梯度法：

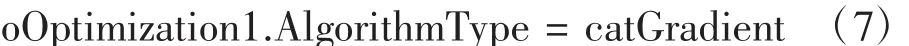
如前所述，需要設置切割平面到原點的距離L為尋優變量，考慮到該型直升機燃油箱模型的實際情況，可設置L的上下限分別為2000和0，即：

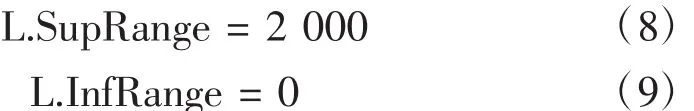
為保證在尋優精度已能滿足實際需要的情況下，亦即fL值非常接近于0時，CATIA能夠停止當前飛行狀態下的尋優計算而進入到下一個飛行狀態的尋優計算，可設置單次尋優的最大迭代次數為500次或者設置最長尋優時間為5分鐘，即：

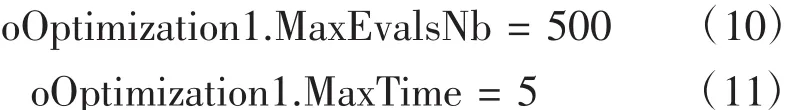
1.2.5 燃油重心計算

經尋優計算后，所得到的被切割后的燃油體體積可以認為等于飛行剖面數據中所給定的剩余燃油體積V，此時便可以通過（12）~（17）這6條關鍵語句來獲得燃油體在X和Y方向上的重心。

//建立當前燃油體的參考“oRef”

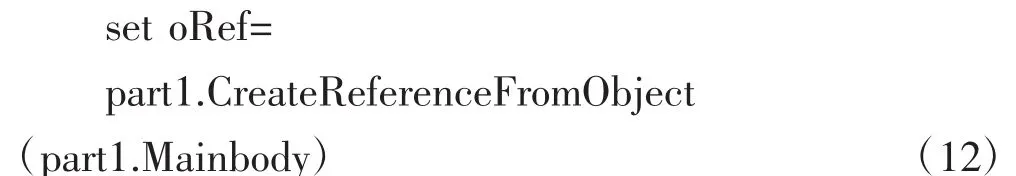
//獲取當前工作臺的空間分析模塊“SPAWorkbench”

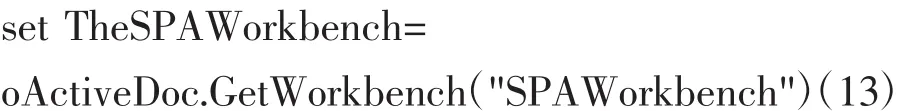
//獲取參考“oRef”的可測量對象

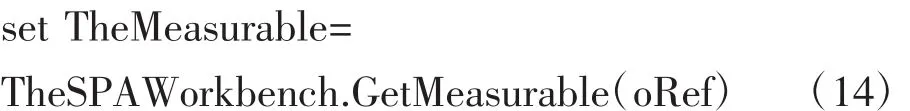
//獲取參考“oRef”可測量對象中的重心坐標

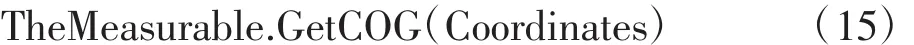
//將重心坐標的x和y值分別賦予Gx和Gy

其中Gx和Gy即為燃油體在X和Y方向上的重心。

由于飛行器在Z方向的重心變化往往較小，且對飛行器的性能影響不大，通常不作Z方向的重心計算。

1.2.6 計算結果輸出與分析

通過前面對函數fL以及重心的計算，可得到各飛行狀態下fL、X方向重心和Y方向重心變化曲線如圖6~圖8所示。

從圖6中可以看出，通過尋優計算所得到的每一個飛行狀態點下的fL值，即切割后的燃油量T與所給定的剩余燃油量V的差值均在10-5量級左右，已足夠小，表明切割后的燃油量可以近似等于所給定的剩余燃油量，此時的燃油體可以用于對重心的計算。

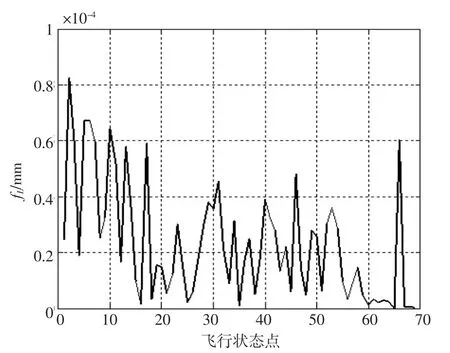
圖6 fL的變化曲線圖

從圖7中給出的X方向重心變化曲線圖中可以得到，在整個飛行剖面中，直升機的燃油在X方向的重心變化范圍為：9 807.219 mm~9 914.871 mm，變化幅度為107.653 mm.

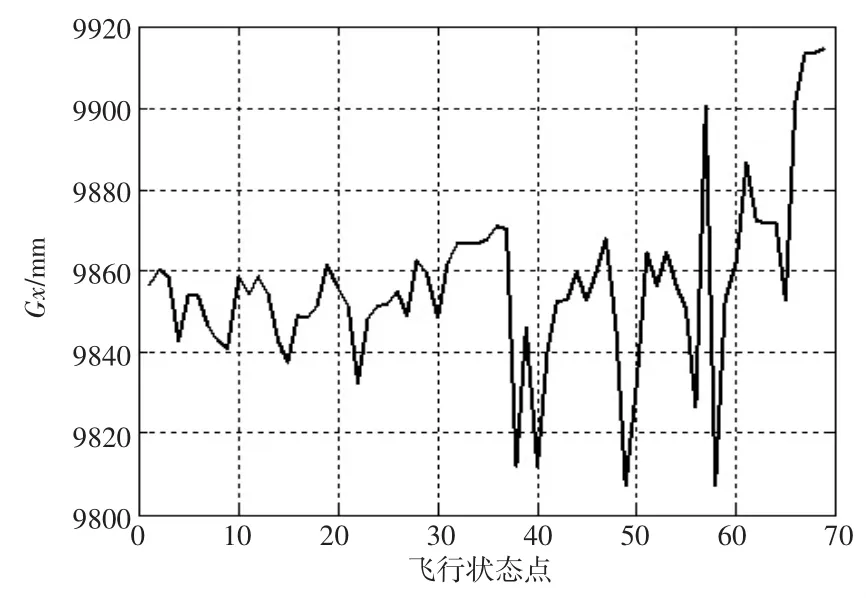
圖7 X方向重心變化曲線

其中，X方向上的重心最小值Gx=9 807.219 mm，出現在第49個飛行狀態點處，此時對應的飛行狀態為水平加速。

X方向上的重心最大值Gx=9 914.871 mm，出現在第69個飛行狀態點處，此時對應的飛行狀態為垂直著陸。

從圖8所給出的Y方向重心變化曲線圖中可以得到，在整個飛行剖面中，直升機的燃油在Y方向上的重心點大致交替地位于機身左右兩側，且更大幅度地偏向于機身左側，即-Y方向。整個Y方向上的重心變化范圍為：-197.68 mm~58.545 mm，變化幅度為256.225 mm.

Y方向上的重心最小值Gy=-197.68 mm，出現在第69個飛行狀態點處，此時對應的飛行狀態為垂直著陸。

Y方向上的重心最大值Gy=58.545 mm，出現在第58個飛行狀態點處，此時對應的飛行狀態為水平減速。

此外，可以發現，該型直升機在整個飛行剖面中，Y方向上的重心變化范圍約為X方向上的重心變化范圍的2倍，即燃油在機身橫向上的重心變化范圍約為縱向重心變化范圍的2倍，這不僅與整個飛行剖面中的飛行狀態有關，也與燃油箱的橫向尺度約為縱向尺度的2倍有關。

2 燃油重心在全機重心評估中的應用

如前所述，燃油重心應當滿足全機重心的要求。根據直升機的飛行剖面，其各飛行狀態下的全機重心坐標可以表示為[5]：

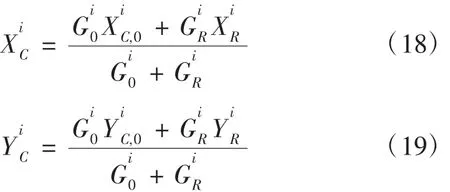
結合各飛行狀態下的燃油重量，通過將圖7和圖8中的燃油重心數據帶入式（18）和式（19），可以計算出各飛行狀態下的全機重心坐標，并與全機重心包線圖進行比較，當且僅當各飛行狀態下的重心位置均位于全機重心包線內時（如圖9和圖10所示），才能滿足直升機對重心的使用要求。

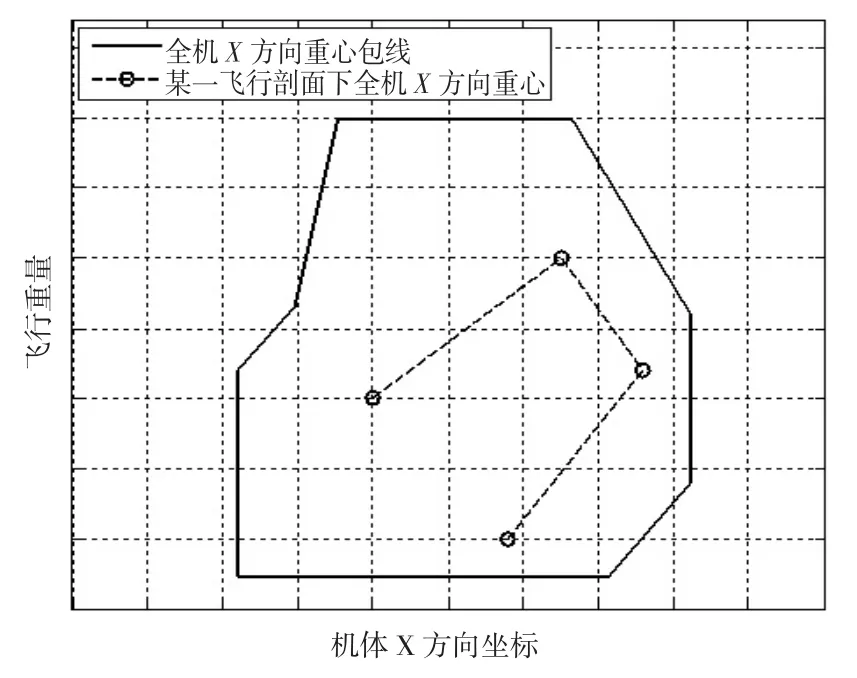
圖9 X方向重心包線示意圖

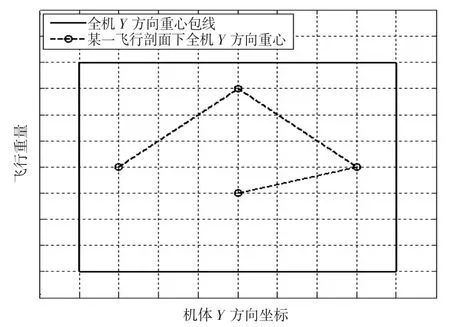
圖10 Y方向重心包線示意圖

如果所計算出的燃油重心使得全機的重心超出了重心包線范圍，就至少需要從以下幾個方面來考慮對燃油系統進行設計改進：

（1）更改燃油箱的幾何外形，以改善燃油在燃油箱中的分布情況；

（2）對于大型燃油箱，可以通過在燃油箱內增加擋板或者將大燃油箱更改為若干個小燃油箱，減少因為燃油在燃油箱中大尺度范圍內的晃動而導致重心的劇烈變化；

（3）重新調整燃油箱在直升機上的安裝位置；

（4）增設轉輸系統和引射系統，對各燃油箱里的燃油量進行主動分配和調整；

（5）調整相鄰燃油箱之間的高連通孔位置，或者在低連通孔處增設重力單向活門，通過控制燃油在各燃油箱中的躥流方向，達到控制燃油重心的目的。

通過以上幾個方面對燃油系統進行改進設計后，需要重新根據飛行剖面再次計算燃油重心以及全機重心，經多輪迭代，直至能夠滿足全機重心的要求。

3 總結

（1）以某型直升機燃油箱為研究基礎，提出了基于飛行剖面數據，考慮不同過載系數下燃油液面的變化，來對燃油重心進行計算，并以此對全機重心進行評估的思路；

（2）對CATIA Automation API宏進行了二次開發，采用切片計算與尋優分析相結合的方式，對燃油重心進行了自動計算，得到了對應于該型直升機飛行剖面中各飛行狀態下的燃油重心變化曲線圖，并發現，在該飛行剖面下，燃油在機身橫向上的重心變化范圍約為縱向重心變化范圍的2倍；

（3）給出并解釋了基于CATIA Automation API宏二次開發的燃油體積計算、尋優設置以及重心計算的部分關鍵語句；

（4）對所獲得的燃油重心在全機重心評估中的應用進行了介紹。