基于磁場FE和CFD的磁流變阻尼器力學性能分析

劉昕運 吳大林 馬吉勝

(1.陸軍工程大學火炮工程系， 石家莊 050001； 2.西京大學機械工程學院， 西安 710123)

0 引言

磁流變(MR)阻尼器的內部通常填充有特殊的磁流變液體，該液體由非導電液體、微小的鐵磁性粉末和少量添加劑混合而成[1]。這種特殊的流體在磁場作用下表現出粘塑性非牛頓流體的特性[2]。流體的屈服應力由磁感應強度決定，即為磁流變阻尼器的阻尼力可控的原因[3]。相比于膠質阻尼器和其他阻尼器[4-5]，MR阻尼器的滯回環范圍更大[6]。目前，MR阻尼器發展迅速，已在車輛工程[7-8]、土木工程[9]、醫療器械[10]、飛行器[11]和武器工業[12]等領域被廣泛使用。

隨著計算機技術的發展，有限元分析(Finite element analysis，FEA)和計算流體動力學(Computational fluid dynamics，CFD)仿真技術已成為分析磁流變液體和磁流變阻尼器的主要手段。與傳統的一維解析模型相比，FEA和CFD數值模擬更加準確，且能夠獲得更多可視化參數[13]。文獻[14]在COMSOL中耦合了磁場和流體，并進行了實驗和仿真。文獻[15-16]在ANSYS/CFX中用CLL語言耦合了磁流變阻尼器模型。文獻[17]模擬了磁流變阻尼器的磁場分布，并考慮了溫度的影響。以上研究屬于邊界已知的“顯式”主動運動問題，而本文研究的沖擊運動屬于邊界條件不可知的“隱式”被動運動問題。目前，此類問題在國內外尚未見相關研究和報道。

本文提出單向耦合數值模擬方法。首先在COMSOL中對磁場進行有限元分析，然后將磁場結果導入Fluent中，結合Six DOF模型和UDF文件對沖擊過程進行分析，通過實驗進行驗證，以期準確獲取磁流變阻尼器的力學特性。

1 數值模型

1.1 結構原理

圖1 磁流變阻尼器CAD設計圖Fig.1 CAD design of MR damper

近年來，磁流變阻尼器出現了多種結構，單出桿式[18]和雙出桿式[19]，有氣體腔[20]和無氣體腔[21]，特殊式[22]等。本文涉及的MR阻尼器用于緩沖艦炮系統中的高速運動的實驗彈，CAD設計如圖1所示。由于外部幾何限制，對阻尼器結構進行了特殊設計，如圖2所示，主要由活塞桿、磁流體活塞、空氣彈簧活塞、缸體、限位塊、線圈、壓縮空氣、磁流變液組成。活塞桿兩端直徑相等，彈性回復力主要來自空氣壓縮。活塞中繞有兩組線圈，其被外殼密封。導線從活塞桿內部通過并連接外部直流電源。當線圈通電時，將產生大致如圖2所示的磁場分布。磁場導致磁流變液中的鐵磁固體顆粒按磁感線形成鏈狀，導致環形間隙中的部分流體表現出極大的屈服應力，流體通過間隙時會產生較大的阻尼力。阻尼器主要尺寸如表1所示。

1.2 靜磁場FE模型

有限元模型在多物理場仿真軟件COMSOL/Multiphysics中建立。依據麥克斯韋方程組[10]計算電磁場，包括恒定電荷密度的連續性方程、安培定律和法拉第定律，即

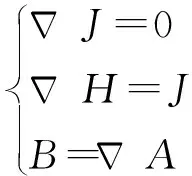
(1)

其中

B=μoμrH

(2)

式中H——磁場強度

J——電流密度

A——磁矢量勢

B——磁通密度

μr、μo——材料磁導率、真空磁導率

根據阻尼器的對稱性，生成二維軸對稱網格，如圖3所示。計算域總共有70 375個四邊形網格單元。為了評估網格的相關性，生成另一組更加細密的網格，共281 500個四邊形單元。比較兩組網格的磁通強度計算結果，輸出曲線幾乎相同。這說明生成的網格已經非常精細，結果誤差與網格尺寸基本無關。

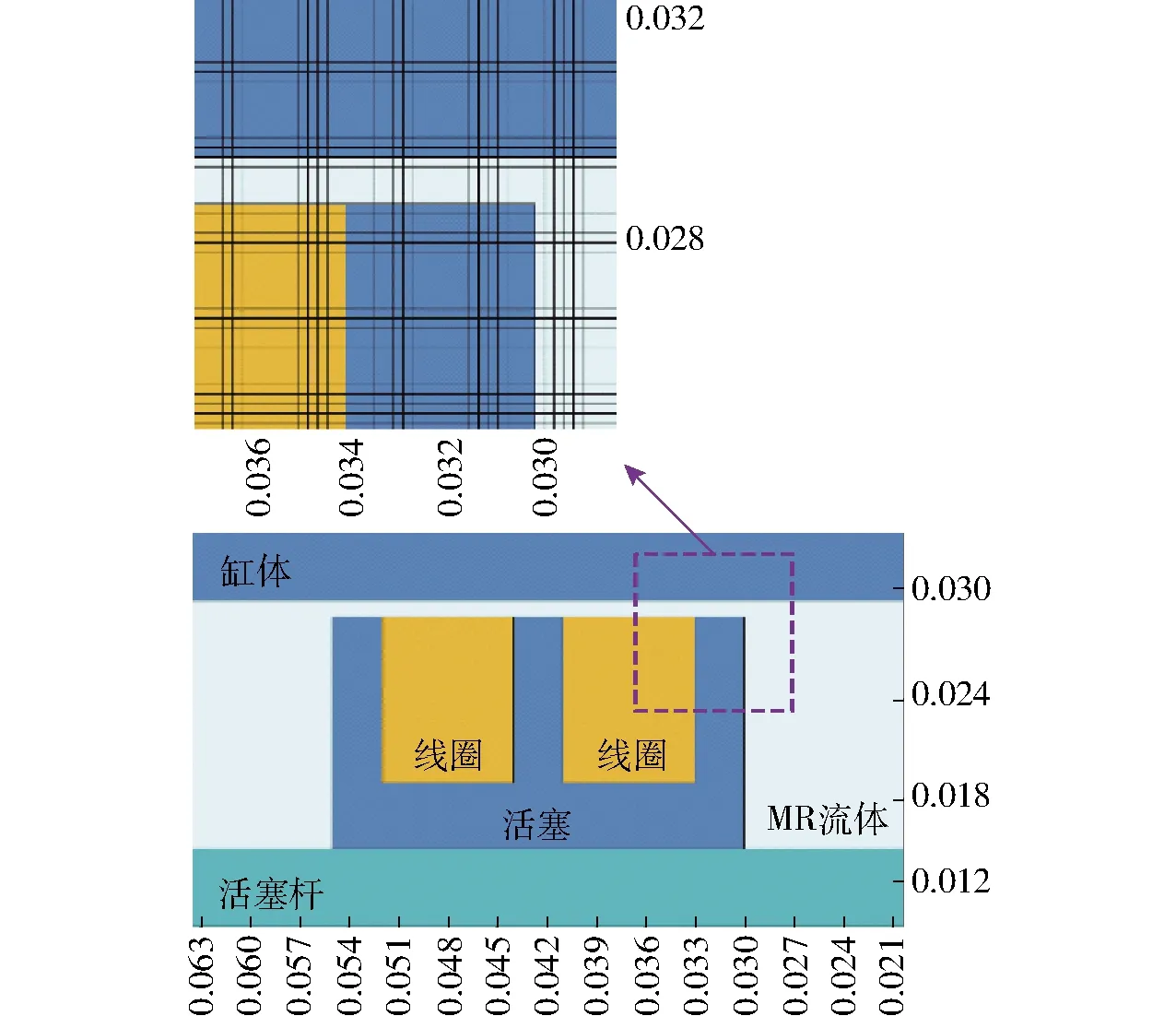
圖3 磁流變阻尼器的有限元網格Fig.3 FE mesh of MR damper

采用LORD公司的MRF-140CG型磁流變液，圖4為該磁流變液的特性曲線。活塞頭和缸體采用碳素結構鋼1045，活塞桿采用低磁導率金屬。線圈導線采用美國線規AWG 24標準銅線。部分材料參數如表2所示。

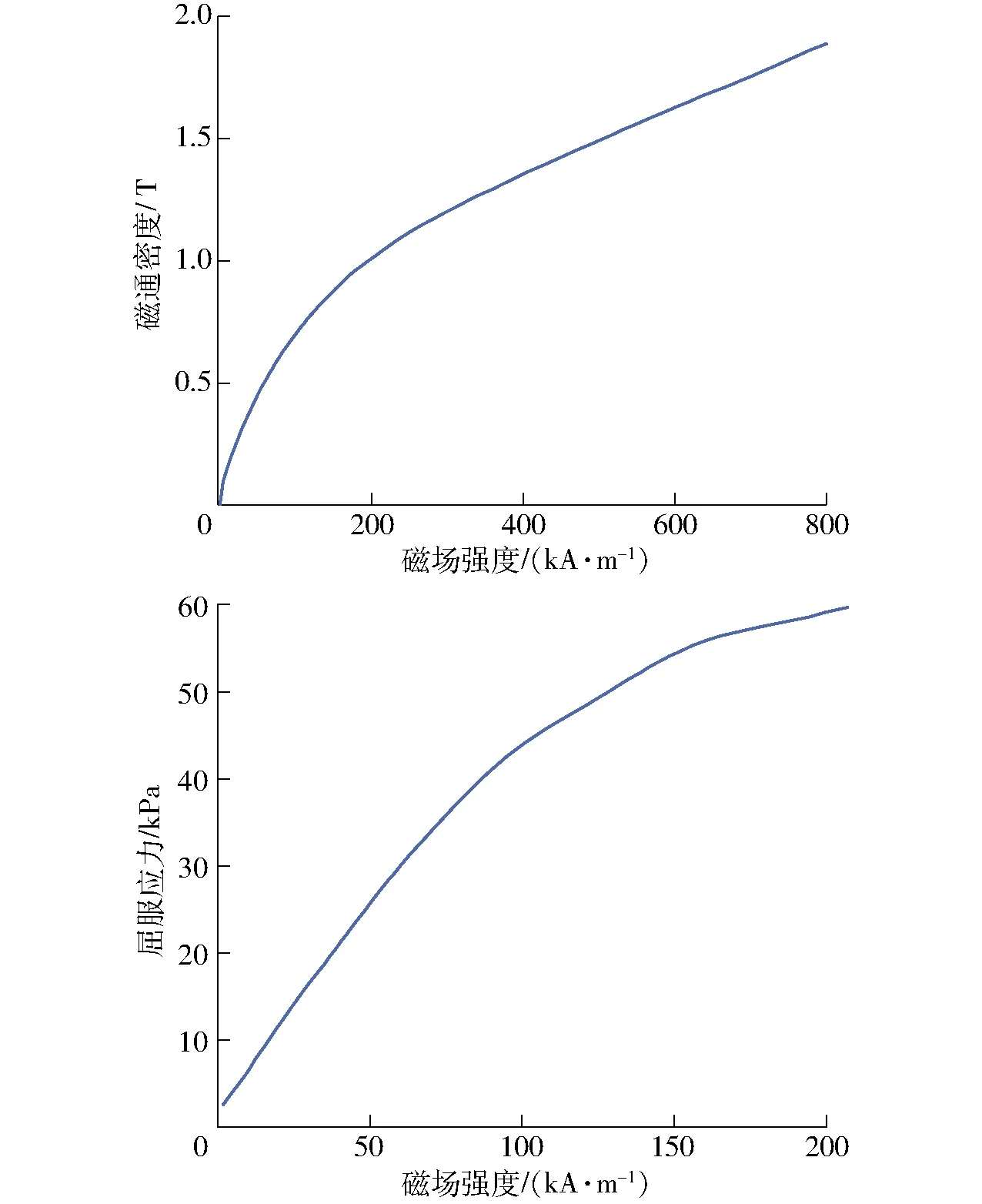
圖4 MRF-140CG型磁流變液的特性曲線Fig.4 Characteristics of MRF-140CG MR fluid

1.3 磁流變液CFD模型

MR阻尼器的CFD分析需考慮湍流和能量傳遞，其中流體控制方程包括連續性方程、Navier-Stokes方程和能量方程[23]

表2 材料屬性參數Tab.2 Material property parameters

(3)

式中ρ——流體密度V——流體速度

fb——體積力p——差壓

μ——動力粘度h——比焓

λ——熱導率Φ——粘性耗散項

Sh——源項T——溫度

1.3.1流體本構模型

根據圖4中磁流變液材料屬性定義磁通密度B和屈服應力τy的關系曲線。使用Hill sigmoidal函數擬合為

(4)

式中，ε=117 024.8，β=0.967 66，k=1.693 63。

目前，針對粘塑性流體提出了多種本構模型[24-26]。本文采用由雙曲正切函數定義的流變粘度模型[13-14]，即

(5)

式中α——粘度增長控制因子，取0.03

ζ——粘度增長控制因子，取0.1

對速度沖擊過程進行CFD分析時，必須考慮MR流體的可壓縮性。因為阻尼器在沖擊瞬間壓力變化非常大，如果不考慮流體的壓縮性將導致壓力計算出現異常。液體壓力用Tait狀態方程描述，即

(6)

式中m——密度指數ρ0——參考密度

E0——參考體積模量

1.3.2空氣彈簧

磁流變阻尼器有空氣彈簧結構，空氣腔存在一定初始壓力，其主要作用是提供回復力，使被壓縮的阻尼器自動復位。空氣彈簧力Fs一般依據氣體多變過程方程來描述，即

(7)

式中p0——初始壓力，取2.5 MPa

Aair——活塞面積，取1 756.15 mm2

W0——初始體積，取52 684.5 mm3

n——氣體多變指數，取1.3

x——活塞位移

1.3.3流體網格定義

流體計算域仍然采用二維軸對稱四邊形網格。動網格使用Layering層鋪技術，網格被壓縮至一定程度時，貼近壁面的網格會坍縮與合并。而網格被拉伸至一定程度時，貼近壁面的網格會分裂出新層。為了順利實現網格層鋪法，在生成網格時需考慮Mesh Interface。如圖5所示，活塞兩側的壁面被定義為剛體移動壁面。僅生成流體域網格，間隙處的網格被加密，總共包含了95 403個四邊形單元。

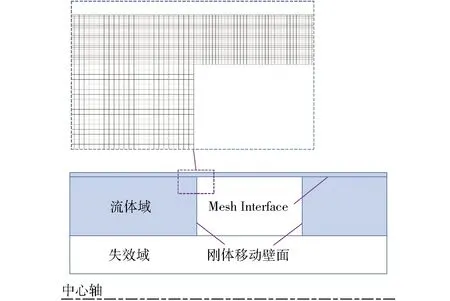
圖5 流體網格定義示意圖Fig.5 Schematic of fluid mesh definition

1.3.4用戶自定義函數

磁流變阻尼器的活塞移動時，磁場的影響區域會跟著變化。所以，對于非牛頓區域的跟蹤和捕捉是必要的。與顯式邊界模型不同，隱式邊界模型的“磁場作用區域”不能直接定義，其需要依賴移動壁面的實時坐標。因此，基于C語言編寫了用戶自定義函數(UDF文件)，并在求解器中進行編譯。

使用“DEFINE_PROPERTY”宏定義計算域的動力粘度屬性。首先，使用“Get_Domain”宏和“Lookup_Thread”宏獲取移動壁面的指針，在此之上用“F_CENTROID”宏訪問移動壁面的坐標信息并存入數組；然后寫入式(4)、(5)和磁場FE分析得到的磁通密度。以上函數中涉及2個變量，其中坐標信息從數組中提取，剪切速率由“C_STRAIN_ RATE_MAG”宏訪問得到；最后用“C_ CENTROID”宏訪問計算域的所有網格單元，并把非牛頓粘度函數賦值于受磁場影響的單元。

活塞只在x方向移動，而且存在空氣彈簧力和限位塊，故還需要定義6自由度模塊的UDF文件。根據頭文件six_dof.h，使用“DEFINE_SDOF_PROPERTIES”宏定義剛體屬性，代碼可以與屬性宏編寫到一個文件中。使用“SDOF_MASS”宏定義剛體的質量，其值取阻尼器負載的質量；使用“SDOFO_1DOF_T_P”宏定義自由度為1個平移自由度；使用“SDOFO_LOC， SDOFO_MIN，SDOFO_MAX”宏定義剛體的位移限制；最后用“SDOF_LOAD_F_X”宏寫入空氣彈簧力式(7)。

2 數值結果

對于單向耦合模型，式(4)、(5)是耦合磁場FEA和CFD的關鍵。通過靜磁場分析得到磁通密度B在流體域的分布，然后將其轉換為動力粘度在流體域的分布，并導入CFD模型。

2.1 靜磁場FE分析

當輸入電流I=4.0 A時，計算域內的磁通密度等值線如圖6所示。大部分磁感線從活塞的兩端穿過流體進入阻尼器的缸體，由于流體和活塞桿的磁導率都非常低，磁通量更多地分布在磁性材料中。輸出環形間隙中間線上的磁通密度分布曲線如圖7所示，磁通密度存在兩個峰值，分別在環形間隙的兩端，最大值達到1.96 T。而在兩個峰值的中部以及外側，磁通密度迅速降低至接近0。

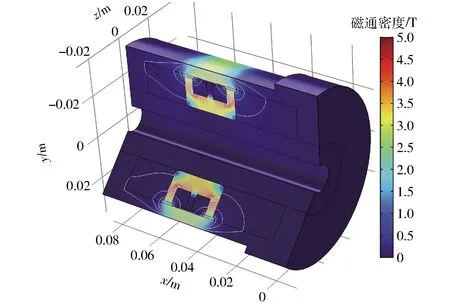
圖6 流體域中的磁通密度分布Fig.6 Magnetic flux density distribution in computational domain

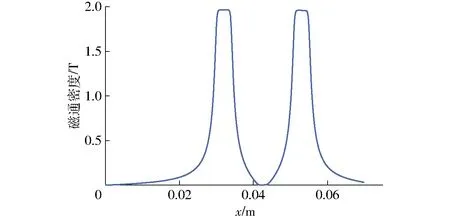
圖7 環形間隙中線上的磁通密度分布Fig.7 Magnetic flux density distribution on middle line of annular gap

2.2 模型驗證

模型采用瞬態壓力基求解器(PBS)。使用Realizablek-ε模型，激活能量方程和粘性熱。設置Coupled算法并采用二階離散格式，求解控制Courant數為50，最大求解時間步長為1×10-5s。

磁通強度在流體中的主要作用區域如圖8所示。受磁場影響的主要區域不全在環形間隙中，間隙的兩端存在溢出。可能會影響阻尼器的力學特性計算結果。因此，在UDF代碼中編寫環形間隙兩端的“圓弧”區域，其結合圖7的磁通密度分布曲線能夠更準確地描述非牛頓粘度。

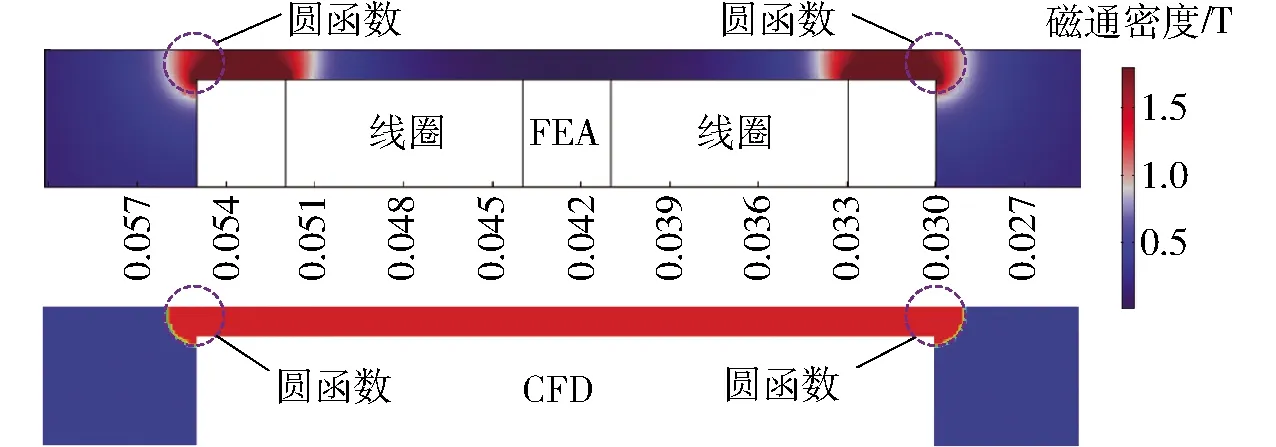
圖8 環形間隙兩端的圓函數區Fig.8 Circular function area at both ends of annular gap

在CSS-55100型萬能試驗機上對阻尼器進行勻速準靜態運動實驗，如圖9所示。固定缸體，對活塞桿進行勻速的加載和卸載。利用壓力傳感器和位移傳感器采集阻力和位移。圖10、11分別為勻速準靜態運動的阻抗力-時間曲線和滯回曲線。對比阻尼器的實驗和仿真曲線，驗證了模型的準確性。

圖9 勻速準靜態實驗設備Fig.9 Uniform quasi-static experimental equipment

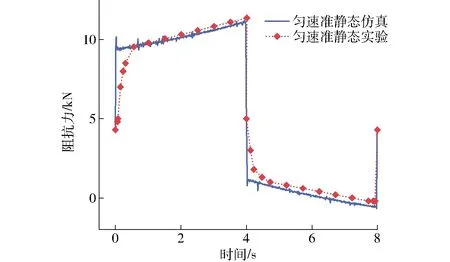
圖10 勻速準靜態運動的阻抗力-時間曲線Fig.10 Resistance-time curves of uniform quasi-static motion

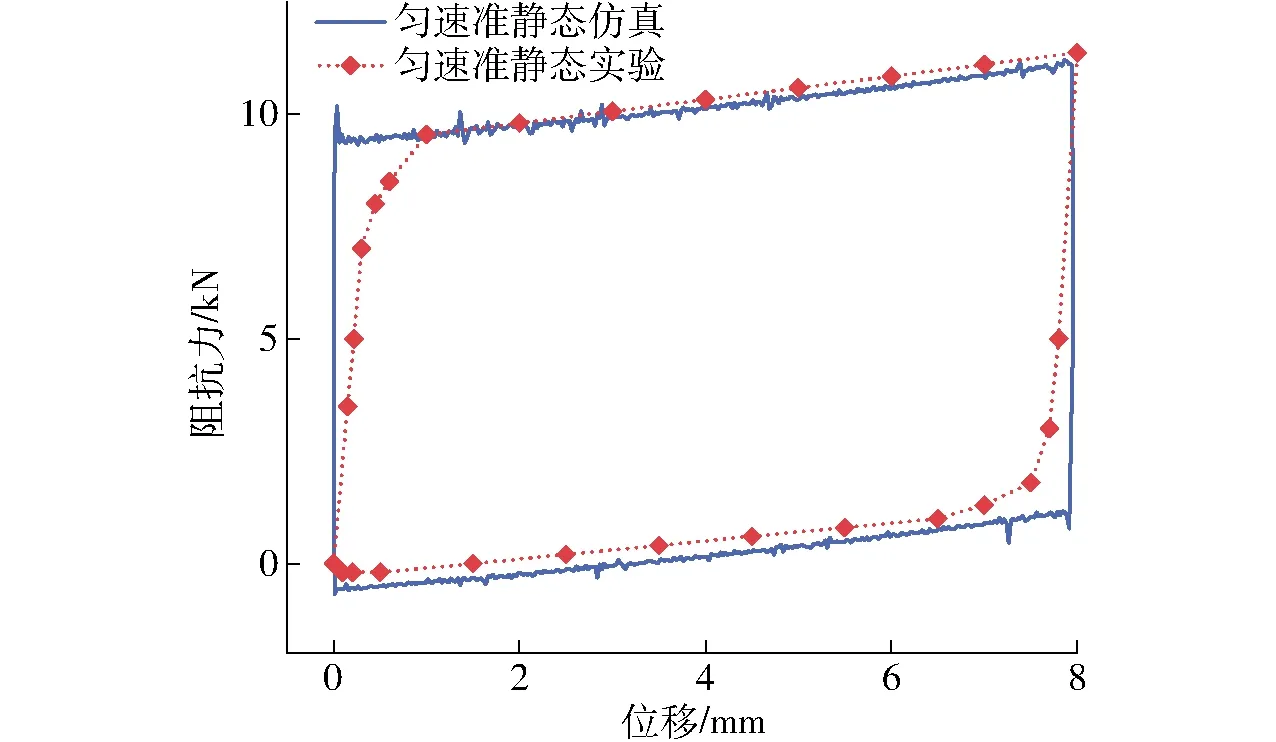
圖11 勻速準靜態運動的滯回曲線Fig.11 Hysteresis loop of uniform quasi-static motion

2.3 沖擊CFD分析

當剛體初速度為7.4 m/s，壁面邊界的運動狀態由流固雙向耦合的6自由度模塊自動解算，總仿真時間為80 ms時，整個沖擊過程的等值線和流線圖如圖12所示。沖擊初期，流體在環形間隙中瞬時最大速度達到了75 m/s以上，但隨著動能的耗散，流體速度會很快降低，達到最大位移僅需4 ms。磁流變阻尼器在運動過程中，流體產生了許多不停變化的渦，且流線極為不規則。但較大的渦都出現在活塞運動方向的后面。

阻尼器吸收的動能主要轉化為流體熱能。由于液體具有粘性，內部摩擦將產生熱量，初始溫度為300 K時，流體溫度分布如圖13所示。高溫液體主要產生于環形間隙，因為此處剪切速率和動力粘度最大。沖擊運動結束時溫度分布并不均勻，活塞一側的平均溫度暫時高于另一側。

輸出的磁流變阻尼器運動學特性曲線如圖14所示。MR阻尼器的壓縮過程持續4 ms，拉伸過程持續大約70 ms。圖14a顯示，MR阻尼器最終無法完全復位，在位移為1.3 mm處幾乎停止運動，這是由Bingham流體性質決定的。阻尼器在復原運動時，流體域的剪切速率逐漸降低。由式(5)可知，在剪切速率很低時，表觀粘度會逐漸大幅升高，從而導致流體剪切應力變大。而隨著位移行程的減小，空氣彈簧力逐漸降低。當空氣彈簧力小于流體阻力時，活塞開始減速直到停止運動。阻尼器在復原運動階段先加速后減速的特征如圖14b所示。在實際應用中，這種現象并不會影響磁流體阻尼器的使用。

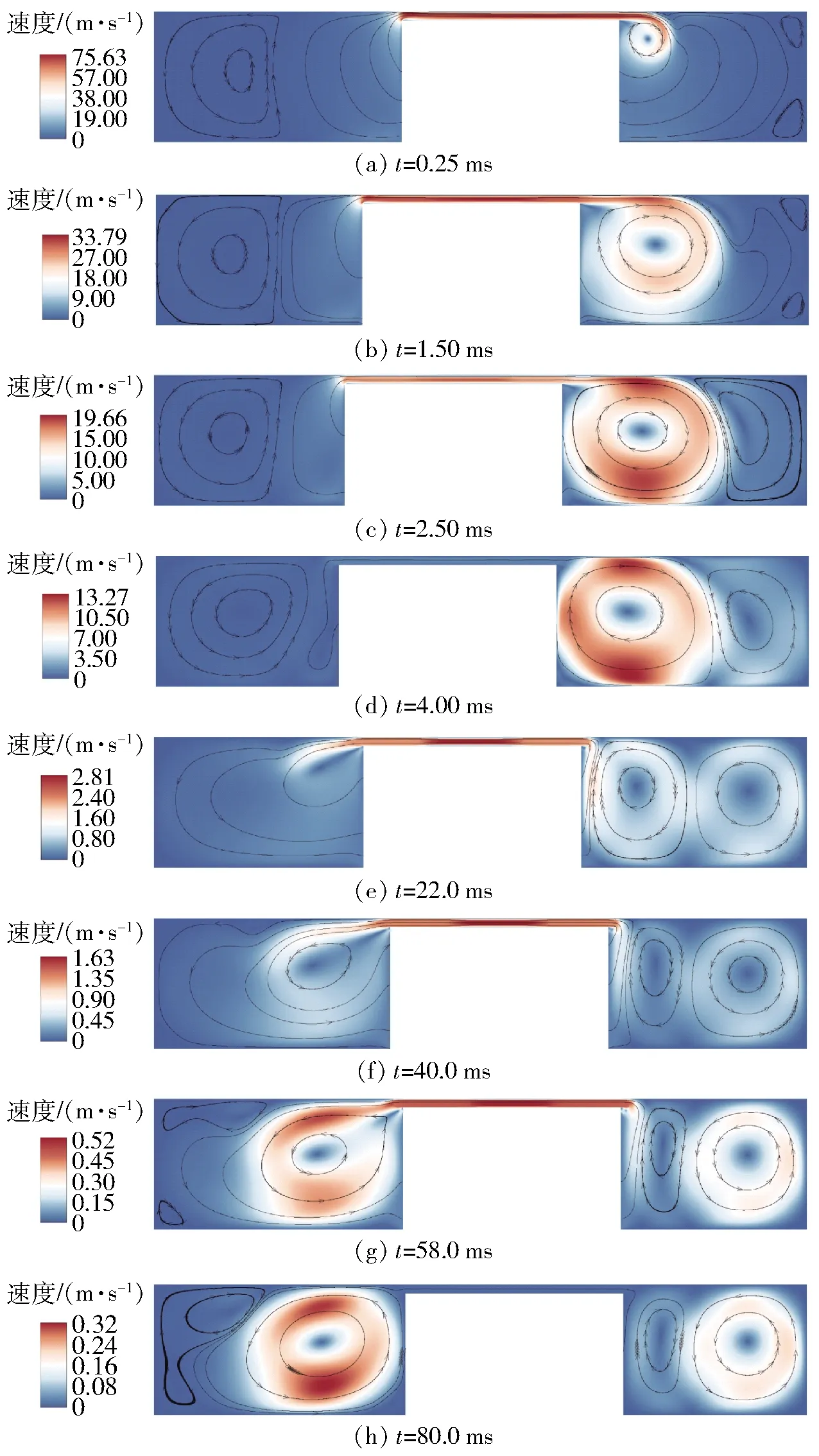
圖12 磁流變阻尼器速度等值線和流線Fig.12 Velocity contours and streamtraces of MR damper

圖13 磁流變阻尼器溫度等值線Fig.13 Temperature contours of MR damper

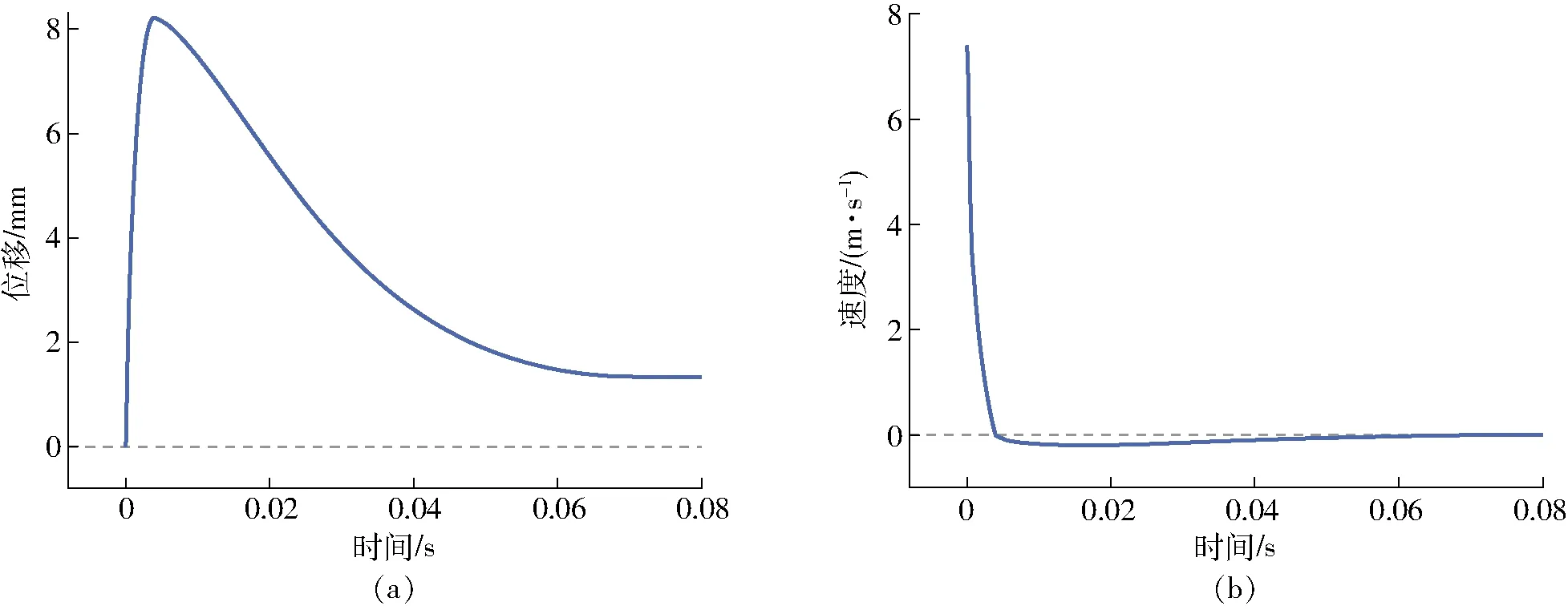
圖14 沖擊運動的運動學特性曲線Fig.14 Kinematic characteristic of impact motion

這是由于當控制電源斷開后，磁流變液會恢復牛頓流體特性，阻尼器將很快完全復位。圖15為沖擊運動的滯回曲線，阻尼器的阻抗力曲線變化非常不規則，最大阻抗力出現在沖擊初期，在行程2 mm處達到最大阻抗力110 kN，而后迅速降低并逐漸趨于平穩。復原階段中的阻抗力保持在200～400 N極低的水平。該磁流體阻尼器在沖擊過程中幾乎吸收了所有的初始動能，其緩沖效能較為優異。

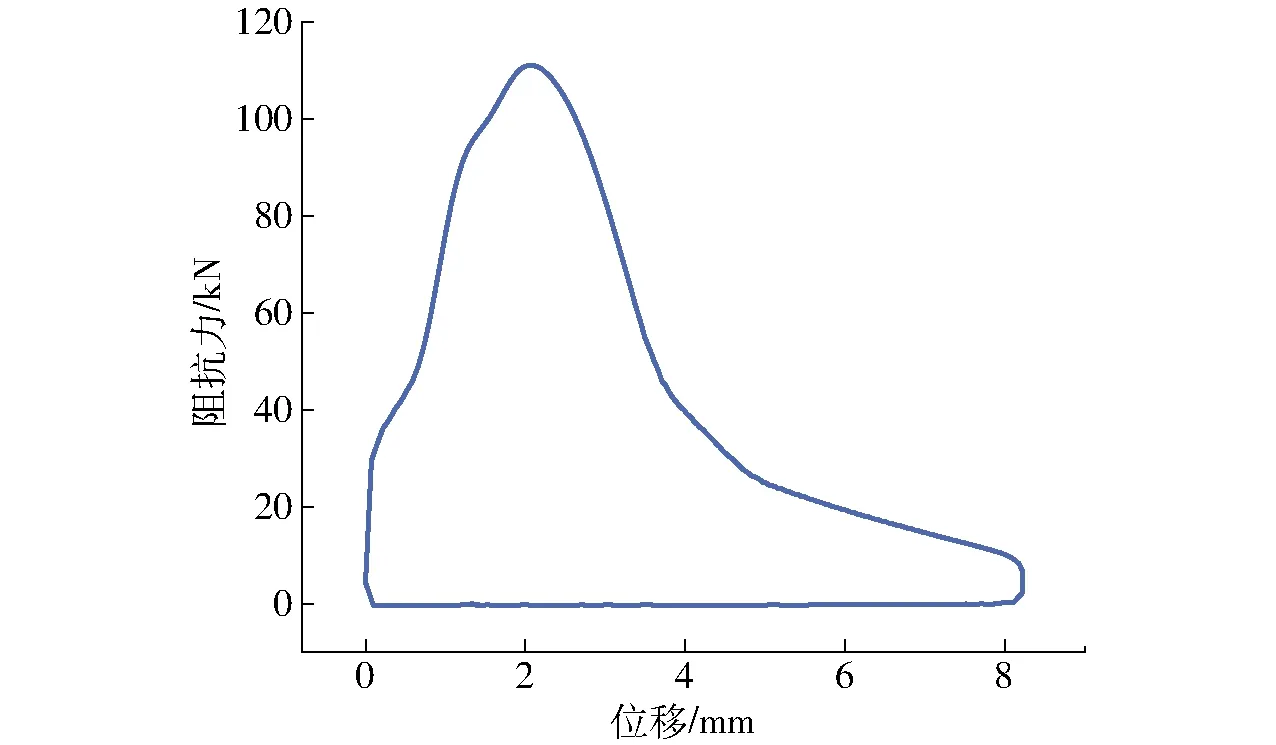
圖15 沖擊運動的滯回曲線Fig.15 Hysteresis loop of impact motion

3 結論

(1)針對某磁流變阻尼器提出了結合磁路有限元分析和計算流體動力學分析的單向耦合仿真研究方法。在實驗驗證勻速準靜態運動模型的基礎上，對模型進行了特定沖擊載荷的流固雙向耦合模擬，獲得了其力學特性規律。

(2)在隱式邊界條件的CFD分析中，解決了粘塑性流體本構定義、非牛頓粘度區的跟蹤和捕獲、以及被動運動的動網格處理等難點。在磁路FE分析得到雙峰分布的磁通密度的基礎上，用雙曲正切函數定義了粘塑性磁流變液的非牛頓粘度，并用“圓函數”準確捕獲非牛頓粘度區。模型也考慮了液體的可壓縮性和多變方程描述的空氣彈簧力。

(3)在沖擊運動過程中，流體域產生大小不一的多個渦，其中最明顯的渦產生于活塞運動方向的后側。磁流變液中的熱量主要產生于環形間隙，最終在活塞一側的平均溫度高于另一側。在持續供電的情況下，阻尼器將無法完全復位，但電路控制可以解決這一問題。