PBL剪力鍵的彈性靜力解析解

司秀勇，劉麗芳，肖 林

(1.燕山大學 建筑工程與力學學院，河北 秦皇島 066004; 2.西南交通大學 土木工程學院, 四川 成都 610031)

由于PBL剪力鍵具有良好的剛度、延性以及疲勞性能，近年來PBL剪力鍵在鋼混組合結構,尤其是橋梁鋼混結合段中的應用越來越廣泛[1-3]。

目前，國內外學者對PBL剪力鍵的承載能力的研究，主要集中于其靜力性能如強度與剛度[4]，研究方法多以試驗尤其是推出試驗為主[5-6]。也有一些學者采用有限元方法進行分析[7-8]，但由于PBL剪力鍵在傳力過程中的高度非線性行為，理論分析的難度較大，相關研究較少。

本文基于Airy應力函數和Winkler彈性地基梁理論，進行鋼混組合結構中PBL剪力鍵在工作狀態下的彈性靜力解析解研究。

1 力學模型的建立

圖1為鋼—混結合段中PBL剪力鍵推出試驗的結構簡圖。

在加載初期，貫穿鋼筋基本不參與工作，主要是由混凝土榫提供抗力；PBL剪力鍵加載中期和加載后期的抗力則主要由貫穿鋼筋提供，此時混凝土榫剪切失效，退化為只傳遞壓力的混凝土圓環[9]。由于鋼板的厚度遠小于混凝土板的厚度。鋼板及鋼板內PBL剪力鍵部分在該方向上的位移受到混凝土巨大剛度的限制，可以將其簡化為一個平面應變問題，如圖2所示；鋼板平面外埋置于混凝土之內的貫穿鋼筋，可以用彈性支撐于混凝土中的Winkler地基梁模擬，如圖3所示。

圖1 PBL剪力鍵的一般構造

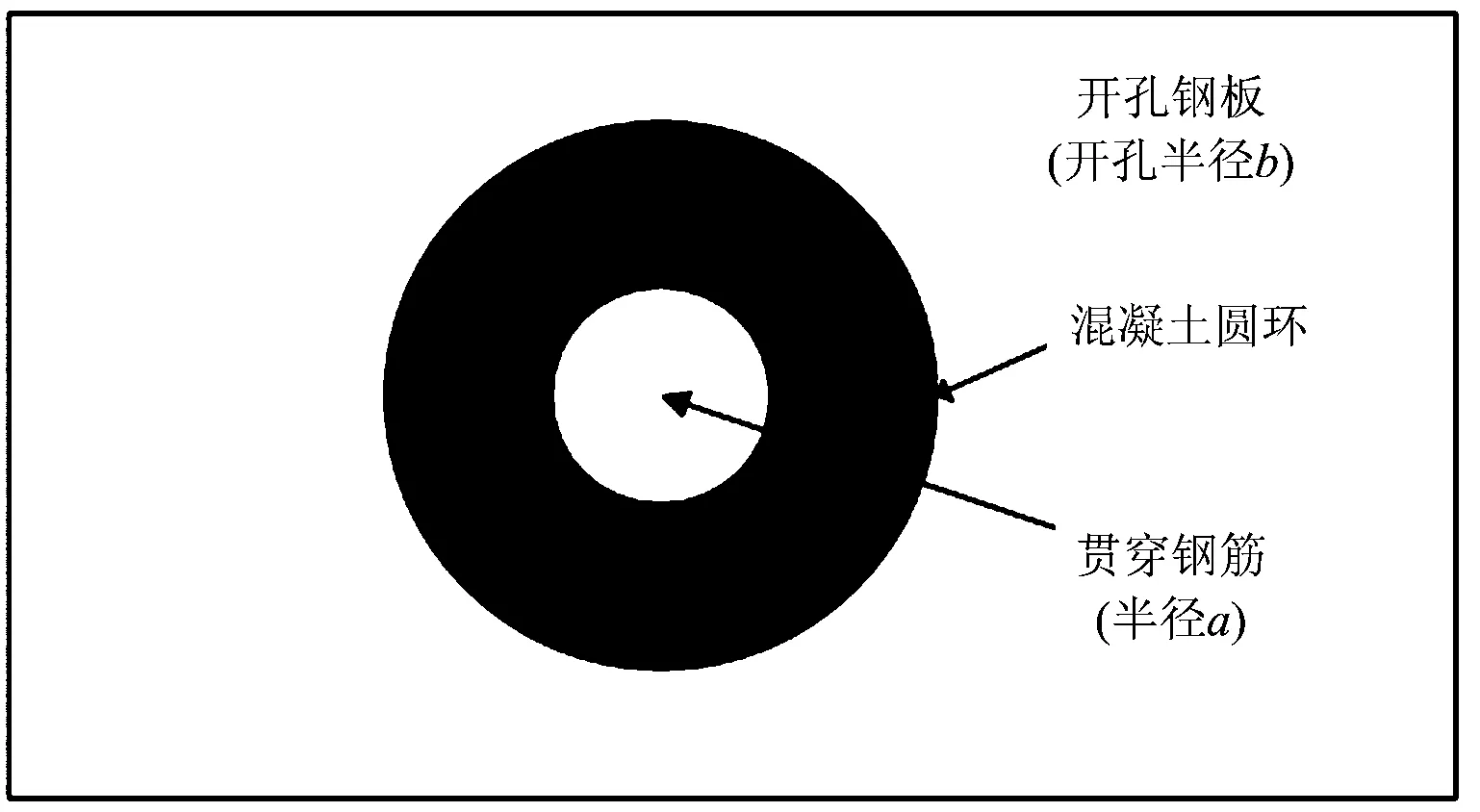
圖2 混凝土圓環平面圖

圖3 貫穿鋼筋的Winkler地基梁模型

2 混凝土圓環力學分析

位于鋼板平面之內PBL剪力鍵，可以將混凝土榫的受力等效為平面應變狀態的厚壁圓環，環的內外壁承受關于x軸的對稱分布荷載。

該問題的解析解可借助于采用極坐標表示的Airy應力函數的一般形式得到。

2.1 基本方程的建立

建立如圖4所示的混凝土圓環的力學模型，坐標原點O取在圓環中心，建立r和θ為坐標的極坐標系。圖中：F1為垂直且指向圓環內表面的分布力的合力，其分布集度設為q1(θ)，分布范圍為[-β1,β1]；F2為垂直且指向圓環外表面的分布力的合力，其分布力集度為q2(θ)，分布范圍為[-β2,β2]。

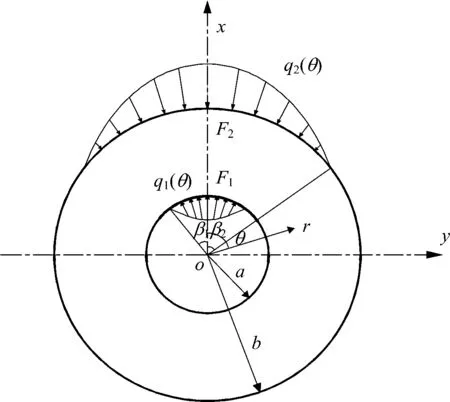
圖4 混凝土圓環的受力狀態簡化模型

根據混凝土圓環受力平衡條件，有

F1=F2

(1)

其中，

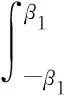
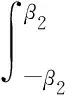
式中：t為鋼板厚度。

借助于Airy應力函數Φ可以得到滿足采用極坐標(r,θ)表示的相容方程為

(2)

應力邊界條件為

(3)

式中：σr和τrθ分別為混凝土圓環沿徑向和環向的應力。

q1(θ)和q2(θ)關于x軸對稱分布，都是偶函數，可以展成傅里葉級數為

(4)

式中：A0，Ai，B0和Bi為待定系數，且有

(5)

假設q1(θ)和q2(θ)為按拋物線形式分布，則可以表示為

(6)

式中：q10和q20為分布載荷的極大值。

由式(6)和式(1)，可以得到q10和q20之間的關系為

(7)

將式(6)代入式(5)中，即可得到傅里葉系數Ai和Bi。

2.2 應力解

在確定傅里葉系數Ai和Bi后，求解式(2)，得到其通解為

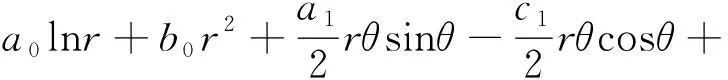
(8)

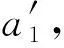
由于整環的位移是單值的，可得

(9)

式中：μ為泊松比。

根據余弦函數的對應系數相等條件以及位移單值條件式(9)，并結合應力邊界條件式(3)和傅里葉級數式(4)等條件，可以求得用傅里葉系數表示的待定系數，分別為

a1=A1a

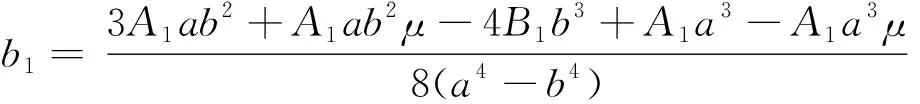
c1=0，d1=0

an=-0.5a2b2(nBna2nb2+n+Ana3n+2-nAnanb2n+2+nAnan+2b2n-Anan+2b2n-nBna2n+2bn-Bna2nbn+2+Bnb3n+2)×[-n2a2nb2n(a2-b2)2+a2b2(a2n-b2n)2]-1(n-1)-1

bn=0.5(nBna2nbn+4+nAnan+4b2n-nBna2n+2bn+2-nAnan+2b2n+2-Anan+2b2n+2-Bna2n+2bn+2+Bna2b3n+2+Ana3n+2b2)[a2b2(a2n-b2n)2-n2a2nb2n(a2-b2)2]-1(n+1)-1

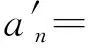
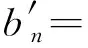
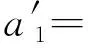
確定待定系數后，代入式(8)可得應力函數。

應力解根據參考文獻[10]，采用彈性力學極坐標中應力分量的經典表達式[10]為

(10)

式中：σθ為混凝土圓環的切向正應力；σz為垂直于混凝土圓環的法向應力。

將已確定待定系數的應力函數代入式(10)即可得到混凝土的應力分量。

2.3 位移解

各個位移和應變分量可以在應力分量確定后，根據彈性力學平面應變問題的物理方程和幾何方程確定。

彈性體的位移可以分為變形位移和剛性位移2部分。所以有

(11)

式中：ur為徑向總位移；uθ為切向總位移；ur1為變形徑向位移；uθ1為變形的切向位移；ur2為剛性徑向位移；uθ2為剛性切向位移。

ur1和uθ1通過積分得到，有

(12)

式中：εr和εθ分別為徑向應變和切向應變。

極坐標下的表達式為

(13)

式中：kx和ky分別為直角坐標系中的平移量；k3為繞z軸的旋轉量。

假設在內表面極坐標(a,π)位置只約束圓環的環向位移，而在(a,0)位置約束圓環的環向位移和徑向位移，則位移邊界條件為

(14)

考慮圓環位移邊界條件、應力邊界條件以及幾何形狀的對稱性，可知uθ2為奇函數，ur2為偶函數，則有ky=0，k3=0。

對式(13)進一步簡化為

(15)

位移最終表達式為

(16)

將式(16)代入式(14)求解出kx。

3 貫穿鋼筋的力學分析

若梁上所受分布載荷集度為q(x)，則由梁的撓曲軸近似微分方程為

(17)

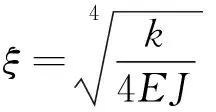
式中：ζ為梁和地基的彈性性質相關的綜合參數；w為任意一點的撓度；EJ為抗彎剛度。

當q(x)不超過x的3次冪時，式(17)的通解為

w=-e-ξx[C1cos(ξx)+C2sin(ξx)]+

(18)

式中：k為基礎彈性系數；C1,C2,C3和C4為待定系數。

以著力點為坐標原點，除原點附近的著力區域外，載荷集度q(x)=0。且由于結構的對稱性，只選取著力點右邊的半段分析。

梁的撓度及內力在離開著力點相當遠處均應趨于0，即C3和C4為0。

著力點處撓曲軸的切線在對稱基礎反力和載荷作用下應為水平，即當x=0時，有

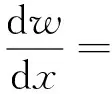
(C1-C2)cos(ξx)]=0

(19)

所以C1=C2。

由此，梁在任一截面x處的撓度ω、轉角φ、彎矩M和剪力Q的計算式為

(20)

當x=0時，式(20)簡化為

(21)

進而可以算出鋼筋的最大彎曲應力σmax和最大剪切應力τmax分別為

(22)

4 算例分析

橋梁中鋼混結合段中PBL剪力鍵的混凝土采用C50，泊松比μ=0.20，彈性模量為EC=34.5 GPa，鋼板厚度為30 mm，開孔半徑b=30 mm，PBL剪力鍵的鋼筋半徑為a=8 mm，彈性模量為Es=206 GPa。假設該PBL剪力鍵在彈性階段的承載力為12.6 kN，混凝土榫與鋼板和鋼筋接觸應力的接觸范圍均為[-π/2,π/2]，亦即β1=β2=π/2，則根據式(1)、式(6)和式(7)計算出q10=32.40 N·mm-1，q20=8.64 N·mm-1。基礎系數k=115 N·mm-3，ζ=0.029 mm-1。

為了驗證本文鋼混組合結構中PBL剪力鍵在工作狀態下的彈性靜力解析解的正確性，在用該文推導的解析解求解的同時采用ANSYS建立有限元模型進行對比分析。

采用ANSYS建立有限元模型時，混凝土圓環采用PLANE42單元，環向網格按每1.5°的角度進行劃分，同一單元徑向網格尺寸與環向網格尺寸近似相等。混凝土圓環的有限元模型如圖5所示。

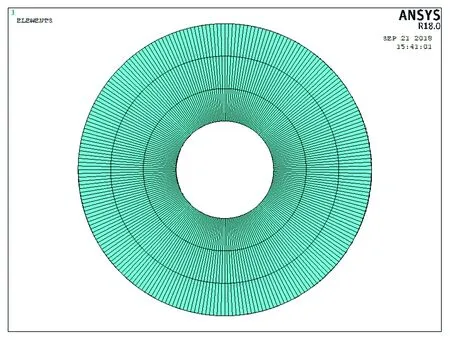
圖5 混凝土圓環的有限元模型

圖6給出了解析解和數值解得到的θ分別為0°，45°，90°，135°和180°時混凝土圓環的徑向位移曲線，徑向位移的方向以沿半徑向外為正。由圖6可以看出：隨著離開圓心距離的增大，混凝土圓環在θ=0°方向上的徑向位移快速增加；混凝土圓環徑向位移在θ大于90°后基本不隨離開圓心距離的變化而變化。各點徑向位移的解析解與數值解吻合程度都較好，其中混凝土圓環在θ=0°，r=30 mm位置徑向位移最大，相對誤差為0.12%。

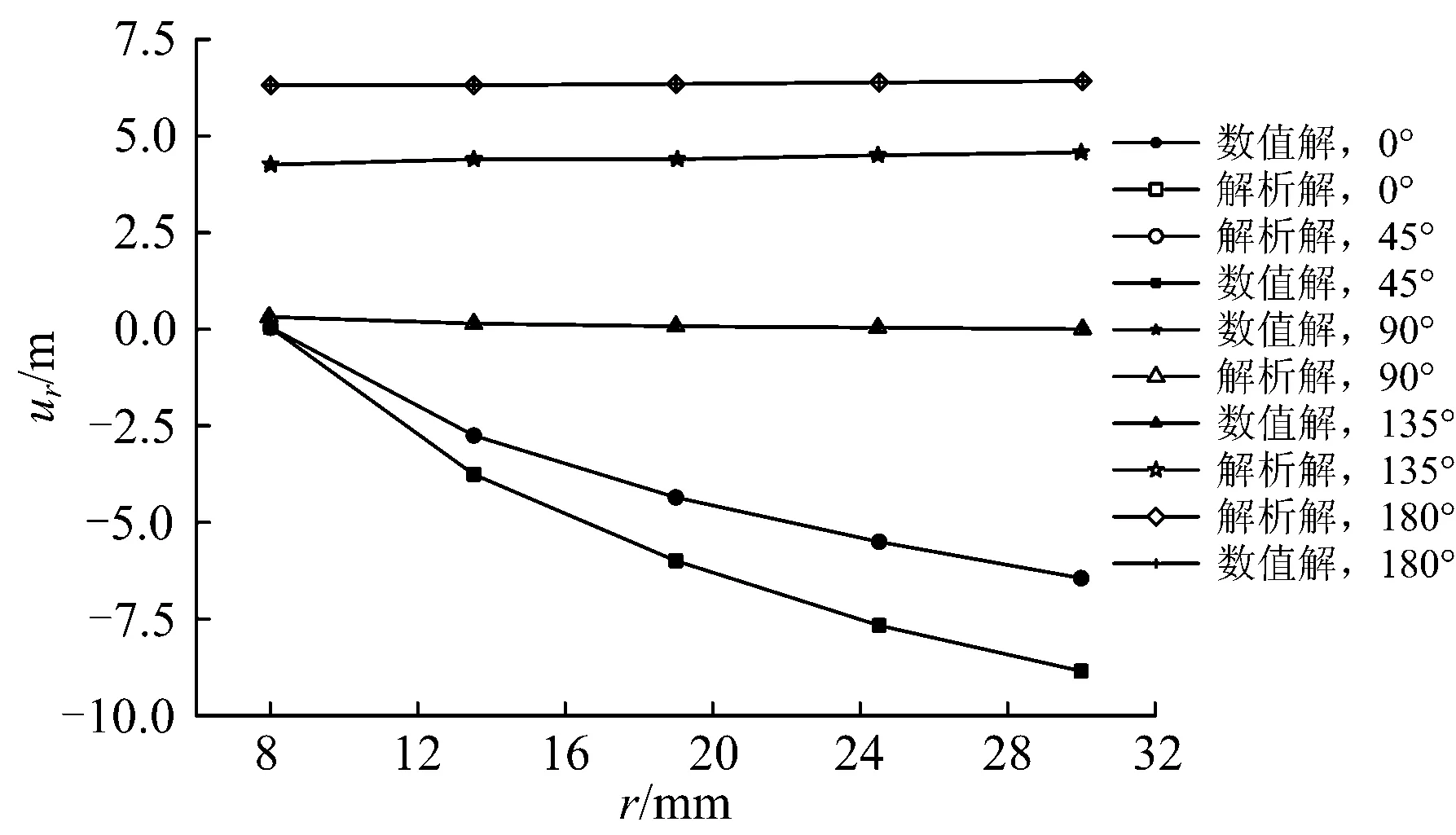
圖6 圓環的徑向位移

θ=0°和θ=180°時，由于結構的對稱性，環向位移為零，混凝土圓環在θ為45°，90°，135°方向上(位移方向以順時針為正)數值解和解析解得到的環向位移曲線如圖7所示。由圖7可以看出，隨著離開圓心距離的逐漸增加，環向位移在θ=45°和θ=90°方向上的變化較在θ=135°方向上變化大。各點環向位移的吻合程度都比較好，其中在θ=90°，r=30 mm位置環向位移最大，相對誤差為1.20%。

θ分別為90°，135°和180°時的徑向應力較小，因此圖8只畫出了θ=0°和θ=45°時解析解和數值解得到的徑向壓應力曲線。由圖8可以看出，隨著離開圓心距離的增加，0°和45°方向上徑向應力逐漸減小，減小速率逐漸減緩。各點徑向應力的吻合程度都較好，其中在θ=0°，r=8 mm位置徑向應力最大，相對誤差為2.50%。

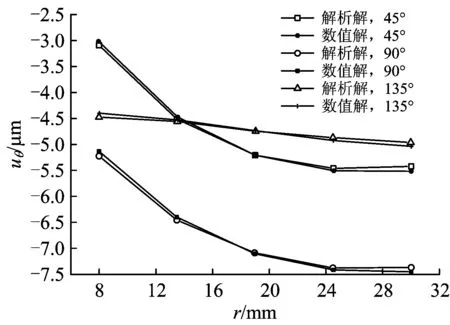
圖7 圓環的環向位移

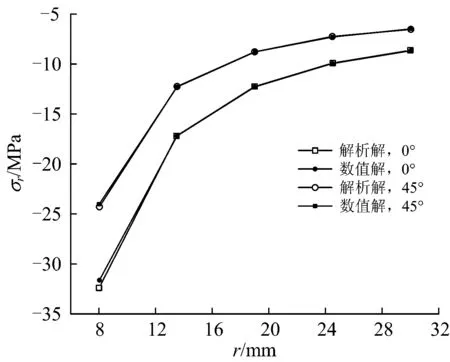
圖8 徑向應力

θ分別為0°，45°，90°，135°和180°時解析解和數值解得到的環向應力(以受拉為正)曲線如圖9所示。由圖9可以看出：0°，45°和90°方向上的環向應力相差較大，而135°和180°方向上的環向應力相差不多。各點環向應力的吻合程度都較好，其中在θ=90°，r=30 mm位置環向應力最大，相對誤差為0.15%。

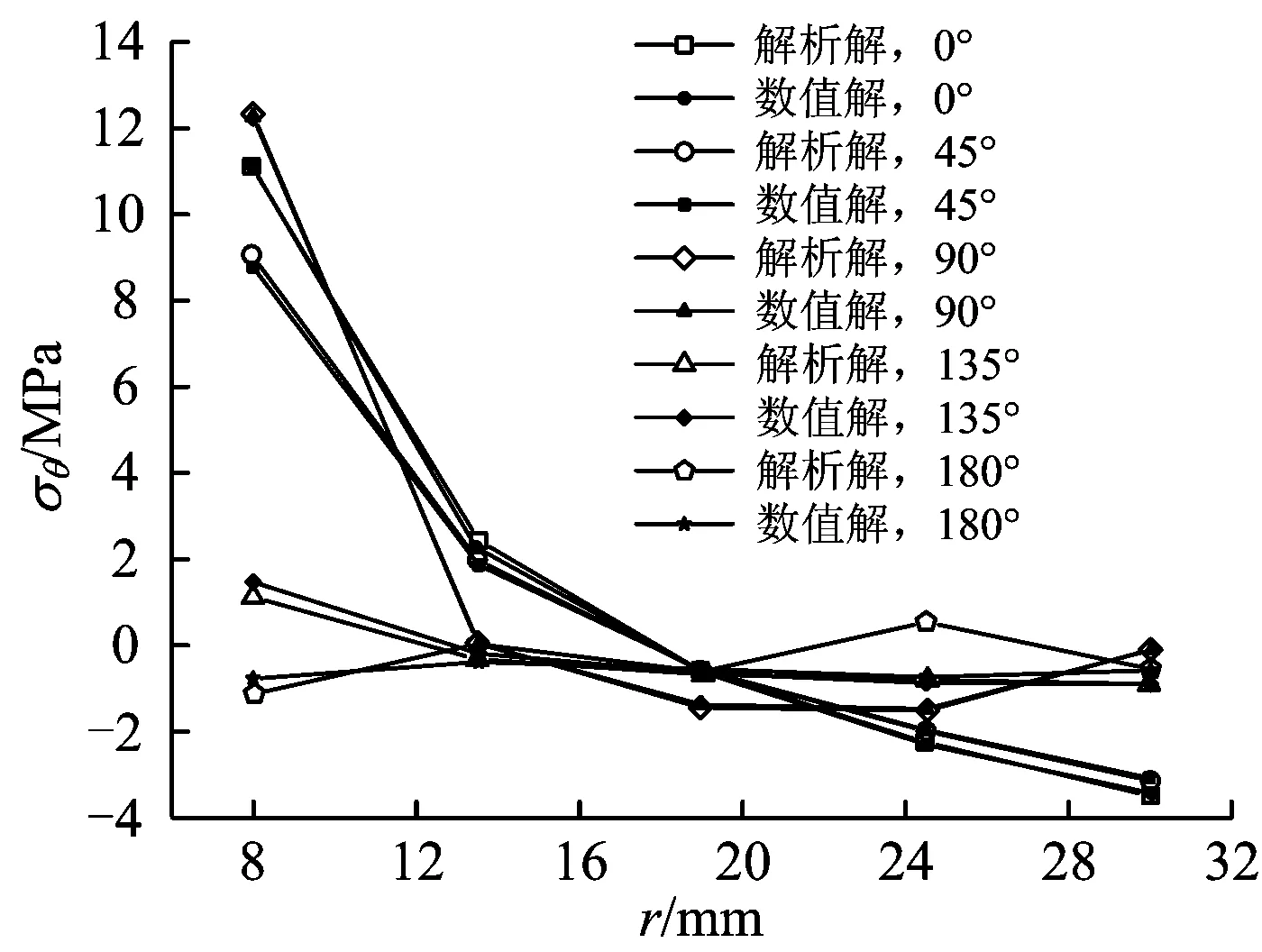
圖9 環向應力

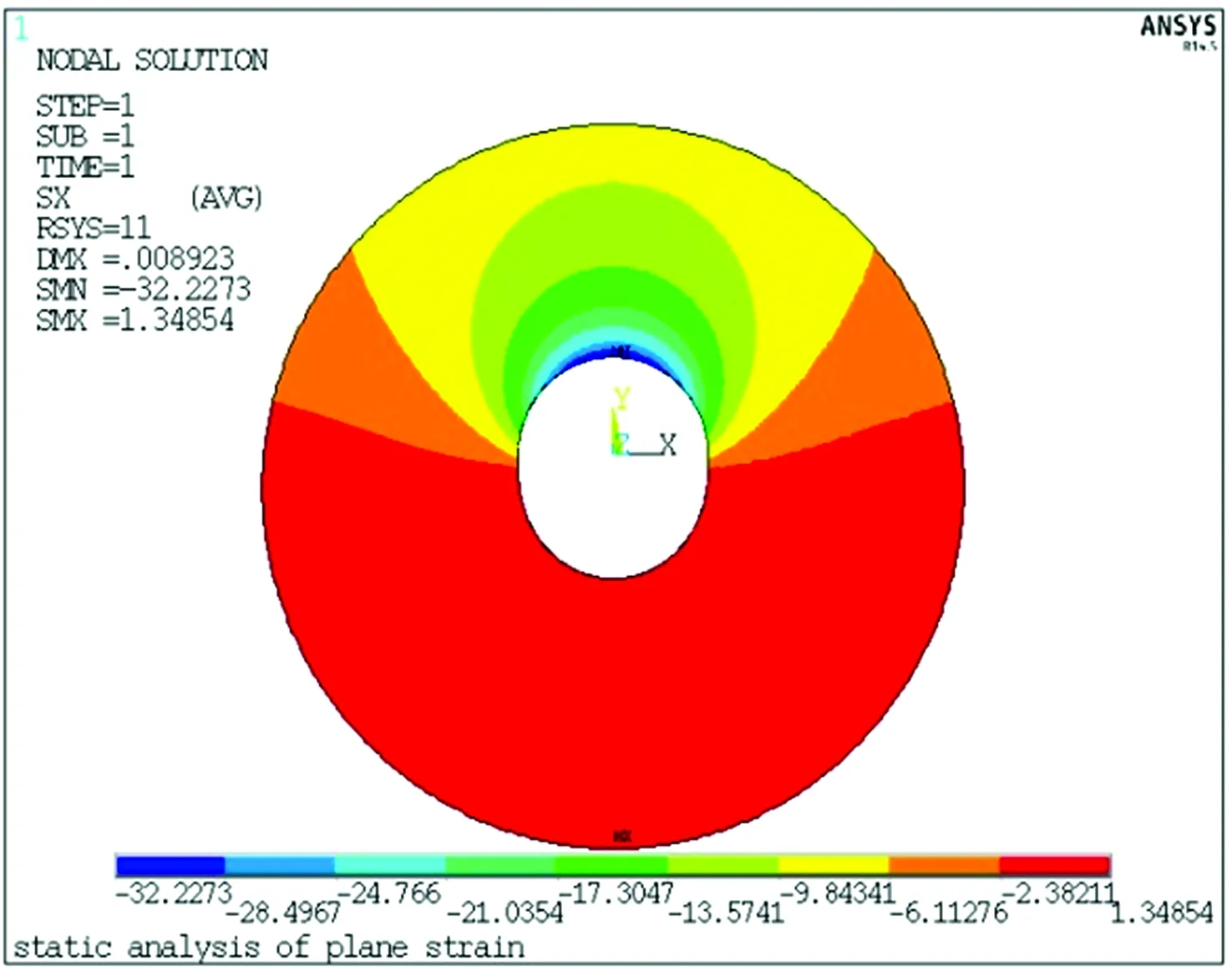
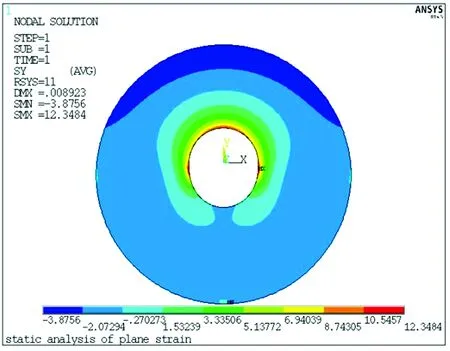
徑向位移云圖、環向位移云圖、徑向應力云圖和環向應力云圖如圖10—圖13所示，各物理量與圖6—圖9具有一致的分布規律。

C50混凝土抗壓強度標準值fck=32.4 MPa，由圖12得知混凝土圓環的最大應力為32.23 MPa，未超過fck，說明混凝土材料處于彈性范圍之內。

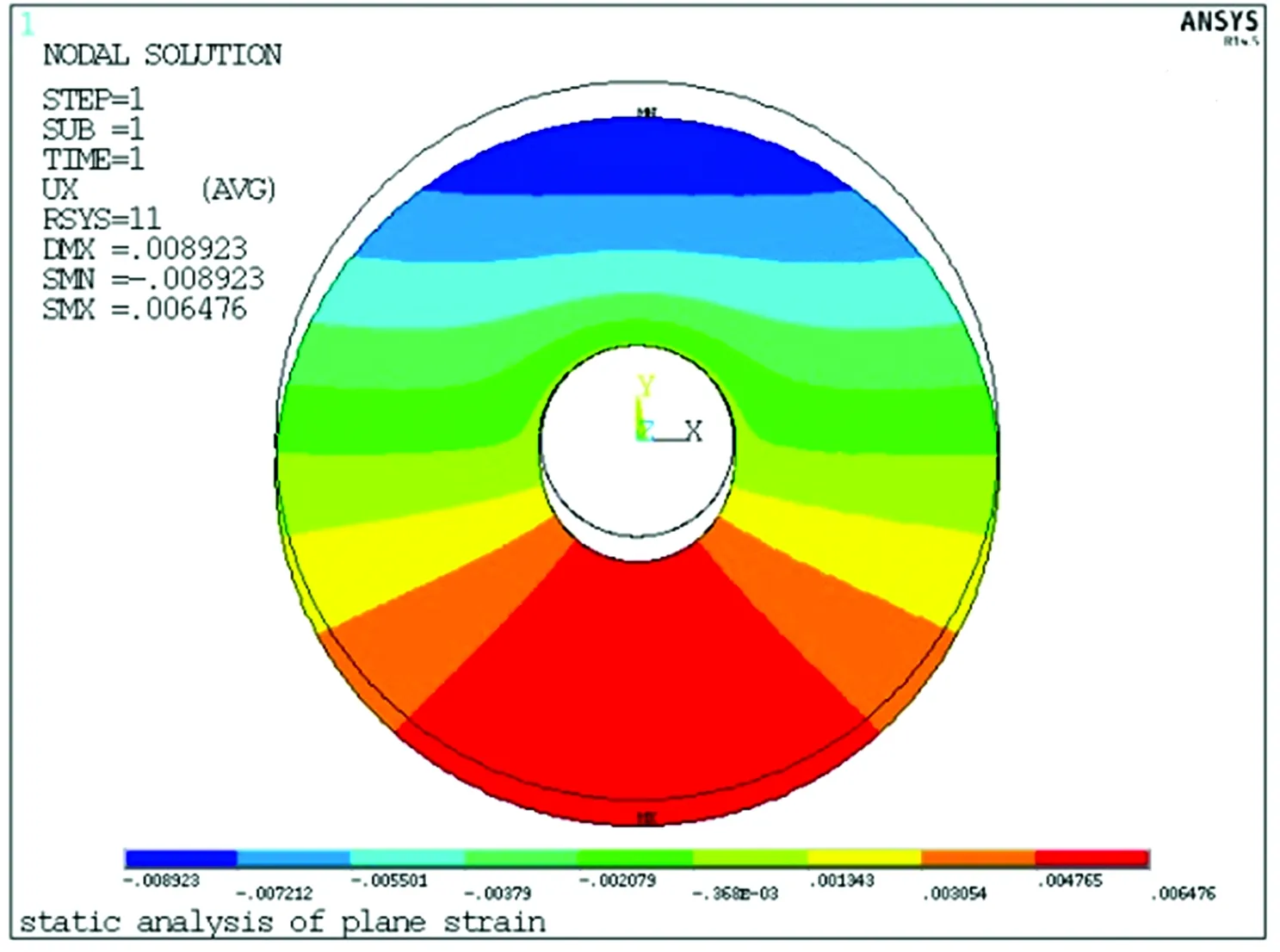
圖10 混凝土圓環徑向位移云圖(單位：mm)

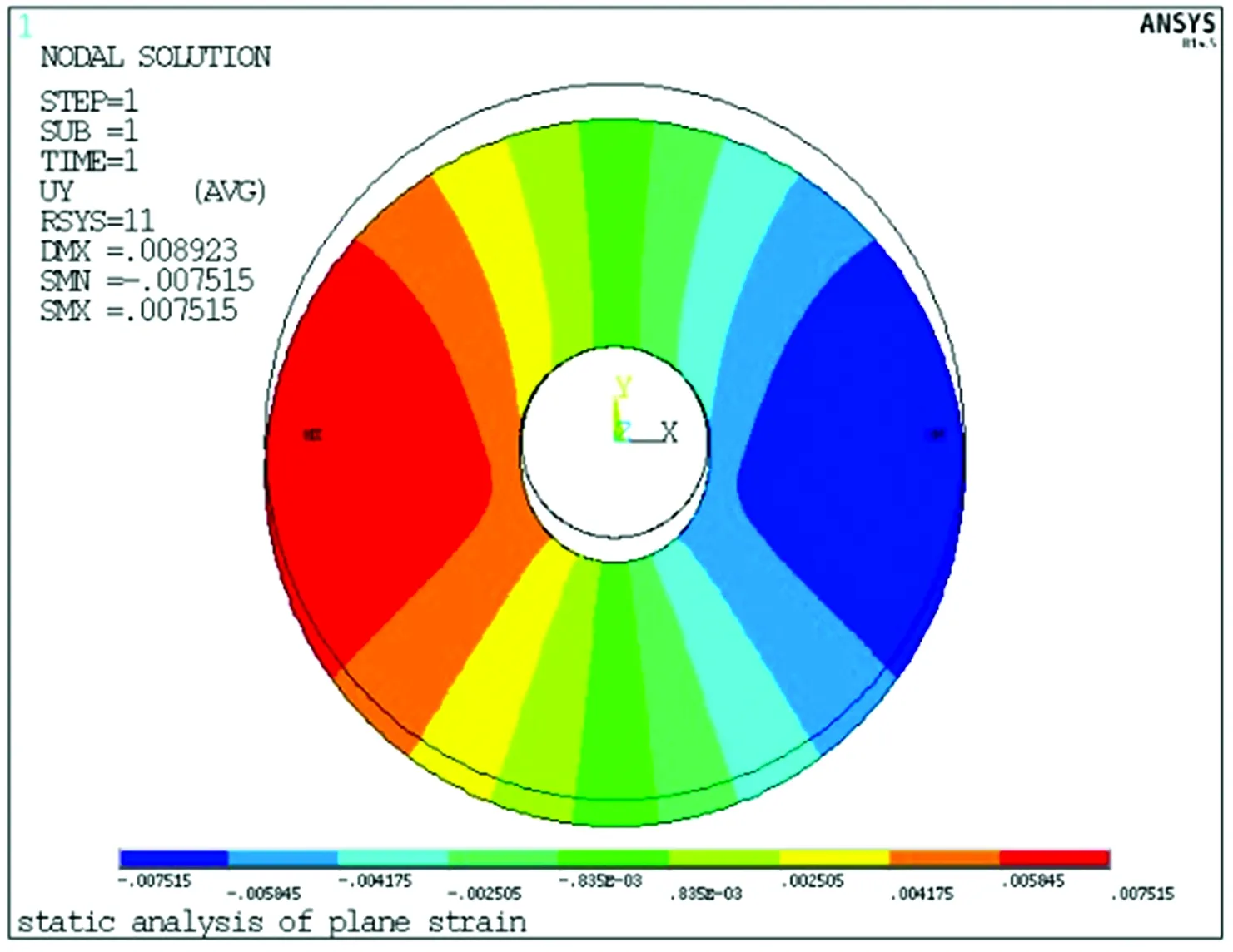
圖11 混凝土圓環環向位移云圖(單位：mm)

對于貫穿鋼筋，根據式(19)和式(20)，可計算得出：w=-0.097 mm，φ=0，M=108.62 N·m，Q=-6.3 kN，σmax=270 MPa

貫穿鋼筋強度滿足要求。

5 結 語

根據現有鋼混凝土組合結構的設計理念，在正常使用階段，PBL剪力鍵大多工作在彈性階段，非線性問題并不突出。因此，根據正常工作狀態下的受力特性，鋼混結合段中單個PBL剪力鍵的彈性受力，可以簡化為貫穿鋼筋的Winkler彈性地基梁和混凝土圓環的平面應變問題。建立簡化力學模型，應用Airy應力函數，求解相應的解析解，通過與有限元分析結果的對比證明了其可靠性。

圖12 混凝土圓環徑向應力云圖(單位：MPa)

圖13 混凝土圓環環向應力云圖(單位：MPa)

本文方法在PBL剪力鍵工作狀態處于線彈性變形階段時有很好的適用性。所得到的混凝土圓環和貫穿鋼筋受力分析的解析解為PBL剪力鍵在工作狀態下的傳力機理的研究、結構優化設計、提高承載能力提供了理論依據和計算方法，同時為PBL剪力鍵在非線性工作狀態下受力分析和求解解析解的研究打下了理論基礎。