基于Capped L1罰函數(shù)的組稀疏模型
崔立鵬,于玲,范平平,吳寶杰,翟永君
(天津輕工職業(yè)技術(shù)學(xué)院電子信息與自動(dòng)化學(xué)院,天津 300350)
1 研究背景
在大數(shù)據(jù)時(shí)代,人們面對(duì)各種各樣的高維數(shù)據(jù),如何從高維數(shù)據(jù)中挖掘出有用的信息是人工智能技術(shù)面臨的一個(gè)重要問題。在現(xiàn)代機(jī)器學(xué)習(xí)、數(shù)據(jù)挖掘與生物信息學(xué)等領(lǐng)域,很多分類和回歸問題的解釋變量空間往往維數(shù)很高,甚至是超高維的。然而,高維數(shù)據(jù)會(huì)導(dǎo)致機(jī)器學(xué)習(xí)中的過擬合現(xiàn)象出現(xiàn),從而使得統(tǒng)計(jì)模型的泛化性能變差。因此,變量空間降維與變量選擇問題亟待解決。變量選擇的目的在于兩個(gè)方面:一是實(shí)現(xiàn)精確的預(yù)測(cè)和分類;二是使得模型具有更好的可解釋性,降低統(tǒng)計(jì)模型的復(fù)雜度。所謂可解釋性指的是模型的簡(jiǎn)潔度,顯然,變量空間維數(shù)越低的統(tǒng)計(jì)模型可解釋性越好。總之,人們總是期望盡可能利用較少的變量實(shí)現(xiàn)更高的預(yù)測(cè)準(zhǔn)確性。如何實(shí)現(xiàn)統(tǒng)計(jì)模型的變量空間降維?很多統(tǒng)計(jì)學(xué)家針對(duì)變量空間降維的問題展開了研究,從而提出了一系列的稀疏模型,最著名的當(dāng)屬Tibishirani提出的Lasso[1]。考慮線性回歸模型b,其中X∈RN×P為全部解釋變量(自變量)的觀測(cè)值所構(gòu)成的矩陣,β∈RP稱作模型向量或回歸系數(shù)向量,y∈RN稱作響應(yīng)向量、因變量向量或輸出向量,ε∈RN為噪聲向量且λ1>0為樣本數(shù),a>1為變量數(shù)。由Tibshirani提出的著名的 Lasso 的形式為λ?‖β‖1,其中 λ>0 為調(diào)節(jié)參數(shù)(Tuning Parameter),‖β‖1為L(zhǎng)1范數(shù)罰。L1范數(shù)罰由于在零點(diǎn)處不可導(dǎo)從而可產(chǎn)生稀疏解,利用子梯度(Subgradient)可得單變量時(shí)其解的形式,其中為最小二乘解。顯然,此時(shí)其解為軟閾值算子(Soft-Threshold Operator)形式,從而將絕對(duì)值小于λ的回歸系數(shù)置零,實(shí)現(xiàn)變量選擇與統(tǒng)計(jì)模型的稀疏化。
Lasso在統(tǒng)計(jì)學(xué)中的變量選擇領(lǐng)域具有極其重要的地位。然而,學(xué)者們通過實(shí)驗(yàn)與理論分析發(fā)現(xiàn),Lasso也存在各種各樣的缺點(diǎn),很多學(xué)者針對(duì)Lasso的這些缺點(diǎn)進(jìn)行了更深入的研究,其中之一就是Lasso對(duì)重要變量的系數(shù)也進(jìn)行壓縮,Zhao等人指出其只在非常強(qiáng)的附加條件下才具有Oracle性質(zhì)[2],SCAD模型[3]、MC模型[4]和自適應(yīng)Lasso[5,6]等統(tǒng)計(jì)模型克服了Lasso的這一缺點(diǎn),與Lasso相比,它們顯著減小了對(duì)重要變量的回歸系數(shù)的壓縮程度,因而這些模型具有所謂的Oracle性質(zhì)。另外,Lasso在面對(duì)一組彼此之間存在高度相關(guān)性的解釋變量時(shí),往往只能選擇出其中的一小部分,克服了這一缺點(diǎn)的稀疏模型為Elastic Net[7],其往往能夠?qū)⒁唤M彼此間存在高度相關(guān)性的變量中的大部分選擇出來。Lasso只能實(shí)現(xiàn)分散的變量選擇,很多情形下變量之間存在某種結(jié)構(gòu),例如在基因微陣列分析中,某基因上往往會(huì)有多個(gè)變異點(diǎn),在識(shí)別究竟是哪個(gè)基因發(fā)生的變異與所發(fā)生疾病存在關(guān)聯(lián)關(guān)系時(shí)將屬于同一個(gè)基因的變異點(diǎn)分為一個(gè)組是更加合理的,因此有學(xué)者考慮將變量之間存在的結(jié)構(gòu)作為先驗(yàn)信息再進(jìn)行變量選擇,Group Lasso[8-10]就是將變量的組結(jié)構(gòu)作為先驗(yàn)信息的稀疏模型,其具有變量組選擇功能。除了應(yīng)用于統(tǒng)計(jì)學(xué)上的變量選擇問題,Lasso等稀疏模型還被應(yīng)用到了壓縮感知、信號(hào)重構(gòu)和圖像重構(gòu)等諸多領(lǐng)域,在生物統(tǒng)計(jì)、機(jī)器學(xué)習(xí)、數(shù)據(jù)挖掘、圖像處理和信號(hào)處理等領(lǐng)域有著越來越廣泛的應(yīng)用。
基于上述思想,將Capped L1罰[11]推廣到變量組選擇的情況下,提出了一種新的組稀疏模型:Group Capped L1模型,其具有變量組選擇能力。最后,通過人工數(shù)據(jù)集實(shí)驗(yàn)驗(yàn)證了其在變量選擇和預(yù)測(cè)等方面的有效性。
2 Group Capped L1模型
2.1 Capppeedd .1罰
Capped L1罰的形式為:
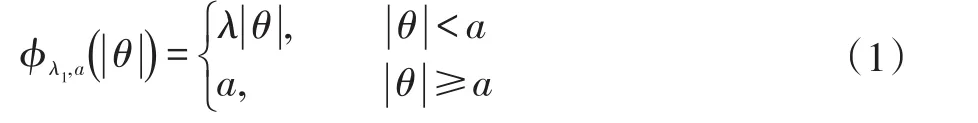
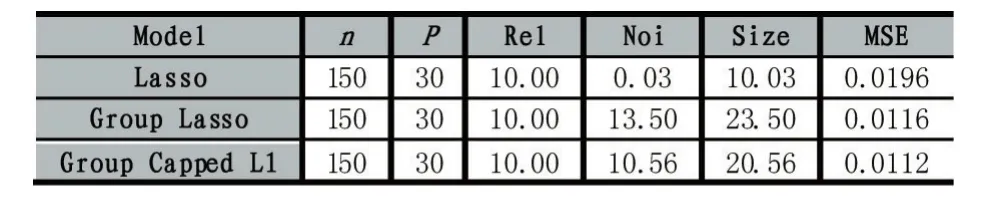
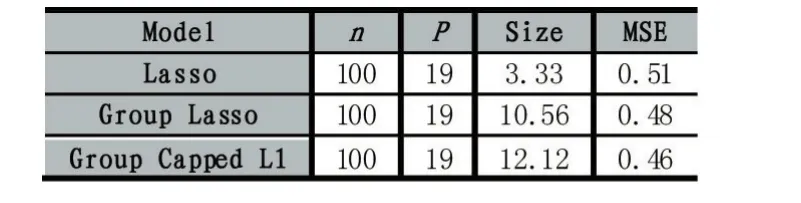
其中λ和a均為可調(diào)參數(shù),λ>0且a>0。顯然,Capped L1罰由兩部分構(gòu)成,||θ 圖1 Capped L1罰的圖像 Capped L1模型在回歸系數(shù)小于等于a時(shí)表現(xiàn)出與Lasso一致的變量選擇特性,而在回歸系數(shù)大于a時(shí)不對(duì)回歸系數(shù)進(jìn)行壓縮,其克服了Lasso對(duì)所有回歸系數(shù)均進(jìn)行壓縮的缺點(diǎn),但其仍然只能實(shí)現(xiàn)變量水平上的稀疏性,不能實(shí)現(xiàn)變量組水平上的稀疏性。下面將Capped L1罰推廣到變量組選擇情形,構(gòu)成具有組稀疏性的Group Capped L1模型。 已知如下的線性回歸模型: 其中 β為P×1維的系數(shù)向量,X為n×P階的設(shè)計(jì)矩陣,y為n×1維的輸出向量,且噪聲服從高斯分布: 事先將P個(gè)變量劃分為J個(gè)組,利用 βj代表第 j個(gè)變量組對(duì)應(yīng)的系數(shù)向量,Xj代表第 j個(gè)變量組對(duì)應(yīng)的子設(shè)計(jì)矩陣,dj表示第 j個(gè)變量組中的變量數(shù),不妨假設(shè)任意的子設(shè)計(jì)矩陣Xj均滿足正交條件XjTXj=Idj,其中dj階的單位方陣,j∈{1 ,2,…,J} ,不妨假設(shè)xijp表示對(duì)第 j個(gè)變量組中的第p個(gè)變量的觀測(cè)值,則Group Capped L1模型為: 其中 φλ1,a(?)為Capped L1罰,λ1和a均為可調(diào)參數(shù)。 下面利用塊坐標(biāo)下降算法求解Group Capped L1模型。塊坐標(biāo)下降算法在求解稀疏模型時(shí)需要該模型關(guān)于單變量組的顯式解,然后不斷迭代直到滿足收斂條件。塊坐標(biāo)下降算法是坐標(biāo)下降算法的推廣,坐標(biāo)下降算法最初用來求解Lasso問題,其思想為在求解優(yōu)化問題時(shí)每次迭代中只關(guān)于一個(gè)變量進(jìn)行優(yōu)化,同時(shí)固定其余所有變量的值不變,這樣就將復(fù)雜的多維優(yōu)化問題轉(zhuǎn)化為一系列的單維優(yōu)化問題,大大降低了計(jì)算的復(fù)雜度。塊坐標(biāo)下降算法在求解優(yōu)化問題時(shí)每次迭代中只關(guān)于一個(gè)變量組進(jìn)行優(yōu)化,同時(shí)固定其余所有變量組的值不變,經(jīng)過若干次迭代得到模型的解。由于Capped L1罰是一個(gè)分段函數(shù),因此討論Group Capped L1模型關(guān)于單變量組的顯式解時(shí)需要分情況進(jìn)行討論。Group Capped L1模型關(guān)于第 j個(gè)變量組的解可被表示為: 在Group Capped L1模型關(guān)于單變量組的顯式解的基礎(chǔ)上,可利用塊坐標(biāo)下降算法求解Group Capped L1模型。求解Group Capped L1模型的塊坐標(biāo)下降算法為: (1)輸入響應(yīng)向量y、設(shè)計(jì)矩陣X、回歸系數(shù)向量的初始值β。 (2)當(dāng)1≤j≤J時(shí)重復(fù)執(zhí)行下列步驟: ②利用公式(5)求解 βj。 ③更新 β中的第 j個(gè)子系數(shù)向量 βj。 ④令 j=j+1。 (3)得到遍歷一次全部分組后的回歸系數(shù)向量β,判斷是否滿足預(yù)先設(shè)定的收斂條件或迭代次數(shù),若不滿足則跳轉(zhuǎn)到第(2)步;否則,結(jié)束算法。 (4)輸出回歸系數(shù)向量β。 下面利用人工生成的數(shù)據(jù)集進(jìn)行實(shí)驗(yàn)驗(yàn)證Lasso、Group Lasso、Group Capped L1等稀疏模型在線性回歸模型下的變量選擇能力。在生成的全部人工數(shù)據(jù)集的實(shí)驗(yàn)中,對(duì)每個(gè)數(shù)據(jù)集中的變量都隨機(jī)劃分成兩個(gè)樣本數(shù)相同的子數(shù)據(jù)集,其中一份作為訓(xùn)練數(shù)據(jù)集,另一份作為測(cè)試數(shù)據(jù)集,上述劃分過程重復(fù)30次,得到30個(gè)實(shí)驗(yàn)結(jié)果,取30次實(shí)驗(yàn)結(jié)果的均值作為最終的實(shí)驗(yàn)結(jié)果,將實(shí)驗(yàn)結(jié)果列入各個(gè)表中,表中n表示訓(xùn)練樣本數(shù),P表示變量總數(shù),Size表示選出的變量總數(shù),Rel表示識(shí)別出的目標(biāo)變量數(shù),Noi表示剔除的冗余變量數(shù),MSE 表示預(yù)測(cè)均方誤差(Mean Square Error),Error表示錯(cuò)誤分類率。 生成如下兩種不同類型的數(shù)據(jù)集:人工數(shù)據(jù)集1和人工數(shù)據(jù)集2,其中人工數(shù)據(jù)集1中每個(gè)變量組所含的變量數(shù)相等,而人工數(shù)據(jù)集2中各變量組所含的變量數(shù)不相等。人工數(shù)據(jù)集1和人工數(shù)據(jù)集2均基于線性回歸模型y=Xβ+ε生成。 人工數(shù)據(jù)集1:該數(shù)據(jù)集包含2n=300個(gè)樣本和P=30個(gè)變量,這30個(gè)變量被劃分為6個(gè)變量組。人工數(shù)據(jù)集2:該數(shù)據(jù)集包含2n=200個(gè)樣本和P=20個(gè)變量,這20個(gè)變量被劃分為4個(gè)變量組。實(shí)驗(yàn)結(jié)果如表1和表2所示,從實(shí)驗(yàn)結(jié)果可以看出,對(duì)于人工數(shù)據(jù)集1來說,Group Capped L1模型具有明顯的稀疏性,能夠?qū)崿F(xiàn)變量組選擇,并且其預(yù)測(cè)均方誤差最小。 表1 人工數(shù)據(jù)集1的實(shí)驗(yàn)結(jié)果 表2 人工數(shù)據(jù)集2的實(shí)驗(yàn)結(jié)果 選取來自Hosmer與Lemeshow收集的新生兒體重?cái)?shù)據(jù)集(Birthweight Dataset)來對(duì) Lasso、Group Lasso以及Group Capped L1這幾種組稀疏模型進(jìn)行實(shí)驗(yàn)。該數(shù)據(jù)集包含189個(gè)新生兒的體重以及可能與新生兒體重有關(guān)的8個(gè)解釋變量,該8個(gè)變量分別為:母體年齡、母體體重、種族(白人或黑人)、吸煙史(吸煙或不吸煙)、早產(chǎn)史(早產(chǎn)過一次或早產(chǎn)過兩次)、高血壓史(有高血壓史或無高血壓史)、子宮刺激性史(有子宮刺激性史或無子宮刺激性史)、懷孕期間的物理檢查次數(shù)(一次、兩次或三次),其中母體年齡和母體體重為用三次多項(xiàng)式表示的連續(xù)變量,而其余六個(gè)解釋變量均為分類變量。對(duì)于母體年齡和母體體重,其可被視為用屬于同一個(gè)組的三個(gè)變量來表示。對(duì)于分類變量,其所對(duì)應(yīng)的多個(gè)水平可被視為多個(gè)變量,這些變量屬于分類變量這個(gè)組。因此,該數(shù)據(jù)集可被視為含有19個(gè)變量和189個(gè)樣本,并且這19個(gè)變量被分為8個(gè)變量組。另外,該數(shù)據(jù)集還包含兩個(gè)輸出變量bwt和low,其中輸出變量bwt為連續(xù)變量,表示新生兒的體重值;變量low為二值變量,表示新生兒的體重值是大于2.5kg還是小于2.5kg。當(dāng)以變量bwt為輸出變量時(shí),為線性回歸模型問題;當(dāng)以變量low為輸出變量時(shí),為二分類問題。 將189個(gè)變量隨機(jī)劃分成兩個(gè)分別含有100個(gè)樣本和89個(gè)樣本的子數(shù)據(jù)集,其中含有100個(gè)樣本的子數(shù)據(jù)集作為訓(xùn)練數(shù)據(jù)集,另一份含有89個(gè)樣本的子數(shù)據(jù)集作為測(cè)試數(shù)據(jù)集,上述劃分過程重復(fù)100次,得到100個(gè)實(shí)驗(yàn)結(jié)果,取100次實(shí)驗(yàn)結(jié)果的均值作為最終的實(shí)驗(yàn)結(jié)果。實(shí)驗(yàn)結(jié)果如表3所示,表3是以bwt為輸出變量的實(shí)驗(yàn)結(jié)果,表中n表示訓(xùn)練樣本數(shù),P表示變量總數(shù),Size表示選出的變量總數(shù),MSE表示預(yù)測(cè)均方誤差。從表3中的實(shí)驗(yàn)結(jié)果可以看出,在回歸問題下,Group Capped L1的預(yù)測(cè)均方誤差最小,而且其得到的模型稀疏性也較好,與Lasso和Group Lasso相比,是一種更好的變量選擇模型。 表3 新生兒體重?cái)?shù)據(jù)集的實(shí)驗(yàn)結(jié)果 在機(jī)器學(xué)習(xí)和生物信息學(xué)中,有時(shí)變量之間存在一定的組結(jié)構(gòu),忽略這種組結(jié)構(gòu)是不恰當(dāng)?shù)摹1疚膶⒔M結(jié)構(gòu)作為先驗(yàn)信息,把Capped L1罰推廣到變量組選擇的情形下,基于Capped L1罰提出了一種新的組稀疏模型,其能夠?qū)崿F(xiàn)變量組選擇,通過人工數(shù)據(jù)集實(shí)驗(yàn)和真實(shí)數(shù)據(jù)集實(shí)比較了其與Lasso、Group Lasso在變量選擇方面、預(yù)測(cè)準(zhǔn)確性和分類錯(cuò)誤率等方面的性能,實(shí)驗(yàn)結(jié)果說明了提出的基于Capped L1罰的組稀疏模型在變量選擇方面和預(yù)測(cè)方面的有效性。本文只是在線性回歸模型下研究了其變量選擇等性能,后續(xù)將其推廣到邏輯斯蒂回歸模型下的情況值得進(jìn)一步探索。當(dāng)前,稀疏模型仍然是機(jī)器學(xué)習(xí)領(lǐng)域的研究熱點(diǎn),其有意義的研究方向有如下幾個(gè)方面:第一,將稀疏模型向除線性回歸模型以外的其它統(tǒng)計(jì)模型進(jìn)行拓展。當(dāng)前,由于線性回歸模型的簡(jiǎn)潔性,大多稀疏模型均基于線性回歸模型提出,但線性回歸模型的應(yīng)用場(chǎng)景有限,將這些稀疏模型向COX比例風(fēng)險(xiǎn)回歸模型、Tobit模型和Probit模型等其它統(tǒng)計(jì)模型推廣是必要的,現(xiàn)在該方向仍然有大量工作需要進(jìn)一步完成。第二,對(duì)稀疏模型統(tǒng)計(jì)性質(zhì)的理論分析。很多稀疏模型通過實(shí)驗(yàn)驗(yàn)證了其變量選擇的準(zhǔn)確性,但尚缺乏變量選擇一致性和參數(shù)估計(jì)一致性等理論分析方面的支撐,例如PEN SVM的變量選擇一致性和參數(shù)估計(jì)一致性尚未被研究。另外,已有學(xué)者給出了Group Lasso等稀疏模型實(shí)現(xiàn)一致性等統(tǒng)計(jì)性質(zhì)需要的假設(shè)條件,但這些已知條件較為復(fù)雜,如何對(duì)其進(jìn)行簡(jiǎn)化值得探究。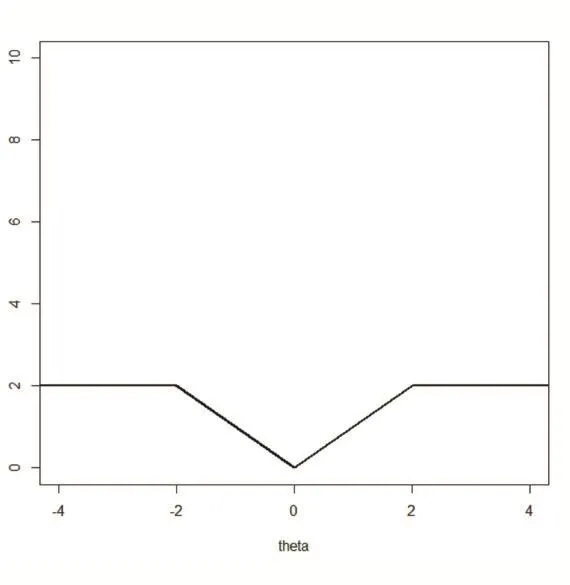
2.2 Group Cappeed L 1模型的形式


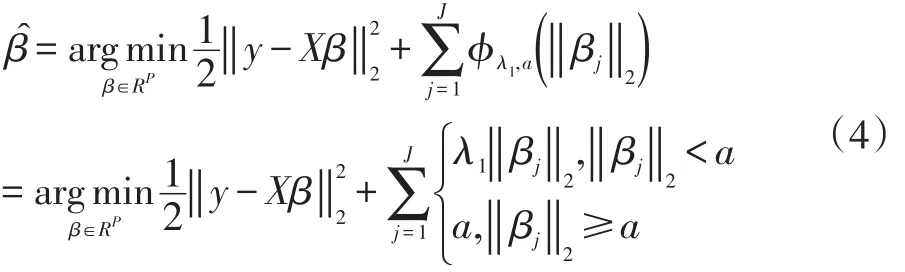
2.3 Group Cappeed L 1模型的求解算法
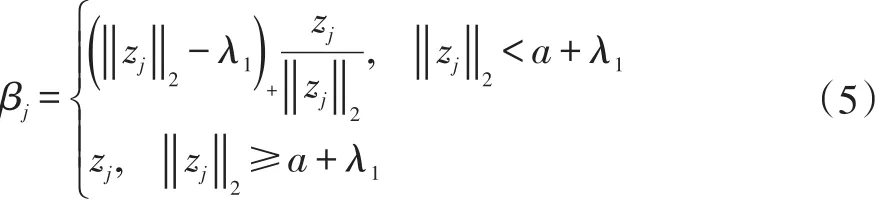
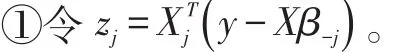
3 實(shí)驗(yàn)
3.1 人工數(shù)據(jù)集實(shí)驗(yàn)

3.2 真實(shí)數(shù)據(jù)集實(shí)驗(yàn)
4 結(jié)語
- 現(xiàn)代計(jì)算機(jī)的其它文章
- 大數(shù)據(jù)時(shí)代下探索大學(xué)生創(chuàng)新創(chuàng)業(yè)能力的培養(yǎng)
- 專業(yè)認(rèn)證標(biāo)準(zhǔn)下改進(jìn)MATLAB課程教學(xué)的研究與實(shí)踐
- 基于協(xié)同過濾的個(gè)性化民宿推薦系統(tǒng)的設(shè)計(jì)與實(shí)現(xiàn)
- 軍人體能考核成績(jī)計(jì)算系統(tǒng)設(shè)計(jì)與實(shí)現(xiàn)
- 基于Blockly的兒童編程思維訓(xùn)練App設(shè)計(jì)
- 基于MC20模塊的GPS/北斗定位系統(tǒng)的實(shí)驗(yàn)設(shè)計(jì)

