約瑟夫問題分析
劉薇,陳文
(福州職業技術學院,福州 350108)
1 約瑟夫問題
約瑟夫問題是計算機算法中的經典問題,對約瑟夫問題的研究由來已久[1],對約瑟夫問題的算法分析對于計算機程序設計的教學具有重要的作用[2]。約瑟夫問題的描述方式有多種形式[3],但其本質是一樣的。以下對約瑟夫問題給出一種描述方式:編號為1到n的n個人,按編號順序圍成一圈,即初始狀態時,第n個的下一個為第1個。從1開始往后報數,報到k的倍數的人離開。如此繼續,直到只剩最后一人為止。問最后留下的是n個人中的哪一個。
對于約瑟夫問題,最直觀和最常用的方法便是順序存儲的數組標記法和利用循環鏈表的結點刪除法。本文著重介紹除此之外的約瑟夫問題的其他解法,包括順推法、逆推法、遞歸法等,進一步拓展解決問題的思路。并對各種方法進行分析對比,提高程序設計能力。
2 約瑟夫問題的解決方法
2.1 數組標記法
數組標記法是較為直觀的一種算法[4]。它的基本思想就是直接用數組data[1],data[2],…,data[n]標記n個人的狀態,值為1時,表示該元素已出局。初始狀態data[1],data[2],…,data[n]的值均為0。當前編號current=0。從當前位置往后找非1元素。找k次后,將當前位置的數組值置為1。如此重n-1次,則,數組中值為0的下標編號即為所求。算法如下:
(1)從當前位置 current處尋找下一個值為 0位置。
int nextZero(int data[],int n,int current){
current=current%n+1;//后移一位
while(data[current]!=0)
current=current%n+1;
return current;
}
(2)求解約瑟夫問題的主程序為:int main(){
定義變量,輸入n,k;
初始數組data[1]---data[n];
current=0;
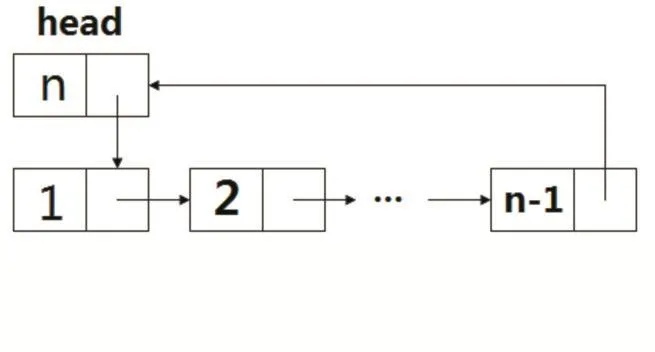
for(kill=1;kill { for(i=1;i<=k;i++) //報 k 次 current=nextZero(data,n,current); data[current]=1;//當前位置出局 } for(i=1;i<=n;i++){ if(data[i]==0){輸出i;break;} //查找數據值為0的數組下標 } } 利用循環鏈表的方法解決約瑟夫問題,也是較為常用的方法之一。有學者對此算法的優劣做了較為詳細的分析[5],也有學者利用不同的程序設計語言進行相應的描述。本文利用《C語言程序設計》給出算法的描述。它的基本思想是:建立如下循環鏈表。 圖1 循環鏈表示意圖 當前位置current初始狀態時為head,則算法描述為:當前位置current往后移k-1次后,將current的下一個元素刪除。如此重復n-1次,則current的值即為所求。 (1)結點結構:struct node { int data; struct node*next; //下一結點的地址 }; typedef struct node Llist; (2)鏈表創建 Llist*creat(int n){ Llist*head,*rear,*t; head=(Llist*)malloc(sizeof(node)); head->data=n; rear=head; int i; for(i=1;i<=n-1;i++){ t=(Llist*)malloc(sizeof(node)); t->data=i; rear->next=t; rear=t; } rear->next=head; return head; } 求解約瑟夫問題的主程序為:int main(){ 定義參數,輸入n,k Llist*h,*t; h=creat(n);//創建初始鏈 for(kill=1;kill for(i=1;i h=h->next; t=h->next;//t為第k個元素位置h->next=t->next; free(t);//將第 k 個元素刪除} printf("i=%d
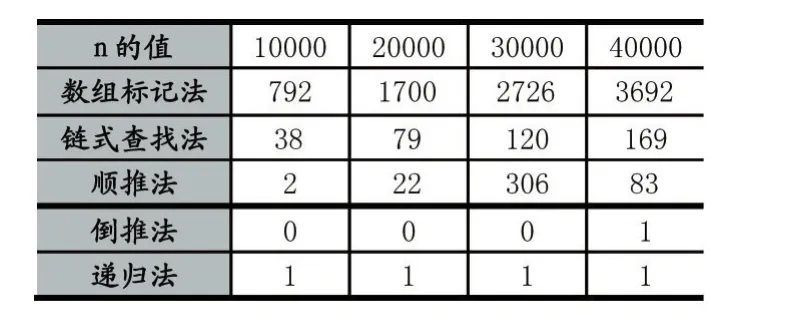
",h->data); 對于約瑟夫問題,從1開始往后報數。顯然,當報數報到(n-1)*k時,必然有n-1個人離開,所以,最后一人報數必然是(n-1)*k+1。因此,約瑟夫問題可以描述為:編號為1到n的n個人,按順序圍成一圈,從1往后開始報數,報k的倍數的人離開。問:最后報數為(n-1)*k+1的是哪一個。 順推法的基本思想是,從1到n逐個分析當前報數為m時,最后一次報數能否達到(n-1)*k+1。分析如下: (1)當m為k的倍數時,m即為最后一次報數。 (2)當m不為k的位數時,此時,必有m/k個人不參與報數,即參數報數的人數為n-m/k個。所以,下輪的報數必然是m+(n-m/k)。于是,當前報數為m,求最后一次所報數的算法如下: int lastNum(int n,int k,int m){ while(m%k!=0&&m<(n-1)*k+1) m=m+n-m/k; return m; } 求解約瑟夫問題的主程序為: int main(){ 定義變量,輸入n,k } for(i=1;i<=n;i++) //逐個判斷最后一個報數能否達到(n-1)*k+1 if(lastNum(n,k,i)>=(n-1)*k+1) { 輸出i,程序結束 } } 約瑟夫問題,可歸結為n個人,從1開始順序報數,每報k的倍數的離開,問哪個數報到(n-1)*k+1。倒推法的基本思想是:從(n-1)*k+1倒推到上一輪的報數值,繼續倒推到上一輪的報數值,直到報數值在1到n的范圍中。 核心問題:當前報數為m,問上一輪的報數為多少解法一:設上輪報數為x,顯然,x不為k的倍數,可將x表示為: 此時,已有p個人不參與報數。所以, 將式(1)代入式(2)可得: m=p*k+r+n-p,進一步可化為: m-n-1=p*(k-1)+(r-1),其中:r-1:0…(k-2) 于是:p=(m-n-1)/(k-1); r=(m-n-1)%(k-1)+1 所以,當前報數為m,求上輪報數值的算法如下:int preNum(int n,int k,int m){ int x,p,r; p=(m-n-1)/(k-1); r=(m-n-1)%(k-1)+1; x=p*k+r; return x; } 求解約瑟夫問題的主程序為: int main(){ 定義變量,輸入n,k num=(n-1)*k+1; while(num>n) num=preNum(n,k,num); 輸出num } 解法二:由式(2)得: 遞歸法的基本思想是將n個人的約瑟夫問題轉化為n-1個人的約瑟夫問題。將n個人圍成一圈,從1開始報數,報k的倍數的人出局的約瑟夫問題記為f(n,k)。遞歸法的基本思想便是尋找f(n,k)與f(n-1,k)之間的關系。核心問題是:n>1時,已知f(n-1,k)=m求f(n,k)。 對f(n,k)的求解分析如下,第一個出局的編號記為a1。 (1)當n>=k時,a1=k。a1出局后,剩余的n-1個便形成了n-1個的約瑟夫問題。由于f(n-1,k)=m,所以,f(n,k)的解應該是a1往后m個。由于a1+m的值可能大于n,所以,必須將a1+m通過取余運算轉化為1到n的范圍。 于是:f(n,k)=(a1+m-1)%n+1,即:f(n,k)=(k+m-1)%n+1。 (2)當 n f(n,k)=(a1+m-1)%n+1=((k-1)%n+m)%n+1 即:f(n,k)=(k+m-1)%n+1; 綜上可得:無論n與k的大小關系如何,均有f(n,k)=(k+m-1)%n+1。 也就是,當n>1時,f(n,k)=(k+f(n-1,k)-1)%n+1; 遞歸法算法如下: int f(int n,int k){ if(n==1)return 1; else return(k+f(n-1,k)-1)%n+1; } 求解約瑟夫問題的主程序為: int main(){ 輸入 n,k; p=n-m+x,代入式(1)得: x=(n-m+x)*k+r,展開得: x=n*k-m*k+k*x+r m*k-n*k-1=x*(k-1)+(r-1) x=(m*k-n*k-1)/(k-1) 于是算法描述為: int preNum(int n,int k,int m){ return(m*k-n*k-1)/(k-1); } 輸出f(n,k); } 數組標記法直觀易懂,但運行效率低。利用鏈式結構的查找與刪除,在運行時間上略有改進。但未有實質性的改進與突破。遞歸法雖然代碼簡單,但其運行機理是借助于棧的存儲,運行時所占用的內存資源卻是巨大的。而遞推法尤其倒推法則是解決約瑟夫問題較為有效的方法。表1是約瑟夫問題不同方法的運行時間對比(k值取999)。從表1中可以看出。倒推法效率最高。數組標記法效率最低。 表1 約瑟夫問題算法運行時間對比(單位:毫秒) 約瑟夫問題是計算機算法設計中的經典問題,是訓練編程能力較為理想的案例。對約瑟夫問題的歸納總結有助于強化對各種算法的理解,提高算法的應用能力。2.2 鏈式查找法
2.3 順推法
2.4 倒推法


2.5 遞歸法
3 約瑟夫問題解決方法對比
4 結語

