類聲子晶體結構對超聲塑料焊接工具橫向振動的抑制?

趙甜甜 林書玉? 段祎林

1)(陜西師范大學,陜西省超聲重點實驗室,西安 710119)

2)(西安石油大學理學院,西安 710065)

(2018年6月12日收到;2018年9月30日收到修改稿)

1 引 言

超聲焊接是大功率超聲的主要應用之一,在汽車工業、航空及航天等領域具有廣泛的應用[1].換能器和工具頭是超聲焊接系統的重要組成部分.對于不同的焊接對象,需要使用不同的工具頭.就較大的塑料焊接部件而言,需要使用大尺寸的焊接工具對其進行焊接.林書玉和張福成[2]曾研究了大尺寸焊接工具,發現其在換能器的激發下,工具頭將會產生縱向振動和橫向振動的耦合效應.橫向振動會使工具頭輻射面位移不均勻,從而影響焊接效果.因此,必須采用一定的方法抑制工具頭的橫向振動,提高超聲塑料焊接系統的工作效率,優化焊接效果.本文設計的焊接工具頭采用類聲子晶體結構,該結構可對工具頭的橫向振動進行有效抑制.

類聲子晶體結構不同于理想聲子晶體,理想的聲子晶體模型一般認為在非周期方向具有無限尺寸,本文的聲子晶體結構在非周期方向尺寸有限.溫熙森等在《聲子晶體》專著中將這類結構稱為類聲子晶體結構或典型聲子晶體結構[3?6].當彈性波穿過聲子晶體時,由于受到周期性排列材料的影響,會與聲子晶體的周期結構發生相互作用,從而產生帶隙(帶隙頻率范圍內的彈性波無法傳播)[7?10].而對于類聲子晶體結構而言,可用其振動帶隙代替彈性波帶隙[11],因此類聲子晶體結構的材料在減振降噪、聲濾波器、新型換能器等方面均有著非常廣泛的應用[12?15].本文就類聲子晶體結構在大尺寸超聲塑料焊接工程中的應用進行研究.

2 大尺寸矩形工具焊接系統

超聲焊接系統的核心部件,包括換能器、變幅桿、工具頭.對于大尺寸塑料焊接部件,焊接時要使用大尺寸工具頭,而工具頭形狀的選取要視焊接部件而定.本文針對形狀為矩形六面體的大尺寸工具頭進行研究.一般情況下矩形工具頭超聲塑料焊接系統如圖1所示:由夾心式換能器與大尺寸金屬工具頭組成.在實際工作中,為了使換能器高效工作,要求工具頭的諧振頻率等于換能器的激發頻率[16?18].圖1中工具頭的高度z方向與寬度y方向上的尺寸較大,厚度x方向的尺寸較小且與高度z和寬度y相差較大,因此在換能器的激勵下,將會產生z方向和y方向的耦合振動.z方向的縱振動是焊接工程中需要的,y方向的橫振動會導致焊接工具的輻射面位移不均勻,因此必須抑制y方向的橫振動.本文應用聲子晶體的帶隙理論對大尺寸矩形超聲波塑料焊接工具頭的耦合振動進行研究,把工具頭設計為寬度方向的聲子晶體周期結構,使得工具頭的橫向振動帶隙頻率接近于換能器振動系統的縱向振動共振頻率,從而達到抑制振動系統在寬度方向的橫向振動的目的.

圖1 大尺寸矩形工具頭超聲塑料焊接系統示意圖Fig.1.Schematic of large-size rectangular tool ultrasonic plastic welding system.

3 矩形六面體的三維耦合振動理論

由彈性動力學理論可知,在忽略振動體剪切、扭轉和彎曲振動的前提下,矩形板內任意一點的軸向應力和應變之間的關系為[19]:

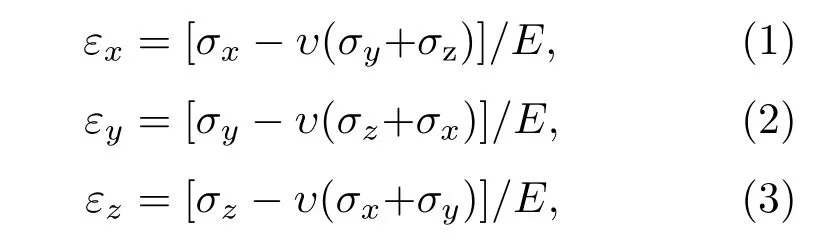
上式中ν和E分別表示矩形六面體材料的泊松系數和彈性模量;εx,εy,εz,σx,σy,σz表示沿坐標軸X,Y,Z方向的應變與應力.令:

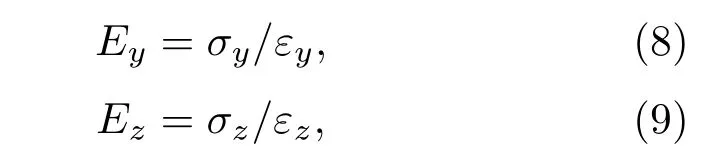
上式中q1,q2,q3分別表示X軸和Y軸、Y軸和Z軸、Z軸和X軸縱振動之間的耦合系數;Ex,Ey,Ez為軸向表觀彈性系數.根據(4),(5),(6)式可得q1q2q3=1.

圖2 矩形六面體示意圖Fig.2.Schematic of rectangular hexahedron.

將(4)—(9)式代入(1)—(3)式可得:

根據表觀彈性法原理,可把大尺寸塑料超聲焊接工具的振動看成是沿振動工具軸向的三個相互垂直的一維縱振動的耦合振動,同時沿各軸的一維縱振動可等效成彈性系數分別是Ex,Ey,Ez的一維細長棒的縱向振動.在矩形六面體(圖2)六個表面均為自由的前提下,可得到大尺寸矩形振動工具三維耦合振動時各方向的頻率方程:

根據(4)—(6)式以及(16)—(18)式消去耦合系數q1,q2,q3可得大尺寸超聲塑料焊接工具耦合振動的總體頻率方程:

上式中,A=C2π2/ω2,C2=E/ρ.由(19)式可知,大尺寸塑料焊接工具耦合振動的諧振頻率由給定工具的材料和尺寸決定.

本文設計的換能器及工具頭的高度均為110 mm,換能器的半徑為11 mm,工具頭厚度和寬度分別為22,280 mm.由于工具頭的厚度與高度及寬度相差較遠,因此不會產生x方向的耦合振動.其橫向尺寸ly相比于縱向尺寸lz較大,且兩尺寸在數值上可相比擬,因此受泊松效應的影響,工具頭將會產生嚴重的沿寬度方向的橫向振動.為了保證焊接系統的工作效率,必須將工具頭的結構加以改進,將橫向振動的影響降到最低.本文設計的工具頭采用類聲子晶體結構,該結構存在橫向振動帶隙,可將其橫向振動進行抑制.

4 類聲子晶體結構模型及振動帶隙

聲子晶體是由兩種(或以上)彈性材料按一定方式排列組成的周期性結構.其顯著特征是存在彈性波帶隙,即在一定頻率范圍內的彈性波在聲子晶體中無法傳播.理想的聲子晶體其能帶結構可用解析法計算,常用的解析法有傳遞矩陣法、平面波展開法、集中質量法等[20?23].而對于周期數有限、尺寸有限的類聲子晶體結構,解析法則不再適用.

本文將超聲焊接系統中的工具頭設計為一維氣-固型類聲子晶體(即空氣散射體周期性分布在金屬固體基體中),因為該結構的模型在實際生產中較易實現,同時還能達到較好的振動抑制效果.由于解析法已不再適用于有限周期的類聲子晶體結構,本文用Comsol Multiphysics有限元軟件對工具頭橫向振動帶隙進行計算.Comsol Multiphysics有限元軟件計算帶隙已經被廣泛應用,陳阿麗[24]、郭鳳丹[25]用其計算準周期聲子晶體板帶隙時已經證實該方法與平面波展開法計算出的一維理想聲子晶體板的頻散曲線非常符合.文獻[26]研究了一維聲子晶體的振動實驗,我們用Comsol Multiphysics有限元軟件建立與文獻[26]中完全一樣的幾何模型,即鋁和聚甲基丙烯酸甲酯(PMMA)組成的周期數為5.5的一維聲子晶體桿,并計算其振動帶隙,結果和文獻[26]中的實驗結果一致.因此,我們總結得出利用該有限元軟件來計算一維類聲子晶體結構的振動帶隙是有效的.

本文設計的類聲子晶體結構工具頭的單包模型如圖3所示:晶格常數a=70 mm,基體材料的高度b=110 mm,散射體空氣層的寬度c=10 mm,高度d=60 mm.基體和散射體的厚度e均為22 mm.

圖3 聲子晶體結構的單包模型Fig.3.Single-package model of phononic crystal structure.

實際工程應用中,超聲塑料焊接工具由多個單包在工具頭寬度方向依次排列而成,所以該焊接工具是水平方向上的一維類聲子晶體.本文中類聲子晶體工具頭由4個單包在寬度方向排列而成,因此計算時選取4個在寬度方向依次排列的單包進行建模,即周期數為4.在工具頭的左端施加大小為1方向平行于輻射面的加速度,通過MUMPS求解器計算,得到超聲塑料焊接工具頭寬度方向的加速度幅值隨頻率的變化關系即加速度響應曲線,如圖4所示.

圖4表示加速度在寬度方向的幅值隨頻率的變化關系,其幅值小于1的頻率范圍,我們稱之為橫向振動帶隙.因此,將工具頭的縱向共振頻率設計在橫向振動帶隙內,可以有效抑制其橫向振動.加速度響應曲線中衰減峰處對工具頭橫向振動抑制最為明顯,因此,要盡量將焊接系統的共振頻率設計在加速度響應曲線的衰減峰頻率附近.

為了探究散射體空氣層的寬度是否對帶隙有影響,我們比較不同寬度空氣層對應的帶隙分布,將散射體空氣層的高度固定為60 mm不變,改變其寬度分別為5,10,15 mm,對應的工具頭振動帶隙分布如圖5所示:藍色點虛線、青色實線以及紅色虛線分別代表散射體尺寸為5 mm×60 mm,10 mm×60 mm以及15 mm×60 mm時的加速度響應曲線.

圖4 聲子晶體結構寬度方向的加速度響應Fig.4.Acceleration response in the width direction of the phononic crystal structure.

圖5 不同寬度散射體的加速度響應Fig.5.Acceleration response of scatterers of different widths.

從圖5可知,不同寬度的散射體,其振動帶隙的頻率范圍不同.隨著寬度的增加,帶隙的起始頻率和截止頻率會有所減小.所以,可通過改變散射體的尺寸,使帶隙的頻率范圍發生改變.由于散射體空氣層尺寸的改變不僅會影響帶隙頻率,工具頭的振動模態以及系統的共振頻率均會受到影響.因此,在焊接系統的設計中,我們要用最佳的設計方式,使焊接系統的工作性能最好.

5 計算結果及分析

由圖4加速度響應曲線可知類聲子晶體結構工具頭在頻率0—30 kHz范圍內,存在振動帶隙.超聲塑料焊接工程中,換能器的激發頻率一般在20 kHz左右,為了使大尺寸工具頭的橫向振動得到較好的抑制,同時使振動系統高效工作,我們在設計焊接系統時,應使其縱向共振頻率接近于換能器的激發頻率,該頻率位于工具頭橫向振動帶隙內且接近于加速度響應曲線衰減峰值處所對應的頻率.本文設計的大尺寸焊接系統的換能器及工具頭的高度均為110 mm,換能器的半徑為11 mm,工具頭厚度和寬度分別為22,280 mm,散射體空氣層的寬度及高度分別為10,60 mm,厚度為22 mm.未采用氣固型聲子晶體結構的工具頭,其在換能器激勵下,振動模態如圖6(a)所示.將工具頭優化為一維氣-固型類聲子晶體結構時,其振動模態如圖6(b)所示.

從圖6(a)和圖6(b)可明顯看出:系統的縱向工作頻率設計為21940 Hz時,采用類聲子晶體結構的工具頭,其橫向振動可被很好地抑制因為該工作頻率恰好位于工具頭橫向振動的帶隙范圍內,且接近于圖4加速度響應曲線中第二帶隙衰減峰值處的頻率值.為了比較圖6(a)和圖6(b)對應模態的工具頭輻射面位移,做出兩圖中輻射面縱向振動相對位移分布,如圖7所示.

圖6 工具頭振動模態 (a)未采用聲子晶體結構;(b)具有聲子晶體結構Fig.6.Vibration mode of the tool:(a)Vibration modes of the tool without phononic crystal structure;(b)vibration mode of the tool with phononic crystal structure.

圖7 輻射面位移分布圖Fig.7.Displacement distribution of radiation surface.

圖7中藍色虛線是圖6(a)未采用聲子晶體結構的工具頭振動模態對應的輻射面位移,紅色實線為圖6(b)采用聲子晶體結構工具頭的振動模態對應的輻射面位移.由圖7分析可知:類聲子晶體結構在抑制工具頭橫向振動的同時,還使得工具頭輻射面的位移增大并且趨于均勻化.

6 結 論

本文利用聲子晶體帶隙理論以及耦合振動理論設計了氣-固型類聲子晶體結構大尺寸矩形工具頭塑料焊接系統,將該系統的縱向共振頻率設計在工具頭橫向振動的帶隙范圍內,工具頭的橫向振動能夠被有效抑制.且采用聲子晶體結構的大尺寸工具頭,其輻射面位移相比于未采用聲子晶體結構的工具頭輻射面位移有所增加且趨于均勻化,大大優化了焊接效果,提高了焊接系統的工作效率,可滿足實際工程中的需要.