Majorana fermions induced fast-and slow-light in a hybrid semiconducting nanowire/superconductor device

Hua-Jun Chen(陳華俊), Peng-Jie Zhu(朱鵬杰), Yong-Lei Chen(陳詠雷), and Bao-Cheng Hou(侯寶成) 232001

We investigate theoretically Rabi-like splitting and Fano resonance in absorption spectra of quantum dots (QDs)based on a hybrid QD-semiconducting nanowire/superconductor(SNW/SC)device mediated by Majorana fermions(MFs).Under the condition of pump on-resonance and off-resonance, the absorption spectrum experiences the conversion from Fano resonance to Rabi-like splitting in different parametric regimes. In addition,the Fano resonances are accompanied by the rapid normal phase dispersion,which will indicate the coherent optical propagation. The results indicate that the group velocity index is tunable with controlling the interaction between the QD and MFs,which can reach the conversion between the fast-and slow-light. Fano resonance will be another method to detect MFs and our research may indicate prospective applications in quantum information processing based on the hybrid QD-SNW/SC devices.

Keywords: majorana fermions, Fano resonance, slow and fast light, hybrid semiconducting/superconductor device

1. Introduction

Majorana fermions (MFs) have witnessed significant progress over the past decade in solid state systems for their potential applications in topological quantum computation and quantum information processing[1—7]due to the fact that they obey non-Abelian statistics. Although MFs were proposed originally as a model for neutrinos,the analogous Majorana zero modes have been observed in condensed matter systems,[8]such as hybrid semiconducting nanowire/superconductor (SNW/SC) structures,[9—12]ferromagnetic atomic chains on a superconductor,[13]ironbased superconductor device,[14]topological superconductor devices,[15,16]and topological insulator structure.[17]In order to observe Majorana-like signatures, several significant experimental schemes have been proposed, including the zerobias peaks(ZBPs)in tunneling spectroscopy,[9—13]the Josephson effect,[18]the Coulomb blockade spectroscopy,[15]and the spin-resolved measurements.[19]

On the other hand, due to the significant progress in modern nanoscience and nanotechnology, artificial atoms,i.e., quantum dots (QDs),[20—25]manifest the attractive intermediary for probing MFs both theoretically[26—30]and experimentally.[31]However, in the detection of MFs with QDs in the electrical domain, QDs are always considered as only a resonant level.[26—30]Different from the previous schemes for probing MFs, we have presented an optical scheme for probing MFs with a QD considered as a twolevel system (TLS) and driven by the optical pump-probe technology,[32—35]which may provide a potential supplement for probing MFs. However,Rabi splitting and Fano resonance induced by MFs in optical domain based on a hybrid QDSNW/SC device have not yet been explored to the best of our knowledge,needless to say reaching the coherent optical propagation,such as the fast-and slow-light effects.

In this paper,firstly we demonstrate that the probe absorption spectra of the QD show the switch from Rabi-like splitting to Fano resonance induced by MFs for different detuning regimes in the hybrid QD-SNW/SC device, which can be illustrated using the interference effect with the dressed state theory. Under the condition of pump on-resonance,the probe absorption spectra present a distinct Rabi splitting behavior with increasing the QD-MFs coupling strengthβ,which manifests a strong interaction of the QD and MFs,and the width of the splitting is 2β, which indicates an approach to determine the QD-MFs coupling strength. In the pump off-resonance,the probe absorption spectra can show a series of asymmetric Fano line shapes,and the Fano resonances are tunable under different parametric regimes, such as the Majorana-pump field detuningΔMand the exciton-pump field detuningΔc. As Fano resonances are characterized by a rapid steeper dispersion, the light pulses can be accelerated and decreased significantly, which correspond to the negative and positive dispersions, respectively, and then reach the fast and slow light effect. Secondly, we investigate the coherent optical propagation properties, i.e., the fast and slow light effect via the group delay of the probe field around the transparency window accompanied by the steep phase dispersion. The results show that a controllable fast-to-slow light propagation can be reached with manipulating the parametric regimes.

2. Model and method

The system under consideration is sketched in Fig. 1,where a QD coupled to a near by MFs appearing in the hybrid SNW/SC device,[9—12]and the Hamiltonian is given by[26—30,32—35]

where the first term indicates the Hamiltonian of the QD with the exciton frequencyωex. In the previous works for probing MFs, the QD is consider as a single resonant level with spinsinglet state,[26—30]here we consider that the QD is a TLS with the ground state|0〉and the single exciton state|1〉, which is described by the pseudospin operatorsSzandS±with the commutation relations[Sz,S±]=±S±and[S+,S?]=2Sz.

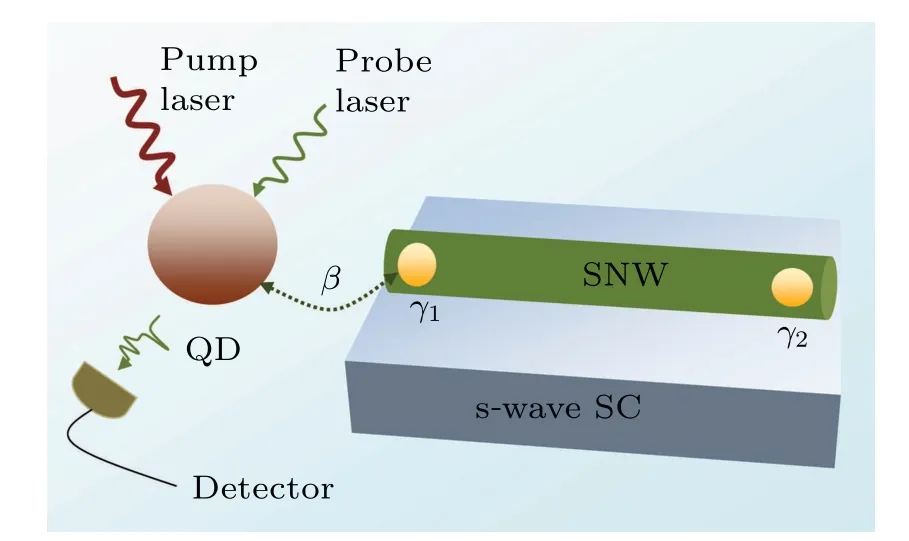
Fig. 1. The schematic of the hybrid QD-SNW/SC device, in which a QD driven by a pump field and a probe field coupled to a nearby MF in the end of SNW.

The second term is the interaction of the two MFs in the end of SNW in the hybrid SNW/SC device. To describe MFs,we introduce the Majorana operatorsγ1andγ2with the relationγ?=γandγ2=1 as they are their own antiparticles.Here,εM=ωM～e?l/ξis the coupling energy withlbeing the length of the SNW andξthe superconducting coherent length with Majorana frequencyωM. If the lengthlof the SNW is large enough, we can find the coupling energyεM～e?l/ξ ～0. Thus,we need to discuss the two cases,i.e.,εM/=0 in terms of coupled Majorana edge states,andεM=0 in terms of uncoupled Majorana edge states.

The third gives the nearby MFsγ1coupled to the QD with the coupling strengthβ, and the coupling strength is related to the distance of the QD and SNW/SC device. For simplicity, we introduce the regular fermion creation and annihilation operatorsf?andfwith the anti-commutative relation=1,thus,according to the relation ofγ1=f?+fandγ2= i(f??f), Majorana operatorγcan be transformed into the regular fermion operatorf. Then the third term reduces to i(S?f??S+f) with neglecting the non-conservation terms of energy i(S?f ?S+f+)based on the rotating wave approximation.[36]

The last two terms indicate the interactions between the QD and two laser fields including a strong pump field with frequencyωpand a weak probe field with frequencyωssimultaneously irradiating to the QD,whereμis the electric dipole moment of the exciton,εpandεsare the slowly varying envelope of the pump field and probe field,respectively. In a frame rotated to the frequencyωpof the pump field, Eq. (1) can be rewritten as

whereΔp=ωex?ωpindicates the exciton-pump field detuning,ΔM=ωM?ωpmeans the Majorana-pump field detuning, andδ=ωs?ωpgives the probe-pump detuning. Here,Ωp=μεp/is the Rabi frequency of the pump field. According to the Heisenberg equation of motion i=[ρ,H](ρ=Sz,S?,f),we can obtain the Heisenberg—Langevin equations of the operators with the corresponding noise and damping terms as follows:

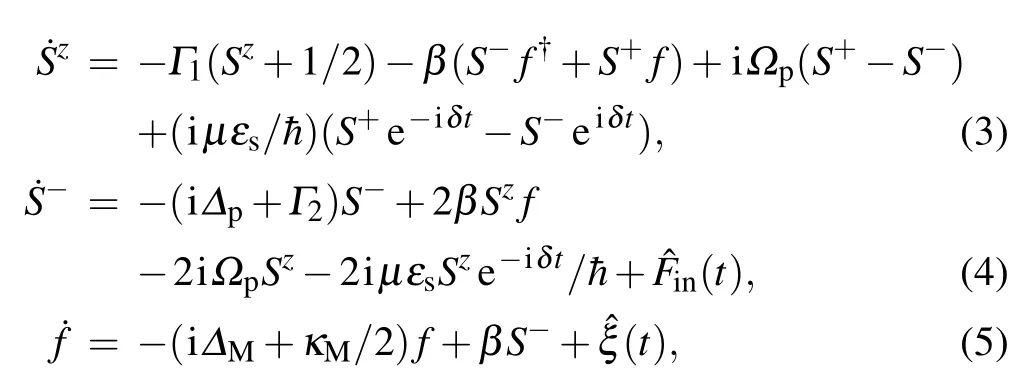
whereΓ1(Γ2)is the exciton relaxation rate(exciton dephasing rate), andκMis the decay rate of the MFs.is theδcorrelated Langevin noise operator with zero mean, andξis Langevin force arising from the interaction between the Majorana modes and the environment.

Morning came, and the king got up, pale and sulky, and, after learning from the hermit which path to take, was soon mounted and found his way home without much difficulty

We introduce the perturbation theory:ρ=ρ0+δρ,whereρindicates the operatorsSz,S?, andf, thenρ0(i.e.,,S0,andf0)means the steady parts,andδρ(i.e.,δSz,δS?,andδ f) indicates the fluctuation ones. Substituting the perturbation method into Eqs. (3)—(5) we obtain the steady state solutions of the variables as follows:

which determine the steady-state population inversion (w0=)of the exciton as follows:

where, andΞ3=. As all the pump fields are assumed to be sufficiently strong, all the operators can be identified withtheir expectation values under the mean-field approximation〈Qc〉=〈Q〉〈c〉,[37]after being linearized by neglecting nonlinear terms in the fluctuations,the H-LEs for the expectation values are

In order to solve the equation set of the above H-LEs, we make the ansatz[38]〈δρ〉=ρ+e?iδt+ρ?eiδt. Solving the equation set and working to the lowest order inεsbut to all orders inεp, we obtain the linear optical susceptibility aswithand then the dimensionless linear susceptibilityχ(1)(ωs) is given by

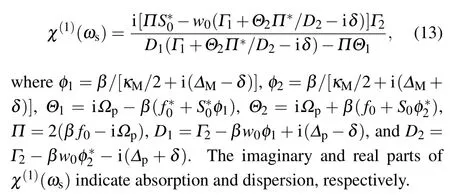
According to the light group velocity[39,40]υg=c/[n+ωs(dn/dωs)],wheren ≈1+2πχ(1)

eff,we obtain

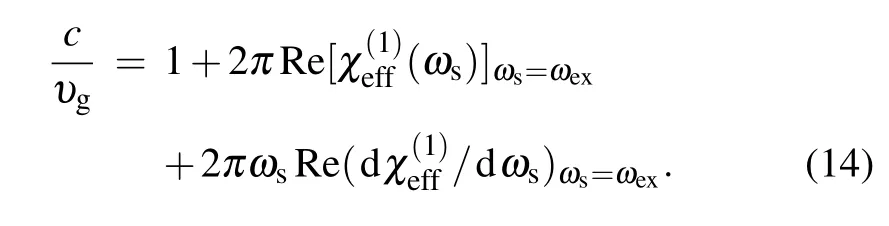
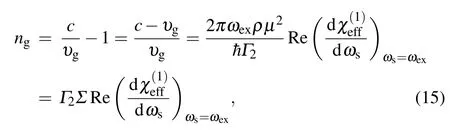
where. One can observe the slow light ifng>0, and the superluminal light whenng<0.[41]The parameter values used in the paper:[9—12,35,42]the QD-MFs coupling strengthβ= 0.1 GHz, the decay rate of the MFsκM= 0.1 MHz,Γ1= 0.3 GHz,Γ2= 0.15 GHz, and=0.005(GHz)2.

3. Results and discussion

Firstly, we discuss the case of uncoupled Majorana edge state, i.e.,εM= 0 (orΔM= 0) under the condition of the exciton-pump field detuningΔp=0,and the Hamiltonian describing the coupling between the QD and nearby MFs reduces toHint=i(S?f??S+f). Then the absorption spectra will display the symmetric splitting due to the fact that the coupled Hamiltonian is analogical to the J—C Hamiltonian of the standard model. In Fig. 2, we plot the probe absorption (the imaginary part of the dimensionless susceptibility i.e.,Imχ(1))versus the probe-exciton detuningΔs=ωs?ωexfor several different MF-QD coupling strengthsβ. Obviously,in the case ofβ=0,i.e.,without MF-QD coupling,the absorption spectrum shows a lorentz peak. However, when the MF-QD couplingβis considered,the absorption spectra display an evident splitting behavior, and the splitting is enhanced prominently with increasing the MF-QD couplingβfromβ=0.1 GHz toβ=0.6 GHz. In addition,the splitting in the absorption spectrum is symmetric, which is like the vacuum Rabi splitting,and the width of splitting is 2β, and the peak splitting manifests the strong interaction between MF and QD.The physical origin of the results comes from the coherent interaction of the QD and MFs,and we introduce the dressed state theory to explain this physical phenomena.[35]Because QD is considered as TLS with the ground state|0〉and exciton state|1〉, when QD is coupled to the nearby MFs,QD will be modified by the number states of the MFsnMinducing the Majorana dressed states|0,nM〉,|0,nM+1〉,|1,nM〉,|1,nM+1〉. The left sharp peak of splitting in the absorption spectra indicates the transition from|0〉to|1,nM〉,and the right sharp peak is due to the transition of|0〉to|1,nM+1〉. On the other hand,we find that the absorption dip will reach zero atΔs=0 whenβ /=0,that is to say,the input probe field is transmitted completely without any absorption, which is very similar to electromagnetically induced transparency(EIT)[43]inΛ-type atoms systems.Since EIT can induce slow light,the hybrid QD-SWN/SC system can also reach slow light effect.

Fig. 2. The probe absorption versus the probe-exciton detuning Δs =ωs ?ωex for several different MF-QD coupling strengths β. The other parameters are Γ1 =0.3 GHz, Γ2 =0.15 GHz, κM =0.1 MHz,=0.005(GHz)2,ΔM=Δp=0.

In Fig. 3(a), we investigate the dispersion (the real part of the dimensionless susceptibility, i.e., Reχ(1)) as a function ofΔsfor several different MF-QD coupling strengthsβatΔp=0. It is obvious that the dispersion exhibits the negative steep slope atΔs=0 forβ=0(the black curve in Fig.3(a)),which combines the lorentz peak atΔs=0 in Fig. 2, leading to the fast light effect. However, ifβ /=0, the dispersion will exhibit the positive steep slope atΔs=0,which combines the zero absorption atΔs=0 in Fig. 2, resulting in the slow light effect. It is analogous to EIT[43]inΛ-type atoms systems,a transparency window will lead to the slow light effect,in our system the MF-QD coupling also results in the analogous zero absorption transparency window, which is accompanied with the rapid normal phase dispersion, indicating the coherent optical propagation, such as the fast and slow light effect. No matter what regimes result in the zero absorption,when a transparency window is observed, the slow light or fast light will be induced. In our hybrid coupled QD-SNW/SC system,when the transparency appears in the absorption spectrum,the slope around transparency window of the dispersion will experience the conversion between the negative to positive. The positive steep slope of dispersion will induce the positive group velocity index,i.e.,ng>0,then the slow light phenomenon will appear in the system. On the contrary, if the dispersion shows the negative steep slope, the group velocity index will be negative, i.e.,ng<0, as a result the fast light will be achieved. In Fig. 3(b), we plot the group velocity indexngof probe laser versus QD-MF coupling strengthβunder the condition ofΔM=0 andΔp=0. We can find that the group velocity indexngexperiences the positive—negative—positive change,which corresponds to the slow-fast-slow light.In Fig. 3(c), we also give the group velocity indexngas a function of Rabi frequencyin the case ofβ=0. As the dispersion shows a negative steep slope atΔs=0 forβ=0 as shown in the black curve in Fig. 3(a), which combines a lorentz peak in Fig.2 resulting in the fast light effect. Furthermore, the group velocity indexngvaries significantly around=0.1(GHz)2. In Fig.3(d),we consider the case ofβ /=0,due to the fact that the dispersion exhibits the positive steep slope atΔs=0, and then the group velocity indexngis positive with varying the Rabi frequency,therefore,the slow light effect can be obtained.

Fig.3. (a)The dispersion as a function of Δs for several different MF-QD coupling strengths β at ΔM=Δp=0. (b)The group velocity index ng versus QD-MF coupling strength β under the condition of ΔM=0 and Δp=0. (c)ng as a function of for β =0. (d)ng versus for β =0.1 GHz.

Secondly, we consider the coupled Majorana edge state,i.e.,εM/=0(orΔM/=0)still in the case ofΔp=0. In Fig.4,we display the probe absorption spectra versusΔsfor differentΔM,which experience the conversion from unsymmetrical splitting(Fano resonance like splitting)to symmetric splitting(EIT like splitting)to Fano resonance. Unlike EIT with symmetric splitting,the Fano resonance-like splitting is an asymmetry shape due to the fact that the scattering of light amplitude under the condition of EIT is not met and a detuning is introduced. Obviously,the absorption spectra show the Fanoresonance-like splitting underΔM/=0 due to the MF-QD interaction,and the Fano-like resonance will change into a symmetric EIT-like splitting atΔM=0.Furthermore,the evolution process of the two sharp unsymmetrical peaks varies significantly for different detuningΔM, and the amplitude intensity of the left peaks is enhanced and the right peaks are reduced with changingΔMfromΔM=?0.3 GHz toΔM=0.3 GHz.In addition,we find that the absorption spectra are asymmetricand a prominent avoided crossing phenomenon occurs in the system,[44]which is very different from the case ofΔM=0 in Fig. 2, where the absorption spectra split into a doublet with symmetrical splitting and each peak has equal strength. This behavior is attributed to the off-resonant coupling between the QD and MF.

Fig.4. The probe absorption spectra versus Δs for several different ΔM at the parameters of=0.005(GHz)2 and β =0.1 GHz.

Therefore, in Fig. 5, we further investigate the slow and fast light effect under the condition of the coupled Majorana edge state (ΔM/=0) for the case ofΔp=0. In Fig. 5(a), we plot the absorption and dispersion spectra for the fixed QDMF coupling strengthβ=0.1 GHz and the Rabi frequency=0.005 (GHz)2underΔM=?0.1 GHz, and the absorption shows a Fano resonance and the steep slope aroundΔs=0 in the dispersion changes significantly. Thus,in Fig.5(b),we further display the dispersion versusΔsfor several differentΔM, and the processes of evolutions of the dispersion are related to the coupled Majorana edge state. Here,we only consider the case ofΔM≤0. Figure 5(c)shows the group velocity indexngas a function of QD-MF coupling strengthβunder several differentΔM, and it is obvious thatngcan realize the conversion from fast to slow light. Comparing the condition ofΔM=0 withΔM/=0,we can see that the experience of the group velocity indexnginΔM=0 is salient from the condition ofΔM/=0. Because the parameterβcan be manipulated with controlling the distance between the QD and SNW/SC device,we can obtain fast-to-slow light(or vice versa)by controlling the parameterβin the system. In Fig. 5(d), we also present the group velocity indexngversusfor threeΔM. We obtain thatngexperiences the conversion from slow to fast to slow light atΔM=?0.1 GHz. However, ifΔM

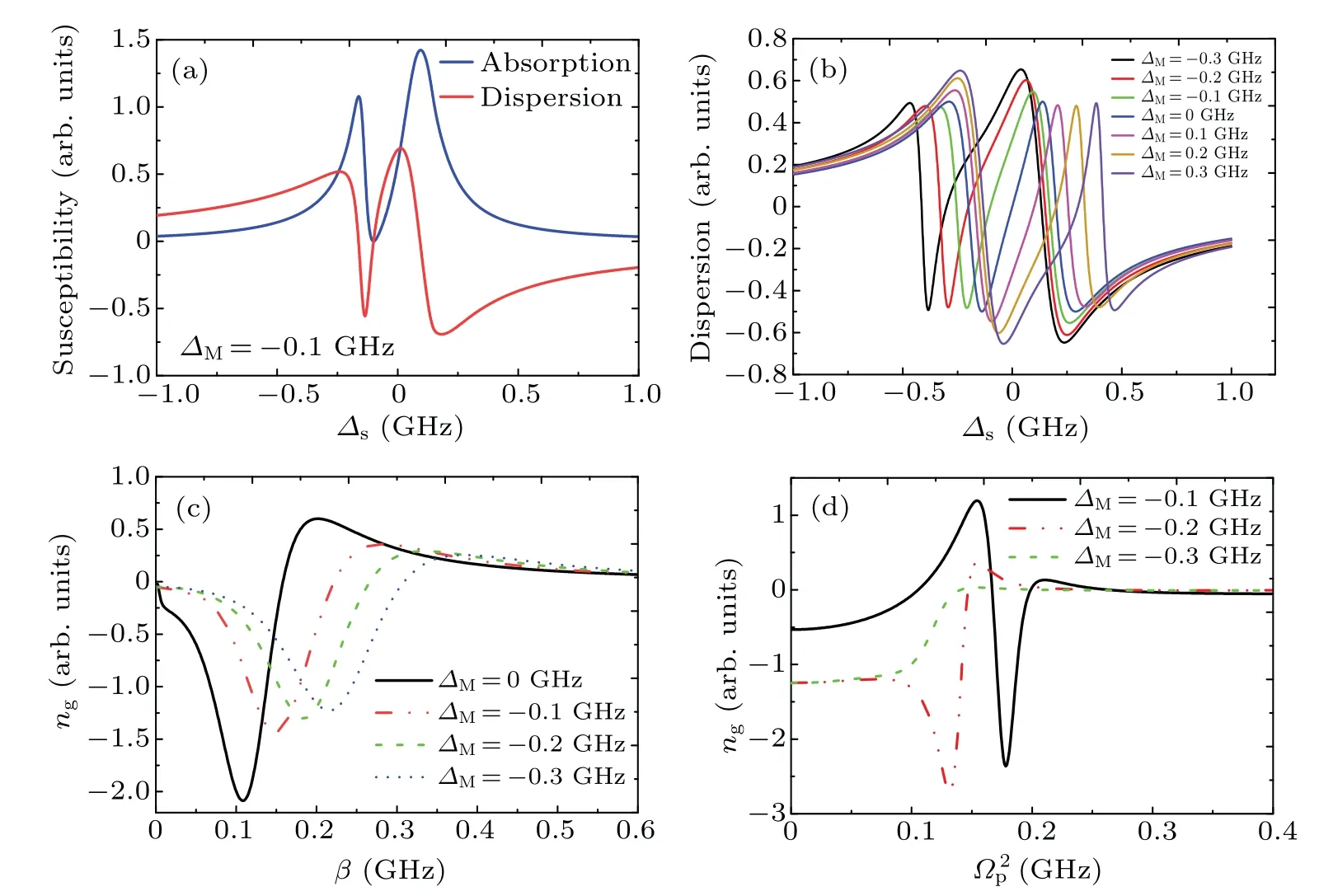
Fig.5. (a)The absorption and dispersion versus Δs at ΔM =?0.1 GHz. (b)The dispersion versus Δs for several different ΔM at Δp =0. (c)The group velocity index ng versus β for several different ΔM. (d)The group velocity index ng versus for several different ΔM.

In the above discussions,we only consider the case of the exciton-pump field detuningΔp=0,while under the condition ofΔp/=0, the Fano resonance will be altered tempestuously.In Fig.6(a),we plot the absorption spectra versusΔswith increasingΔpfromΔp=?0.3 GHz toΔp=0.3 GHz under the parameters of=0.005 (GHz)2andβ=0.2 GHz in the uncoupled Majorana edge state (ΔM=0), which experiences the conversion from Fano resonance to Rabi-like splitting to Fano resonance. Furthermore, besidesΔp=0, we find that the peaks in the absorption spectra present mirror symmetry atΔp=±Θ(Θindicates the definite numerical value)in the uncoupled Majorana edge state. Here, we takeΔp=?0.3 GHz andΔp=0.3 GHz as an example. IfΔp=?0.3 GHz, in the absorption spectrum as shown by the red curve in Fig. 6(a),the left peak locates atΔs=?0.4 GHz and the right peak locates atΔs= 0.1 GHz. However, ifΔp= 0.3 GHz, in the absorption spectrum as shown by the purple curve in Fig.6(a),the left peak locates atΔs=?0.1 GHz and the right peak locates atΔs=0.4 GHz. It is obvious that the left peak atΔp=?0.3 GHz is mirror symmetric with the right peak atΔp=0.3 GHz, and the right peak atΔp=?0.3 GHz is mirror symmetric with the left peak atΔp=0.3 GHz in the absorption spectra. When we change the condition ofΔM=0 intoΔM/=0,the Fano resonance manifests evident distinction compared withΔM=0 with varyingΔpfromΔp=?0.3 GHz toΔp=0.3 GHz as shown in Fig.6(b). We find that,with increasingΔpfromΔp=?0.3 GHz toΔp=0,the splitting width of the two peaks in the absorption spectra is reduced,i.e.,the absorption spectra is squeezed. However, with increasingΔpfromΔp=0 toΔp=0.3 GHz, the splitting width of the two peaks in the absorption spectra is enhanced,i.e.,the absorption spectra is stretched. No matter whetherΔM=0 orΔM/=0,we obtain that the full width at half maximum (FWHM) of the left peak is reduced and the FWHM of the right peak is enhanced in the absorption spectra with increasingΔpfromΔp=?0.3 GHz toΔp=0.3 GHz as shown in Figs.6(a)and 6(b).

Fig. 6. The absorption spectra versus Δs for several different Δp at ΔM =0. (b) The absorption spectra versus Δs for several different Δp at ΔM/=0. The other parameters are =0.005(GHz)2 and β =0.2 GHz.

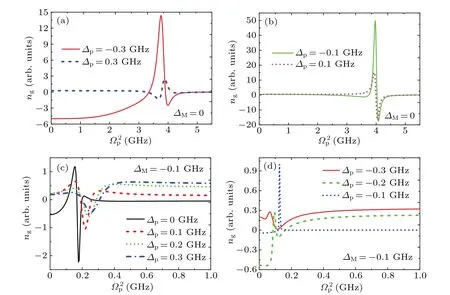
Fig.7. (a)and(b)The group velocity index ng versus for several Δp at ΔM=0 and β =0.2 GHz. (c)and(d)The group velocity index ng versus for several Δp at ΔM/=0 and β =0.2 GHz.

Then,on the other hand,we also demonstrate the coherent optical propagation properties for differentΔp/=0 andΔM/=0.In Fig. 7(a), we investigate the group velocity indexngas a function offorΔp=?0.3 GHz andΔp=0.3 GHz underΔM=0 at fixedβ=0.2 GHz. Figure 7(b)givesngversusforΔp=?0.1 GHz andΔp=0.1 GHz underΔM=0 at fixedβ=0.2 GHz. Compared Fig.7(a)with Fig.7(b)corresponding to Fig.6(a),we find that the group velocity indexngundergoes the conversion from advance to delay which corresponds to fast to slow light,and the conversion is more remarkable atΔp<0 than atΔp>0. In Fig. 7(c), we givengversusatΔM/=0 with increasingΔpfromΔp=0 toΔp=0.3 GHz,and Fig. 7(d) plotsngversusatΔM=?0.1 GHz forΔp<0,which corresponds to Fig. 6(b). We can obtain that the conversion from fast to slow light can reach in the two conditions,and compared with Fig. 7(c), the process of evolution of the conversion from fast to slow light is slightly different from Fig. 7(d). Thus, with controlling different detuning regimes,the fast-to-slow light,or vice versa,can be reached in our system.

In our system, we only consider the QD coupling to the nearby MFs, i.e., QD only couples to one MF due to the fact that it is confined by the length of the SNW and the superconducting coherent length.If QD is coupled to a pair of MFs,the results are significantly different. We have ever designed a hybrid QD-SNW/SC ring device,where QD is coupled to a pair of MFs,[34,35]and the results indicate that both the absorption spectra and the slow light(fast light)are enhanced observably compared with the results in this paper. In order to enhance the coherent optical properties(such as the linear or nonlinear optical phenomena)of QD induced by MFs,we have ever considered introducing a hybrid QD-nanoresonator system to investigate MFs induced coherent optical phenomena,[32,33]and the results manifest that both the linear or nonlinear optical phenomena induced by MFs are enhanced significantly due to the fact that the nanoresonator behaves as a phononic cavity,which enhances the linear and nonlinear optical effect. Therefore, to reach enhanced fast and slow light effect, the hybrid QD-nanoresonator system can be brought,and we will investigate the issue in the future work.

4. Conclusions

In summary, we have demonstrated the coherent optical propagation properties in a hybrid QD-SWN/SC device,which includes a QD driven by a pump field and a probe field coupled to a nearby MF in the hybrid SWN/SC system, and we investigate the absorption spectra of the probe field under both the conditions of the pump on-resonance (Δp= 0) and offresonance (Δp/=0). In the situation of pump on-resonance,the absorption spectra displays a Rabi-like splitting manifesting the strong interaction between the QD and MF. In pump off-resonance, the absorption spectrum experiences the conversion from Fano resonance to Rabi-like splitting in different parametric regimes. Moreover, the narrow transparency window(i.e.,the absorption dip approaches zero)in the absorption spectrum and the corresponding rapid phase dispersion allow for reaching the slow light effect. The results show that the group velocity index can be controlled by the QD-MF coupling,which can reach the conversion from fast to slow light.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant Nos. 11804004 and 11647001),the China Postdoctoral Science Foundation(Grant No. 2020M681973), and Anhui Provincial Natural Science Foundation,China(Grant No.1708085QA11).