淺談函數在經濟生活中的應用

陳鑫妍 華中師范大學第一附屬中學

一、引言

在社會經濟飛速發展的背景下，數學被廣泛應用于各個領域中。而函數是數學的基礎, 在實際生活中，很多經濟問題都可歸結為函數問題[1]，通過建立相應的函數關系,把問題轉化為數學模型，然后應用相應的數學理論來解決經濟實際問題。由此可見,在經濟生活中,處處離不開函數知識,函數與經濟分析緊密相連。下面就函數在經濟生活方面的應用做一些探析。

二、函數知識在經濟生活中的應用實例

（一）分段函數的應用

分段函數是一類常見的函數，此類函數蘊含著分類討論的數學思想。日常生活中的很多問題，例如水電費階梯計費、的士費按里程階段計價等都涉及到分類討論的問題，從而分段函數成為解決此類問題常用的數學模型。

案例1：優惠活動問題

隨著社會發展，消費成為拉動經濟發展的三駕馬車之一。很多消費者購物都會貨比三家，針對這樣消費心理，商家經常開展各種促銷活動。但是到底參與哪個方案買東西劃算，這就要利用分段函數[2]來計算并判斷。

例如：某淘寶網店實行優惠活動，規定一次購物付款總額：如果不超過300元，不予優惠；如果超過300元，但不超過500元，則按標價給予9折優惠；如果超過500元，500內部分按9折優惠第實施，超過500元部分給予8折。某人兩次購物，分別付款232元和466元。假設他只去購物一次，上述同樣商品，則應付款多少元？

問題分析：設未參加優惠活動前所有付款總數為x元，參加活動后應付款額為y元。

當0≤x≤300時，應付款額y=x；

當300＜x≤500時, 應付款額y=0.9x；

當500＜x時，應付款額y=500＊0.9+(x-500)＊0.8；

故得分段函數：

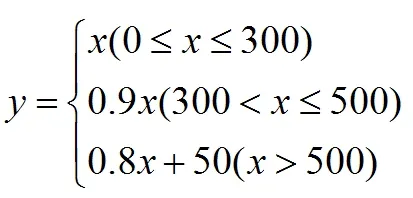
此人分開付款參加活動的話，總付款y=232+466=698元。

而根據分段函數公式可知，第二次付款的466是打8折后的價格，代入第三段則可求出未打折前的價格x=520。

則如果一次性付款，則總數x=232+520=752時，所以根據分段函數，參加活動后應付款額是y=651.6，比分次付款節約46.4元。可見利用分段函數提前分析規劃的話就能省下不少錢。

案例2：個人所得稅問題

納稅是每個公民應盡的義務，但近來某演藝界人士被爆偷稅漏稅丑聞，并罰以巨款，此事提醒公民一定要依法辦事。稅法規定，公民個人所得超過一定數額時，要依法繳納。那么個人如何計算自己的納稅額度？按照稅法建立一個簡單的分段函數就能算出納稅額度。

例如：新的《個人所得稅法》規定，公民每月薪金所得不超過5000元的部分不必納稅，超過5000元的部分為全月應納稅所得額。全月應納稅所得額不超過3000元的部分，所納稅率為3%；超過3000元至12000元的部分，所納稅率為10%；超過12000元至25000元的部分，所納稅率為20%。

（1）若三位納稅人每月薪金分別為4900元、9600元、19800元，則應繳納個人所得稅分別為多少？

（2）若某納稅人繳納個人得稅為150元，則此納稅人每月薪金為多少？

問題分析：設納稅人每月薪金為x元，應繳納個人所得稅為y元

當x≤5000時，y=0；

當5000＜x≤8000時，y=(x-5000)＊3%；

當8000＜x≤17000時，y=3000＊3%+(x-8000)＊10%；

當17000＜x≤30000時，y=3000＊3%+9000＊10%+(x-17000)＊20%；

故得分段函數：

則納稅人每月薪金為x=4900元，應繳納個人所得稅為y=0元；納稅人每月薪金為x=9600元，應繳納個人所得稅為y=0.1＊9600-710=250元；納稅人每月薪金為x=19800元，應繳納個人所得稅為y=0.2＊19800-2410=1550元。

當某納稅人應繳納個人所得稅為150元時，由分段函數看出第二段的最高繳稅額為90元，第三段的最高繳稅額為990元，則此納稅人每月薪金應在8000元至17000元之間，為（150+710）/0.1=8600元。

（二）指數函數的應用

指數函數是極具意義的數學工具，與生活中的實際問題有著非常廣泛的聯系。諸如細胞分裂、輻射衰減、銀行復利等問題都是涉及指數函數的例子。

案例3：存款利率問題

日常生活中，人們習慣于將富余資金進行投資理財，利息的計算中將會用到指數函數模型。

例如：假設存入的本金為10000元，每年的理財收益利率為20%。那么25年后的本利和是多少?

問題分析：按復利計算收益，本金為a元，每年的利率為r，設本利和為y，存期為x年，建立一個指數函數關系式：

將相應的數據代入該關系式就可得到25年后本利和y≈237萬。可見，若每年堅持投資1萬元，理財收益利率為20%時，25年之后將成為百萬富翁。因此，愛因斯坦說過，復利的威力比原子彈還可怕。

案例4：人口爆炸問題

人口問題是當今世界各國普遍關注的問題，認識人口的數量變化規律，可以為有效控制人口增長提供依據。

例如：表1是1950-1959年我國的人口數據資料。那么在大約1950年后68年（既2018年）我國人口數為多少？

表1 是1950-1959年我國的人口數據資料

問題分析：根據英國經濟學家馬爾薩斯模型[3]，自然狀態下的人口增長模型：y = y0ert。t指經過的時間，y0指t=0時的人口數，r 指人口的平均增長率。

令y0=55196，則我國在1950-1959年期間的人口增長率約為r=0.022，依公式可得億人口。

由此可見，改革開放初，如果不實行計劃生育，而讓人口自然增長，今天我國將面臨難以承受的人口壓力。當然計劃生育政策也顯現其負面效應，年輕人口數量減少，老年人所占比例增加，我國的人口年齡結構已經呈現出了顯著的老齡化特征。

（三）函數最值的應用

在生活中經常出現追求利潤最大、耗材最少、效率最高等現象，此類問題從數學角度上來看，就是求取函數的最大值，最小值問題，而利用函數求導即可解決此類問題[4]。

案例5：利潤最大問題

例如：某網店銷售甲、乙兩種商品，若初始投入 x 萬元資金，可分別獲利 M 萬元和 N萬元。若已知所投資金與獲利的關系式為，那么，今欲投資 10萬元銷售甲、乙兩種商品，如何分配在甲、乙兩種商品的投入資金，能使該網店獲利最大？ 能獲得多大利潤？

問題分析：該問題是二次函數最值的應用問題，同樣是按照題意寫出相關變量的函數表達式，然后可運用導數求最值。設投資x萬元給甲商品，則（10-x）萬元給乙種商品，所能獲得總利潤為y萬元，則根據題意得，，問題轉化為求該函數的最大值。

令y′=0，得：，則x=7.75。

此x為函數在定義區間內的唯一駐點，所以x=7.75是函數的極值點，故甲商品投資7.75萬元，乙商品投資2.25萬元，此時所獲最大利潤為3.06萬元。

案例6：最佳存、貸款利息問題

在經濟生活中，存、貸款利息問題，是最常見的問題。如何存款、貸款，才能收到最好的效益，這是一個最值問題，其間離不開函數求導的應用[5]。

例如：某理財公司，準備推出某種理財業務，假設吸引投資人獲得的存款量與存款利息成正比，理財公司貸款投資的收益率為20%。那么存款利息定為多少時，理財公司才能收到最大的貸款純收益?

問題分析：設存款總額為s，存款利率為x，則由題意吸引的存款總額s與x成正比，既s=ax(a 是正常數)。由于所有存款s都會被貸出以獲得收益，故設貸款總額也為s，則理財公司的貸款收益為：0.2s=0.2ax。

而這筆貸款 s要付給投資人的利息為 xs=ax2

從而理財公司的投資純收益為F(x)：

F(x)= 貸款收益-付給存戶的利息=0.2ax-ax2

x為函數在定義區間內的唯一駐點，所以x=0.1是F（x）的最大值點。故當存款利率為10%時，可創最高投資純收益。

三、小結

數學知識在經濟領域有著廣闊的應用舞臺，利用函數知識建立模型來解決實際問題很多時候特別有效。其能在日益變化的經濟生活中，科學描述和客觀分析經濟現象中因素與變量的關系，使得復雜的經濟現象變得簡單、清晰,為經濟分析帶來更加有效的計算方法，使經濟決策更加科學化，進而促進社會的可持續發展。