基于GNSS雙差定姿的區間列車軌道占用判別方法研究

王 迪， 陳光武， 劉射德， 楊 揚

(1. 蘭州交通大學 自動控制研究所，甘肅 蘭州 730070； 2. 甘肅省高原交通信息工程及控制重點實驗室， 甘肅 蘭州 730070)

列車定位作為列車運行控制的基礎，CTCS-4級列控系統要求列車自主獲取定位位置信息，減少傳統的軌旁設備，以提高鐵路運輸效率并減少建設維護成本[1]。為實現列車在區間的安全行駛、準確生成行車許可，列車運行控制系統需要準確地獲取列車位置信息并確定在軌道中的占用情況。這給列車定位精度提出了更高的要求，準確的軌道占用判別能夠幫助列車確定目前所在股道及位置，從而實現列車在車站進行越行、交會或調車作業。因此高精度、可靠的軌道占用判別技術對列車運行控制系統起著至關重要的作用。

近年來隨著我國北斗衛星導航事業的快速發展，繼美國的GPS、俄羅斯的GLONASS和歐洲的ALILEO之后我國也成為擁有衛星導航定位系統的國家。如今隨著北斗系統的加入，全球導航衛星系統GNSS(Globe Navigation Satellites System)已經應用到各種領域，尤其是鐵路領域，這對列車的傳統發展產生了巨大的影響。由于衛星定位存在信號盲區以及偏差，為實現采用GNSS進行軌道占用判別，可以通過聯鎖信息輔助的方法，其中GE的增強型列控系統和ALSTOM的ATLAS-400都是通過道岔的定位、反位以及列車當前進路狀態進行軌道的占用判別[2-3]。另外，可通過加速度計和陀螺儀對列車的動力學狀態測量來輔助GNSS實現對區間列車的軌道占用判別[4]。但以上方法仍依賴一定的軌旁設備，增加了運營和維護成本，采用陀螺儀在高緯度地區無法保證航向精度，低緯度情況下無法正常轉入導航，數據不能滿足航向修正需求[5]。考慮以上方面，本文提出基于GNSS雙差定姿的區間列車軌道占用判別方法。通過雙GNSS接收機完成列車的二維姿態測量，為保證測量信息的精度和完好性，提出基于粒子濾波的風險敏感濾波算法，通過引入風險敏感因子解決由于系統的不確定性而導致濾波器魯棒性差以及發散問題。股道占用判別采用支持向量機分類法通過軌道數據庫按照數據位置相似程度組成類別，然后將具體數據正確歸入某一軌道數據組，最后驗證了方法的可行性。

1 基于GNSS雙差定姿的區間列車軌道占用判別系統

基于GNSS雙差定姿的列車軌道占用判別系統分為信息采集、定位姿態信息處理、軌道占用判別3部分部分，見圖1。

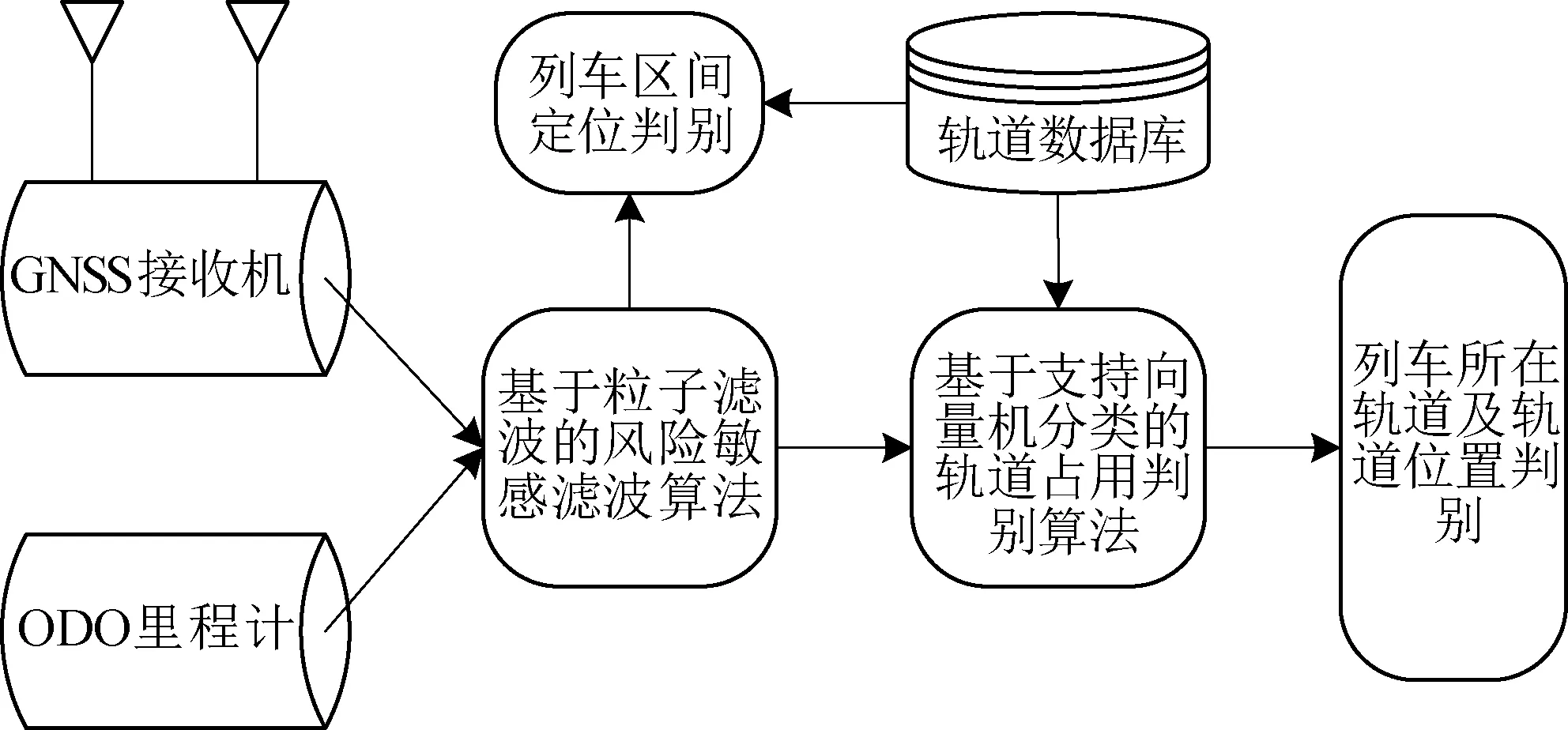
圖1 系統結構示意圖

其中信息采集部分包括GNSS接收機采集的經緯度、速度、時間和車載ODO里程計的速度信息。定位姿態信息處理部分主要采用算法完成信息的預處理，以及列車區間定位判別。軌道占用判別部分主要通過算法及軌道數據庫完成列車所在軌道及位置的判別。

2 列車GNSS雙差定姿數學模型

2.1 GNSS雙差定姿原理

GNSS雙差定姿原理是在運動載體上相距一定的距離分別安裝兩個衛星信號接收天線。此時，兩個天線便能夠同時測量多顆衛星的載波相位，通過求差解得天線之間的基線向量，從而獲得運動載體的姿態參數[5]。雙差定姿原理是由傳統單差變換得到，雙差示意見圖2。

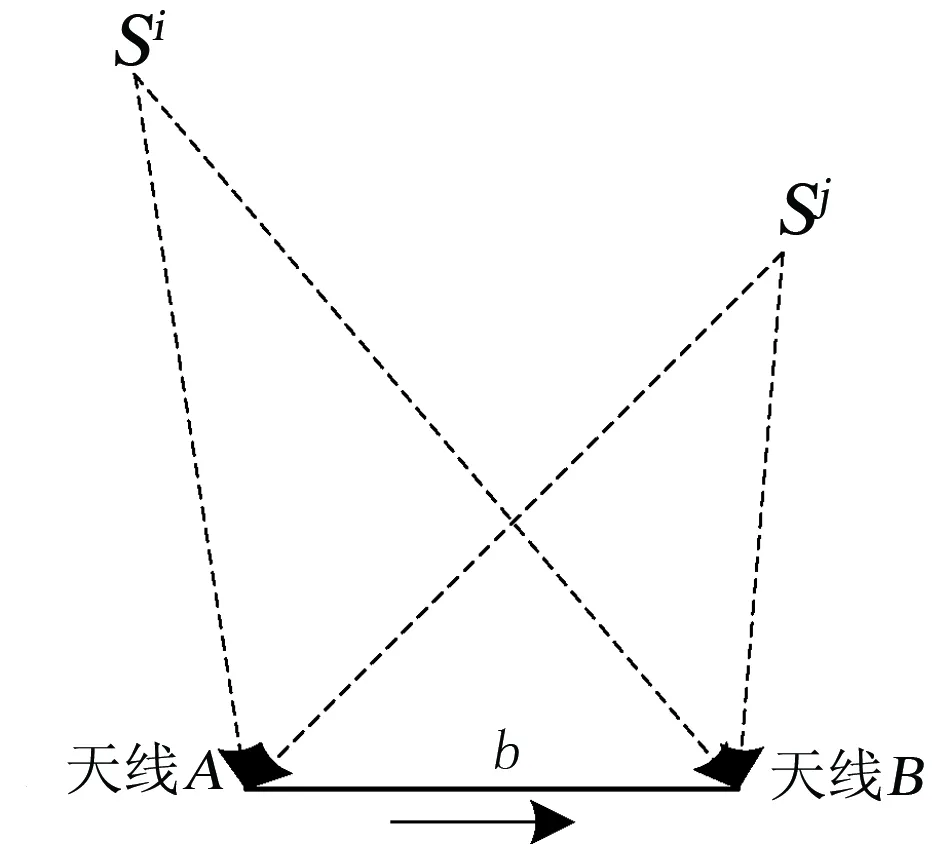
圖2 雙差示意圖

由于AB為載體上兩個GNSS天線之間的距離，因此其長度遠小于觀測衛星與載體之間的距離，此時，把衛星信號可看作平面波。假設A和B兩個衛星天線同時觀測到衛星i和j，則雙差相位基線AB的雙差載波相位觀測方程為

(1)

令

(2)

可得

(3)

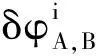
令S=Sj,i，根據式(3)得到天線A到天線B的基線向量最小二乘估計為

(4)

采用MLAMBDA方法對整周模糊度進行求解。計算結果采用大地坐標系WGS-84。為方便后續計算，將WGS-84坐標系轉換成當地水平坐標系LLS(Local Level System)。此時，運動載體的姿態角就轉換為載體坐標系BFS(Body Frame System)相對于當地水平坐標系的位置。

(5)

因此，運動載體的航向角為

(6)

2.2 列車GNSS雙差定姿模型

本文將GNSS雙差定姿理論引入區間列車軌道占用判別中，通過安裝在列車上的兩個GNSS天線獲取定位信息，通過雙差計算得到列車航向角，見圖3。其中AB為列車定位基線，其長度為列車車頭的長度，因為基線越長其航向角誤差越小，對于列車其最長基線即為機車長度[6]。列車的運動可以看作平面中的二維運動，因此只需要確定其航向角即可。

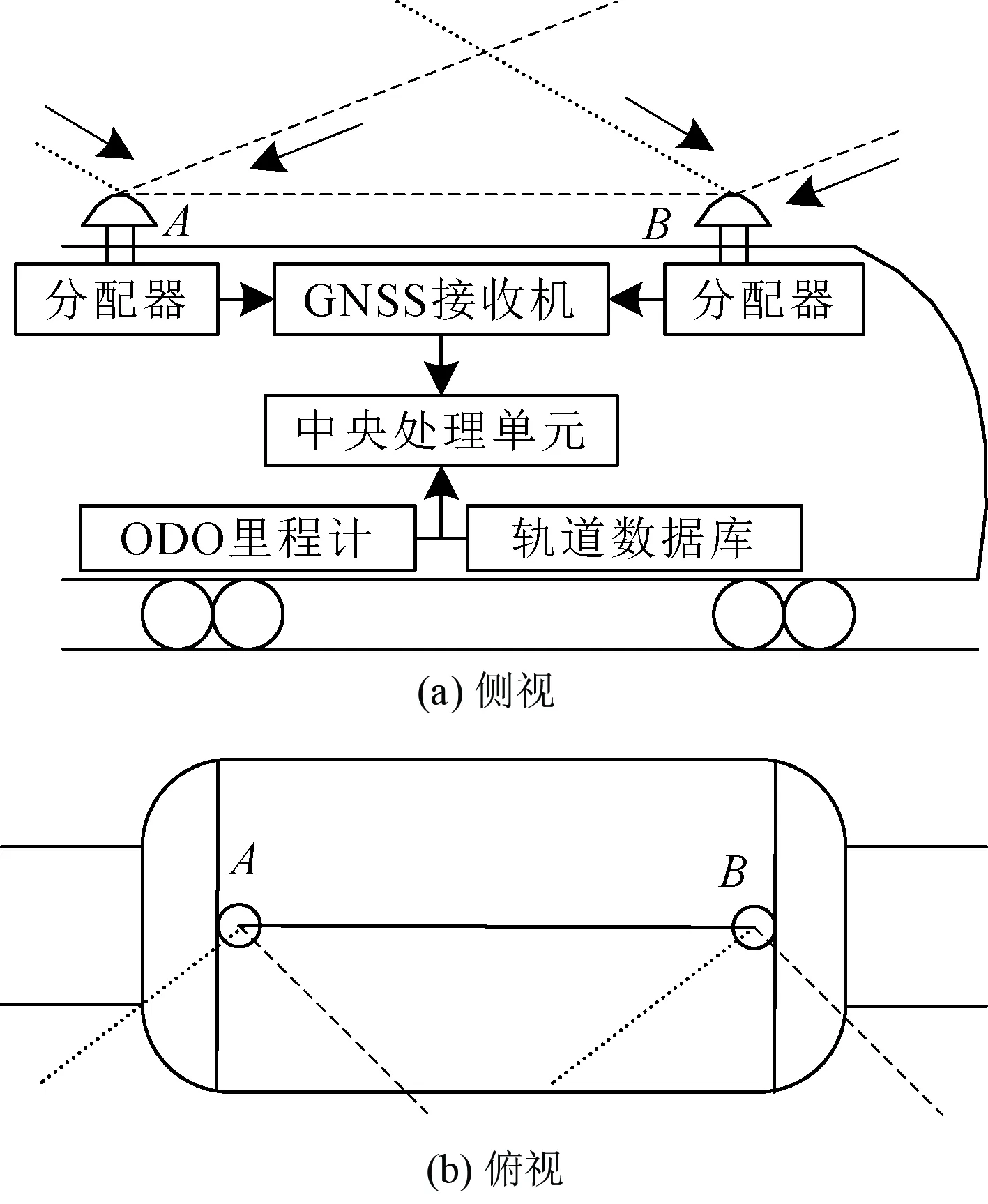
圖3 列車GNSS雙差定位示意

3 列車軌道占用判別方法

3.1 姿態信息處理算法

雖然通過雙差定姿能夠獲取列車航向角信息，但由于GNSS定位存在一定的誤差，因此需要對數據進一步處理。其中文獻[7]將GNSS接收機GG-24設置在RTK方式下，采集了列車經過道岔時的航向角信息，數據誤差的變化曲線見圖4。

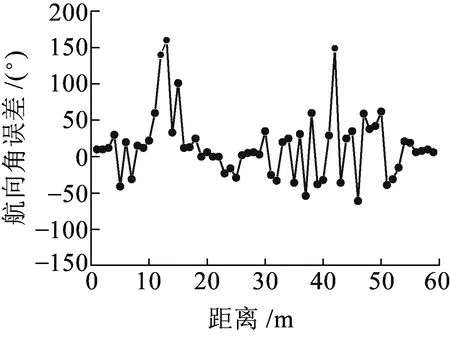
圖4 列車經過道岔的航向角誤差

由圖4可見，衛星定位系統輸出的航向角信息在慢速時存在較大偏差(列車經過道岔時會降低速度)，因此對于判斷列車的方向也會受到一定影響[7]。針對以上問題,本文提出基于粒子濾波的風險敏感濾波算法，設狀態空間模型為

(7)

式中：xn為n時刻m維線性狀態列向量；yn為n時刻的觀測值；h(xn)為關于xn的任意非線性函數；A為已知狀態的轉移矩陣；un、vn為均值為零的高斯分布狀態噪聲和觀測噪聲[8]。

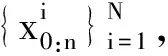
(8)

式中：i=1,…,N。

首先采樣得到粒子，即在先驗概率分布p(x0)上做采樣處理。隨后通過概率分布

(9)

得到粒子更新，其中狀態噪聲服從高斯分布，由式(8)得到粒子重要性權重為

(10)

經過歸一化后

(11)

經過重采樣后，得到狀態xn的最小均方估計為

(12)

當粒子濾波受觀測噪聲較大影響時，不能準確描述后驗概率，粒子濾波的估計性能會受到嚴重影響。

由于對狀態xn的順序估計滿足

(13)

(14)

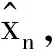
frs,n(xn)=

(15)

式中：μ1≥0,μ2≥0為風險敏感參數；函數ρ1(·)和ρ2(·)為嚴格凸的連續函數[9]。

最小風險敏感估計為

(16)

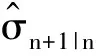
(17)

式中：X、Y為隨機變量是概率論中特有的變量；x、y為函數自變量。根據以上假設有

σn|n-1(xn)dxn

(18)

(19)

3.2 軌道占用判別算法

支持向量機SVM(Support Vector Machine)是Vapnik[10-11]根據統計學習理論提出的用于解決小樣本模式識別問題的方法。支持向量機分類器構造的基本思路是：尋求一個超平面(決策函數)，以決策平面為基準獲得最大的正負類樣本點間隔，在線性可分和不可分的情況下，轉換為二次規劃問題，最后采用拉格朗日乘子法求得唯一的極值點。

本文通過列車經過不同道岔時航向角的變化將采集到的信息進行分類，求出道岔之間航向角信息的超平面(決策函數)，然后通過軌道數據庫中道岔角度信息進行匹配，以得到列車所在軌道的占用情況。列車經過道岔時的角度變化情況見圖5。

由圖5可見，列車在經過道岔時航向角為線性變化，因此支持向量機采用線性分類法。獲取列車航向角樣本集為

{(xi,yi),i=1,2,K,l}xi∈Rdyi∈R

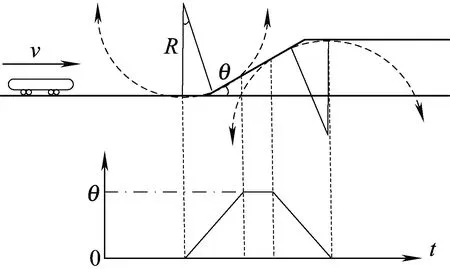
圖5 列車以恒定速度進入道岔時的角度變化曲線

他們是從某一確定函數(未知概率分布)F(x,y)中隨機獨立抽取的。同時為了使樣本能夠獲得正確的分類，還需滿足一定的約束條件

yi(w·xi+b)-1≥0

(20)

式中：b為誤差偏值；xi為樣本輸入值；w為可調權值函數。

線性最優分類圖見圖6，其中H為分類線；H1、H2分別表示離分類線最近的各類樣本，其滿足條件：H1和H2均平行于分類線H, 他們之間的距離為分類間隔。

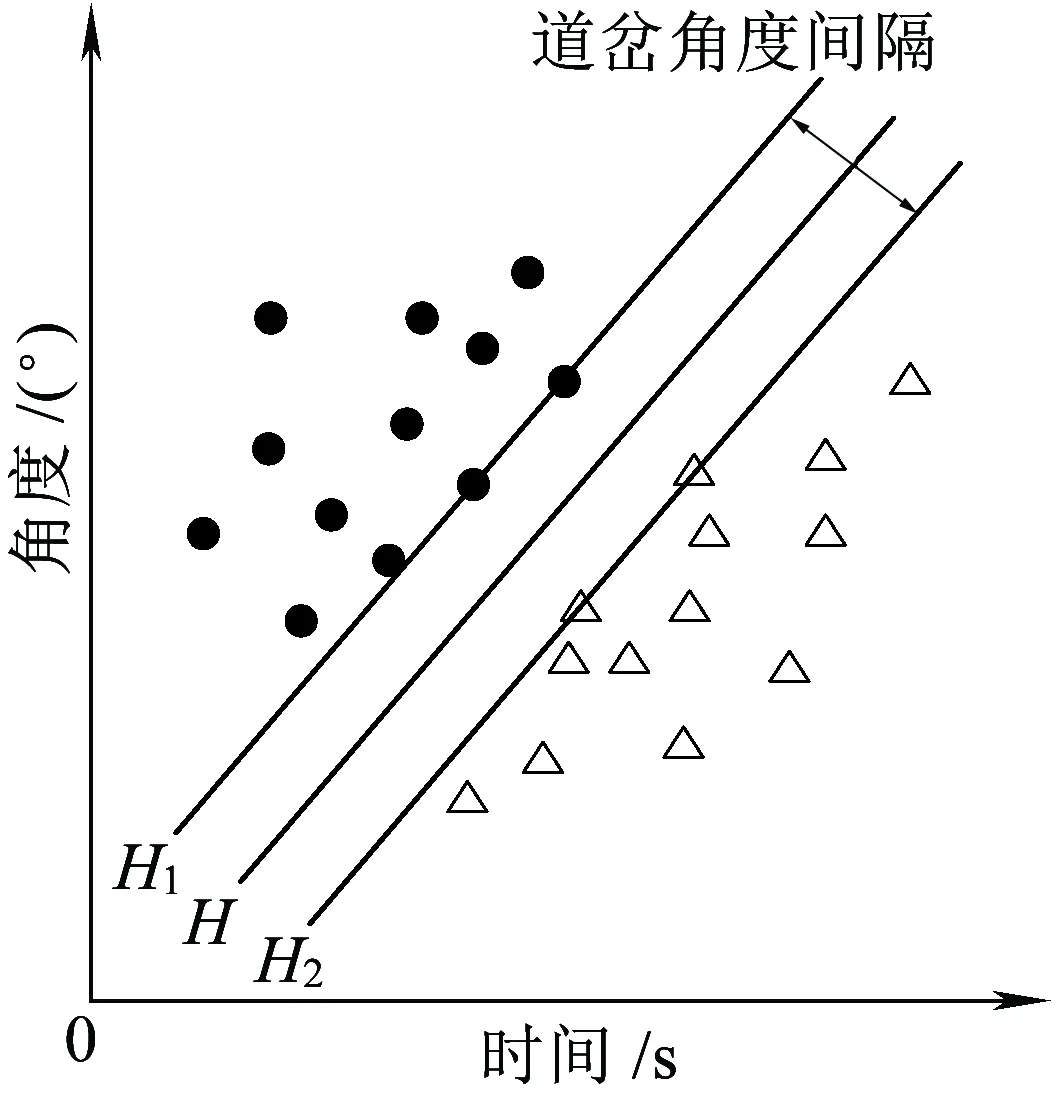
圖6 線性最優分類

在線性可分的條件下，得出分類間隔為

(21)

把求解最優超平面表示成如下約束問題,在約束條件(20)下，最小化函數為[12]

(22)

采用拉格朗日乘子法解算最優化問題。建立拉格朗日函數為

L(w,b,α)=

(23)

式中：變量αi為拉格朗日乘子且滿足條件αi≥0。拉格朗日函數L(w,b,α)的鞍點決定了約束最優化問題的解，通過對w和b求偏導并置結果等于零，通過以下兩個條件

(24)

將上述問題轉換為一個“對偶”問題。即

(25)

這是一個不等式約束二次函數極值問題，根據KKT(Karush-Kuhn-Tucker)條件，該問題滿足[13]

αi{[(w·xi)+b]yi-1}=0

(26)

可見對于大多樣本αi值為0，其中不為0的αi對應使式(20)中等號成立的樣本，即支持向量。求解上述問題后得到的最優分類函數為

(27)

通過以上分析，區間軌道占用判別流程見圖7。

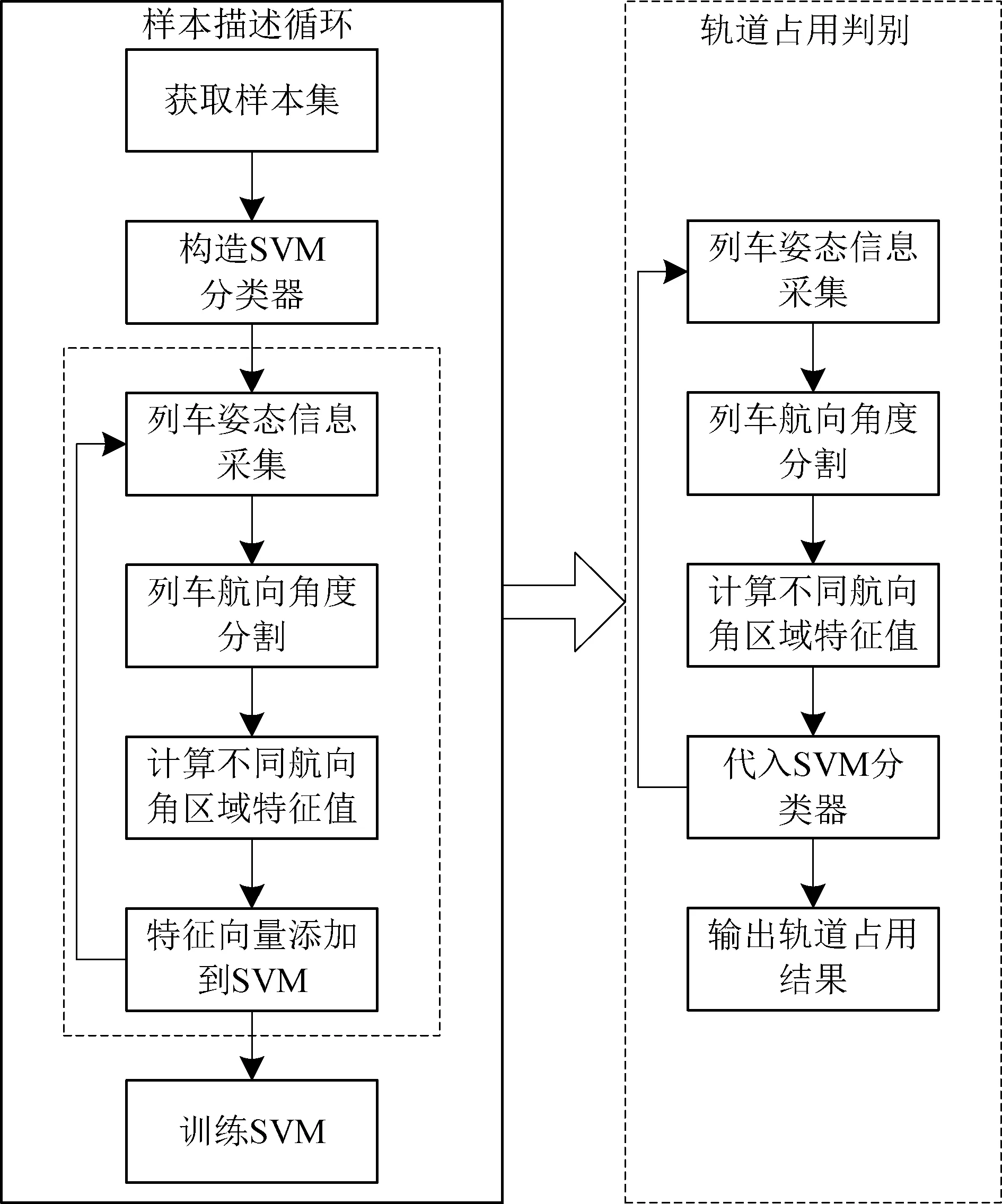
圖7 基于SVM分類的軌道占用判別流程

4 算法驗證與分析

結合長沙磁懸浮列車現場測試數據進行分析，利用里程計、慣性測量單元、GNSS接收機所采集到的數據進行MATLAB處理，驗證本文提出的基于粒子濾波的敏感風險因子濾波算法的優越性以及軌道占用判別方法的有效性。

4.1 測試參數及環境

測試硬件部分主要采用K700衛星定位板卡。K700為3系統單頻OEM板卡，支持BDS B1、GPS L1、GLONASS L1 共3個系統，支持SBAS系統，輸出頻率為10 Hz。慣性測量單元采用6軸的MUPU6050，采樣頻率100 kHz，啟動時間400 ms。硬件設備現場測試見圖8(a)。測試路線為長沙磁懸浮線路，磁懸浮高鐵站到磁懸浮機場站線路全長18.55 km，見圖8(b)。本文選取部分測試數據進行處理分析。

(a) 硬件設備測試

(b) 測試路線圖圖8 現場測試

4.2 GNSS雙差定姿濾波算法驗證

選取部分測試數據進行處理，測試路段的可見衛星數分布見圖9。

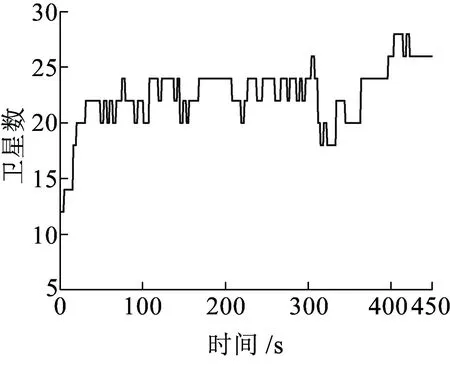
圖9 測試路線衛星數分布圖

通過MATLAB對安裝在機車前后的GNSS衛星接收機采集到的原始數據進行雙差計算，得到列車運行的航向角變化曲線見圖10。同時采用本文提出的基于粒子濾波的風險敏感濾波算法對雙差結果進行濾波處理，濾波前后的航向角變化值見圖11。可見在經過道岔時GNSS雙差計算存在較大波動，而本文提出的濾波算法對解決非線性定姿系統存在較大初始誤差的濾波問題取得了較好的效果。

為進一步說明該算法的優越性，通過與基站的絕對坐標對比獲得數據的誤差分布,采樣的頻率次數與誤差分布的直方圖，見圖12(a)。其誤差達到±7 m，其中兩端誤差為±7 m的范圍存在次數較多，發散性強且魯棒性差。

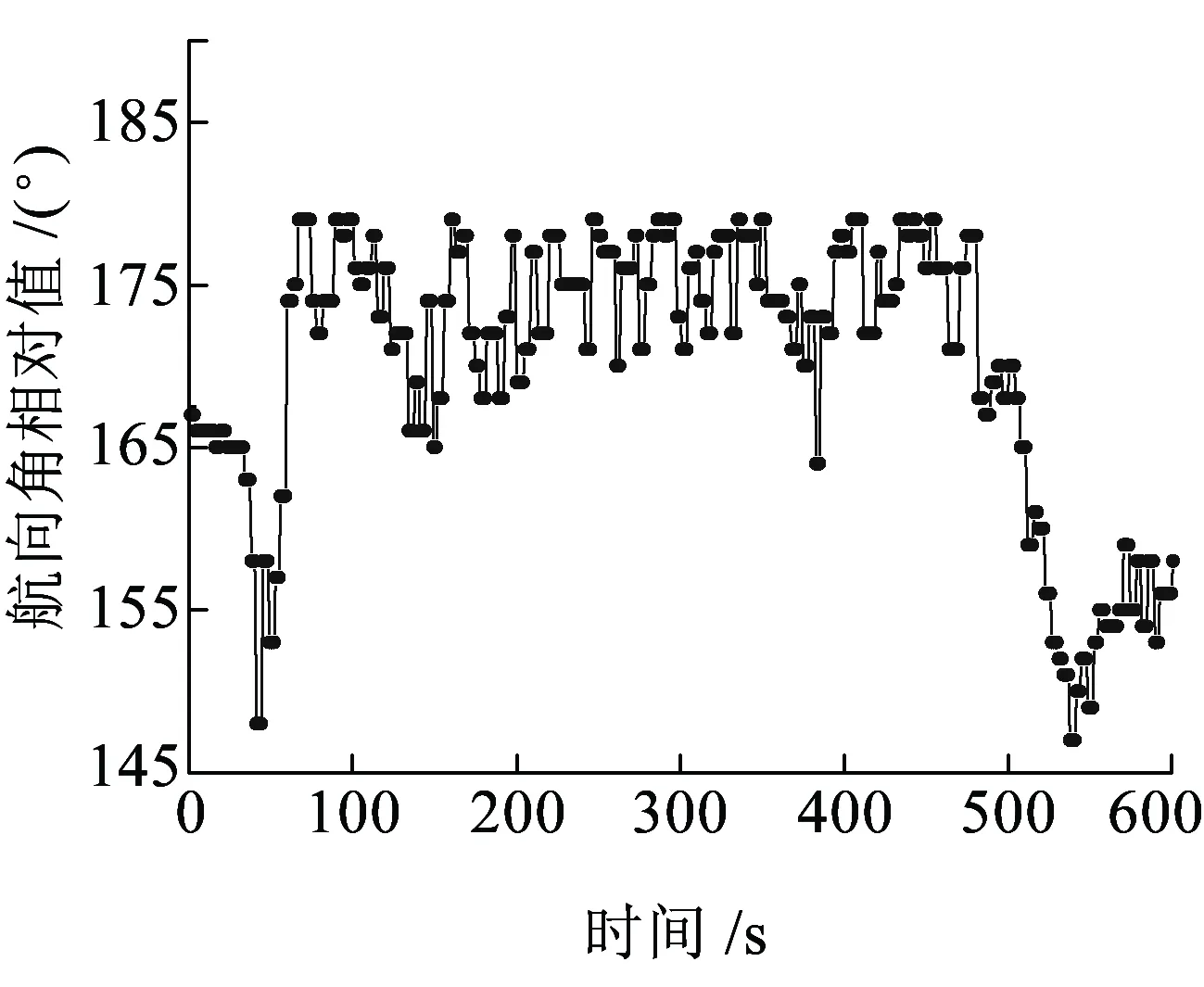
圖10 列車GNSS雙差測量航向角

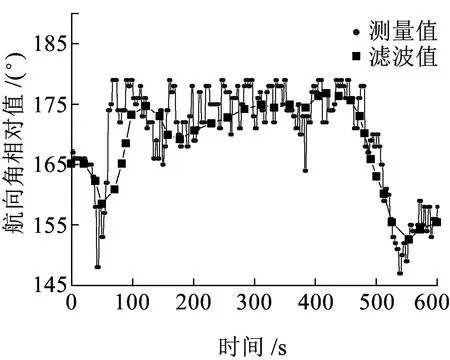
圖11 濾波結果與原始測量值比較

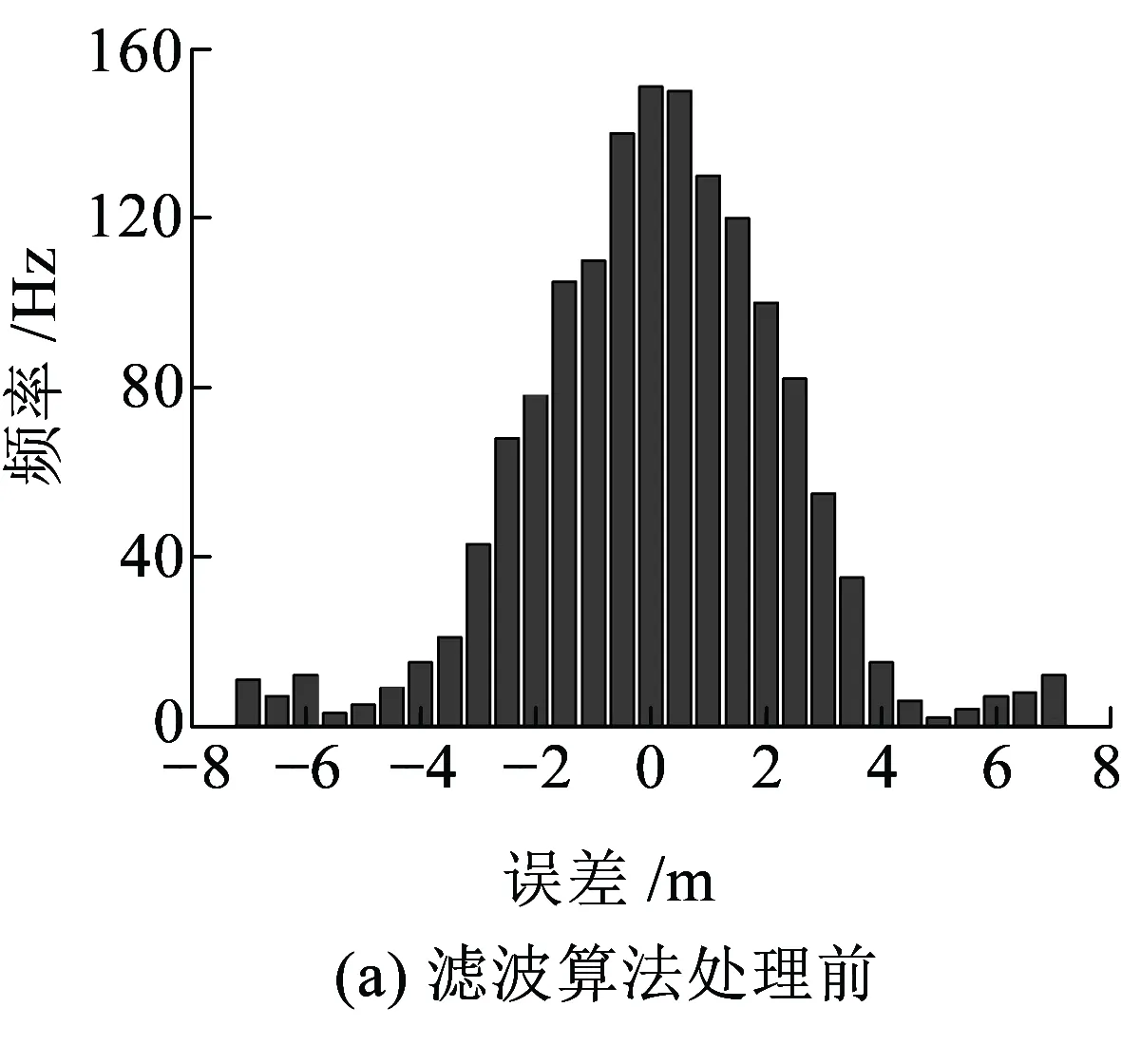
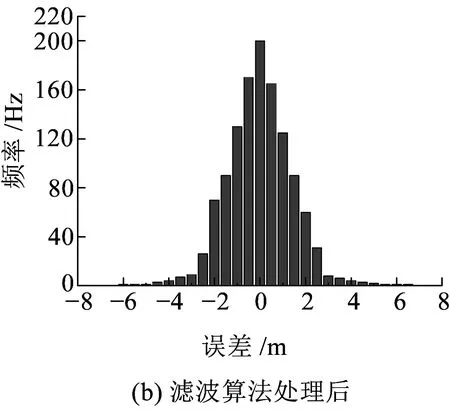
圖12 濾波算法處理前后的GNSS定位誤差分布

經過基于粒子濾波的風險敏感濾波算法處理后的GNSS定位數據誤差分布，見圖12(b)。一般鐵路區間平行股道中心距離為5 m，列車GNSS定位橫向誤差滿足零均值的高斯白噪聲。0.999 99的置信度要求轉換為定位精度為4.3倍標準差(4.3σ),則定位精度即為[14-15]

4.3σ=4.3×0.58=2.494

(28)

根據圖12中的數據可知，在精度為2.494 m范圍內的概率分別為93.23%和99.5%，在支持向量機分類輔助下能夠滿足平行股道占用判別。

4.2 列車軌道占用判別仿真分析

通過MATLAB編寫相關分類算法程序。為說明實驗結果，此處定義軌道占用判決正確率為

(29)

式中：N為誤判類別總數；T為每種誤判類別的樣本數；S為正確判決的樣本總數。

4種狀態下的判決分類結果，見表1。

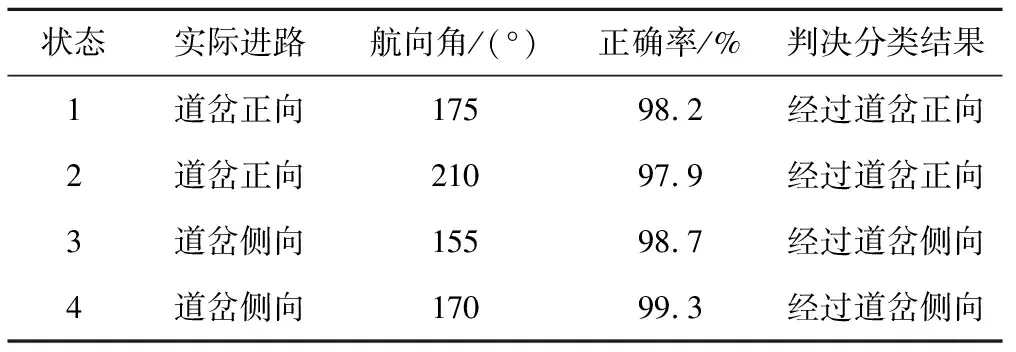
表1 列車軌道占用判決分類結果

4.3 衛星數及HDOP值對軌道占用識別的影響

可見衛星數及水平(平面)位置精度因子HDOP值對基于GNSS雙差定姿的列車軌道占用判別具有重要的影響，為提高軌道占用判別的完好性和可靠性，必須對數據的有效性進行分析。研究表明，當可用衛星數在6顆以上、HDOP值低于1.5時才能滿足軌道占用判別要求[16]。通過現場采集提取相關數據繪制成,見圖13。

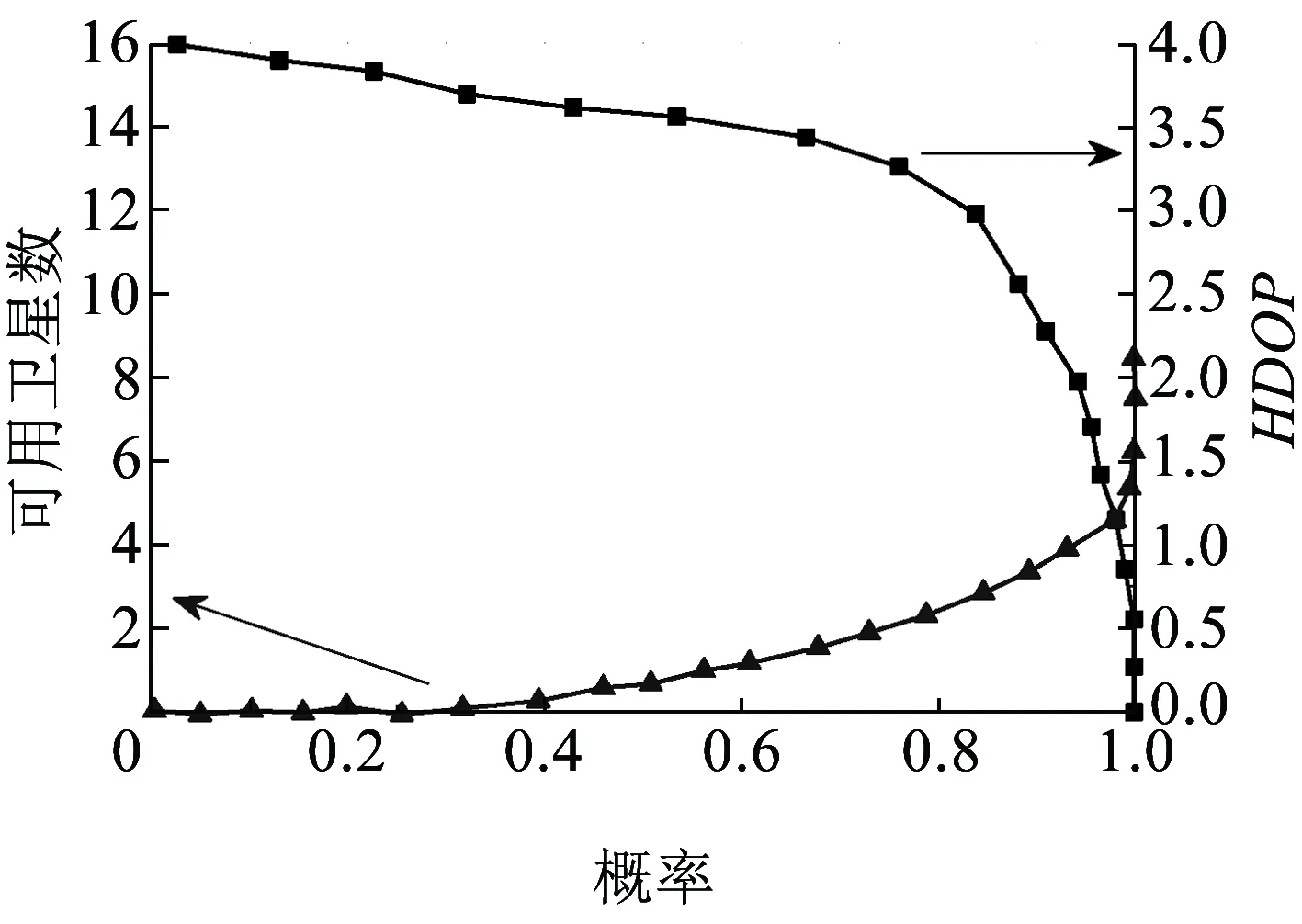
圖13 衛星數及HDOP值與軌道占用概率的關系

由圖13可以看出，當可用衛星數在5顆及以上時、當HDOP低于2.0時其軌道占用判別概率能夠達到95%以上，從而優于傳統測試參數，為未來衛星導航定位技術在列車中的應用提供一定的參考價值。

5 結束語

針對區間列車軌道占用判別問題，提出基于GNSS雙差定姿的軌道占用判別方法。通過引入風險敏感因子，提出一種基于粒子濾波的風險敏感濾波算法，有效地解決了由于系統的不確定性而導致濾波器魯棒性差以及發散的問題。對于軌道判別方面，采用一種支持向量機的分類算法。經過數據分析與仿真，該方法能夠基本完成列車軌道占用判別，下一步的工作是對該方法進行完善。