基于神經網絡的金融市場艾略特波浪識別

李音潤 歐 鷗

(成都理工大學信息科學與技術學院 四川 成都 610059)

0 引 言

隨著機器學習、人工神經網絡、強化學習和深度學習等人工智能技術的發展，人工智能技術被成功應用于圖像處理、語音識別和自然語言處理等領域。人工神經網絡屬于機器學習領域的一個分支，具有非線性、自適應的分布式并行結構，可用于解決分類和回歸問題。

金融市場結構復雜、波動頻繁的特點受人類社會經濟和自然各方面因素影響。大量復雜的變化因素導致研究分析市場行為的困難增加。艾略特波浪理論被成功應用于金融市場的分析。該理論由R.N.艾略特[1](Ralph Nelson Elliott)提出。艾略特認為金融市場的波動行為遵循一定的模式，僅在范圍和時間上有區別，他將這類模式定義為“艾略特波浪”。此外，波浪理論不僅適用于描述交易市場的變化行為，還可正確描述人類群體性行為以及各種自然現象，因此又稱之為“自然法則”。

盡管艾略特波浪理論具有較高的準確性，但目前國內學者對它的研究較少，將人工智能應用于該理論的研究更是寥寥無幾。鑒于這種現狀，本文提出利用人工神經網絡技術，從金融市場的歷史數據中識別、提取出艾略特波浪模式。本文介紹了兩種基于人工神經網絡的技術——傳統的后向傳播神經網絡和模糊神經網絡，并根據這兩種技術設計出識別艾略特波浪模式的分類器。傳統后向傳播網絡在研究和實驗過程中表現了一些缺陷，于是在傳統后向傳播網絡的基礎上引入了模糊神經網絡。本文引入的模糊神經網絡在學習算法、網絡結構等方面對傳統后向傳播網絡進行改進，并通過實驗驗證和比較了兩種分類器的識別效果。

1 相關研究

文獻[2]最早提出了分析和預測金融市場變化的模型——ARIMA模型，該模型采用時間序列表示金融市場的歷史交易數據，包括自回歸、差分和平均移動三個部分。ARIMA模型的提出奠定了金融市場模型研究的基礎。此后，涌現了大量基于時間序列的預測模型，Gooijer等[3]對這些模型做過系統性總結和比較。

金融市場預測模型的技術熱點主要在機器學習領域，包括人工神經網絡、支持向量機、貝葉斯方法、決策樹等，以及在此基礎上，多種方法相結合的混合技術。市場的預測對象主要有價格預測和趨勢預測。相比之下，趨勢預測的可行性和實用性更高。

近年來，利用人工神經網絡技術建立金融市場預測模型的研究熱度很高。技術包括多層感知機(MLP)、動態人工神經網絡(DAN2)和混合神經網絡[4]。概率神經網絡(PNN)在預測股票指數的未來變化方向上表現良好[5]。此外，Manahov等[6]使用基于強類型遺傳規劃(STGP)的算法對富時100指數、標準普爾500指數及羅素3 000指數進行分析，發現了股票市場的動態和非線性結構。

除人工神經網絡的方法外，支持向量機[7]、模糊系統[8]和基于多種理論的混合模型[9]，經過實驗證明，也具有較高的可靠性。

隨著深度神經網絡技術[10]的發展，文獻[11]提出了一種基于深度學習的高頻策略，并用實驗證明，該策略的定向精度高達66%。Chong等[12]比較和總結了1980年至今提出的各種股票市場預測模型，并將深度學習系統地運用在股票市場的分析和預測上。

根據時間的變化范圍，可將股票市場的預測分為兩類——長期和短期。長期預測通常指在周、月、季及年的時間范圍內進行價格或趨勢預測，短期預測指對分鐘、小時及當日交易的預測。多數研究者更關注短期預測[11-13]，即高頻交易。

根據Prechter[14]對艾略特波浪理論和股票市場波動的描述，我們可以得出結論，艾略特波浪比純粹的股票價格信息更能反應金融市場的本質，正確識別艾略特波浪模式即可正確判定未來市場走勢。使用艾略特波浪理論可實現對金融市場價格和趨勢的全面預測，該理論對長期和短期的市場變化均適用。不同于上述這些利用股價數據直接分析預測金融市場的技術，本文關注于艾略特波浪模式的識別。

2 后向傳播神經網絡

2.1 傳統的后向傳播神經網絡

后向傳播神經網絡是采用后向傳播算法作為學習算法的一種人工神經網絡。神經網絡具有并行的分布式層次結構，每層由多個非線性運算單元(即神經元)構成。神經元對輸入信息進行加權，結合偏移量(或稱“閾值”)，通過非線性函數產生對應的輸出結果。底層的輸出結果作為高層的輸入數據，進而實現從大量輸入數據中發現分布式特征的目的。神經元使用的非線性函數被稱作激活函數，sigmoid函數是其中最常用的一種。對第i個神經元使用sigmoid函數進行運算處理由公式表示：

(1)

式中：xj表示輸入神經元i的第j個數據，wij表示由上一層神經元j至本層神經元i的連接權重值，bi表示神經元i的偏移量。

后向傳播神經網絡通過前向傳播得到輸出結果，通過后向傳播修正權重和偏移量等網絡參數。式(1)實現了從輸入到輸出的前向傳播過程。設第i個神經元的預期輸出結果為di，單個輸入樣本k的總體誤差函數由公式定義：

(2)

輸出層的權重修正公式：

(3)

式中：δi是輸出層單元i的誤差項，δi=outi(1-outi)·(di-outi)。

同理可得偏移量的修正公式：

(4)

以三層神經網絡為例，hj表示隱藏層的輸出值，那么隱藏層的第j個神經元的誤差項由公式表示：

(5)

學習率η越高收斂速度越快，但會導致振蕩現象。引入動量因子α可削弱振蕩現象則有：

Δwij(n)=ηδixj+αΔwij(n-1)

(6)

n表示當前的迭代次數。隱藏層的權重值、偏移量的修正公式與式(3)、式(4)類似。迭代進行上述操作。

2.2 傳統后向傳播神經網絡的問題

后向傳播神經網絡存在以下三個問題[15]：

? 后向傳播算法可能得到局部最優結果，即不能保證收斂結果是全局最優[15]；

? 對隱藏層神經元的分析通常比較困難；

? 算法的收斂速度較慢，收斂速度受權重的影響較大。

為改進傳統后向傳播神經網絡，提高收斂速度并保證網絡的穩定性，本文在傳統后向傳播算法的基礎上引入了縮放共軛梯度算法SCG(Scaled Conjugate Gradient)。

另外，在金融市場的實際交易中，當前價格所處的艾略特波浪有多種可能且發生概率相同，這便引入了分類邊界模糊的問題。模糊理論是解決這類問題的有效方法。

考慮到以上兩大問題，本文將縮放共軛梯度算法和模糊理論引入傳統后向傳播神經網絡，提出第二種基于人工神經網絡的艾略特波浪模式分類器。這便是下面介紹的基于SCG算法的模糊神經網絡。

3 模糊神經網絡

3.1 模糊理論

模糊神經網絡是結合了模糊理論的人工神經網絡。模糊算法是基于if-then規則的分類器，該算法遵循模糊理論的規則。模糊理論由Zadeh[17]提出，是關于模糊集和隸屬函數(membership function)的分析方法。模糊集通過隸屬函數實現邊界定義模糊的分類，即某個數據可以同時隸屬于多個類。使用模糊神經網絡，元素(即數據)的分類結果由隸屬度表示。論域中每個元素對模糊集的隸屬度由隸屬函數計算得到。已知論域U，函數μM(·)可將論域U映射至[0,1]，論域U上的模糊集M由下式定義：

M={〈μ,μM(u)〉|u∈U}

(7)

式中：函數μM(·)是模糊集M的隸屬函數，論域的元素u∈U進行隸屬函數μM(·)映射后得到的值被稱為元素u對模糊集M的隸屬度。

常見的隸屬函數有以下四種：

? 三角形隸屬函數：

? 高斯隸屬函數：

? 鐘形隸屬函數：

?sigmoid隸屬函數：

其中，{a,b,c,d,δ}為上述隸屬函數的參數。

圖1展示了一個基本的模糊系統。

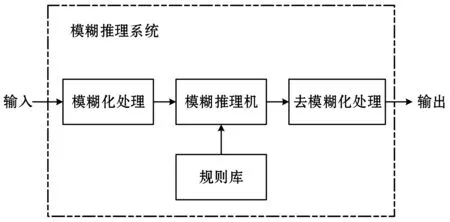
圖1 簡單的模糊系統

根據模糊規則的不同，可將模糊系統分成多類，其中應用最廣的是Mamdani模糊系統、Sugeno模糊系統和Tsukamoto模糊系統。

以Sugeno模型為例，對于有兩個輸入(x,y)和單輸出z的一階Sugeno模型，其if-then規則集有：

? 規則1：ifx是A1andy是B1，thenz=f1(x,y)=p1x+q1y+r1；

? 規則2：ifx是A2andy是B2，thenz=f2(x,y)=p2x+q2y+r2；

3.2 基于SCG算法的模糊神經網絡

為了將模糊理論與神經網絡相結合，張智星等[18]提出了神經-模糊系統(簡稱ANFIS)。該系統有五層網絡結構。以Sugeno模糊系統為例，設有兩個輸入(x,y)，ANFIS的結構如圖2所示。

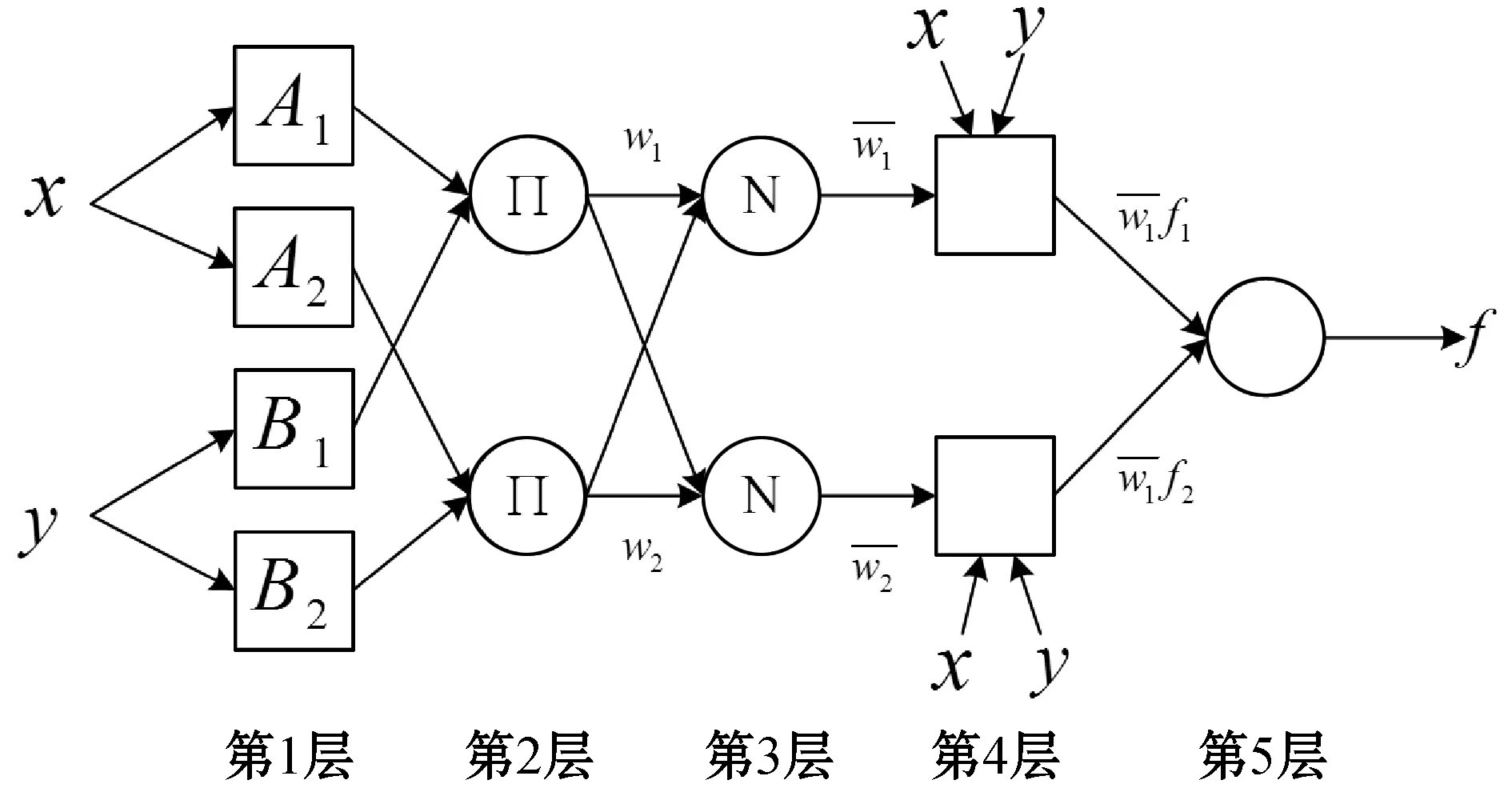
圖2 具有兩個輸入的ANFIS結構[18]

網絡的第1層計算輸入對模糊集的隸屬度，實現模糊化處理；第2層計算規則1和規則2的激勵強度；第3層計算每條規則的激勵強度與所有規則的激勵強度的比值，實現激勵強度的歸一化；第4層根據Sugeno模糊規則設定三個參數{pj,qj,rj}，該層由具有激活函數的自適應單元組成；第5層計算總輸出。用Oi,j表示第i層的第j個單元的輸出值，各層操作如下所示：

? 第1層：O1,j=μA,j(x)j=1,2

O1,j=μB,j-2(y)j=3,4

? 第2層：

O2,j=wj=μA,j(x)μB,j(y)j=1,2

? 第4層：

? 第5層：

ANFIS網絡需要訓練和修正兩類參數——前提參數和結論參數，即隸屬函數中的參數和根據模糊規則設定的參數。文獻[18]認為，當前提參數取固定值后，最終的輸出可由結論參數的線性組合表示，如公式所示：

(8)

ANFIS網絡由前向傳播和后向傳播組成。前向傳播的輸出值由式(8)得到。后向傳播迭代修正權重值的基本公式如下：

wk+1=wk+ηkPk

(9)

(10)

CG算法在迭代過程中通過線性搜索確定步長，會消耗大量時間。為解決該問題，文獻[19]提出了縮放共軛梯度法(SCG算法)。該算法引入尺度因子λk，用Hk+λkI代替單純的Hessian矩陣Hk。SCG算法的步長公式為：

(11)

基于SCG算法的神經網絡大大加快了收斂速度，同時保證了網絡的穩定性。從理論上講，該網絡的實用效果，應該優于傳統后向傳播網絡。

4 艾略特波浪理論

艾略特波浪理論的基本思想源于分形理論和斐波那契數列。R.N.艾略特通過對道瓊斯工業平均指數的研究，發現金融市場的波動是有韻律的循環行為，他提出用波浪(即艾略特波浪)來描述這種變化行為。一個完整的循環波浪由驅動浪和調整浪組成。驅動浪由五個浪組成,調整浪由三浪或其變體組成,圖3展示了調整浪為鋸齒形的循環波浪。“調整”是對部分“驅動”價格的回撤，這種部分回撤的關系滿足黃金分割率。

金融市場不斷重復圖3的波浪行為，因此只要確定市場當前價格所處的波浪位置，即可正確預測市場的未來走勢。利用神經網絡對艾略特波浪理論建模的關鍵在于正確識別并提取波浪模式。

(a) 牛市里的循環波浪

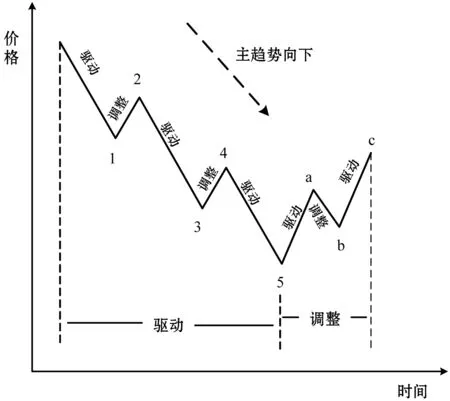
(b) 熊市里的循環波浪圖3 完整的循環波浪

根據驅動浪由五個浪組成，調整浪由三個浪組成的原則，圖3中的浪1、3、5及浪a、c可細分為5個更小級別的波浪，浪2、4及浪b也由3個更小級別的波浪組成。于是，以圖3-a的浪Ⅰ為例，浪Ⅰ可由圖4所示的結構表示。

圖4 艾略特波浪的分形結構

雖然圖4的波浪形態比圖3的復雜，但波浪的基本結構相同，即都由驅動浪和調整浪組成。從本質上講，這種特性遵循了分形理論的自相似性。“分形”由文獻[20]在研究英國海岸線時提出。艾略特在分形理論的基礎上，提出了“分形級別”的概念，分形級別由波浪規模和時間范圍決定。圖4中浪Ⅰ的分形級別就比浪1、浪2、浪3、浪4、浪5的大一級。波浪的分形級別在小時圖、日圖、周圖等不同時間范圍的K線圖中表現尤為顯著。文獻[14]中還提到，只要不終止金融市場的交易行為，波浪的分形級別就會隨時間推移而不斷增長。而且這種增長符合對數螺線的變化規律。能否正確區分波浪的分形級別是預測市場未來走勢的關鍵任務之一。

艾略特波浪具有三個不變準則[1]：

? 浪2的運動不會超過浪1的起點；

? 浪3不會是五個浪中最短的；

? 浪4不會進入浪1的價格區域。

以上三個準則適用于規則的波浪，即除不規則三角形以外的波浪。

驅動浪分為常規推動浪和傾斜三角形兩類，形式簡單，均由向上(或向下)的五個波浪組成。調整浪的形式較為復雜，以主趨勢向上的調整浪為例，可將調整浪分為圖5所示的三類。

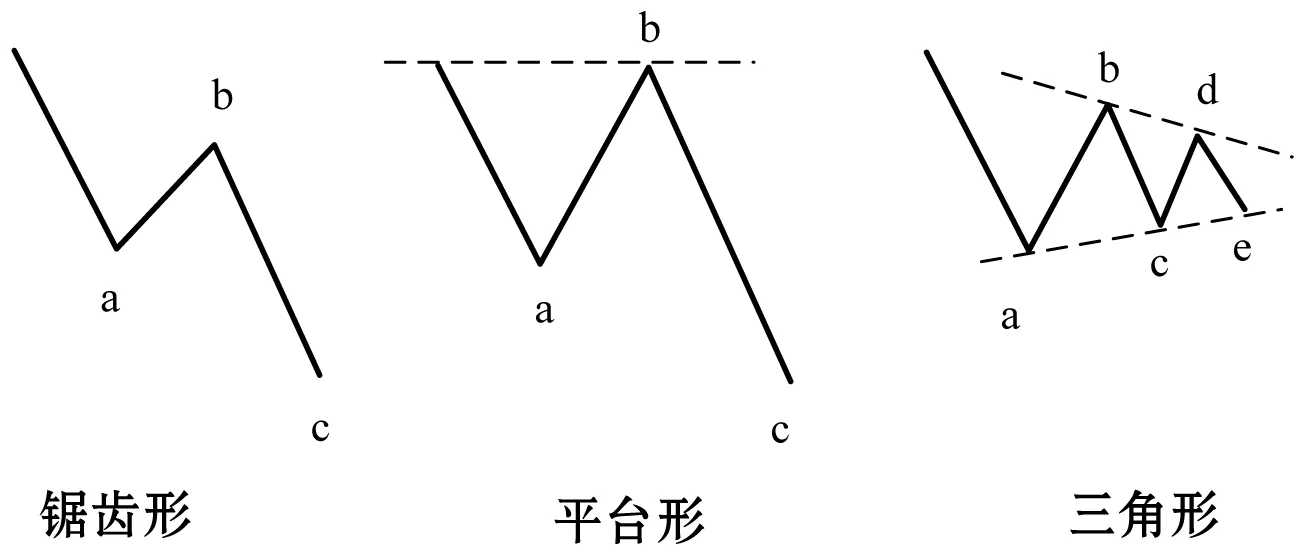
圖5 調整浪在熊市中的三種基本形式

以上三類只是調整浪的基本形式，每一類都具有相應的變體形式，例如，平臺形的調整浪又有擴散平臺形和順勢平臺形之分。由于調整浪的形式多變，在解決實際問題時，正確區分調整浪結構的難度大。

以上三類調整浪的子浪結構如表1所示。

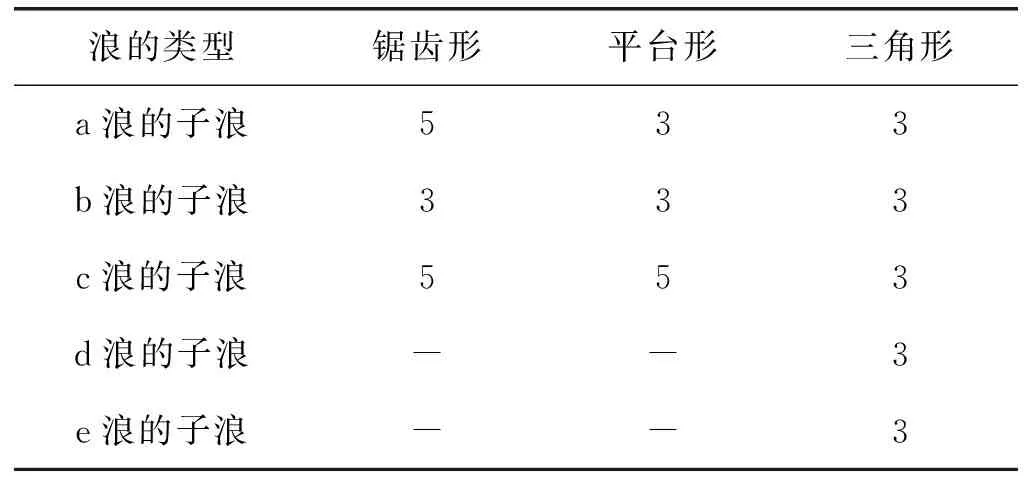
表1 三類常規調整浪的子浪結構 個

斐波那契數列是線性遞推數列：1，1，2，3，5，8，13，21，34，55，…,數列由下式定義：

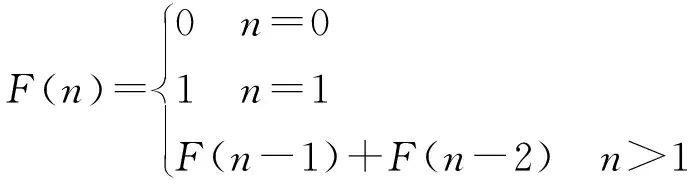
(12)

式中：前一項與后一項的比值無限趨近黃金分割比率0.618。

艾略特波浪理論在多方面體現了斐波那契數列的特點，最主要表現在波浪數和價格比例關系上。艾略特波浪的數目屬于斐波那契數列(如表2所示)，調整浪的價格的波動幅度與前一驅動浪的關系通常是0.618或0.382。

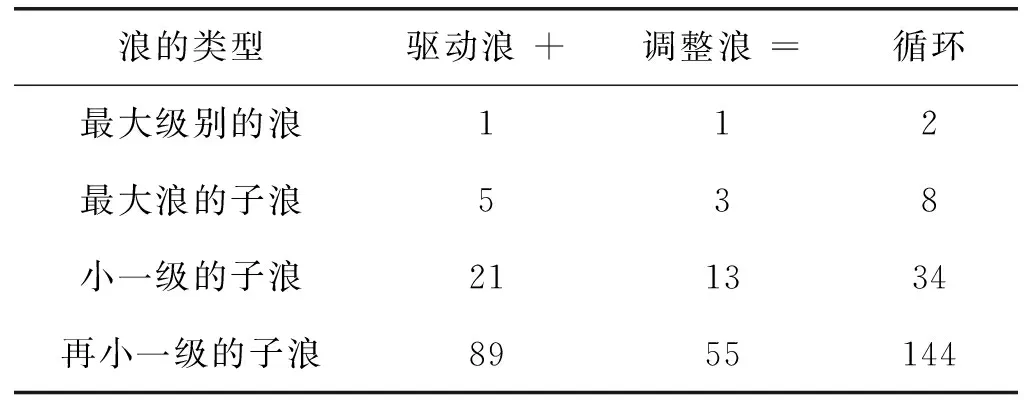
表2 波浪數和循環數 個

5 艾略特波浪模式分類器

5.1 數據處理及模式設定

艾略特波浪理論單純以股票交易日的最高價與最低價為研究對象，在股票價格指數、期貨、商品指數等穩定成熟的金融市場上表現良好。實驗采取啟發式方法，以專家知識為基礎，從道瓊斯工業平均指數、標準普爾500指數、上證指數、深證綜合指數及CRB指數中選取了以圖6為例的股價數據作為訓練集和測試集。股價的變化范圍覆蓋分鐘、小時、日、周、月和季度。

圖6 訓練集包括的14種艾略特波浪模式

首先對股價數據進行預處理。股價數據由時間序列(x1,x2,…,xn)表示，利用min-max標準化方法對時間序列作歸一化處理，將股價數據映射至[0,1]區間。訓練集和測試集由歸一化處理后的時間序列組成。min-max標準化表示為：

(13)

訓練集的選取對于神經網絡的訓練結果影響較大，選取適當的艾略特波浪是保證網絡識別效果的關鍵任務之一。依據驅動浪和調整浪兩類波浪的規則分別對波浪模式進行分類是最直觀的方法，但這種分類方法存在兩個問題：

? 調整浪的組成結構復雜、變形多，準確識別調整浪模式的難度較大；

? 調整浪和驅動浪的波浪數目一般不同，導致網絡輸入層的設置困難。

調整浪的子浪結構雖然復雜，但其整體結構總保持三浪不變。即使是三角形的調整浪，從一定程度上也可劃分為A-B-C的三浪結構。驅動浪則總是以五浪的形式展開。考慮到以上因素，實驗選擇識別的每個波浪模式均包括驅動浪和調整浪，即以完整循環浪為識別目標。通過對艾略特波浪理論和股票指數的分析、研究，實驗選取最常見的四種驅動浪和五種調整浪結合，設計了14種波浪模式(如圖6所示)。在驅動浪中，最常見的情況是第三浪和第五浪延長，因此實驗選取以下四種驅動浪：

? 第三浪延長，且第一浪和第五浪等長(模式1-3)；

? 第三浪延長，且第五浪的長度為第一浪的0.618倍(模式4-5)；

? 第五浪延長(模式6-10)；

? 三角形驅動浪(模式11、13)。

實驗選取的調整浪有以下四種：

? 鋸齒形(模式1、6和模式11-14)；

? 平臺形(模式2-5和模式7-10)；

? 衰竭形(模式3、5、8、10)；

? 三角形(模式12、14)。

實驗將上述幾種驅動浪和調整浪進行組合，得到圖6的14種波浪模式。訓練集和測試集選取的時間序列均包含圖6所示的波浪模式。

5.2 基于后向傳播神經網絡的分類器

本次實驗的目的是利用后向傳播神經網絡，從給定的金融時間序列中，分類識別出艾略特波浪模式。

實驗采用9-10-14的三層后向傳播神經網絡架構，即輸入層有9個神經元，隱藏層有10個神經元，輸出層有14個神經元。每個樣本的輸入向量包括9個元素(x1,x2,…,x9)。輸出向量包括14個元素，每個元素依次代表對應的模式類別。該網絡是全聯通的，初始權重為隨機值。為適應和修正網絡參數，設置學習率為0.2，不考慮動量因子，經過1 600次迭代訓練后的網絡的總體誤差趨于穩定，均方誤差穩定于0.86。該網絡的均方誤差變化如圖7所示。

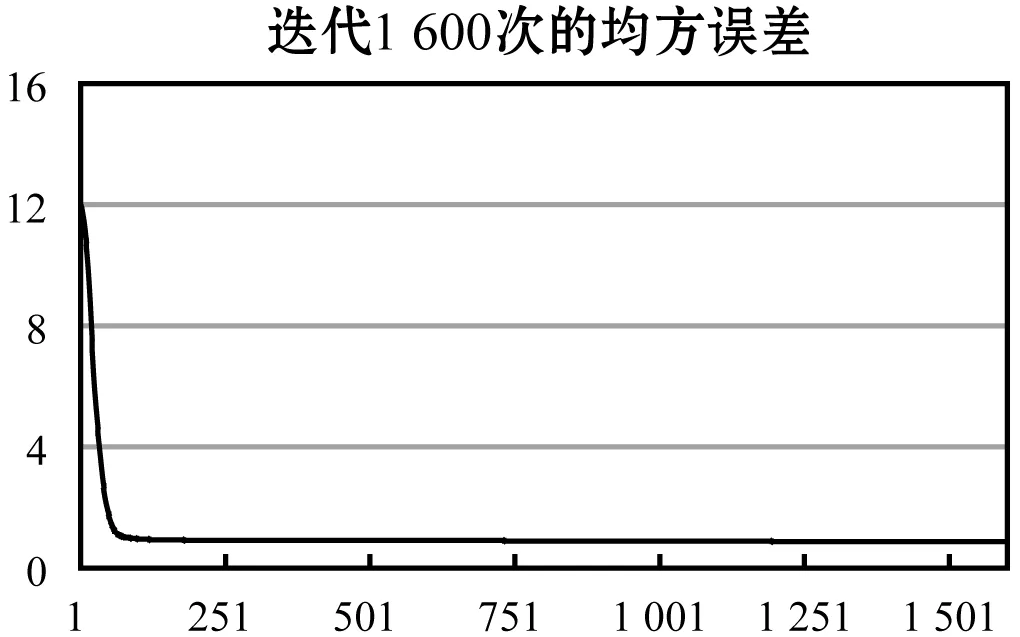
圖7 基于傳統后向傳播網絡的分類器的均方誤差

5.3 基于模糊神經網絡的分類器

為有效解決傳統后向傳播神經網絡收斂速度慢的問題，實驗選用SCG算法作為模糊神經網絡的學習算法。SCG算法的最大優勢在于它的參數(包括學習率、動量因子)是完全自動化的，不需要用戶設定。

實驗設置四層架構的模糊神經網絡，選擇高斯函數作為隸屬函數，輸入層由9個單元構成，輸出層為1個單元，輸出結果是輸入時間序列對應的波浪模式類別編號。根據輸出的波浪模式類別，實驗設定14個規則。實驗選定的訓練集和測試集與后向傳播神經網絡的相同，經過對模糊神經網絡的120次迭代訓練后，網絡的總體誤差趨于穩定，均方誤差穩定于0.21。該網絡的均方誤差變化如圖8所示。

圖8 基于模糊神經網絡的分類器的均方誤差

5.4 實驗結果的分析與比較

通過實驗證明，基于人工神經網絡的技術可以成功從給定的金融時間序列中識別分類艾略特波浪模式。我們從收斂速度和準確率兩方面比較了兩種算法的實驗結果。在評估誤差時使用了表3所示的四個評估標準。評估標準的計算公式為：

? 均方誤差：

? 平均絕對誤差：

式中：N為樣本總數，dk,i表示樣本k的第i個神經元的預期輸出值，outk,i表示樣本k的第i個神經元的實際輸出值。最大均方誤差和最大平均絕對誤差分別指整個迭代過程中，均方誤差和平均絕對誤差的最大值。

表3 實驗結果評估標準

使用相同的訓練集和測試集進行實驗，表4展示了兩種神經網絡的收斂速度和誤差情況。與傳統后向傳播神經網絡相比，基于SCG算法的模糊神經網絡的收斂速度提高了92.5%，均方誤差降低了75.4%，平均絕對誤差降低了70.2%。實驗證明，基于SCG算法的模糊神經網絡不僅保證了網絡的穩定性，還提高了網絡的收斂速度和準確率。

表4 兩種人工神經網絡識別艾略特波浪模式的效果

6 結 語

本文介紹了后向傳播神經網絡、模糊神經網絡及艾略特波浪理論。提出基于傳統后向傳播神經網絡的艾略特波浪模式分類器，根據傳統后向傳播網絡的缺陷及金融市場的變化特性提出了改進方法——基于SCG算法的模糊神經網絡。通過實驗，比較了兩種分類識別艾略特波浪模式的方法的效果。實驗證明了利用人工神經網絡技術從金融時間序列中識別艾略特波浪模式的可行性。根據實驗數據得出結論，基于SCG算法的模糊神經網絡在收斂速度和準確率上的表現均比傳統后向傳播神經網絡更好。但是，本文的研究以專家經驗為基礎，采取啟發式方法選擇訓練和測試，這可能引入數據不平衡的問題。艾略特波浪理論提供了一個成熟可靠的金融市場分析方法，但國內對該理論的研究較少。目前，利用人工智能技術對金融時間序列的研究較多，缺乏結合艾略特波浪理論這一有效工具的研究。本文僅利用兩種神經網絡對艾略特波浪做了初步的分類識別，與實現將艾略特波浪理論與人工智能方法融合的目標還有一定差距。下一步將注重于調整網絡深度、優化網絡參數。考慮到分形理論是艾略特波浪理論的基礎，接下來還將嘗試結合分形網絡模型(FractalNet)實現艾略特波浪的識別。