基于鄰域組合熵的屬性約簡算法

王 光 瓊

(四川文理學院智能制造學院 四川 達州 635006) (達州智能制造產業技術研究院 四川 達州 635006)

0 引 言

粗糙集作為一種處理不確定性信息的有效數學工具，已經廣泛應用于機器學習、知識發現和規則提取等領域[1-3]。經典粗糙集以完備信息系統為研究對象，通過嚴格的等價關系對論域進行劃分，要求所有屬性值都是離散型的。然而，實際應用中，來自教育、醫療和金融等領域的數值型數據很多，經典粗糙集不能直接處理屬性值有數值型數據的信息系統，為了解決此問題，Lin[4]對等價關系進行擴展，提出了鄰域關系。鄰域關系能夠處理同時有名義性和數值型數據的混合型信息系統，因此基于鄰域關系的鄰域粗糙集模型得到廣泛應用[5-6]。

屬性約簡是粗糙集領域中研究的關鍵問題之一，目的是在不影響系統分類能力的前提下剔除冗余的條件屬性。為了對信息系統進行屬性約簡，從信息論的角度出發，文獻[7]提出了基于信息熵的決策表約簡算法;文獻[8]提出了基于條件信息熵的決策表約簡；文獻[9]提出了基于邊界域的條件信息熵屬性約簡算法。以上算法主要處理符號型數據，不能直接處理數值型數據或者符號性和數值型混合的數據。為了解決此問題，借助鄰域關系可以處理混合數據的特點，文獻[10]提出了一種基于鄰域熵的屬性約簡算法；文獻[11]提出了鄰域決策錯誤率的局部約簡算法；文獻[12]提出了基于鄰域組合測度的屬性約簡算法。此外，在粗糙集理論中，不確定性分為知識不確定性和集合不確定性。目前提出的屬性重要度度量大多僅考慮知識不確定性或者集合不確定性，同時考慮兩者的不確定性來定義屬性重要度度量進而設計屬性約簡算法是研究的熱點。

本文以鄰域信息系統為研究對象，以鄰域關系為基礎，為了描述知識對系統的劃分能力，首先定義了鄰域條件熵。為了從知識不確定性和集合不確定性兩個方面來綜合度量屬性的重要度，將鄰域條件熵與鄰域近似精度結合，定義了屬性重要度度量——鄰域組合熵，并提出了基于鄰域組合熵的屬性約簡算法。該算法可以處理離散型和數值型并存的不完備鄰域信息系統。最后實驗驗證了本文所提算法的有效性。

1 相關概念

特別地，若A=C∪D，C為條件屬性集合，D為決策屬性集合，則稱DNI=(U,C∪D,V,f,δ)為鄰域決策信息系統。若用“*”表示缺失值，?a∈A，存在f(x,a)=*，則稱NI為不完備信息鄰域信息系統。

定義2設鄰域信息系統NI=(U,A,V,f,δ)，定義屬性子集B?C上的δ的鄰域關系為：

NRδ(B)={(x,y)∈U×U|DB(x,y)≤δ}

(1)

式中：DB(x,y)表示對象x和y在屬性子集B上的距離。顯然，鄰域關系滿足自反性和對稱性。為了可以處理離散型和數值型并存的不完備鄰域信息系統，本文中的距離采用文獻[13]中的距離函數。設屬性子集B={a1,a2,…,am}，距離度量為：

式中：1≤l≤M。

當al為名義性屬性時：

當al為數值型屬性時：

定義3設鄰域信息系統NI=(U,A,V,f,δ)，?x∈U，x關于B的鄰域為：

(2)

性質1設鄰域信息系統NI=(U,A,V,f,δ)，?x∈U，對于P,Q?A，有：

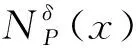
定義4設鄰域信息系統NI=(U,A,V,f,δ)，對象集X?U關于屬性子集B?C的上、下近似和邊界域分別定義如下：

(1)X的上近似：

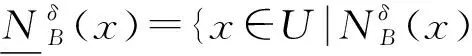
(3)

鄰域近似精度刻畫了信息系統中對象集合的不確定性，其值一般隨著屬性子集的增大而增大，因此成為一種重要的不確定度量工具。然而，鄰域近似精度并不具有嚴格的單調性，也存在屬性子集增大，其值不變的情況。

2 鄰域條件熵以及鄰域組合熵

為了從知識不確定性和集合不確定性兩個方面來度量屬性重要度，本節定義了鄰域條件熵，并結合鄰域近似精度定義了鄰域組合信息熵。

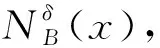
(4)

信息熵KN(B)反映了屬性子集B對系統論域中對象的區分能力，KN(B)的值越大，屬性子集的區分能力越好。

定義7設鄰域信息系統NI=(U,A,V,f,δ)，P,Q?C，知識Q關于P的鄰域條件熵定義為：

NE(Q|P)=NE(Q∪P)-NE(P)

(5)

鄰域條件熵NE(Q|P)反映了屬性集合P對于屬性集合Q的不確定性。對于決策鄰域信息系統，NE(D|P)則反映了屬性集P對于決策屬性D的不確定性。

證明:NE(Q|P)=NE(Q∪P)-NE(P)=

定理2(單調性) 設鄰域信息系統NI=(U,A,V,f,δ)，P,Q?C，P?Q，則有NE(D|Q)≤NE(D|P)。

證明:NE(D|P)-NE(D|Q)=

定理2表明，鄰域條件熵具有單調性，熵值隨著條件屬性集合的增大而減小，條件信息熵越小，則系統協調程度越高。因此在屬性約簡中，鄰域條件熵可以作為屬性重要度度量的一個重要因素。

其實，屬性重要度的度量主要有基于代數定義和基于信息定義的方法[14]。兩種方法具有互補的特性，基于代數定義主要考慮的是屬性對論域中確定分類子集的影響；基于信息定義主要考慮的是屬性對于論域中不確定分類子集的影響。為了同時從基于代數定義和基于信息定義兩個方面衡量屬性重要度，結合鄰域近似精度和鄰域條件熵定義新的鄰域組合熵。

(6)

鄰域近似精度從集合的角度考慮不確定性，鄰域條件熵從知識的角度考慮不確定性，因此鄰域組合熵同時考慮了集合和知識的不確定性，對不確定性的刻畫更加全面。

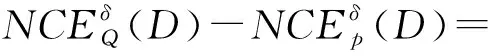
定理3表明，鄰域組合熵具有單調性，熵值隨著條件屬性集合的增大而增大。因此，可以以鄰域組合熵來度量屬性的重要度，設計基于鄰域組合熵的屬性約簡算法。

定義9設鄰域決策信息系統NI=(U,C∪D,V,f,δ)，?B?C，對于屬性a∈C-B，a相對于B的重要性定義為：

(7)

定義10設鄰域決策信息系統NI=(U,C∪D,V,f,δ)，?B?C，若滿足如下條件：

則稱屬性子集B為C相對于決策屬性的一個相對約簡。

定義11對于一個鄰域信息系統NI=(U,C∪D,V,f,δ)，相對于決策屬性D，C中所有必要的屬性組成的集合稱為C相對于D的核，簡稱相對核。

3 基于鄰域組合熵的屬性約簡算法(ARNCE)

本節以鄰域組合熵為啟發信息，提出了一種鄰域信息系統的屬性約簡算法。

算法1為計算鄰域組合熵的算法。

算法1鄰域組合熵的計算

Step 1 計算鄰域條件熵；

foriton

計算p(xi),

Endfor

計算鄰域信息熵NE(B)；

計算鄰域條件熵NE(D|B)；

Step 2 計算鄰域近似精度；

forjtom，

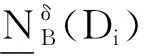
Endfor

算法2為基于鄰域組合熵的屬性約簡算法。算法思想：以空集合為起點，以鄰域組合熵對屬性重要度的度量作為啟發信息，每次選擇重要度最大的屬性加入約簡集，直到所有未被選擇的屬性都是不重要的。

算法2基于鄰域組合熵的屬性約簡算法

輸出：約簡集合RED。

Step 1 初始化RED=?；

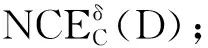
Step 3 Do

對于?ai∈C-RED，根據算法1計算Sig(ai,RED,D)，

If

Sig(amax,RED,D)=max{Sig(ai,RED,D)|ai∈C-RED}

RED=RED∪{amax}，

Endif

UntilSig(amax,RED,D)=0

Step 4 返回RED；

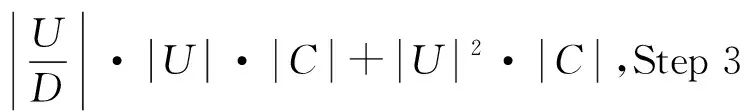
4 實驗結果分析

為了驗證本文所提算法處理鄰域信息系統的可行性，將本文的算法與以下幾種算法分別從屬性約簡數量和分類精度方面進行比較。

1) 基于鄰域依賴度的屬性約簡算法(DNFS)[15];

2) 基于鄰域條件熵的屬性約簡算法(ARCE)[16];

3) 基于鄰域組合測度的屬性約簡算法(ARNCM)[12]。

由于在屬性約簡時算法DNFS只考慮依賴度，算法ARCE只考慮了條件熵，而算法ARNCM同時考慮了粒度測度和近似精度。本文算法同時考慮了信息熵和近似精度，所以算法ARNCM和本文算法的時間復雜度要高于DNFS和ARCE。本節主要比較各算法約簡后的屬性約簡數量和分類精度。

本文算法采用Java語言編程實現，硬件環境為：intel處理器3.7 GHz，內存2 GB。

選用UCI中的6個數據集進行實驗，其中4個完備數據集，2個不完備數據集。在屬性類型方面，數據集Heart、Hepatitis的屬性為混合型，數據集Zoo、Soybean的屬性為符號型，數據集Wdbc、Sonar的屬性為數值型，數據集的具體信息見表1。為了消除各屬性量綱不一致對鄰域計算的影響，在實驗前，對數據集中所有的數值型屬性進行標準化處理，統一標準化到[0,1]區間。鄰域參數設置為δ=0.15。

表1 UCI數據集中的六個數據集

首先比較各算法屬性約簡之后的屬性約簡集大小，實驗結果如表2所示。由表2可知，所有算法都能有效地對數據集進行屬性約簡。算法ARNCE與算法DNFS、ARCE相比，在所有數據集上都獲得了相等或者較小的屬性約簡集。算法ARNCE和算法ARNCM屬性約簡集大小較為接近，通過對6個數據集的屬性約簡集大小進行平均計算，算法ARNCM的平均屬性約簡集大小為6.66，算法ARNCE的平均屬性約簡集大小為6.33。總體而言，相比較于另外三種屬性約簡算法，本文所提算法ARNCE能夠獲得約簡集較小的屬性約簡結果。

表2 不同算法屬性約簡后屬性約簡集大小

為了進一步驗證屬性約簡算法的有效性和分類能力，實驗中通過支持向量機(SVM)和決策樹(C4.5)兩種分類器，采用十折交叉驗證的方法，比較各算法約簡之后的分類精度，實驗結果如表3和表4所示。

表3 基于SVM算法的分類精度比較

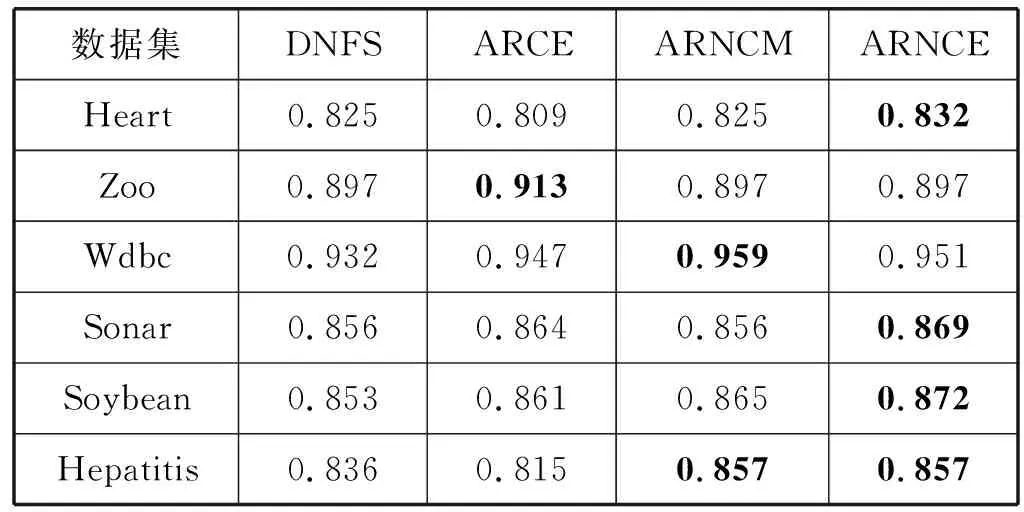
表4 基于C4.5算法的分類精度比較

由表3和表4可知：

1) 對于兩個混合型數據集Heart、Hepatitis，關于數據集Heart，本文算法ARNCE約簡后的分類精度最高；關于數據集Hepatitis，本文算法ARNCE和ARNCM約簡后的分類精度相等并且都高于算法DNFS、ARCE。

2) 對于兩個數值型數據集Wdbc、Sonar，關于數據集Wdbc，在SVM下本文算法ARNCE約簡后的分類精度較高，在C4.5下算法ARNCM約簡后的分類精度較高；關于數據集Sonar，在SVM下算法ARNCM約簡后的分類精度較高，在C4.5下本文算法ARNCE約簡后的分類精度較高。

3) 對于兩個符號型數據集Zoo、Soybean，關于數據集Zoo，算法ARCE約簡后的分類精度較高；關于數據集Soybean，本文算法ARNCE約簡后的分類精度較高。

從整體上看，相比于算法DNFS、ARCE和ARNCM，本文提出的算法ARNCE對大部分數據集進行屬性約簡后的分類精度較高。

綜合上述實驗結果可知，本文算法ARNCE能夠對鄰域信息系統進行有效約簡，且能夠獲得約簡集較小、分類精度較高的屬性約簡結果。

5 結 語

以鄰域信息系統為研究對象，本文從信息論角度出發，定義了鄰域信息熵和鄰域條件熵。結合鄰域條件熵和近似精度，定義了鄰域組合熵，可以綜合知識不確定性和集合不確定性對鄰域信息系統屬性重要度進行度量，給出并證明了鄰域組合熵的相關定理。基于鄰域組合熵，提出了鄰域信息系統中的屬性約簡算法。實驗結果表明該算法能夠獲得約簡集較小而分類精度較大的約簡結果。在關于鄰域信息系統的屬性約簡算法中，鄰域參數δ的選取，對約簡結果有著很大影響，下一步將對鄰域參數δ選取進行研究。