神經網絡自適應噪聲抵消系統的性能比較與仿真

張 磊 李方鑫 王建新 肖超恩

(北京電子科技學院 北京 100070)

0 引 言

自適應噪聲抵消系統的基本要求是原始輸入和參考輸入中信號必須統計相關[1]。在傳統的抵消算法中，要求噪聲滿足線性相關的條件。然而在現實中，噪聲通道往往十分復雜，具有非線性的特性；當兩路輸入噪聲非線性相關時，傳統的自適應噪聲抵消算法(LMS、NLMS、RLS)[2-5]去噪效果難以保證，甚至產生信號失真。因此，需要尋找一種有效應對噪聲非線性相關的自適應噪聲抵消方法。

神經網絡[6-7]利用大量的人工神經元相互連接進行計算，根據外界的信息改變自身的結構，主要通過調整神經元之間的權值來對輸入的數據進行建模，最終具備解決實際問題的效果。目前，在人工神經網絡的實際應用中，絕大多數的神經網絡模型都采用BP網絡及其變化形式，它是前饋型神經網絡的核心部分[8]。近年來，已有部分研究將神經網絡應用于自適應噪聲抵消系統中，在有源噪聲控制方面取得了一定的效果。

2010年，Miry等[9]提出了一種基于模糊神經網絡[10]的自適應噪聲消除算法，該算法用于長距離通信信道的噪聲消除，系統的主要優點是易于實施和快速收斂。2010年，李曉艷[11]將基于神經網絡的自適應噪聲抵消器與基于LMS算法的自適應噪聲抵消器進行對比，在兩路噪聲信號線性和非線性相關時進行了性能比較。結果表明基于神經網絡的自適應噪聲抵消器在兩路信號線性相關和非線性相關時，均具有良好的噪聲抵消能力。2011年，蔣威等[12]為了提高無線電引信的抗干擾性，采用量子神經網絡建立自適應干擾對消系統，實現對無線電引信干擾噪聲的自適應抵消，提高了無線電引信的抗干擾性。2012年，周偉等[13]研究了基于最小均方誤差LMS準則、遞推最小二乘RLS準則和線性神經網絡ADALINE[14]的三種自適應噪聲抵消算法。結果表明，采用ADALINE算法信噪比至少改善26.6 dB，實現了高性能濾波。2014年，Dixit等[15]利用神經網絡實現了基于最小均方自適應濾波器算法(LMS)的自適應噪聲抵消器，提出了自適應噪聲抵消器的系數通過神經網絡而不是數值自適應算法進行調整的方法。與直接使用LMS作為自適應算法相比，使用神經網絡調整系數后的LMS算法，收斂速度更快。但是相關文獻均沒有考慮神經網絡結構的變化對噪聲抵消效果的影響。

本文基于上述問題，分別在原始輸入和參考輸入中，噪聲線性相關和非線性相關的條件下，研究神經網絡自適應噪聲抵消系統不同隱含層神經元節點數、不同隱含層傳輸函數、不同神經網絡學習算法以及不同信噪比原始輸入下，系統的噪聲抵消效果。

1 神經網絡自適應噪聲抵消系統基本原理

神經網絡自適應噪聲抵消系統的噪聲抵消原理如圖1所示，噪聲和信號沿信道傳到傳感器A、B中。除了接收到信號s之外，傳感器A還接收到一個不相關的噪聲n1。信號加噪聲為s+n1，組成抵消系統的“原始輸入”。傳感器B用來接收與信號不相關的，但是以某種未知的方式與噪聲n1相關的噪聲n0，這個傳感器給系統提供“參考輸入”。將噪聲n0通過神經網絡自適應濾波系統加以調整，使其產生近似為n1的輸出y。再將該輸出從原始輸入s+n1中減去，得到系統輸出為z=s+n1-y。

圖1 神經網絡算法自適應噪聲抵消系統

噪聲源的噪聲n0經過實際環境得到噪聲n1，兩路噪聲(n0和n1)往往是非線性的，可以用非線性變換來模擬實際中噪聲所經過的通道。要想得到濾波器的輸出y，必須盡可能地辨識出該非線性函數，相當于獲得自適應神經網絡，使得在獲得噪聲源n0的條件下，自適應神經網絡無限逼近非線性變換函數，此時y就能無限逼近原始輸入中的噪聲n1。現實條件中，由于n1難以獲得，而傳感器A能得到d，且d為信號s與n1的疊加，s與n1不相關，所以利用d替代n1對網絡進行訓練，完成對噪聲通道的模擬，得到系統輸出為z=d-y，達到噪聲抵消的目的。

2 自適應噪聲抵消系統的模型

2.1 輸入信號模型

噪聲抵消系統的輸入信號分為兩個部分：原始輸入和參考輸入。根據文獻[11]提出的參考輸入與原始輸入中，噪聲信號相關性的模型，在MATLAB R2014a環境下對兩路輸入信號進行建模，如圖2所示。設原始輸入為50 Hz單頻信號和randn函數產生的服從正態分布的隨機噪聲信號的線性疊加，采樣頻率為1 kHz。

圖2 兩路噪聲信號建模

根據圖2的模型，在兩路噪聲線性相關條件下，設參考輸入n1與原始輸入中噪聲信號n0的關系為線性變換n0=n1+1。在兩路噪聲非線性相關條件下，設參考輸入n1與原始輸入中噪聲信號n0的關系為非線性變換n0=sin(n1)。

2.2 BP神經網絡模型

根據圖1的噪聲抵消模型，本文采用的單輸入單輸出BP神經網絡結構如圖3所示。BP神經網絡輸入層、隱含層、輸出層的層數各為一層。輸入層節點數和輸出層節點數為1，隱含層節點數為N。

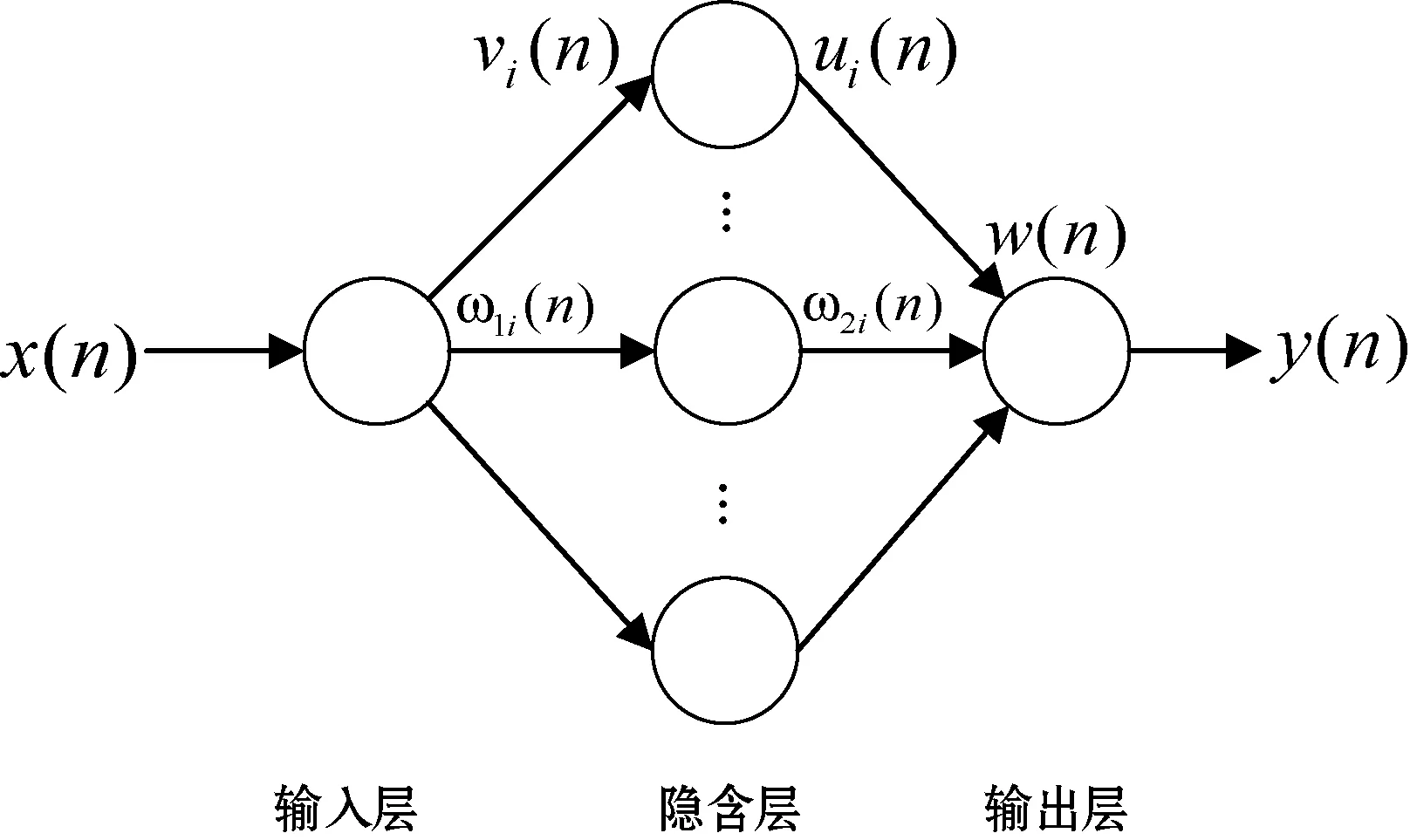
圖3 BP神經網絡結構

輸入層節點的輸出等于整個網絡的輸入信號x(n)，隱含層第i個神經元節點的輸入vi(n)等于權向量ω1i(n)與x(n)的乘積：

vi(n)=ω1i(n)x(n)

(1)

假設f(·)是隱含層傳輸函數，則隱含層第i個神經元的輸出等于：

ui(n)=f(vi(n))

(2)

輸出層節點的輸入等于權向量ω2i(n)與ui(n)的加權和：

(3)

假設g(·)是輸出層傳輸函數，輸出層神經元的輸出等于：

y(n)=g(w(n))

(4)

網絡的總誤差為：

e(n)=d(n)-y(n)

(5)

式中：d(n)為期望信號。

2.3 噪聲抵消系統的評價指標

若按照信號功率來計算信噪比[16]，自適應噪聲抵消系統的輸入信噪比為原始輸入信號中的有用信號s的功率與干擾噪聲n0的總功率之比，并將結果取以10為底數的對數，即：

(6)

輸出信噪比為有用信號s與經過噪聲抵消系統的剩余噪聲z-s總功率之比，將結果取對數：

(7)

式中：z為噪聲抵消系統的輸出信號。

本文定義信噪比增量ΔSNR為：

ΔSNR=SNRout-SNRin

(8)

3 仿真分析

根據前述模型，分別對不同隱含層節點數、不同神經網絡學習算法、不同隱含層傳輸函數和不同信噪比原始輸入下系統的噪聲抵消效果進行仿真分析。

在MATLAB R2014a環境下，使用newff函數創建一個結構為1-N-1的BP神經網絡(N表示隱含層節點數)。網絡的隱含層使用tansig或logsig函數，輸出層使用purelin型線性函數，訓練過程的學習速率取為0.01，期望誤差值為0.01，學習算法[17]使用GD(標準梯度下降算法)、GDM(帶動量的梯度下降算法)、GDA(可變學習速率梯度算法)、RP(彈性梯度算法)、LM(Levenberg-Marquardt算法)、BFG(擬牛頓算法)、OSS(一步正割算法)。

3.1 改變隱含層節點數

隱含層節點數對BP神經網絡性能有很大影響。一般較多的隱含層節點數可以帶來更好的性能，但會導致訓練時間過長。目前并沒有一個理想的解析式可以用來確定合理的神經元節點數，通常的做法是采用經驗公式給出估計值[18]。

本節中，神經網絡學習算法使用LM算法，網絡的隱含層使用tansig函數，改變隱含層節點數，對噪聲抵消系統進行仿真。

原始輸入和參考輸入中，噪聲線性相關時(兩路噪聲線性相關)，進行10次實驗并對結果取平均值后，仿真結果如圖4所示。設定原始輸入信號信噪比為-0.87 dB，輸出信號信噪比隨隱含層節點數增加呈下降趨勢。在本節仿真的1-N-1網絡結構中，當隱含層節點數為1個時，輸出信號信噪比為26.24 dB，輸出信號與原始輸入的ΔSNR為27.11 dB，達到最佳的噪聲抵消效果。

圖4 隱含層節點數仿真結果圖

在兩路噪聲線性相關的條件下，根據實驗結果，優化的單輸入單輸出BP神經網絡隱含層節點數的公式為：

(9)

式中：取值范圍為[0,5]的整數，計算結果向0取整。

原始輸入和參考輸入中，噪聲非線性相關時(兩路噪聲非線性相關)，進行10次實驗并對結果取平均值后，仿真結果如圖5所示。設定原始輸入信號信噪比為0.42 dB，輸出信號信噪比隨隱含層節點數增加呈下降趨勢。在本節仿真的1-N-1網絡結構中，當隱含層節點數為1時，輸出信號信噪比為4.76 dB，輸出信號與原始輸入的ΔSNR為5.18 dB，達到最佳的噪聲抵消效果。

圖5 隱含層節點數仿真結果圖

在兩路噪聲非線性相關的條件下，根據實驗結果，優化的隱含層節點數的經驗公式與式(9)相同。

3.2 改變學習算法

使用式(9)，在兩路噪聲線性相關和非線性相關的條件下，本節將隱含層節點數q確定為3。網絡的隱含層使用tansig函數，神經網絡學習分別使用GD、GDM、GDA、RP、BFG、LM、OSS算法，進行仿真。

兩路噪聲線性相關時，設定原始輸入信號信噪比為-5.58 dB，經過神經網絡噪聲抵消系統后，輸出的信號信噪比如圖6所示。對仿真結果取10次平均后，神經網絡學習算法改善效果依次為：

OSS>LM>BFG>RP>GDA>GDM>GD

其中，OSS、LM、BFG和RP四種學習算法對原始輸入信號的ΔSNR都超過了25 dB，噪聲抵消效果明顯優于其他3種算法。

圖6 神經網絡學習算法仿真結果圖

兩路噪聲非線性相關時，設定原始輸入信號信噪比為-3.34 dB，經過神經網絡噪聲抵消系統后，輸出信號的信噪比如圖7所示。在兩路輸入非線性相關時，神經網絡噪聲抵消器的改善效果較兩路輸入線性相關時較弱，7種學習算法中對原始輸入信號的ΔSNR最大為6.70 dB(BFG)，且經過各學習算法噪聲抵消后的輸出信號平均信噪比為3.11 dB，噪聲抵消效果差別不大。

圖7 神經網絡學習算法仿真結果圖

3.3 改變傳輸函數

logsig函數的特點是(-∞，+∞)范圍的數據被映射到區間(0，1)，使用的計算公式為:

(10)

tansig函數是雙曲正切sigmoid函數，在tansig函數中，輸出被映射在(-1,1)內。計算公式為:

(11)

神經網絡學習使用GD、GDA、GDM、LM、OSS、RP、BFG算法，根據式(9)，在兩路噪聲線性相關和非線性相關的條件下，本節將隱含層節點數q確定為3，對網絡的隱含層分別使用logsig、tansig函數進行仿真。各組仿真實驗進行10次，并對結果取平均值。

兩路噪聲線性相關時，設定原始輸入信號信噪比為-3.43 dB，仿真結果如圖8所示。神經網絡學習使用GD和GDM算法，經過不同傳輸函數得到的輸出信號之間的SNR差值大于3 dB；GDA、LM、OSS、RP和BFG算法經過不同傳輸函數得到的輸出信號之間的SNR差值小于1 dB。結果表明，神經網絡學習使用GD和GDM算法時，相比logsig函數，噪聲抵消系統使用tansig作為傳輸函數得到的輸出信號，噪聲抵消效果顯著；其余五種算法由傳輸函數的差異產生的噪聲抵消效果差別不大。

圖8 傳輸函數仿真結果圖

兩路噪聲非線性相關時，設定原始輸入信號信噪比為-2.50 dB，仿真結果如圖9所示。神經網絡訓練使用GD和GDM算法，經過不同傳輸函數得到的輸出信號之間的SNR差值小于1.3 dB；GDA、LM、OSS、RP和BFG算法經過不同傳輸函數得到的輸出信號之間的SNR差值小于0.5 dB。結果表明，兩路噪聲非線性相關時，噪聲抵消系統使用tansig作為傳輸函數得到的輸出信號，ΔSNR較大，噪聲抵消效果較好；其余五種算法由傳輸函數的差異產生的噪聲抵消效果差別不大。

圖9 傳輸函數仿真結果圖

3.4 不同信噪比原始輸入下的噪聲抵消效果

兩路噪聲線性相關和非線性相關時，根據式(9)，將隱含層節點數q確定為3，隱含層傳輸函數使用tansig。設定原始輸入為不同信噪比的信號，在兩路噪聲線性相關和非線性相關的條件下，比較使用BFG、GD、GDA、LM學習算法的噪聲抵消效果。

兩路噪聲線性相關時，噪聲抵消系統的原始輸入和經神經網絡不同算法訓練后，輸出信號信噪比如圖10所示。原始輸入信號的信噪比取-10～0 dB中的值，經過系統噪聲抵消后，各算法輸出信號信噪比至少提高了2 dB，且隨著原始輸入信號信噪比的提高，系統的輸出信號信噪比也在提高。結果表明，兩路噪聲線性相關時，神經網絡噪聲抵消系統對信噪比小于0 dB的輸入信號有顯著的噪聲抵消效果。

圖10 系統的噪聲抵消效果

兩路噪聲非線性相關時，噪聲抵消系統的原始輸入和經神經網絡不同算法訓練后，輸出信號的信噪比如圖11所示。原始輸入信號的信噪比取2～10 dB中的值，經過系統噪聲抵消后，各算法輸出信號信噪比平均提高了1～1.5 dB，且隨著原始輸入信號信噪比的提高，系統的輸出信號信噪比也在提高。結果表明，兩路噪聲非線性相關時，神經網絡噪聲抵消系統對信噪比大于0 dB的輸入信號有良好的噪聲抵消效果。

4 結 語

BP神經網絡具有非線性映射和學習的能力，可用于噪聲抵消系統中噪聲的非線性建模。本文利用BP神經網絡組成自適應噪聲抵消系統，在原始輸入和參考輸入中噪聲線性相關和非線性相關的條件下，研究了不同隱含層節點數、不同神經網絡學習算法、不同隱含層傳輸函數對系統噪聲抵消效果的影響，并優化了噪聲抵消系統中單輸入單輸出BP神經網絡隱含層節點公式。在不同信噪比原始輸入下，比較了系統的噪聲抵消效果。從仿真結果可知，系統的噪聲抵消效果受到隱含層節點數的影響；在隱含層傳輸函數選擇上，建議使用tansig作為傳輸函數；在原始輸入和參考輸入中噪聲線性相關時，神經網絡噪聲抵消系統對信噪比小于0 dB的輸入信號有顯著的噪聲抵消效果；兩路輸入中噪聲非線性相關時，系統對信噪比大于0 dB的輸入信號有提高信噪比的效果。噪聲抵消系統中BP神經網絡采用優化后的隱含層節點數公式，具有很強的降噪能力，可用于低信噪比下噪聲抵消。