基于CPD-SMOTE的類不平衡數據分類算法研究

彭如香 楊 濤 孔華鋒 姜國慶 凡友榮

(公安部第三研究所 上海 201204) (信息網絡安全公安部重點實驗室 上海 201204)

0 引 言

類不平衡是指屬于某一類別的觀測樣本的數量顯著少于其他類別，通常情況下把多數類樣本的比例為100∶1、1 000∶1，甚至是10 000∶1這種情況下為不平衡數據[1]。類不平衡現象普遍存在著不同應用領域中，如金融欺詐、網絡入侵、垃圾郵件過濾、醫學檢測，直接采用傳統的學習分類算法，分類準確率較低[1-3]。通常采用重采樣方法處理類不平衡問題,重采樣包括欠采用和過采樣兩種[1]。相比于傳統欠采樣方法，SMOTE算法克服傳統隨機欠采樣導致的數據丟失問題。但是，SMOTE容易出現過泛化和高方差的問題，進而影響數據分布特征。為了解決這些問題，Borderline-SMOTE、ADASYN、LN-SMOTE等SMOTE改進算法相繼被提出[4-6]。這些算法充分考慮小樣本的分布，新增的樣本不影響小樣本的分布。然而這些算法未考慮小樣本與大樣本的交叉區域，最終形成的數據集將改變原有數據集的分布，而影響分類算法的準確性。

1 相關工作

1.1 SMOTE算法

SMOTE，即合成少數類過采樣技術[1]。該算法由Chawla于2002年提出，是對隨機過采樣算法的一種改進。SMOTE算法的基本思想是對少數類樣本進行分析和人工模擬，同時將模擬得到的新樣本數據添加到原始數據集當中，使得數據正負樣本比例均衡。

SMOTE算法流程如下：

(1) 對于少數類樣本中每一個樣本x，通過計算x到該類樣本集所有樣本的歐式距離，利用KNN算法，選出離樣本x最近的k個同類樣本點，得到其K近鄰。

(2) 根據正負樣本比例確定采樣倍率為N，對每一個樣本x分別隨機從K近鄰中選取N個樣本，假設選擇的近鄰為x1,x2,…,xN。

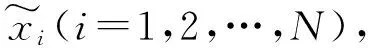
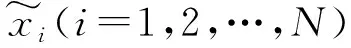
SMOTE算法的出現，改進了處理非平衡數據中傳統的隨機過采樣算法，可以有效地對非平衡數據進行糾偏，整體上提高了模型的精度，同時還很大程度上降低了模型的誤識率，這是SMOTE算法的優點[9]。其缺陷是無法解決非平衡數據的分布問題，容易產生分布邊緣化問題，對于邊緣的少類樣本，對其進行K近鄰生成樣本也位于邊緣且會越來越邊緣化，這會使得正負樣本的邊界越來越模糊，加大樣本分類的難度。

1.2 類不平衡算法評價指標

根據不同的應用場景，分類器考慮的評價指標也不同，通常基于混淆矩陣進行性能評價。混淆矩陣的定義如表1所示[7]：

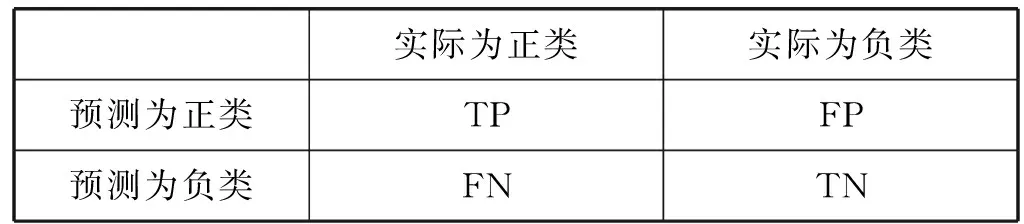
表1 混淆矩陣定義

使用混淆矩陣可以得到如下幾個評價指標：

精確度Accuracy=(TP+TN)/(TP+FN+FP+TN)

召回率R=TP/(TP+FN)

準確度P=TP/(TP+FP)

召回率和準確度通常會出現矛盾，這樣需要綜合考慮，最常見的方法就是F-Measure(又稱為F-Score)。 F-Measure是Precision和Recall加權調和平均，其定義如下：

另外，可以通過ROC曲線評價一個分類器好壞。ROC曲線是基于樣本的真實類別和預測概率來畫的，具體來說，ROC曲線的x軸是偽陽性率(FP/(TN+FP))，y軸是真陽性率(TP/(TP+FN))；AUC(Area Under Curve)被定義為ROC曲線下的面積。簡單地說，AUC值越大的分類器，正確率越高。

2 CPD-SMOTE類不平衡數據處理算法

通過上述介紹，SMOET算法充分考慮小樣本的分布，新增的樣本不影響小樣本的分布。然而該算法未考慮小樣本與大樣本的交叉區域，最終形成的數據集將改變原有數據集的分布，而影響分類算法的準確性[5-6]。

本文提出一種改進型SMOET——CPD-SMOTE。CPD-SMOTE通過考慮訓練集小樣本Si的特征、位置及其周圍樣本分布，來確定Si的強相關鄰居集SCNi。以SCNi作為SMOTE最近鄰居集，產生新的小樣本。這里強相關鄰居集SCNi滿足：

1)SCNi每個元素都為小樣本特征向量；

2) 對于SCNi每個元素Ck，Ck與Si組成的超矩陣中不包含大樣本特征向量。

其算法如下：

算法1強相關鄰居集確定算法

輸出：所有小樣本的強相關鄰居集{SCN1，SCN2,…,SCNs}。

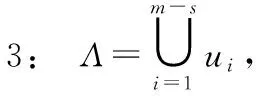
4: i=1;

5: For j in[2,s]

6: 判斷zi與zj組成超矩陣中，是否包含Λ中的值；

7: 若不包含，則將zj加入到SCNi集合中；

8: Fori in[2,s-1]

9: For j in[1,i-1]

10: 判斷SCNj中是否包含zi

11: 若包含，則將zi加入到SCNj集合中；

12: For j in[i+1,s]

13: 判斷zi與zj組成超矩陣中，是否包含Λ中的值；

14: 若不包含，則將zj加入到SCNi集合中；

15: i=s;

16: For j in[1,s-1]

17: 判斷SCNj中是否包含zi

18: 若包含，則將zi加入到SCNj集合中；

19: 若不包含，則將zj加入到SCNi集合中；

20: 計算非空強相關鄰居集中元素數量平均值k;

21: 對于所有為空的強相關鄰居集SCNi

22: 從大樣本集Λ中隨機挑選k個zi(小樣本)的最近鄰居Λ′

23: 對于Λ′中的所有uj

24: 取α為n維向量，元素取值為[0,0.5]之間的隨機值；

25:znew=zi+(uj-zi)×α

26: 將znew加入到SCNi中

下面通過二維圖簡單說明強相關鄰居節點選擇方法，如圖1所示。

圖1 小樣本x1的強相關鄰居節點選擇示意圖

圖1中，實心圓表示小樣本節點，空心圓表示大樣本節點。通過上述強相關鄰居集確定算法，判斷x2是否是x1的強相關節點的依據是由x2與x1組成的超矩陣中，是否包含大樣本節點確定的。從圖中看出x2滿足該條件，故可將x2加入x1的強相關鄰居集SCN1中。同理，x3也為SCN1的元素，而x4將不會被選到SCN1中。雖然x4到x1的距離小于x3,但是x4與x1之間存在大樣本節點。若不考慮大樣本節點的存在，采用傳統的SMOTE,在x4與x1連線上隨機產生新的節點，將影響大樣本的分布，進而影響整個樣本空間的分布。采用本文中的提出強相關鄰居集確定算法，x4將不會被納入到SCN1。然后，將SCN1作為SMOTE算法中鄰居集產生新的小樣本節點仍服從原來的分布。對于x5，根據上述判斷條件，將不存在符合條件的鄰居，所得到的強相關鄰居集為空。考慮到這種情況，本算法充分考慮節點鄰居數量均衡的特點，首先計算非空強相關鄰居集中元素數量平均值k，然后從大樣本集中隨機挑選k個x5最近鄰居，其次從x5與每個鄰居的連線不超過一半(x5為起點)上隨機挑選一個點作為x5的強相關鄰居。至此，每個小樣本的強相關鄰居集都已確定。接下來將得到的強相關鄰居集作為SMOTE算法中鄰居集，完成新樣本的生成，其算法過程如下：

算法2CPD-SMOTE算法

1: 設α為n維向量，元素取值為[0,1]之間的隨機值；

2: 使用上述強相關鄰居集確定算法，得出強相關鄰居集{SCN1，SCN2,…,SCNs}

3: Fori從1到N

4: 隨機挑選小樣本Φ中的點zj：

5: 對于SCNi中元素zj

6:znew=zi+(zj-zi)×α

7: 將這些新的點加入S中

3 實驗設置與分析

3.1 實驗數據

本文實驗采用來自Kaggle上的兩個數據集，paySim和CreditCard Fraud Detection。

數據集paySim一種移動金融交易數據數據集，該數據集包括總樣本數6 362 620個，其中正常交易樣本數為6 354 407，欺詐交易樣本數為8 237個，比例為772∶1。paySim數據集字段表如表2所示。

表2 字段含義表

數據集CreditCard Fraud Detection為信用卡交易數據。該數據集包含兩天內發生的交易，其中284 807筆交易中有492筆被盜刷。數據集為不平衡數據集，類(被盜刷)占所有交易的0.172%。它只包含作為PCA轉換結果的數字輸入變量。該數據集屬性除了時間和金額保留原始值，其他屬性采用PCA轉換進行了變換，轉換特征V1，V2，…,V28，特征“Class”為響應變量，如果發生被盜刷，則取值1，否則為0。

通過上述分析，這兩類數據均為不平衡數據集。

3.2 實驗分析

paySim數據集和CreditCard Fraud Detection數據集都給出了目標列，為監督學習的應用場景。是否是欺詐交易或信用卡是否被盜刷是一個二元分類問題，本文選用基分類算法是支持向量機SVM算法作為基分類器[7-8]。

為了驗證CPD-SMOTE算法與其他幾種類不平衡處理算法SMOTE、Borderline-SMOTE、ADASYN、LN-SMOTE的性能，本文構建的分類算法模型首先分別通過這些算法將數據進行類平衡處理，使得數據正負樣本比例均衡。然后分別采用SVM算法對數據分類，并采用10倍交叉驗證方法驗證模型的性能。這里SVM算法采用skik-learn算法集中，表3-表5分別給出了不同算法在兩個數據集上評測指標均值，包括召回率R、F-Measure與AUC均值。實驗結果表明，相比其他類平衡處理算法，CPD-SMOTE算法效果明顯，學習性能更優。

表3 基分類器為SVM下的不同算法的召回率R均值

表4 基分類器為SVM下的不同算法的F-Measure均值

表5 基分類器為SVM下的不同算法的AUC均值

4 結 語

針對類不平衡情況對分類器的影響，本文在SMOTE算法的基礎上，提出了CPD-SMOTE算法。該算法通過考慮訓練集小樣本的特征、位置及其周圍樣本分布，來確定小樣本的強相關鄰居集，以此作為SMOTE最近鄰居集，產生新的小樣本，實現數據正負樣本比例均衡，并采用SVM算法對數據進行分類預測。在相同的基分類器SVM情況下，相比其他4種算法(SOMTE、Borderline-SMOTE、ADASYN、LN-SMOTE)，CPD-SMOTE算法在處理不平衡問題時能提升分類性能。