港口集裝箱裝卸作業的Q-learning動態定價策略研究

余 玨 丁 一 林國龍

(上海海事大學物流研究中心 上海 201306)

0 引 言

國內港口的費率表主要是對不同箱型下各種尺寸的集裝箱的裝卸作業費用、中轉費用等的描述。就港口裝卸作業方面來看，港口企業在實際運作過程中會根據服務對象(集裝箱)類型提出相應的收費標準(費率)，而這個收費標準相對來說是固定不變的。因此，國內港口均存在內外貿費率偏低且港口費率長期不變的問題，而國際港口的費率每年隨市場變化進行調整。我國港口費率(即價格)長期不動導致雙方差距逐漸增大，不利于港口經濟發展。所以，我國港口也需要隨市場變化調整費率，以縮減我國港口與國際港口間的差距，促進港口經濟的發展。因市場變化由多種因素造成，包括有港口企業間的競爭關系，船公司的需求等。本文僅以船公司所提出的需求作為市場變化的衡量指標，從單船裝卸作業時間的層面探討研究在需求變化的前提下港口的定價決策問題。裝卸利潤是指港口企業的基本業務利潤，約占港口企業總利潤的80%以上，其變動的主要原因有裝卸操作量、平均單位收入、單位成本等。定價策略的優劣會直接影響港口企業(為不同的船公司提供服務后)的裝卸利潤。在此前提下，本文將單船裝卸作業時間作為需求，以單船裝卸利潤最大化為主要目標，研究港口在需求不斷變動的環境下的定價策略，從而促進企業經濟的發展，有效提高港口企業的競爭力。

根據研究意義可以看出，港口進行動態定價決策具有一定的實際意義。本文將研究有關港口企業的動態定價問題，分別對國內港口定價問題的相關研究和國內外動態定價的相關研究進行綜述說明，從而得知動態定價問題的現有研究內容、方法和應用領域等。根據綜述內容，本文將選擇合適的方法并應用在國內港口企業中。

關于港口定價問題的研究：文獻[1]使用運輸成本優化模型估計潛在需求。文獻[2]結合了兩種工具來研究印度加爾各答危機港口系統，構建船舶行為微觀經濟模型;使用適當非線性方程的雙重價格計算全均衡需求彈性(彈性)，將其與預期的利潤最大化行為的基準值進行比較。文獻[3]重點介紹了集裝箱港口優化空間分配和最優定價的優先制度確定；考慮貨物的內在、物流貨物價值和集裝箱各種要求的能力約束建立模型。模型在各個方向上擴展了經典價格差異理論，即反彈性規則。周鑫等[4]在改進的Hotelling模型基礎上,構建雙壟斷港口企業的定價模型,以實例說明港口企業采用差別定價策略的動機。劉文忠[5]認為我國市場化導向的價格規制改革仍不完善，進一步改革的方向將集中在目前規制較為嚴格的外貿運輸方面，應實行價格上、下限制。匡海波等[6]深入探討低碳轉型下的港口質押貸款利率決策理論,借助看跌期權反映客戶違約風險、質押貨物的碳排風險，采用VaR方法界定港口存貨類質押率；建立低碳港口流動性較強存貨類物流質押貸款利率決策模型。汪挺松等[7]針對目前船舶在港碳排放高的現象,提出引入價格補償機制的港航合作模式：通過價格補償機制對港方和船方在港航合作模式中的收益與損失進行分配。

關于國內外動態定價問題的研究：文獻[8]采用了啟發式算法研究標準的動態定價問題。文獻[9]主要解決多目標動態定價問題。文獻[10]使用時間歸一化的收入或利潤函數；以普通微分方程(ODE)方程的形式得出定價問題的分析解。文獻[11]研究動態定價的線性、指數和多項Logitech模型，并且提出了使用神經網絡模型以解決動態定價問題。文獻[12]建立定價政策的問題來提高在固定期限內銷售給定庫存的收入；提出Q-learning和Q(λ)算法并比較使用蒙特卡羅模擬的學習算法的性能。文獻[13]將具有隨機擾動的庫存系統被建模為連續時間隨機微分方程；綜合動態定價和生產控制，開發最大化總貼現利潤的隨機動態優化問題。文獻[14]循一階馬爾科夫隨機過程，參考效應導致最優價格路徑與預期穩態價格的單調收斂，研究近期動態定價研究趨勢，綜述多產品、競爭以及需求信息有限的問題的文獻。文獻[15]主要研究一個壟斷公司銷售一種具有無限庫存的單一類型產品的情況；在一定時間段內，產品的預期需求是隨機市場過程和取決于銷售價格的已知函數的總和。文獻[16]提出價格應該隨著時間的推移被打折，以最大化預期收益；使用動態遞歸，其中每個決策階段根據經典經濟壟斷定價理論與銷售數據估計的需求強度函數進行優化。文獻[17]提出需求的不確定性是可以通過觀察銷售情況解決的；為賣家的最優動態決策問題制定了嚴格的上限，并使用馬爾科夫決策過程(POMDP)框架來研究時尚產品賣家面臨的動態定價問題。

基于以上綜述分析得知：

(1) 這些港口企業對不同的船公司制定定價策略的文獻均是從靜態定價出發，很少考慮動態定價問題。文獻一般以操作箱量作為需求進行研究，以裝卸作業中單船裝卸作業時間作為需求的文獻不多。

(2) 目前有部分文獻已使用相關理論方法確定庫存或產品需求的動態變化帶來的影響。本文就是在此基礎上研究單船裝卸作業時間變動的需求不確定性問題。現有文獻中多數采用啟發式算法求解供應鏈中的動態定價問題，采用Q-learning算法的研究并不多。

(3) 動態定價問題的主要研究對象為供應鏈中的定價政策問題，主要有庫存問題、多產品競爭問題等，極少有關于港口動態定價問題的研究。解決動態定價的模型有線性、指數和多項Logitech模型，神經網絡模型，連續時間隨機微分方程，馬爾科夫決策過程框架等。本文研究在市場環境不穩定的前提下港口企業的動態定價問題，馬爾科夫決策過程適用于研究港口企業的動態定價問題。

因此，本文研究港口企業在應對不同的船公司提出的減少單船裝卸作業時間的要求時，以單船裝卸作業利潤最大化為目標，采用Q-learning算法求解動態定價策略的問題。Q-learning算法改善了因單船裝卸作業時間變動而導致單船裝卸作業成本變動頻繁的缺陷。

1 問題描述

港口吞吐量是衡量港口生產任務大小的主要數量指標，其中形成吞吐量的唯一來源是進出港口船舶所裝卸的貨物。裝卸貨物的時間即為單船裝卸作業時間，該時間是制定動態定價策略的重要影響因素。某船只的裝卸作業需要不同操作機械花費相應的時間進行裝卸服務。裝卸過程中調用不同的操作機械，且操作時間不同會產生相應的單船裝卸成本，從而需要合理定價以達到單船裝卸作業利潤的最大化。

單船裝卸作業時間的影響因素可以分為人為和技術影響因素。人為因素是指船公司所提出的減少單船裝卸作業時間的要求；技術因素是指單船操作箱量，不同箱型和操作箱量需要不同的操作機械花費相應時間進行裝卸作業服務。本文主要從人為因素出發，研究該因素下港口企業的動態定價問題，估計因人為因素導致的成本變動，確定單船裝卸作業時間對定價的影響。本節通過船舶裝卸作業的特點判斷單船裝卸作業時間的人為因素變動導致的成本變動原因：(1) 在船公司提出縮減單船裝卸作業時間(即希望能夠提前完成裝卸任務)的要求時，港口企業需要調動各項操作資源，直接導致成本的變動。(2) 為提高對某船只的服務效率，需要變動船舶泊位計劃，這勢必會產生額外的成本費用，若定價不變則會導致利潤減少，因此單船裝卸作業時間對定價的影響十分重要。

本文不考慮船舶泊位計劃變動產生的額外成本費用，以單船裝卸作業時間為研究對象，由成本特性及單船裝卸作業時間的重要性，確定動態定價過程如下：

(1) 對某到港船舶，確定單船操作箱量、單船裝卸作業時間與不同箱型的操作箱量。

(2) 根據歷史數據確定單船操作箱量與單箱價格、單船裝卸作業時間的函數關系。

(3) 估計船公司提出的單船裝卸作業時間變動要求所產生的預期估計誤差，使用TDABC (time-driven activity-based costing) 方法[18]，從橋吊、內集卡、堆場機械資源時的角度來衡量額外的單船變動成本，得出單船總成本函數。

(4) 計算單船總成本并得出單船裝卸利潤，使利潤最大化的定價即為最優單箱價格。

(5) 港口對同一船公司提供裝卸服務，其單船裝卸作業時間是不同的。船公司會在縮減單船裝卸作業時間方面提出相同或不同的要求，本文將以箱型為分類變量得出更加精確的價格集。

本文中，港口對同一船公司的定價做出如下假設：在單船裝卸作業時間給定的前提下，改變船公司對單船裝卸作業時間的要求，即減少單船裝卸作業時間，每一個要求會產生唯一的單箱價格集合。單箱價格與單船操作箱量和單船裝卸作業時間具有一定關聯性，為應對每個要求，選擇合適的機械資源時策略，該策略能產生唯一的最小單船變動成本。

2 模型建立

因為港口對某船公司提供的裝卸作業服務(即單船裝卸作業時間)是不同的,相同的減少要求對不同的單船裝卸作業時間的影響是不同的。所以模型中提出的所有參數均以固定的單船裝卸作業時間為基礎。

2.1 集 合

箱量類型集合I,I={1,2,…,n}，機械類型集合J，J={1,2,…,m}。

2.2 參 數

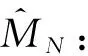
T(P,S):單箱價格為P、單船操作箱量為S和單船裝卸作業時間T的函數關系式，由歷史定價數據結合logit模型確定。

C:單船裝卸總成本。

C1:單船裝卸固定成本。

C2:船公司提出的減少單船裝卸作業時間所產生的單船變動成本。

Tij:箱型i使用機械j進行操作時的單位作業耗用資源時(產能)，i∈I,j∈J。

cj:機械j的單位作業產能成本，即各操作機械類型：內集卡、吊橋、堆場作業時產生的單位作業成本，j∈I。

sj:機械j的操作箱量，即作業動因量，j∈J。

si:不同箱型i對應的箱量，i∈I。

Tcz:船公司提出需要減少的單船裝卸作業時間。

m:單船變動成本可以增加的最大值。

2.3 決策變量

xij:表示是否選擇改變箱型i所需機械j的資源時(產能)，i∈I,j∈J。

pi:港口對船公司提出的箱型i的單箱價格，根據港口對不同船公司的歷史定價數據確定價格的上下限，pi∈[pl,ph],i∈I；pl、ph分別價格上、下限；0≤pl≤ph≤∞。

2.4 數學模型(DP)

(1)

約束條件：

pl≤pi≤ph?i∈I

(2)

?t∈N

(3)

?t∈N

(4)

目標函數式(1)表示不同箱型的價格為p={p1,…,pi,…,pn}，與對應箱量為s={s1,…,si,…,sn}時的期望單船裝卸利潤最大化。單船裝卸總成本C由單船固定成本C1和單船變動成本C2構成:

C=C1+C2

(5)

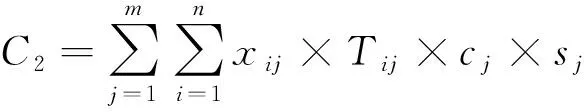
t∈N

(6)

式中：Ti(Pi,Si)是指得知歷史單箱價格為Pi，箱量為Si時得到的單船裝卸作業時間為Ti；T(P,S)是由歷史數據集合：單船裝卸作業時間集合DT(T1,…,Ti,…,Tn)， 單船的單箱價格集合DP(P1,…,Pi,…,Pn)和單船操作箱量集合DS(S1,…,Si,…,Sn)結合logit模型得出：

(7)

式中：b1、b2分別為歷史單箱價格和歷史單船箱量對于單船歷史裝卸作業時間的預期估計誤差，B為客戶基數。

因歷史數據中未有明確的不同箱型的單箱價格，本文使用pt表示在t時刻所有箱型的平均單箱價格。將pt代入歷史數據集合DP中尋找對應的P，并從集合DS得出相對應的S；將P和S代入式(7)求解得到t時刻對應的單船裝卸作業時間T。

(8)

Ti(Pi,Si)為根據歷史數據Pi、Si得出的單船裝卸作業時間Ti，T(P,S)為由歷史數據集合結合logit模型擬定的函數關系表達式。

3 基于Q-learning算法的港口動態定價策略

3.1 港口對于船公司制定的動態定價策略

Q-learning算法[12]是求解馬爾科夫鏈(MDP)的值迭代方法，選擇合適的動作狀態對并在t時刻得出每一個狀態state(s)采取某動作action(a)的反饋reward(r)；定義Q(s,a)表示每個狀態s所對應a的效用值矩陣，更新Q矩陣：

Q(st,at)=Q(st,at)+α×(r+γ×

max(Q(st+1,a))-Q(st,at))

(9)

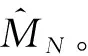
初始化：N、b1、b2、B、si、Tcz、單船操作箱量所確定的單船裝卸作業時間T、探索率ε、折扣因子γ、學習速率α。

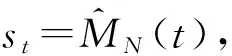
使用ε判定a是探索或學習，若a需要學習則利用目前Q矩陣中最大值Q所對應的a，否則在A中隨機選擇不同箱型的單箱價格作為a。狀態值為s時采取動作a后得到下一個狀態值，即s′。使用MATLAB調用yalmip工具箱計算0-1整數規劃得到xij及其產生的單船變動成本C1，得到立即回報值r。

用式(9)迭代更新Q矩陣，在迭代終止時選擇Q矩陣中的最優Q值得到s和a，即單船不同箱型的最優單箱價格。

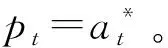
最優Q矩陣中選定的a為港口企業在應對不同的船公司提出不同單船裝卸作業時間的情況下，為達到裝卸作業利潤最大化的目標所制定的動態價格。

要注意的是，港口對同一船公司提供裝卸服務，其單船裝卸作業時間是不同的。最優單箱價格是指在固定單船裝卸作業時間的前提下得到的不同箱型的價格集合。對某一單船裝卸作業時間來說，改變Tcz得出的最優單箱價格集合是該單船裝卸作業時間的動態定價表。港口對同一船公司的動態定價策略是由不同單船裝卸作業時間的動態定價表構成的。

3.2 約束條件限制策略

算法1港口動態定價的Q-learning算法

初始化：

k=1,s=1,Q(s,a)=0，其中，s∈S,a∈A

設定ε、γ、α，大迭代次數κ

對于所有k≤K

Step1：狀態s,使用ε-greedy策略選擇利用或探索a

Step2：狀態s下采取動作a，式(1)得到立即回報值r，式(8)得到下一狀態s′

Step3：

Q(st,at)=Q(st,at)+α×(r+γ×max(Q(st+1,a))-Q(st,at))，s←s′

Step4：重復Step2、Step3；直到s′=max(s)時停止

約束限制策略如下：

1) 式(2)限定a∈A(s)，設定:

s={0,0.1,0.2,…,30}

2) 式(3)求解結果精確度在±0.01小時；式(4)最大成本值為5萬元。

3) 已知s、s′、r；若r<0，令s′=s；否則由式(9)更新Q矩陣。

4)Q(s,a)矩陣維度大，規定s和a為單精度；為使得式(4)求解精確，計算s′時采用雙精度，輸出s′結果時調整為單精度。由精度引起的變動會導致一定程度上選取s所在id困難，規定若無法正確選取s的id，令s′=s。

4 案例分析

4.1 定價策略的細分及參數確定

為確保動態定價策略符合實際需求，以2016年上海港對船公司1的歷史定價數據作為主要參考，并輔以其余3大船公司的歷史定價信息，確定單船裝卸作業時間和單船操作箱量的分界線。歷史定價信息中并未有明確的不同箱型的單箱價格，僅以單船裝卸總利潤除以總箱量得出單船的單箱價格。式(2)的上下限如圖1所示。結果表明：單船操作箱量分界點為2 000 TEU、單船裝卸作業時間分界點為20小時；確定單船裝卸作業時間的上、下限分別為10小時和40小時；上海港對船公司1、2、3、4制定的單箱價格下限分別為700元/TEU、300元/TEU、550元/TEU，510元/TEU，上限設置為1 000元/TEU。同時引入箱型因素，使得定價策略更為精確。基于上海港對船公司1的歷史數據如表1所示。使用1stopt軟件估計式(7)中的參數：b1=0.000 1，b2=0.728，B=1 653.4。使用2016年12個月的產能成本數據計算得出各操作機械的產能成本率，如表2所示。

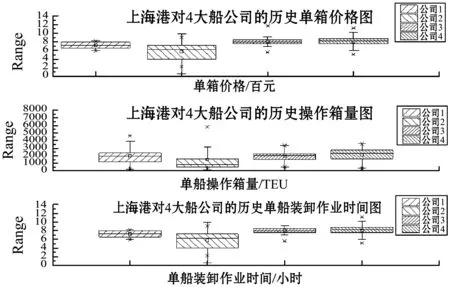
圖1 上海港對4大船公司的歷史單箱價格、單船操作箱量、 單船裝卸作業時間的箱線圖

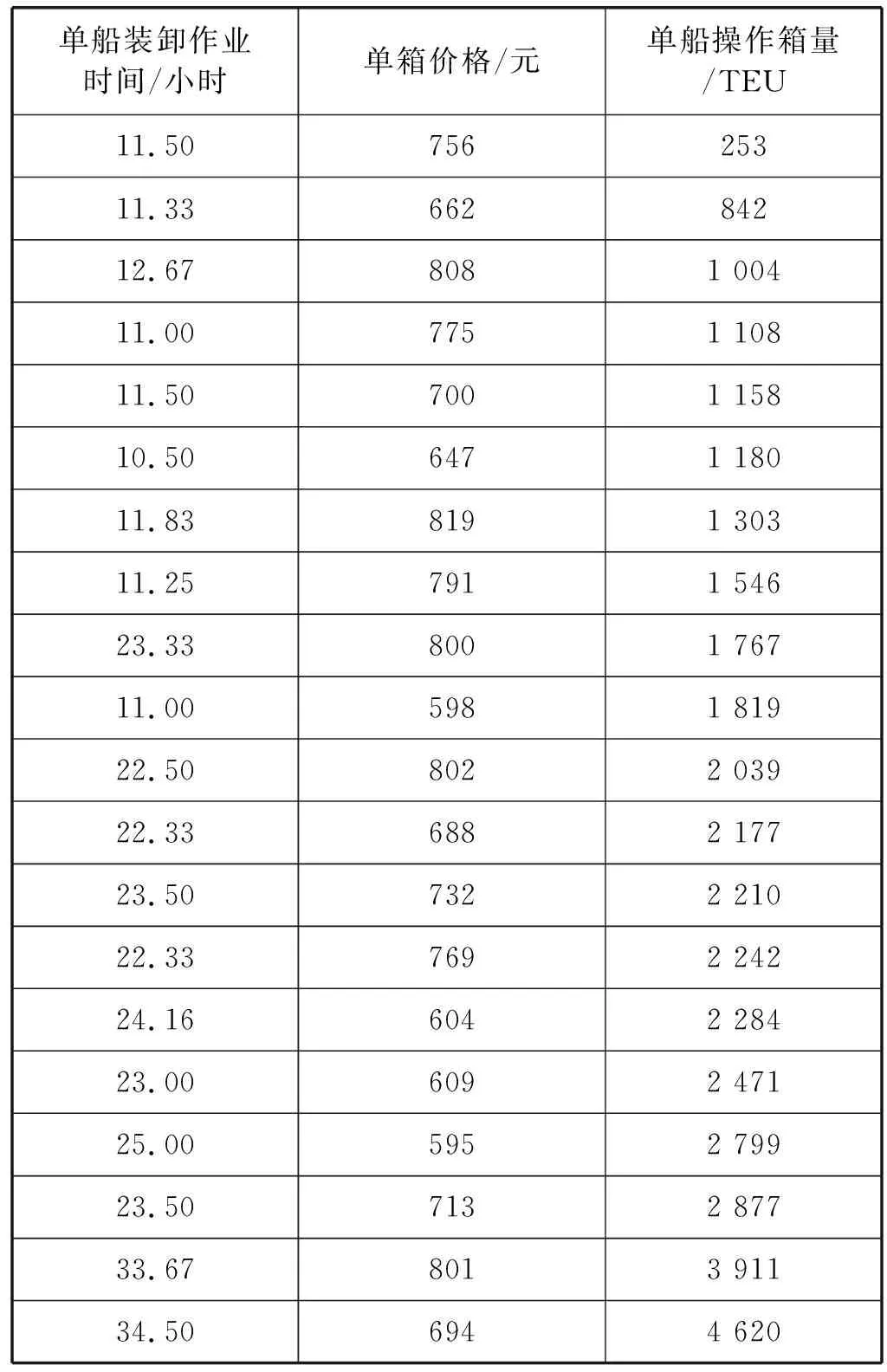
單船裝卸作業時間/小時單箱價格/元單船操作箱量/TEU11.5075625311.3366284212.678081 00411.007751 10811.507001 15810.506471 18011.838191 30311.257911 54623.338001 76711.005981 81922.508022 03922.336882 17723.507322 21022.337692 24224.166042 28423.006092 47125.005952 79923.507132 87733.678013 91134.506944 620

表2 各機械產能成本率產能

4.2 算法參數與單船裝卸利潤的分析

動態定價策略是根據不同的船公司對港口企業提出的減少單船裝卸作業時間Tcz的要求制定的，不同的單船裝卸作業時間在不同的Tcz變動影響下均能夠產生相應的價格集。Tcz的變動會導致單船裝卸成本變動，從而影響單船裝卸利潤，本節將使用單船裝卸利潤作為衡量指標。為了能夠明確感受使用Q-learning算法制定的動態定價策略對于單船裝卸利潤的影響，本節從是否連續減少單船裝卸作業時間進行舉例說明。

首先，設定單船裝卸作業時間Tcz均減少1小時，取滑動窗口N=21，根據4.1節中求解得出的參數，以上海港對四大船公司的歷史單船裝卸作業時間為主要依據，使用Q-leaning算法求解得出不同的最優單箱價格集合。因同一船公司在不同月份會有不同的單船裝卸作業時間，即在1～12月份均由相對應的定價表，所得定價表的數據量過大，本文將12個月份劃分成了四季。定價表將從單船裝卸作業時間、單船操作箱量和季節三個方面綜合得出上海港對四大船公司的定價表，如表3所示。相同月份中只要單船裝卸作業時間不同，則會產生唯一最優價格。同時，不同月份中單船裝卸作業時間相同或者不同時也有對應的唯一價格。因將12個月份劃分成了四季，在表中顯示的最優價格結合了季節中三個月的價格形成了最優價格區間。結果表明：上海港對不同公司在相同箱型下的定價策略受到單船裝卸作業時間和單船操作箱量的影響。以公司1為例，當單船裝卸作業時間小于20小時并變動至20小時以上的情況下，FR、RF的變動不明顯，約在800～1 000元/TEU；GP、HC、OT和TK 在單船裝卸作業時間小于或者大于20小時的情況下，隨月份的增加價格趨勢變動劇烈。從整體定價來看，除6月份外，定價隨單船裝卸作業時間的增長呈上升趨勢，且在8到12月份間差距明顯。單船裝卸作業時間小于20小時的情況下，公司1-公司3的單船操作箱量均2 000 TEU以下；公司4則幾乎沒有單船裝卸作業時間低于20小時的情況出現。上海港對不同的船公司定價時需要充分考慮船公司單船操作箱量和單船裝卸作業時間，充分應對船公司提出的減少單船裝卸作業時間的要求并制定合理以及詳細的價格表。

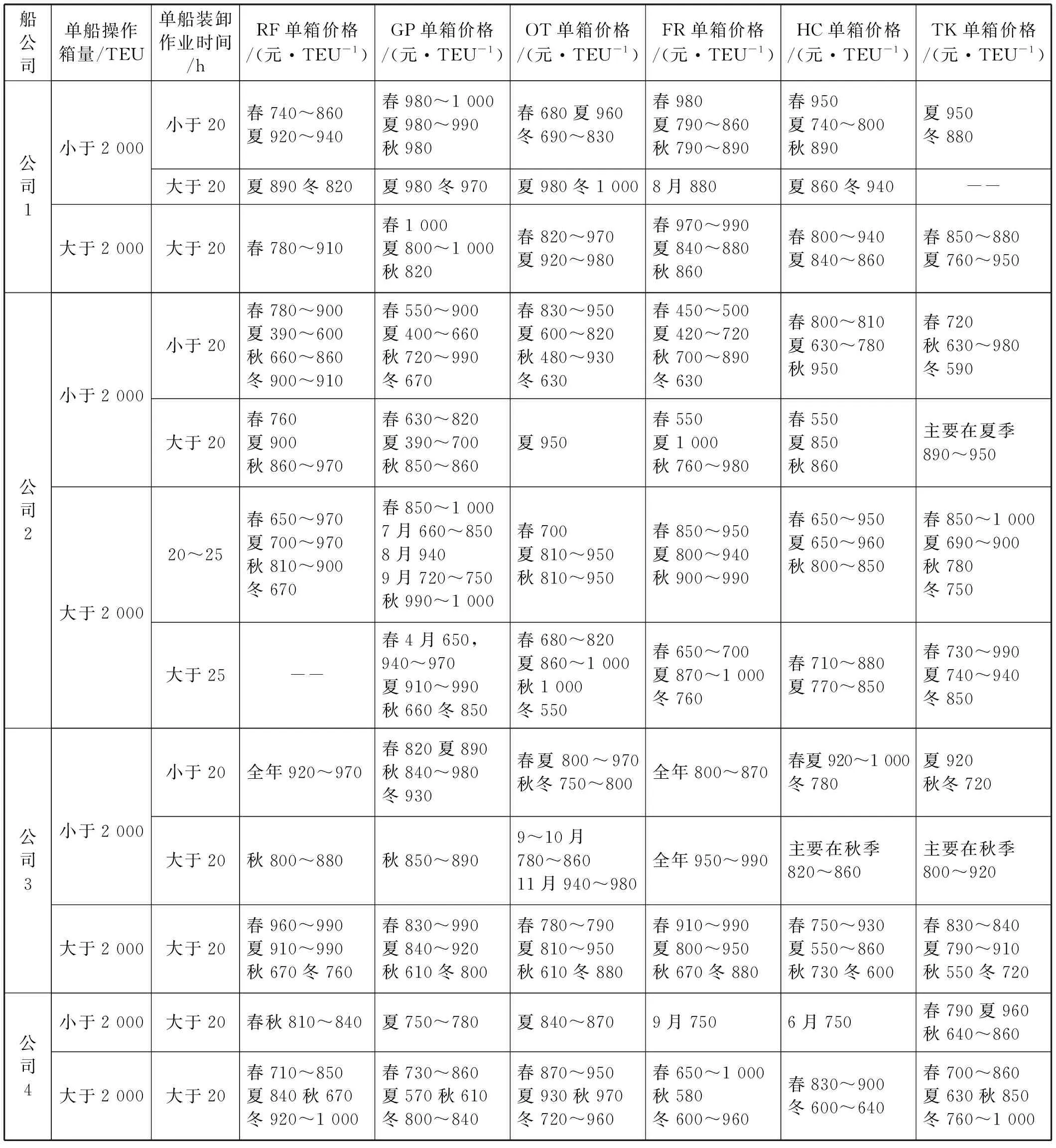
表3 上海港對于4大船公司的定價表

其次，以上海港對船公司1的動態定價策略為例，本節從兩方面舉例說明動態定價策略如何應用于實際以及使用Q-leaning算法求解后其參數對于單船裝卸利潤的影響。(1) 船公司1要求減少的單船裝卸作業時間不變，改變Q-learning算法中的參數。以折扣因子為例，隨單船裝卸作業時間的增長，折扣因子對單船裝卸利潤的影響如圖2所示。結果表明：隨單船裝卸作業時間增長，單船裝卸利潤呈現單調上升趨勢。折扣因子從0.1變動至0.7時，單船裝卸利潤增至352.77萬元，0.7至0.9時降至159.89萬元。(2) 船公司1要求減少的單船裝卸作業時間發生變動，而Q-learning算法中的參數不變。以學習速率為例，船公司1要求單船裝卸作業時間減少0.3、0.6、0.9、1.2和1.5小時，即={0.3,0.6,0.9,1.2,1.5}。學習速率對單船裝卸利潤的影響如圖3所示。結果表明：根據單船裝卸作業時間的減少情況，單船裝卸利潤隨著學習速率的增加呈先增后減的趨勢。例如單船裝卸作業時間減少0.3小時的情況下，學習速率為0.3時單船裝卸利潤達到106.16萬元；學習速率為0.9時單船裝卸利潤降至106.09萬元。相同學習率，單船裝卸作業時間由10.5小時減少至9小時的情況下，單船裝卸利潤波動明顯。例如學習速率為0.7時，單船裝卸作業時間為9.9小時，單船裝卸利潤達到最小值為105.90萬元；單船裝卸作業時間為9.6小時單船裝卸利潤達到最大值為106.14萬元。因此，Tc2的變動和Q-learning算法中參數的變動對于單船裝卸利潤有顯著的影響。

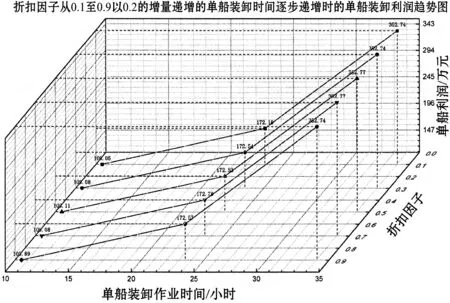
圖2 以折扣因子為分類的裝卸時間遞增時的 單船利潤趨勢圖

圖3 單船裝卸作業時間逐漸減少時的學習速率從0.1 至0.9以0.2的增量遞增的單船利潤趨勢圖

5 結 語

本文運用Q-learning算法求解得出港口企業對不同的船公司所制定的動態定價策略，得出以下結論：

(1) 學習速率越大，保留之前經驗的效果越少；折扣因子γ越大，Q(s，a)作用越大。同時學習速率對于單船裝卸利潤的影響大于折扣因子，但是過大的學習速率、折扣因子會導致動作a被以往經驗所限制，利潤值陷入局部最優；過大的探索率會導致a過于自由探索，易忽略以往最優經驗。在實際應用中，可以將今年的實際數據作為最終需要求解得到定價策略的依據，使用前幾年的數據代入模型算法中求解得出合適的折扣因子和學習速率，并分析選擇相應的折扣因子和學習速率作為已知條件，最后使用今年的實際數據得出相應決策。

(2) 上海港實際數據分析表明，對同一船公司在相同箱型下的定價策略亦受到單船裝卸作業時間的影響。上海港對不同的船公司定價時，需要充分考慮該公司通常所需的單船操作箱量及單船裝卸作業時間，制定合理以及詳細的定價策略。本文所提出的基于Q-learning算法的動態定價策略可以有效提高港口企業的競爭力，能夠及時有效地應對船公司提出的不同需求并得出相應的動態定價策略，促進港口經濟的發展。從案例結果可以看出，單船裝卸作業時間對單船裝卸利潤具有很大的影響。為提高單船裝卸利潤，港口可以從單船裝卸作業時間著手，提高單船裝卸效率，減少單船裝卸成本。因單船裝卸作業時間與港口裝卸設備等一系列基礎設施有關。為實現高效的單船裝卸效率，港口可通過數字化、自動化技術，提升碼頭作業運作能力，改善港口信息不透明狀況，提升對單船裝卸作業流程的設備、人員等資源充分使用、檢測、維修的能力。