考慮多類別危險品的危險品多式聯(lián)運選址及路徑規(guī)劃

趙志文 楊 斌 朱小林

(上海海事大學物流科學與工程研究院 上海 201306)

0 引 言

危險品多式聯(lián)運是指通過使用多種交通方式將危險品從起點運輸?shù)浇K點的過程。在有限的區(qū)域內(nèi)，考慮到轉(zhuǎn)運過程會增加整個運輸環(huán)節(jié)的成本、風險和時間，危險品通常只由一種方式運輸。但是在不同區(qū)域之間的運輸，由于運輸距離較遠和運輸規(guī)模的增加，多式聯(lián)運被廣泛地使用著。這使得運輸商既能夠受益于短途卡車運輸?shù)撵`活性又可以享受長途鐵路運輸或者水路運輸?shù)囊?guī)模經(jīng)濟優(yōu)勢[1]。

世界交通運輸網(wǎng)絡日常轉(zhuǎn)運約40億噸的危險貨物[2]，運輸過程中危險品意外泄漏的風險受到社會和政府的極大關注。在危險品存儲、運輸過程中對危險品不采取安全有效的管理措施的話，事故將會對個人生命財產(chǎn)安全和環(huán)境構成巨大的潛在威脅，所以有必要設計可靠的危險品運輸網(wǎng)絡來安全管理危險品運輸。

危險品選址和運輸路線選擇問題(Location-Routing Problems)是選址問題(Location-Allocation Problems)和車輛路徑選擇問題(Vehicle Routing Problems)的集成問題。由于危險品運輸?shù)奶厥庑砸约斑@兩類NP難題的集成使得國內(nèi)外對危險品選址和路線選擇問題的研究相對較少。Current等[3]作為這一領域的先驅(qū)者之一首先建立了同時考慮危險品設施選址以及路徑的多目標整數(shù)規(guī)劃模型。基于此，Cappanera等[4]針對危險品選址和路徑問題建立了一個單目標模型，并提出了拉格朗日松弛算法和分支定界算法來解決它。帥斌等[5]利用改進的蟻群算法對危險品LRP問題進行了求解，并通過算例驗證了模型和算法的有效性。喬聯(lián)寶等[6]根據(jù)成本、選址風險、暴露人口數(shù)量以及危險事件發(fā)生概率最小化為目標,建立了無時間約束條件下的危險品LRP模型。但前面這些大部分只是考慮了單一的運輸方式，并沒有考慮在實際運輸過程中會出現(xiàn)多種運輸方式的情況。

國內(nèi)外對危險品多式聯(lián)運運輸方面問題的研究較少。XIE等[7]首次探討危險貨物公鐵路的選址—路徑問題，構建一個以成本和風險加權值最小為目標的混合整數(shù)線性規(guī)劃模型。Ghazal等[8]考慮了危險品運輸在轉(zhuǎn)運中心的擁堵問題以此構建了一個非線性MIP問題，并使用遺傳算法求解證明了模型的有效性。開研霞等[9]比較了不同的運輸方式及路徑下的事故損失和運輸成本，得到了多式聯(lián)運在一定程度上可以降低危險品運輸過程中的社會總期望損失和運輸成本的結論。辛春林等[10]用Dijkstra改進算法和O-D矩陣搜索算法求解所建模型。付曉鳳等[11]通過根據(jù)多式聯(lián)運運輸方式危險性排序、環(huán)境危險性評估、貨物固有的危險特性判斷、聯(lián)運系統(tǒng)的危險性等確定危險品運輸系統(tǒng)危險性。Leonelli等[12]將基于運輸風險和運輸成本的選線問題轉(zhuǎn)化為“最小費用流”問題,依據(jù)圖論-網(wǎng)絡理論進行選線優(yōu)化。

以上文獻多只是研究單一的運輸方式以及單一的危險品類型，并沒有考慮多式聯(lián)運的運輸方式以及多類別危險品在運輸過程中的相互影響。而在危險品運輸?shù)倪^程中，使用最為常見的運輸方式為公-鐵運輸。本文在公鐵聯(lián)運前提下，通過描述不同危險等級危險品之間的相互影響，綜合考慮了危險品多式聯(lián)運選址及最優(yōu)路徑，建立了一個雙目標0-1整數(shù)規(guī)劃模型來同時優(yōu)化危險品運輸過程中的風險問題以及運輸成本問題。

本文的創(chuàng)新點：

1) 考慮了在危險品運輸過程中的公鐵聯(lián)運的運輸方法，并根據(jù)其運輸特點構建了一個約束于風險與成本的雙目標模型，且模擬的算例可以使用Lingo及Cplex軟件快速求解。

2) 考慮了危險品在轉(zhuǎn)運中心的轉(zhuǎn)運特點，提出了一個優(yōu)先排隊的規(guī)則來模擬多類別危險品在中轉(zhuǎn)節(jié)點服務的過程。

3) 在模型中引入經(jīng)濟轉(zhuǎn)化因子，將風險轉(zhuǎn)化為經(jīng)濟指標，將雙目標轉(zhuǎn)化為單目標問題。

1 模型建立

1.1 問題描述

給定一個人口密集的網(wǎng)絡，包含運輸節(jié)點和節(jié)點之間的弧。運輸節(jié)點包括普通的運輸節(jié)點和候選的轉(zhuǎn)運樞紐點。候選的轉(zhuǎn)運樞紐點如果被確認為轉(zhuǎn)運點，那么在該點就可以進行每一批貨物的轉(zhuǎn)運操作。因本文只考慮公鐵聯(lián)運的情況，網(wǎng)絡中的弧包括2種運輸方式(公路運輸，鐵路運輸)。網(wǎng)絡中存在一系列的O-D對(配送任務)，每個節(jié)點都可以作為運輸任務的起點或終點。

危險品的運輸與普通貨物的運輸不同。當其在不同的運輸方式中變換時，通常需要一些專業(yè)的設備以及受過專業(yè)培訓的操作者。貨運公司在設計運輸網(wǎng)絡時由于成本和預算的原因，將所有候選轉(zhuǎn)運節(jié)點都投資為正式的轉(zhuǎn)運場往往是不現(xiàn)實的。此外，這些轉(zhuǎn)運樞紐點的選擇會影響著每個配送任務的最佳路徑和網(wǎng)絡的總運輸風險。考慮到這些因素，本文同時考慮了轉(zhuǎn)運樞紐點的選址以及配送任務的最佳路徑。

在運輸網(wǎng)絡中考慮了多種危險品。本文的目標為通過選擇最佳的轉(zhuǎn)運節(jié)點和每組危險品的最佳路徑來最小化成本以及減少總體運輸風險。隨著危險品在轉(zhuǎn)運節(jié)點時花費時間的增加，危險品的風險會增加。為了模擬這個問題，使模型更具現(xiàn)實意義，本文提出了一個優(yōu)先排隊的規(guī)則來模擬危險品在中轉(zhuǎn)節(jié)點服務的過程。每個訂單都會根據(jù)危險的等級來排序，并要求在中轉(zhuǎn)點優(yōu)先處理高優(yōu)先級的危險品。

1.2 假設前提

(1) 每個訂單的訂單屬性是已知的，且每條路徑和每個轉(zhuǎn)運節(jié)點上有容量限制。

(2) 每個候選轉(zhuǎn)運節(jié)點有轉(zhuǎn)運危險品的等級限制。

(3) 每個訂單只能走一條路徑(弧)一次。

(4) 只考慮兩種運輸方式，即公路和鐵路。

(5) 候選的轉(zhuǎn)運中心只有被確定為轉(zhuǎn)運節(jié)點才可以在該點發(fā)生進行運輸方式轉(zhuǎn)變。

1.3 參數(shù)變量

c以危險等級排序的配送任務

lcc配送任務的配送量

fii候選節(jié)點的固定成本

ki1,i2在(i1,i2)弧上運輸?shù)膯挝怀杀?/p>

ti在轉(zhuǎn)運節(jié)點i轉(zhuǎn)運的單位成本

ri1,i2在弧(i1,i2)運輸?shù)膯挝伙L險

ri在轉(zhuǎn)運節(jié)點i轉(zhuǎn)運的單位風險

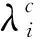
Ri轉(zhuǎn)運節(jié)點i能服務危險品的最大等級

Pi在轉(zhuǎn)運節(jié)點i能夠轉(zhuǎn)運的總?cè)萘?/p>

Pi,j在弧(i,j)運輸?shù)目側(cè)萘?/p>

Yi若在候選節(jié)點i建立轉(zhuǎn)運中心為1，否則為0

1.4 轉(zhuǎn)運節(jié)點的轉(zhuǎn)運時間求解

在運輸中危險品往往集中在轉(zhuǎn)運樞紐點以接收服務并轉(zhuǎn)移到其他節(jié)點。轉(zhuǎn)運樞紐點的容量是有限的，所以往往導致運輸?shù)膿矶潞脱诱`，從而增加風險。本文考慮危險貨物運輸時基于危險度優(yōu)先，以模擬在轉(zhuǎn)運節(jié)點的危險貨物的流量。

假設這個排隊系統(tǒng)中的中心節(jié)點有多個服務器和無限隊列，這使得可將由危險貨物運輸形成的隊列建模為M/M/V排隊系統(tǒng)。在本文系統(tǒng)下，轉(zhuǎn)運中心會根據(jù)危險品的編號來優(yōu)先處理危險等級高的貨物。也就是說，c=1的危險度具有最高優(yōu)先級，優(yōu)先級按升序的方式依次降低。

根據(jù)上面的描述和理論[13],得到如下公式：

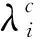
(1)

(2)

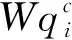
?c∈C,i∈NHR

(3)

(4)

(5)

(6)

2 雙目標整數(shù)規(guī)劃模型

根據(jù)問題描述，建立基于多類別危險品的多式聯(lián)運雙目標整數(shù)規(guī)劃模型：

(7)

(8)

minTotal=αC+(1-α)βR

(9)

(10)

(13)

M(1-Yi) ?i∈NHR,c∈C

(14)

(15)

(16)

(17)

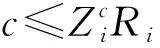
(18)

Yj∈{0,1} ?i∈NHR

(19)

(20)

(21)

3 實例計算

3.1 基本數(shù)據(jù)

本文以一個模擬的運輸網(wǎng)絡為例進行算例求解。此運輸網(wǎng)絡中有著13個運輸節(jié)點(A-M)，其中有7個普通的運輸節(jié)點，6個作為候選轉(zhuǎn)運的節(jié)點。在整個網(wǎng)絡中存在著公路和鐵路兩種運輸方式，如圖1所示。

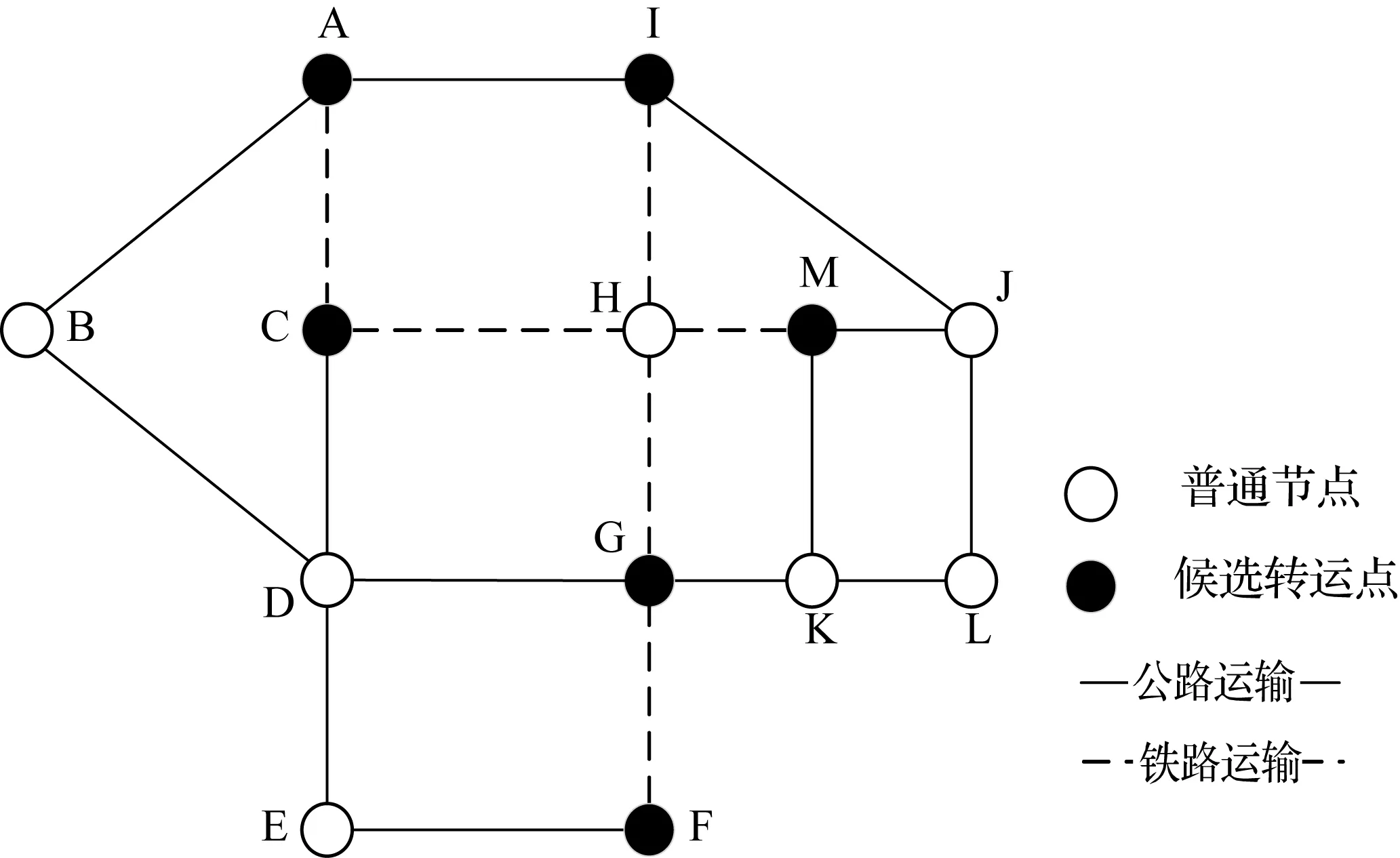
圖1 運輸網(wǎng)絡

候選節(jié)點包括A、C、F、G、I、M。每個候選節(jié)點的建造成本、容量、風險、轉(zhuǎn)運單位成本、服務率參見表1。每條弧上的單位運費、容量以及風險如表2所示。各訂單貨物的危險等級以及需求量見表3(假設α=0.5,β=2)[10]。由于缺乏真實數(shù)據(jù)，表中為模擬數(shù)據(jù)。

表1 候選轉(zhuǎn)運節(jié)點屬性

表2 每條路經(jīng)的屬性

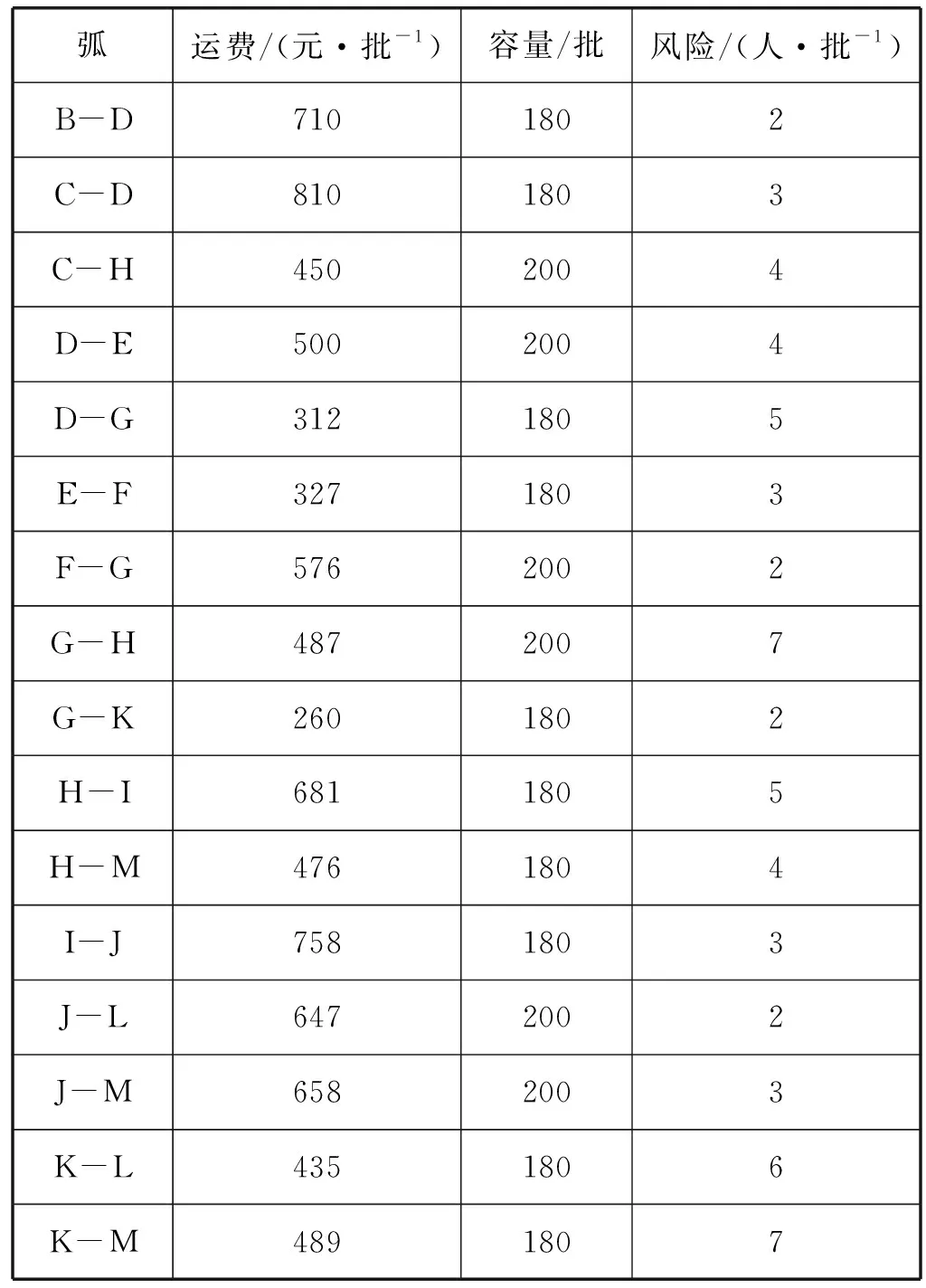
續(xù)表2

表3 各訂單貨物的屬性

使用lingo軟件對模型進行求解，得到唯一最優(yōu)解，計算結果如表4所示。在α=0.5、β=2的條件下，在6個候選轉(zhuǎn)運點中選C、M、G三點。運輸總成本為3 345 494元，危險品運輸對周圍居民造成影響的社會成本為18 235元。

表4 訂單路徑及轉(zhuǎn)運點選擇

3.2 計算結果分析

在此基礎上，改變α的取值，進行參數(shù)分析。如表5和圖2所示，α取值從0.1到0.9的過程中，每一行都代表著一個最優(yōu)的解。可以看到，當運輸成本的比重逐漸增加的同時，運輸活動對周圍居民造成的影響會越大。根據(jù)圖2顯示，在此條件下，當選擇α小于0.2時會導致總成本非常高，風險在接受能力之內(nèi)。同樣的，當選擇α大于0.7時會使總風險非常高，相應的總成本會降低。這些能夠在一定程度上幫助決策者進行決策。

表5 參數(shù)分析

圖2 總成本關于總風險的函數(shù)

決策者如果對運輸成本的重視程度和風險的重視程度之間的關系沒有確切的掌握的話，那么他最好選擇3～8號，一旦超出這個范圍成本和風險都會有劇烈的變動。若決策者對于成本控制的要求非常高，而對風險的要求并不高那么可以選擇α大于0.7的選址與路徑規(guī)劃策略。相反,若決策者對于風險控制的要求非常高，而對運輸成本的要求并不高那么可以選擇α小于0.2的選址與路徑規(guī)劃策略。

4 結 語

(1) 基于運輸方式的多樣性，以及貨物類別的多樣性，以成本最小以及危險品暴露危險最小為目標，構造了多式聯(lián)運路徑規(guī)劃模型。并成功求解相關案例，證明了模型的有效性。在轉(zhuǎn)運過程中有一些其他影響因素，如政治因素、天氣因素、人為因素等，也會對作業(yè)起很大影響，下一步考慮將這些因素考慮到模型中。

(2) 模型中引入經(jīng)濟轉(zhuǎn)化因子，將風險轉(zhuǎn)化為經(jīng)濟指標，避免各目標單位不統(tǒng)一的問題。經(jīng)濟轉(zhuǎn)化因子的值的變化會對結果有著非常大的影響，但由于缺乏足夠的信息，本文經(jīng)濟轉(zhuǎn)化因子的值無法準確地確定。對于現(xiàn)實中的危險品運輸?shù)膽茫僭O的β的值可以更合理地進行調(diào)整。

(3) 在現(xiàn)實生活中，對于小規(guī)模的危險品物流網(wǎng)絡可以用Lingo、CPLEX求解，但對于大規(guī)模的復雜網(wǎng)絡來說，此方法不能有效快速求解。下一步將考慮設計智能算法來求解此類問題。