凹版印刷基材烘干溫度對張力的影響機(jī)理分析
何奎,陶濤,劉善慧
(1.西安交通大學(xué)機(jī)械工程學(xué)院,710049,西安;2.西安理工大學(xué)印刷包裝與數(shù)字媒體學(xué)院,710048,西安;3.河南科技大學(xué)機(jī)電工程學(xué)院,471003,河南洛陽)
社會(huì)發(fā)展對印刷品的質(zhì)量要求越來越高,同時(shí),電子軸技術(shù)的發(fā)展為印刷質(zhì)量的提高提供了基礎(chǔ)。凹版印刷是一種重要的印刷工藝,以其優(yōu)秀的印刷品質(zhì)而廣泛應(yīng)用。凹版印刷基材即印刷行業(yè)俗稱的承印物料帶。在電子軸凹版印刷中,料帶張力控制精度是一個(gè)重要的技術(shù)指標(biāo),是印刷質(zhì)量的基礎(chǔ)。為了提高張力控制精度,需要對張力系統(tǒng)模型進(jìn)行深入的研究。
電子軸凹版印刷的張力系統(tǒng)主要分為3個(gè)部分:放卷、印刷和收卷。不同部分對料帶張力有不同的要求,很多學(xué)者把研究重點(diǎn)放在放卷和收卷部分。在這些研究中,首先建立放卷或收卷的張力模型,然后采用不同控制算法控制料帶張力。Li等針對放卷系統(tǒng)分別設(shè)計(jì)了基于神經(jīng)元網(wǎng)絡(luò)的張力控制器和H∞魯棒控制器[1-2]。Liu等采用自抗擾解耦控制算法控制放卷系統(tǒng)張力[3-4]。Gassmann等在料帶處理系統(tǒng)的放卷部分中采用了固定階H∞張力控制算法[5]。Yang等為料帶張力控制系統(tǒng)設(shè)計(jì)了模糊自適應(yīng)PID控制器[6]。Park在收卷系統(tǒng)張力控制中也采用了自適應(yīng)增益PID控制方法[7]。Abjadi等在料帶收卷系統(tǒng)中采用滑模控制方法控制收卷張力[8]。尹周平課題組對放卷部分的非連續(xù)開卷張力控制進(jìn)行研究[9]。張永芳等在凹版印刷機(jī)放卷張力控制中采用了模糊自抗擾控制方法[10]。Wu課題組對放卷張力系統(tǒng)的建模方法進(jìn)行了研究[11]。這些研究較好地解決了放卷和收卷部分的張力穩(wěn)定性問題,使得印刷部分的張力穩(wěn)定性也得到了一定的提高,但印刷部分的張力還與版輥運(yùn)動(dòng)等因素有關(guān),印刷部分張力穩(wěn)定性問題沒有得到根本解決。
在印刷部分,張力系統(tǒng)和套準(zhǔn)系統(tǒng)耦合在一起。一些學(xué)者對套準(zhǔn)模型及其控制算法進(jìn)行研究,但主要都是基于傳統(tǒng)的R2R(Roll-to-Roll)張力模型,并沒有考慮凹版印刷工藝中的一個(gè)極其重要的環(huán)節(jié)即烘干。Martz等對印刷部分的基材進(jìn)行了有限元建模,以便于進(jìn)一步實(shí)現(xiàn)解耦控制[12-13]。Tran等采用回推控制方法對多跨度料帶傳動(dòng)系統(tǒng)進(jìn)行控制[14]。Chen等印刷套準(zhǔn)控制中采用了優(yōu)化的前饋PD解耦控制方法[15-16]。Liu等針對印刷部分進(jìn)行了套準(zhǔn)建模和前饋?zhàn)钥箶_控制器設(shè)計(jì)[17-18]。劉成等對印刷部分的同步控制進(jìn)行了研究[19]。
在電子軸凹版印刷設(shè)備的印刷部分,每一個(gè)印刷單元后面都設(shè)有烘箱,用于烘干料帶上的油墨。烘箱內(nèi)部的料帶溫度遠(yuǎn)高于烘箱外部的料帶溫度。料帶材料為雙向拉伸聚丙烯(BOPP)塑料薄膜時(shí),烘干溫度一般在60~80 ℃。烘箱外部溫度,即生產(chǎn)車間的室溫,一般在20 ℃左右。干燥系統(tǒng)會(huì)對料帶張力特性產(chǎn)生影響,進(jìn)而影響張力控制精度。塑料薄膜材料對溫度比較敏感,受溫度的影響主要體現(xiàn)在兩個(gè)方面:楊氏彈性模量和熱膨脹系數(shù)。實(shí)際上,烘干溫度對張力系統(tǒng)和套準(zhǔn)系統(tǒng)的影響是非常顯著的,已經(jīng)開始引起一部分學(xué)者的注意。Pagilla團(tuán)隊(duì)建立了數(shù)學(xué)模型用于確定運(yùn)動(dòng)料的溫度分布狀態(tài)[20-21],但缺乏干燥系統(tǒng)對張力影響的相關(guān)研究。He等在印刷張力建模中開始考慮干燥系統(tǒng),但未分析干燥系統(tǒng)對基材張力的影響[22]。
目前,在電子軸凹版印刷系統(tǒng)中,仍然缺乏干燥系統(tǒng)對印刷部分料帶張力影響的相關(guān)研究。隨著印刷質(zhì)量要求的提高,烘干溫度對張力的影響將無法忽視。因此,本文首先建立了包含干燥系統(tǒng)的印刷部分張力模型,然后通過模型仿真分析烘干溫度對張力的影響規(guī)律。
1 包含烘干的印刷系統(tǒng)張力建模
圖1所示為電子軸傳動(dòng)凹版印刷機(jī)系統(tǒng)組成示意圖,主要分3部分:放卷、印刷和收卷。放卷部分采用兩段張力結(jié)構(gòu),分別設(shè)置一個(gè)擺輥機(jī)構(gòu)和張力傳感器,擺輥機(jī)構(gòu)用于抑制張力波動(dòng)并測量料帶張力,張力傳感器僅用于測量料帶張力。收卷部分與放卷部分類似。多色印刷部分的每一個(gè)料帶區(qū)間設(shè)置一個(gè)張力傳感器,用于測量料帶張力。從第2色印刷單元開始,每個(gè)印刷單元后設(shè)置一個(gè)光電眼,用于檢測套準(zhǔn)誤差。在每一色印刷單元之后設(shè)置一個(gè)烘箱,用于烘干印刷油墨。
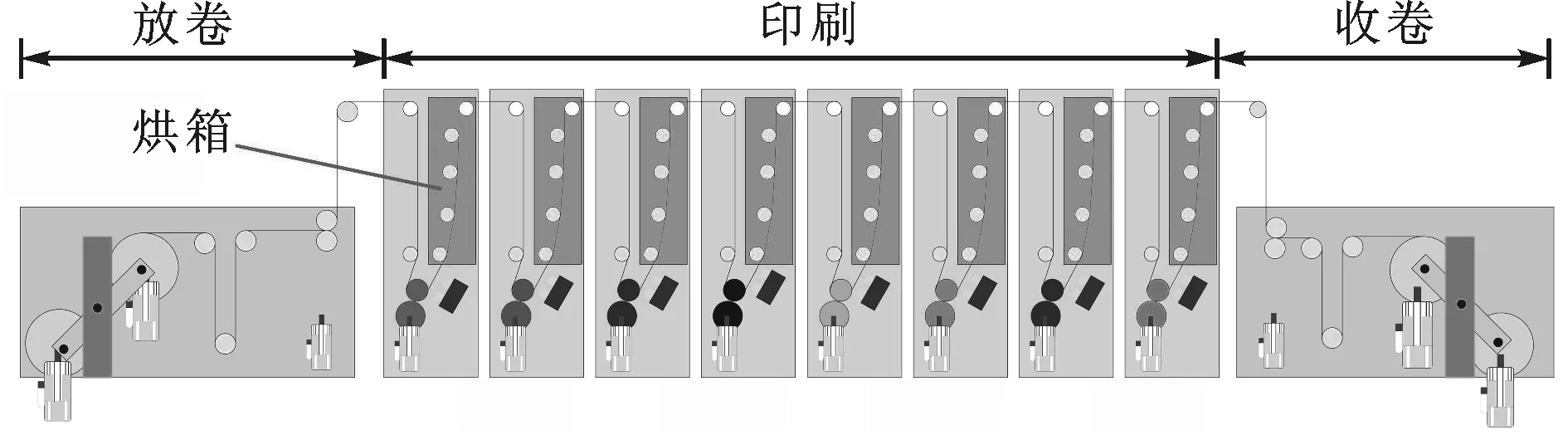
圖1 電子軸傳動(dòng)凹版印刷機(jī)系統(tǒng)組成
在印刷部分,每個(gè)印刷單元都由獨(dú)立的伺服電機(jī)驅(qū)動(dòng),即所謂的電子軸傳動(dòng)或無軸傳動(dòng),取代傳統(tǒng)的機(jī)械長軸結(jié)構(gòu)。該變化使得機(jī)械結(jié)構(gòu)復(fù)雜程度降低,但對控制系統(tǒng)提出了較高的要求。
圖2所示為兩色印刷子系統(tǒng)及料帶溫度分布示意圖,該子系統(tǒng)由兩個(gè)印刷單元、料帶以及烘箱組成,是多色印刷系統(tǒng)的基本張力單元。在該料帶張力子系統(tǒng)中,Ti-1、vi-1和vi分別為輸入量,Ti為輸出量,其他參數(shù)可看作是系統(tǒng)結(jié)構(gòu)參數(shù),故該系統(tǒng)是一個(gè)典型的多輸入-單輸出系統(tǒng)。
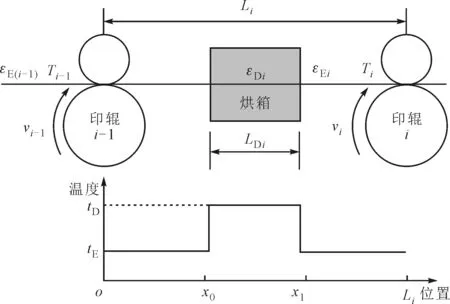
Ti-1為前一區(qū)間的料帶張力;Ti為當(dāng)前區(qū)間的料帶張力;vi-1和vi分別為兩個(gè)印刷版輥的線速度;Li為當(dāng)前區(qū)間內(nèi)的料帶長度;LDi為當(dāng)前區(qū)間烘箱內(nèi)的料帶長度;εE(i-1)為前一區(qū)間烘箱外部的料帶應(yīng)變;εEi為當(dāng)前區(qū)間烘箱外部的料帶應(yīng)變;εDi為當(dāng)前區(qū)間烘箱內(nèi)部料帶的料帶應(yīng)變
由于烘箱的存在,區(qū)間內(nèi)料帶所處的環(huán)境溫度將呈不均勻分布狀態(tài)。由于料帶非常薄,一般為20~100 μm,傳熱過程非常短暫,時(shí)間近乎于0。因此,可以認(rèn)為烘箱內(nèi)部料帶溫度等于烘箱的烘干溫度,烘箱外部的料帶溫度等于車間環(huán)境溫度。故料帶的溫度分布可近似為如圖2所示的狀態(tài)。
在當(dāng)前區(qū)間,單位時(shí)間內(nèi)料帶質(zhì)量的變化量等于進(jìn)入該區(qū)間的料帶質(zhì)量與流出該區(qū)間的料帶質(zhì)量之差,即質(zhì)量守恒,用公式表示為
Δmi=mi,in-mi,out
(1)
將質(zhì)量、密度和體積的關(guān)系表達(dá)式m=ρV代入式(1),得到詳細(xì)的質(zhì)量守恒公式
ρi-1(Li-1,t)Ai-1(Li-1,t)vi-1(t)-
ρi(Li,t)Ai(Li,t)vi(t)
(2)
式中:ρ為料帶密度;A為料帶橫截面積;x為沿料帶運(yùn)動(dòng)方向區(qū)間內(nèi)的位置。
假設(shè)料帶材料是純彈性體,則料帶微單元的質(zhì)量不隨拉伸狀態(tài)改變,即
ρAdx=ρuAudxu
(3)
式中:下標(biāo)u表示料帶的未拉伸狀態(tài)。根據(jù)應(yīng)變定義,式(3)可以寫成
(4)
式中:ε是料帶在運(yùn)動(dòng)方向的應(yīng)變。結(jié)合式(2)和式(4),可以得到
(5)
處于未拉伸狀態(tài)的料帶不隨位置和時(shí)間而變化,故
ρui(x,t)Aui(x,t)=
ρu(i-1)(Li-1,t)Au(i-1)(Li-1,t)=
ρui(Li,t)Aui(Li,t)
(6)
根據(jù)式(6),式(5)可以寫成
(7)
料帶溫度在區(qū)間內(nèi)為不均勻分布狀態(tài),結(jié)合圖2的料帶溫度分布狀態(tài),對積分部分進(jìn)行計(jì)算
(8)
在烘箱內(nèi)部的料帶應(yīng)變處處相同,即εi(x,t)=εDi(t)。同理,烘箱外部的料帶應(yīng)變?chǔ)舏(x,t)=εEi(t),計(jì)算式(8)得到
(9)
式中:εi-1(Li-1,t)和εi(Li,t)均為輥?zhàn)游恢玫牧蠋?yīng)變,處于烘箱外部,所以
εi-1(Li-1,t)=εE(i-1)(t)
(10)
εi(Li,t)=εEi(t)
(11)
結(jié)合式(9)~式(11),式(7)可化簡為
(12)
由于應(yīng)變?chǔ)欧浅P?故
(13)
將式(13)代入式(12),得到
LDi(t)[1-εDi(t)]}=[1-εE(i-1)(t)]vi-1(t)-
[1-εEi(t)]vi(t)
(14)
機(jī)械結(jié)構(gòu)和料帶的路徑是固定不變的,故可忽略料帶長度Li和LDi的變化,則式(14)可以寫成
[1-εE(i-1)(t)]vi-1(t)-[1-εEi(t)]vi(t)
(15)
溫度從兩個(gè)方面對料帶材料產(chǎn)生影響:材料的彈性模量和熱膨脹系數(shù)。料帶在區(qū)間內(nèi)移動(dòng)時(shí)存在膨脹和收縮現(xiàn)象,但對于整個(gè)料帶區(qū)間來說,溫度分布狀態(tài)是固定的,由此引起的熱應(yīng)變也是個(gè)常數(shù)。熱應(yīng)變可以看作是一個(gè)結(jié)構(gòu)參數(shù),在系統(tǒng)初始化的時(shí)候可進(jìn)行補(bǔ)償,由溫度引起的熱應(yīng)變不會(huì)對料帶張力產(chǎn)生影響,因此可以認(rèn)為料帶張力只與料帶的彈性應(yīng)變有關(guān)。根據(jù)胡克定律T=AEε,可以得到
(16)
式中:EE是車間環(huán)境溫度下的楊氏彈性模量;ED是烘干溫度下的楊氏彈性模量。由于車間環(huán)境溫度處處相等,則EE=EE(i-1)=EEi。假設(shè)所有烘箱的烘干溫度相同,則ED=ED(i-1)=EDi。忽略料帶橫截面積的變化,即A=ADi=AE(i-1)=AEi,則式(16)可以表示為
(17)
進(jìn)而簡化為
[AEE-Ti(t)]vi(t)-[AEE-Ti-1(t)]vi-1(t)
(18)
式(18)即為電子軸傳動(dòng)凹印機(jī)印刷張力系統(tǒng)的數(shù)學(xué)模型,其中包含了干燥系統(tǒng)的影響。從數(shù)學(xué)模型可以看出,干燥系統(tǒng)主要通過兩個(gè)方面對料帶張力產(chǎn)生影響,即烘干溫度下的楊氏彈性模量ED和烘箱內(nèi)的料帶長度LDi。烘箱內(nèi)的料帶長度LDi屬于結(jié)構(gòu)參數(shù),在系統(tǒng)運(yùn)行中是常數(shù),因此本文不做深入研究。烘干溫度對料帶張力特性的影響是本文的研究重點(diǎn)。
2 烘干溫度對張力的影響
為了進(jìn)一步分析電子軸凹版印刷系統(tǒng)中烘干溫度對印刷段張力的影響,利用MATLAB/Simulink對數(shù)學(xué)模型進(jìn)行數(shù)值仿真分析,并在電子軸凹版印刷實(shí)驗(yàn)裝置上進(jìn)行實(shí)驗(yàn)驗(yàn)證。
圖3所示為電子軸凹版印刷實(shí)驗(yàn)裝置,包括放卷、印刷和收卷3個(gè)部分。印刷部分的每個(gè)色組都由獨(dú)立伺服電機(jī)YASKAWA SGMGH-44驅(qū)動(dòng),通過伺服電機(jī)上的編碼器信息獲得印輥速度,通過張力傳感器MITSUBISHI LX-030TD獲取料帶張力信號(hào),并進(jìn)一步由張力放大器MITSUBISHI LM-10TA進(jìn)行放大處理。控制系統(tǒng)采用的多軸運(yùn)動(dòng)控制器GOOGOLTECH T8VME(固高科技(深圳)有限公司)。料帶材料為BOPP。為了驗(yàn)證模型,實(shí)驗(yàn)裝置采用開環(huán)控制系統(tǒng),對區(qū)間的料帶張力不進(jìn)行控制。

圖3 電子軸凹版印刷實(shí)驗(yàn)裝置
在圖2中,令i=2,則印刷張力系統(tǒng)的數(shù)學(xué)模型可以寫成
[AEE-T2(t)]v2(t)-[AEE-T1(t)]v1(t)
(19)
仿真所用的設(shè)備機(jī)械參數(shù)與實(shí)際電子軸凹版印刷機(jī)相同,如表1所示。

表1 電子軸凹版印刷機(jī)械參數(shù)

2.1 輸入為T1(t)時(shí)的張力階躍響應(yīng)
前一區(qū)間的料帶張力T1(t)產(chǎn)生一個(gè)幅值為10 N的階躍信號(hào),當(dāng)前區(qū)間的料帶張力T2(t)在不同烘干溫度條件下的階躍響應(yīng)仿真和實(shí)驗(yàn)結(jié)果如圖4所示。其中,tD=20 ℃表示烘干溫度與室溫相同,即無干燥系統(tǒng)時(shí)的響應(yīng)。tD=60 ℃和tD=80 ℃表示兩個(gè)不同的烘干溫度時(shí)系統(tǒng)的階躍響應(yīng)。從圖4可以看出:在輸入為T1(t)時(shí),不同烘干溫度下T2(t)的階躍響應(yīng)都表現(xiàn)為正向階躍輸出;干燥系統(tǒng)的存在對系統(tǒng)特性有顯著的影響;烘干溫度只影響瞬態(tài)響應(yīng)部分,不影響穩(wěn)態(tài)響應(yīng)。
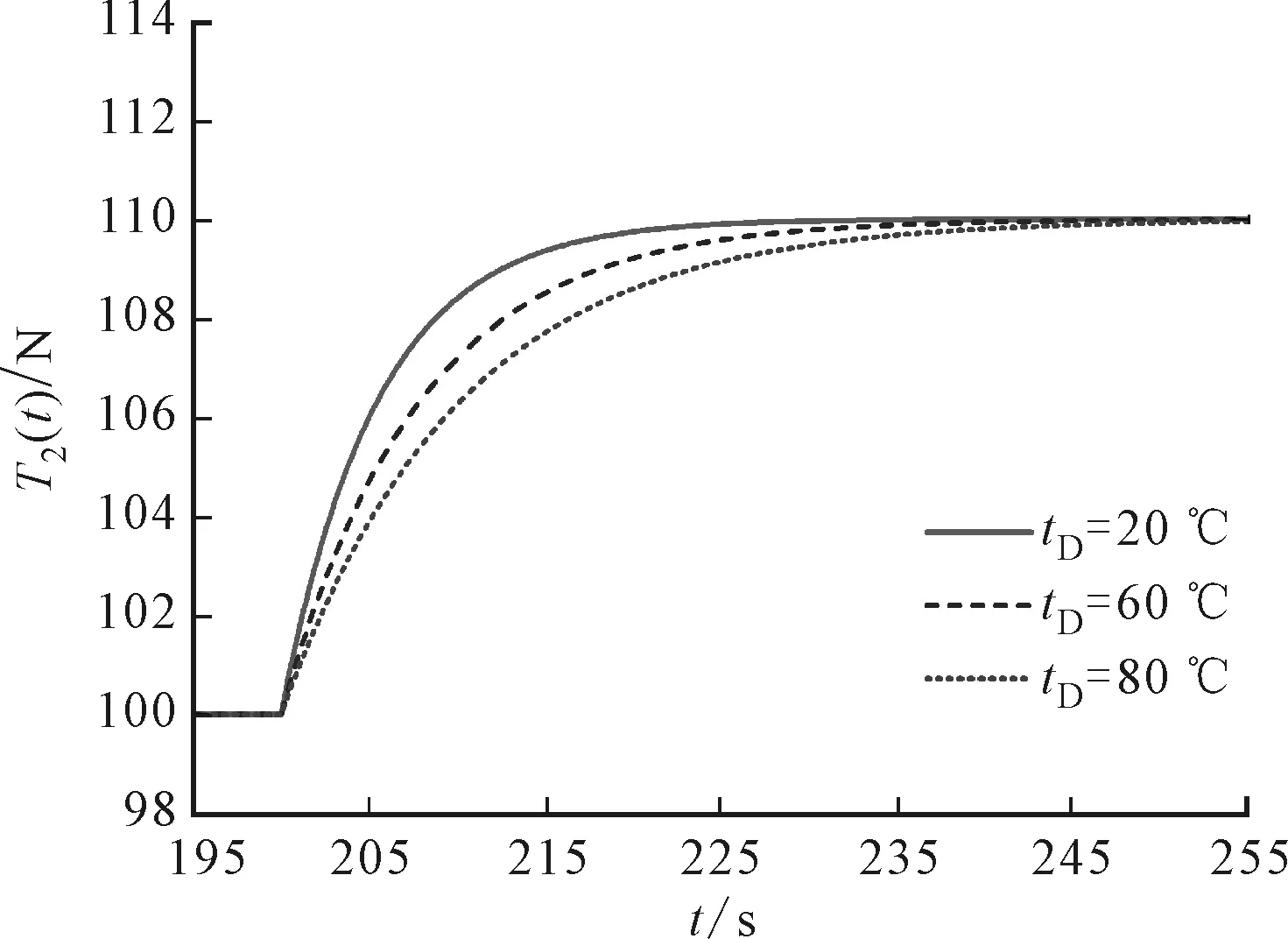
(a)仿真結(jié)果
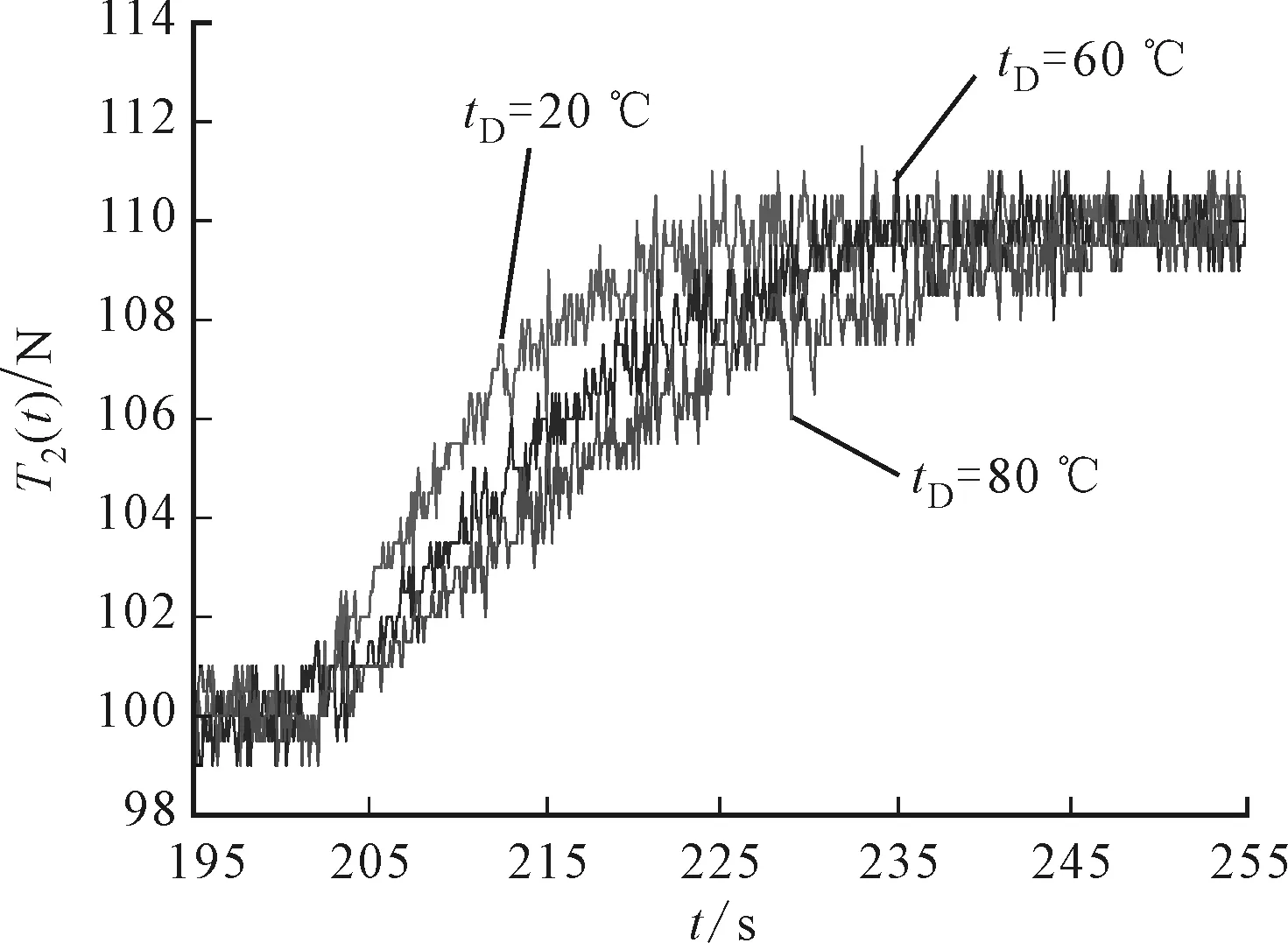
(b)實(shí)驗(yàn)結(jié)果
在圖4a中,對于穩(wěn)態(tài)響應(yīng)部分,無論烘干溫度為多少,穩(wěn)態(tài)值都增大了10 N,與輸入量T1(t)的增量相等,即烘干溫度不影響由T1(t)引起的穩(wěn)態(tài)響應(yīng)。對于瞬態(tài)響應(yīng)部分,在20、60和80 ℃情況下的過渡過程時(shí)間分別為22、31和40 s。相對于沒有干燥系統(tǒng)情況下,烘干溫度分別為60 ℃和80 ℃時(shí),過渡過程時(shí)間分別增大了41%和82%。可以看出,烘干溫度越高,瞬態(tài)響應(yīng)的過渡過程時(shí)間越長。干燥系統(tǒng)對瞬態(tài)響應(yīng)的影響較大,因此實(shí)際應(yīng)用中不能忽略烘干溫度對張力特性的影響。
圖4b所示為實(shí)驗(yàn)結(jié)果,采樣周期為100 ms。實(shí)驗(yàn)曲線的過渡時(shí)間長度較仿真曲線長,其原因在于實(shí)驗(yàn)中輸入的料帶張力T1(t)不是直接獲得,而是通過調(diào)整前級(jí)輥?zhàn)愚D(zhuǎn)速獲得的。此外,整個(gè)實(shí)驗(yàn)過程(階躍響應(yīng)前后)都有一定的張力波動(dòng),這與機(jī)械系統(tǒng)的振動(dòng)和采集系統(tǒng)的噪聲有關(guān),屬于正常的系統(tǒng)干擾。實(shí)驗(yàn)結(jié)果的整體趨勢與仿真結(jié)果吻合,說明所建模型的正確性。
2.2 輸入為v1(t)時(shí)的張力階躍響應(yīng)
當(dāng)前區(qū)間版輥的線速度v1(t)產(chǎn)生一個(gè)幅值為0.02 m/min的階躍信號(hào),當(dāng)前區(qū)間的料帶張力T2(t)在不同烘干溫度條件下的階躍響應(yīng)仿真和實(shí)驗(yàn)結(jié)果如圖5所示。可以看出,在輸入為v1(t)時(shí),不同烘干溫度下T2(t)的階躍響應(yīng)都表現(xiàn)為負(fù)向階躍輸出;干燥系統(tǒng)對系統(tǒng)特性有顯著的影響;烘干溫度只影響瞬態(tài)響應(yīng)部分,不影響穩(wěn)態(tài)響應(yīng)。
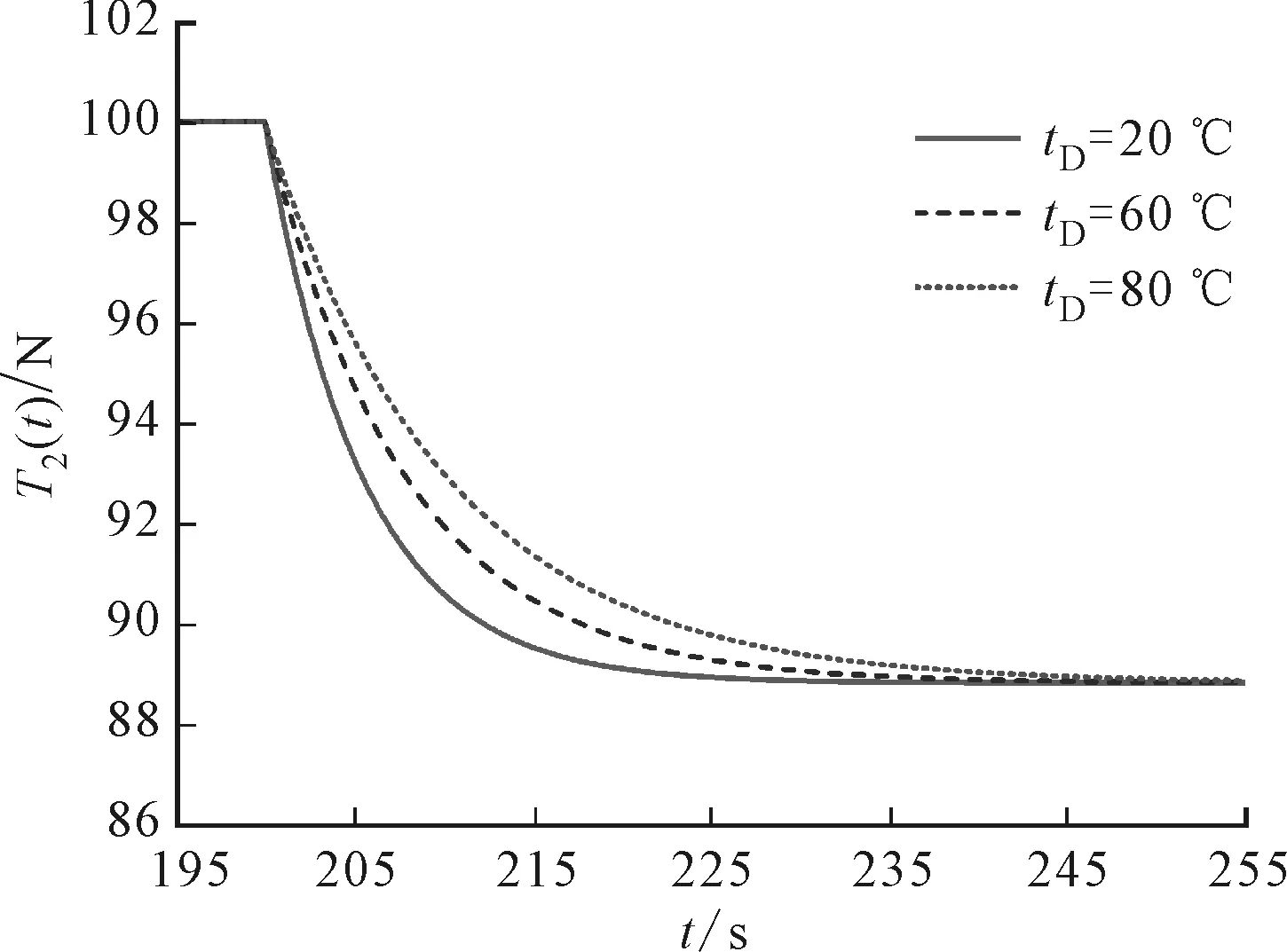
(a)仿真結(jié)果

(b)實(shí)驗(yàn)結(jié)果
在圖5a中,對于穩(wěn)態(tài)響應(yīng)部分,無論烘干溫度為多少,穩(wěn)態(tài)值都減小了11.2 N,即烘干溫度不影響由v1(t)引起的穩(wěn)態(tài)響應(yīng)。對于瞬態(tài)響應(yīng)部分,在20、60和80 ℃情況下的過渡過程時(shí)間分別為22、31和40 s,與輸入為T1(t)時(shí)的結(jié)果相同。與2.1節(jié)類似,烘干溫度越高,瞬態(tài)響應(yīng)的過渡過程時(shí)間越長,干燥系統(tǒng)對瞬態(tài)響應(yīng)的影響顯著。圖5b的實(shí)驗(yàn)結(jié)果整體趨勢與仿真結(jié)果吻合。
2.3 輸入為v2(t)時(shí)的張力階躍響應(yīng)
當(dāng)前區(qū)間版輥的線速度v2(t)產(chǎn)生一個(gè)幅值為0.02 m/min的階躍信號(hào),當(dāng)前區(qū)間的料帶張力T2(t)在不同烘干溫度條件下的階躍響應(yīng)仿真和實(shí)驗(yàn)結(jié)果如圖6所示。從中可以看出:在輸入為v2(t)時(shí),不同烘干溫度下T2(t)的階躍響應(yīng)都表現(xiàn)為正向階躍輸出;干燥系統(tǒng)對系統(tǒng)特性有顯著的影響;烘干溫度只影響瞬態(tài)響應(yīng)部分,不影響穩(wěn)態(tài)響應(yīng)。
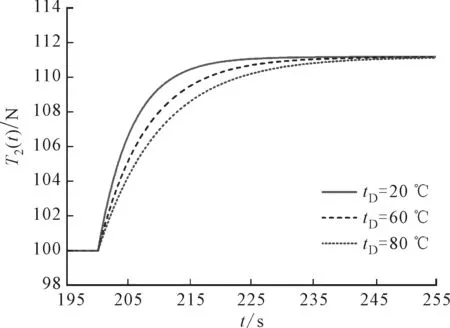
(a)仿真結(jié)果
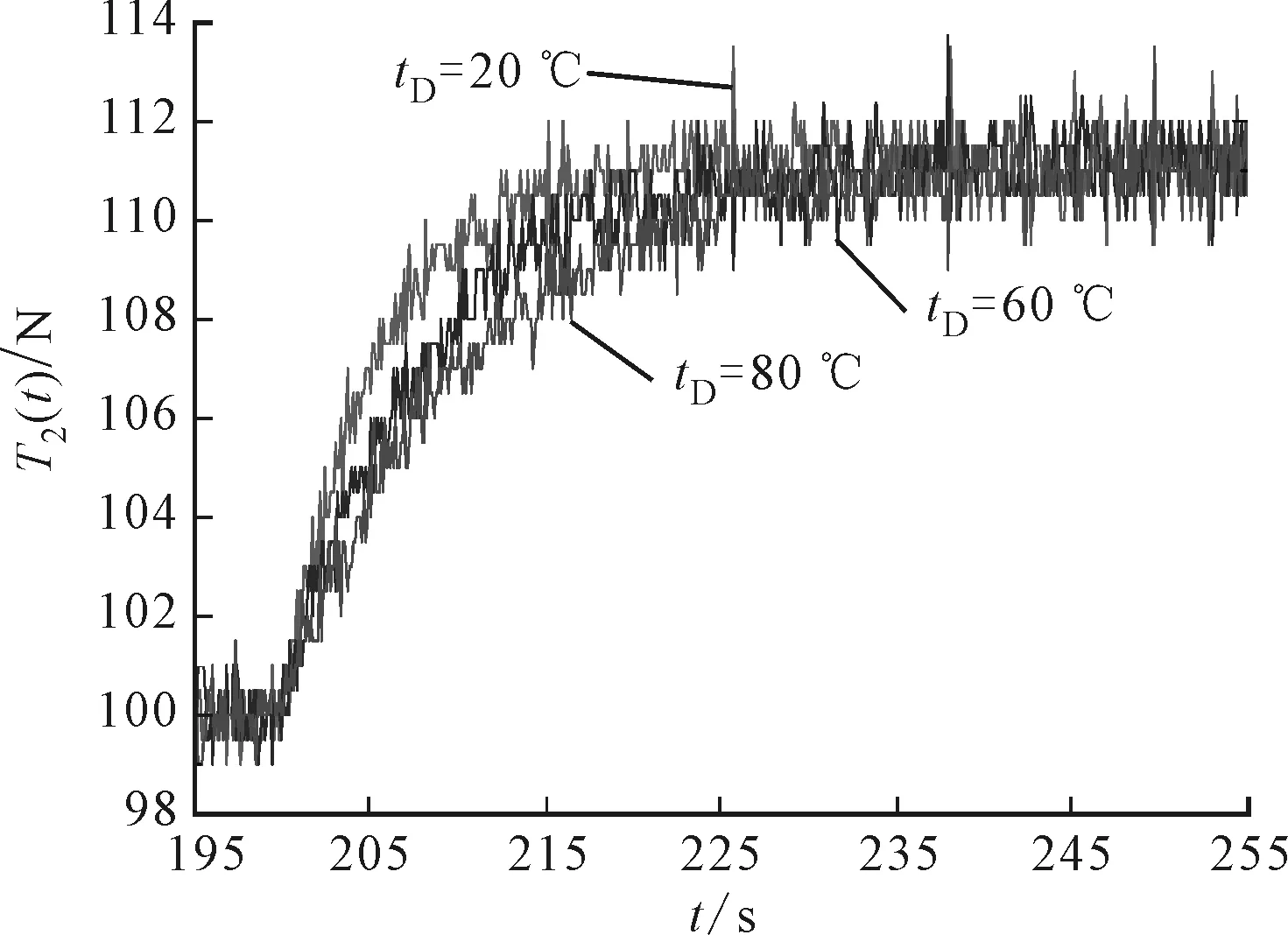
(b)實(shí)驗(yàn)結(jié)果
圖6a中對于穩(wěn)態(tài)響應(yīng)部分,穩(wěn)態(tài)值在不同烘干溫度下均增大了11.2 N,即烘干溫度不影響由v2(t)引起的穩(wěn)態(tài)響應(yīng)。對于瞬態(tài)響應(yīng)部分,在20、60和80 ℃情況下的過渡過程時(shí)間分別為22、31和40 s,與輸入為T1(t)和v1(t)時(shí)的數(shù)值相同。與2.1節(jié)和2.2節(jié)類似,烘干溫度越高,瞬態(tài)響應(yīng)的過渡過程時(shí)間越長,干燥系統(tǒng)對瞬態(tài)響應(yīng)的影響顯著。圖6b的實(shí)驗(yàn)結(jié)果整體趨勢與仿真結(jié)果吻合。
3 結(jié) 論
為了提高電子軸凹版印刷精度,需要對包含干燥系統(tǒng)的印刷部分的張力模型進(jìn)行深入研究。本文首先根據(jù)質(zhì)量守恒規(guī)律建立了包含溫度因素的印刷部分張力模型,該數(shù)學(xué)模型顯示干燥系統(tǒng)可以通過料帶的楊氏彈性模量對張力系統(tǒng)產(chǎn)生影響。通過系統(tǒng)的階躍響應(yīng)數(shù)值仿真和實(shí)驗(yàn)研究發(fā)現(xiàn),烘干溫度對系統(tǒng)穩(wěn)態(tài)響應(yīng)沒有影響,而對系統(tǒng)瞬態(tài)響應(yīng)影響較大。瞬態(tài)響應(yīng)的過渡過程時(shí)間隨著烘干溫度的增高而增長,在本文給定條件下,烘干溫度為60~80 ℃時(shí),過渡過程時(shí)間相比于無干燥系統(tǒng)增長了41%~82%。干燥系統(tǒng)對印刷部分的張力系統(tǒng)特性影響顯著,在印刷部分的張力系統(tǒng)和套準(zhǔn)系統(tǒng)研究中成為不可忽略的重要因素。本文研究為電子軸凹版印刷的套準(zhǔn)系統(tǒng)提供理論基礎(chǔ),有利于進(jìn)一步提高電子軸凹版印刷的產(chǎn)品質(zhì)量。

