移動邊緣計算中分布式的設(shè)備發(fā)射功率優(yōu)化算法

周文晨,方維維,李陽陽,薛峰,王子岳

(1.北京交通大學(xué)計算機(jī)與信息技術(shù)學(xué)院,100044,北京;2.中國電子科學(xué)研究院創(chuàng)新中心,100041,北京)

近年來,移動互聯(lián)網(wǎng)快速發(fā)展,移動用戶設(shè)備數(shù)量呈指數(shù)爆炸式增長[1],移動計算需求不斷升級。根據(jù)思科公司最新預(yù)測報告顯示,2021年全球移動數(shù)據(jù)流量將比2016年增長7倍,全球移動設(shè)備數(shù)量將增加到116億[2],但目前以長距離數(shù)據(jù)傳輸和集中式大數(shù)據(jù)處理為特點的移動云計算不僅占用大量網(wǎng)絡(luò)帶寬,而且傳輸時延較大,已無法滿足時延敏感型業(yè)務(wù),例如無人駕駛汽車、醫(yī)療大數(shù)據(jù)和智慧城市等的需求[3]。

歐洲電信標(biāo)準(zhǔn)化研究所(ETSI)在2014年首次提出移動邊緣計算(MEC),移動設(shè)備可將高復(fù)雜度、高能耗計算任務(wù)卸載到MEC系統(tǒng)的接入網(wǎng)邊緣節(jié)點,例如基站、無線接入點等,從而獲得低時延、近距離的本地化云服務(wù)[4]。MEC系統(tǒng)結(jié)合了移動通信[5]和云計算[6]兩種技術(shù),通過協(xié)同優(yōu)化通信和計算資源實現(xiàn)低能耗、低時延的計算卸載服務(wù)。目前,最新的MEC系統(tǒng)研究將關(guān)注點放在單服務(wù)器多用戶條件下的通信、計算資源分配控制,以實現(xiàn)總體能耗最優(yōu)。Mao等基于隨機(jī)優(yōu)化模型的優(yōu)化方法,聯(lián)合本地計算功率、最優(yōu)發(fā)射功率和無線帶寬資源等約束對移動設(shè)備能耗進(jìn)行優(yōu)化,但是卻無法有效約束時延,且計算復(fù)雜度較大,沒有考慮某個區(qū)域內(nèi)MEC系統(tǒng)的整體部署優(yōu)化[7];Liu等通過采用馬爾可夫決策過程理論對任務(wù)隊列的排隊屬性進(jìn)行分析,提出了發(fā)射功率約束條件下的最小化處理時延的問題,但忽略了設(shè)備的能耗[8];You等針對TDMA、OFDMA兩種網(wǎng)絡(luò)工作模式,通過確定卸載量和時間槽,解決卸載通信和本地計算總體能耗最小化的凸優(yōu)化問題,但是所提算法需要依賴于本機(jī)計算能量和信道增益的先驗知識做出資源分配策略,降低了實際場景的可用性[9]。

綜上所述,本文以MEC系統(tǒng)的多服務(wù)器、多用戶的大規(guī)模場景下的計算卸載的時延和能耗的平衡為研究目標(biāo),基于邊緣計算的通信和計算資源的耦合約束,設(shè)計一種基于馬爾可夫近似的分布式發(fā)射功率優(yōu)化算法(TPO)。該算法基于馬爾可夫狀態(tài)概率跳轉(zhuǎn)規(guī)則設(shè)計,移動用戶設(shè)備自主決策計算卸載的服務(wù)器對象,從而有效降低系統(tǒng)級用戶功耗。理論證明,分布式TPO算法具有穩(wěn)態(tài)概率分布的馬爾可夫鏈,所設(shè)計的轉(zhuǎn)移速率滿足馬爾可夫鏈的狀態(tài)相互轉(zhuǎn)換條件;實驗仿真結(jié)果表明,所提算法顯著優(yōu)于基準(zhǔn)算法,并在有效時間內(nèi)逼近最優(yōu)解決方案。

1 MEC系統(tǒng)建模

本文研究的MEC系統(tǒng)場景示例如圖1所示。根據(jù)已有的相關(guān)研究,本文基于以下5種假設(shè):①每個邊緣服務(wù)器時間和頻率完全同步;②每個邊緣服務(wù)器上的每個載波的信道增益在特定時間內(nèi)保持恒定;③由于每個邊緣服務(wù)器的載波頻率不同,假設(shè)MEC系統(tǒng)中邊緣服務(wù)器間不存在信號干擾;④設(shè)備同一時刻只能與一個邊緣服務(wù)器進(jìn)行連通;⑤卸載所需要執(zhí)行的指令都可以利用邊緣服務(wù)器進(jìn)行處理[10-13]。

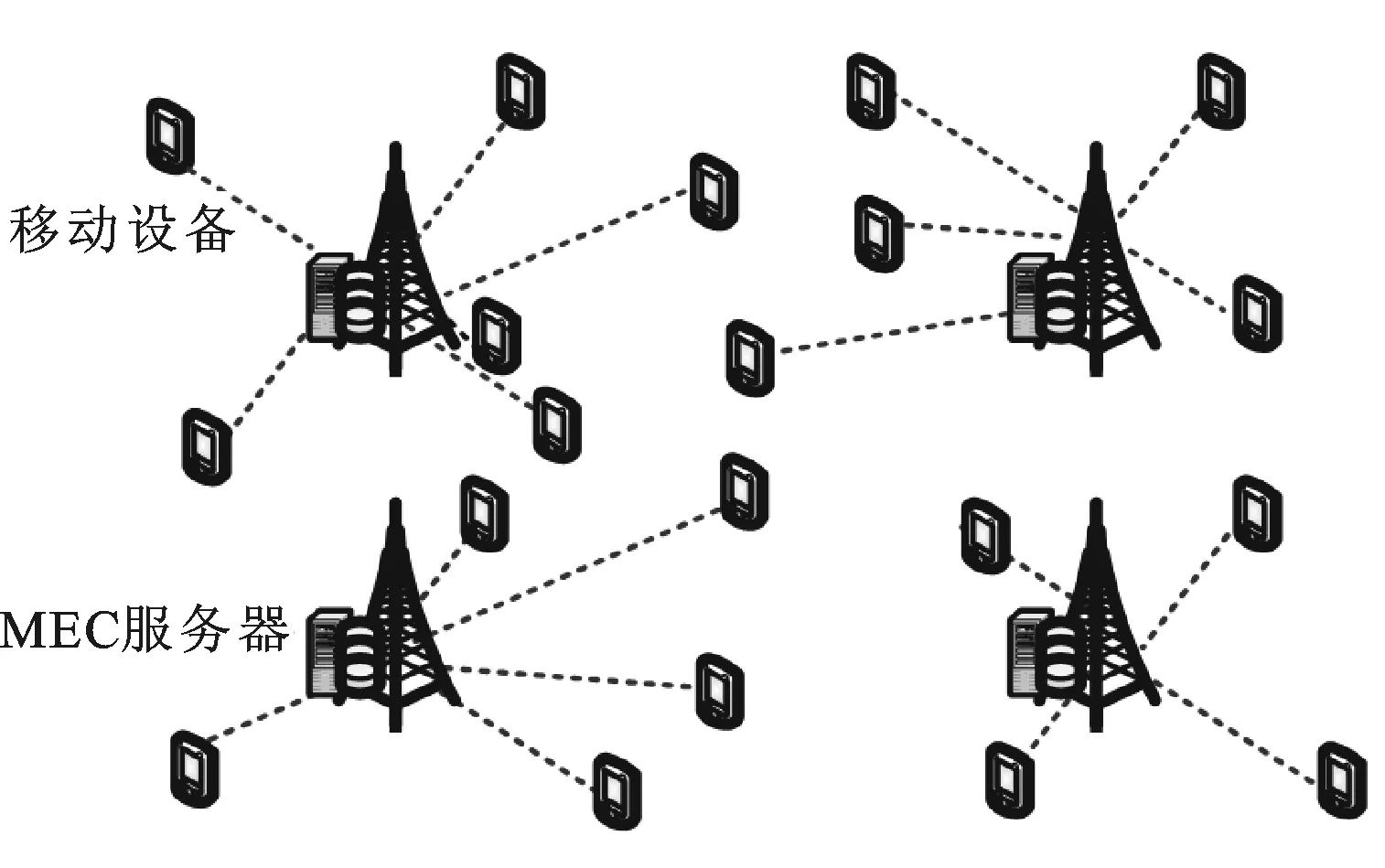
圖1 多MEC服務(wù)器多用戶設(shè)備場景示例

假設(shè)當(dāng)前區(qū)域內(nèi)有M個邊緣服務(wù)器X={1,2,…,M}和N個移動用戶設(shè)備Y={1,2,…,N}。每個移動用戶設(shè)備n的計算任務(wù)卸載到邊緣服務(wù)器m,設(shè)備n必須傳送所有信息到服務(wù)器m。設(shè)定執(zhí)行程序的參數(shù):①每秒輸入比特數(shù);②需要被MEC服務(wù)器執(zhí)行計算的指令集;③每秒輸出比特數(shù)。對于移動用戶設(shè)備n所需要卸載到服務(wù)器m的計算任務(wù)的輸入數(shù)據(jù)大小為Cmn,執(zhí)行的指令數(shù)為Dmn=Dmn(Cmn)。設(shè)備n是否卸載計算任務(wù)到服務(wù)器m主要取決于如下因素:需要被處理的指令數(shù)、設(shè)備n與對應(yīng)服務(wù)器m之間的無線信道狀況和服務(wù)器m的并行多個進(jìn)程的能力大小,同時每個進(jìn)程為了用戶的滿意體驗都規(guī)定了不應(yīng)超過的最大時延[14],因此移動用戶設(shè)備n決定卸載計算任務(wù)到服務(wù)器m之前必須考慮時延約束。在沒有解碼錯誤的前提下,用戶設(shè)備n的時延應(yīng)該包含將輸入信息傳輸?shù)綄?yīng)服務(wù)器m的時間、服務(wù)器m執(zhí)行指令所需的時間和將結(jié)果返回給設(shè)備n的時間。

根據(jù)香農(nóng)定理,在加性白高斯噪聲(AWGN)、信道帶寬為B的信道上傳送Cmn數(shù)據(jù)所需的最小時間為

(1)

式中:Pn是設(shè)備n計算任務(wù)卸載的發(fā)射功率;|Hmn|2是信道衰落系數(shù)(歸一化距離);Gmn是信噪比裕度;dmn是設(shè)備n和相連MEC服務(wù)器m的物理距離;γ是路徑損耗指數(shù);N0是噪聲功率。Pn是可調(diào)功率,Pn∈S,S是有限離散集合。

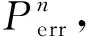
(2)

服務(wù)器m執(zhí)行指令所需的時間與其資源分配方式有直接關(guān)聯(lián)。系統(tǒng)內(nèi)用戶設(shè)備與服務(wù)器的連接方式表示為

(3)

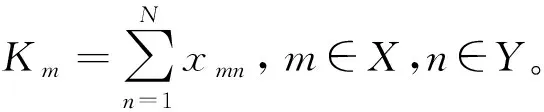
(4)

忽略服務(wù)器m把計算結(jié)果返回給設(shè)備n的極短時間[11],則設(shè)備n的平均計算卸載的時延為

(5)

(6)

Pn∈S,n∈Y

xmn∈{0,1},m∈X,n∈Y

基于香農(nóng)定理和鏈路傳輸特性將用戶功率最小化策略建模成問題(6),作為典型的組合網(wǎng)絡(luò)優(yōu)化問題,其求解復(fù)雜度是NP難的,一般只能通過集中式的窮舉搜索獲得最優(yōu)解[15],可行解空間隨著網(wǎng)絡(luò)規(guī)模的增大而呈指數(shù)級增加,而隨機(jī)法又不能獲得穩(wěn)定而較優(yōu)的解,因此有必要尋求一種有效和穩(wěn)定的求解方法。

2 TPO算法設(shè)計

針對問題(6),設(shè)計了一種分布式并發(fā)的優(yōu)化算法,利用Log-Sum-Exp函數(shù)[15]將問題轉(zhuǎn)化為最小權(quán)重配置的近似問題,然后使用馬爾可夫近似[15]求解問題,即通過求解轉(zhuǎn)化后的問題從而趨近問題(6)的最優(yōu)解,并證明算法可進(jìn)行有效求解。

2.1 Log-Sum-Exp原則

設(shè)定配置f={xmn,m∈X,n∈Y},即問題(6)所表示的系統(tǒng)中移動用戶設(shè)備n和邊緣服務(wù)器m相連的可行配置狀態(tài),所有可行的狀態(tài)f組成F,即f∈F,則問題(6)的等效問題模型是

(7)

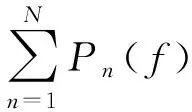
問題(7)是NP難的網(wǎng)絡(luò)組合優(yōu)化問題,對實際系統(tǒng)來說可行集合F非常大,因此通過Log-Sum-Exp函數(shù),將問題(7)近似轉(zhuǎn)化為

(8)

式中β是正的常數(shù)。因為問題(8)的目標(biāo)函數(shù)對于所有的ρf是二次可微、單調(diào)遞增和嚴(yán)格的凹函數(shù),其所有的約束都是線性的,所以Karush-Kuhn-Tucker(KKT)條件對于最優(yōu)解是必要和充分的,故問題(8)的最優(yōu)解是

(9)

與原問題(6)相比,近似問題(8)存在一個額外的熵項,即為優(yōu)化差距,通過對比兩問題的表達(dá)式可知優(yōu)化差距的上限是

(10)

從式(10)可知,優(yōu)化差距上限的大小取決于β,當(dāng)β增加時,優(yōu)化差距上限會減小,這意味著近似求解結(jié)果更加準(zhǔn)確,優(yōu)化差距上限r(nóng)*=lb|F|/β,此時ρf=1/|F|,f∈F,同時由文獻(xiàn)[16]可知,當(dāng)β增加時,收斂時間將增加。

綜上可知,當(dāng)β增加時,近似求解獲得的系統(tǒng)移動用戶設(shè)備發(fā)射總功率更加準(zhǔn)確,因此選擇相對較大的β來獲得穩(wěn)態(tài)分布。通過馬爾可夫近似獲得的近似系統(tǒng)功率可表示為

(11)

2.2 TPO算法設(shè)計

根據(jù)文獻(xiàn)[15]可知,狀態(tài)轉(zhuǎn)移速率有很多設(shè)計選擇,將其設(shè)計為

(12)

馬爾可夫鏈通常具有分布式的結(jié)構(gòu),因此可以設(shè)計分布式算法以實現(xiàn)符合馬爾可夫鏈的移動用戶設(shè)備的決策算法[17]。算法設(shè)計的關(guān)鍵是建立不同配置f之間的鏈接,實現(xiàn)最小化轉(zhuǎn)換配置的系統(tǒng)級功率,通過每次只執(zhí)行一個用戶設(shè)備切換服務(wù)器的選擇來連接系統(tǒng)兩個配置的鏈接。本文將算法命名為發(fā)射功率優(yōu)化(TPO)算法,TPO算法分為以下4個步驟。

步驟1每個移動用戶設(shè)備隨機(jī)選擇MEC服務(wù)器,初始化計算資源和設(shè)備時延約束等信息。

步驟2當(dāng)前狀態(tài)定義為配置f,每個用戶設(shè)備計算自己的發(fā)射功率并廣播,同時生成均值為ζ的指數(shù)分布隨機(jī)數(shù),根據(jù)隨機(jī)數(shù)進(jìn)行倒計時,最先到期的用戶設(shè)備n將隨機(jī)切換到新MEC服務(wù)器,并通知其他所有用戶設(shè)備終止倒計時。

步驟3進(jìn)入新配置f′,每個用戶設(shè)備重新計算自己的發(fā)射功率并廣播。用戶設(shè)備n根據(jù)配置f和f′的系統(tǒng)移動用戶設(shè)備發(fā)射總功率的改變做出決策,以概率ρf,f′停留在新的MEC服務(wù)器或者以概率(1-ρf,f′)切換到原先的MEC服務(wù)器,其中

(13)

步驟4重復(fù)步驟2～步驟4,直至收斂。

2.3 TPO算法可行性證明

定理1TPO算法實現(xiàn)了一個時間可逆的馬爾可夫鏈,其穩(wěn)態(tài)分布如式(9)所示。

證明通過算法步驟2的移動用戶設(shè)備的轉(zhuǎn)換條件可知,所有配置可以在有限轉(zhuǎn)換次數(shù)內(nèi)相互可達(dá),因此構(gòu)造的馬爾可夫鏈?zhǔn)遣豢杉s的。此外,它是具有唯一穩(wěn)態(tài)分布的有限狀態(tài)遍歷馬爾可夫鏈。現(xiàn)在證明穩(wěn)態(tài)分布表達(dá)式是式(9)。

基于式(12)設(shè)定的系統(tǒng)狀態(tài)轉(zhuǎn)移速率可得

(14)

它滿足細(xì)致平衡等式,證畢。

定理2通過上述完備的馬爾可夫鏈設(shè)計,對于任意兩個滿足相互轉(zhuǎn)換條件的配置f,f′∈F,轉(zhuǎn)移速率是式(12)。

證明從系統(tǒng)的角度來看,狀態(tài)f轉(zhuǎn)移到狀態(tài)f′是由于配置f下的設(shè)備n切換服務(wù)器所致,設(shè)備n從已連接的MEC服務(wù)器斷開,隨機(jī)切換到新的服務(wù)器,可切換的服務(wù)器有M-1個。故對于設(shè)備n離開狀態(tài)f轉(zhuǎn)移概率為

其中配置f∈F是馬爾可夫鏈的狀態(tài)之一,因為設(shè)備根據(jù)均值為ζ的指數(shù)分布隨機(jī)數(shù)進(jìn)行倒計時,倒計時結(jié)束后進(jìn)行服務(wù)器切換,因此狀態(tài)f轉(zhuǎn)移到狀態(tài)f′的轉(zhuǎn)移速率為

因此,轉(zhuǎn)移速率與式(12)相等,證畢。

本文算法滿足近似最優(yōu)解,是可行設(shè)計。

3 仿真與結(jié)果分析

3.1 實驗設(shè)置

為了驗證TPO算法的有效性和穩(wěn)定性,采用C++編程進(jìn)行仿真實驗,與隨機(jī)法和窮舉法的實驗結(jié)果進(jìn)行對比,得到關(guān)鍵參數(shù)對系統(tǒng)的影響。參數(shù)設(shè)置見表1[11,18]。移動用戶設(shè)備n的輸入數(shù)據(jù)大小Cmn設(shè)定為(0.2+0.02n)MB,為簡化起見,設(shè)定MEC服務(wù)器執(zhí)行的指令數(shù)Dmn與輸入數(shù)據(jù)大小Cmn成線性相關(guān),即Dmn=σCmn。集合S={0w,10-2w,2×10-2w,…,10w}。

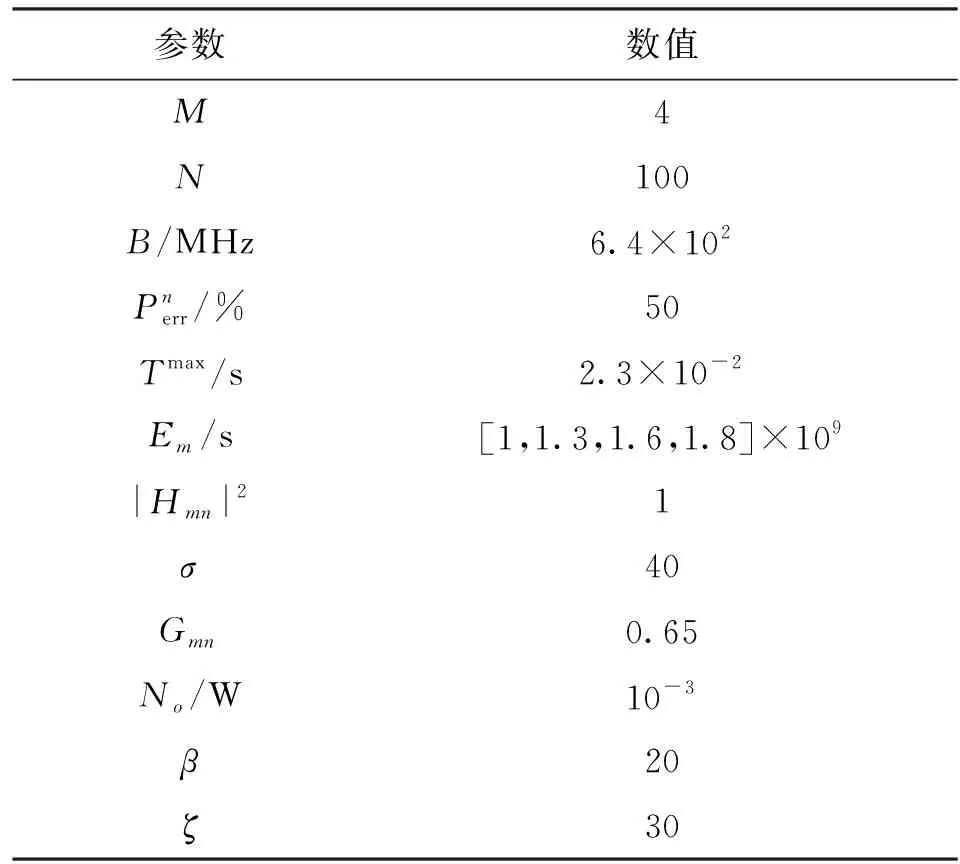
表1 TPO算法仿真參數(shù)

3.2 實驗結(jié)果分析

因采用窮舉搜索獲得系統(tǒng)N個移動用戶設(shè)備與M個MEC服務(wù)器的連接方式的最優(yōu)解共需計算MN次,復(fù)雜度過高,因此我們將TPO算法與隨機(jī)法實驗結(jié)果進(jìn)行對比。圖2分別給出了TPO算法與隨機(jī)法得到的系統(tǒng)用戶設(shè)備發(fā)射總功率。從圖2可知,雖然TPO算法實現(xiàn)的系統(tǒng)用戶設(shè)備發(fā)射總功率平均值在算法執(zhí)行初期比隨機(jī)法平均值大,但是在50次迭代后小于隨機(jī)法平均值。TPO算法實現(xiàn)的總功率均值隨著算法迭代次數(shù)逐步下降,可收斂至4.6 W,而多次隨機(jī)法的均值為21.4 W,由此可推算出TPO算法性能比隨機(jī)法的效果提升了78.5%,因此TPO算法不僅可行,并且得到的收斂解比隨機(jī)法結(jié)果更趨近最優(yōu)解,更加有效。

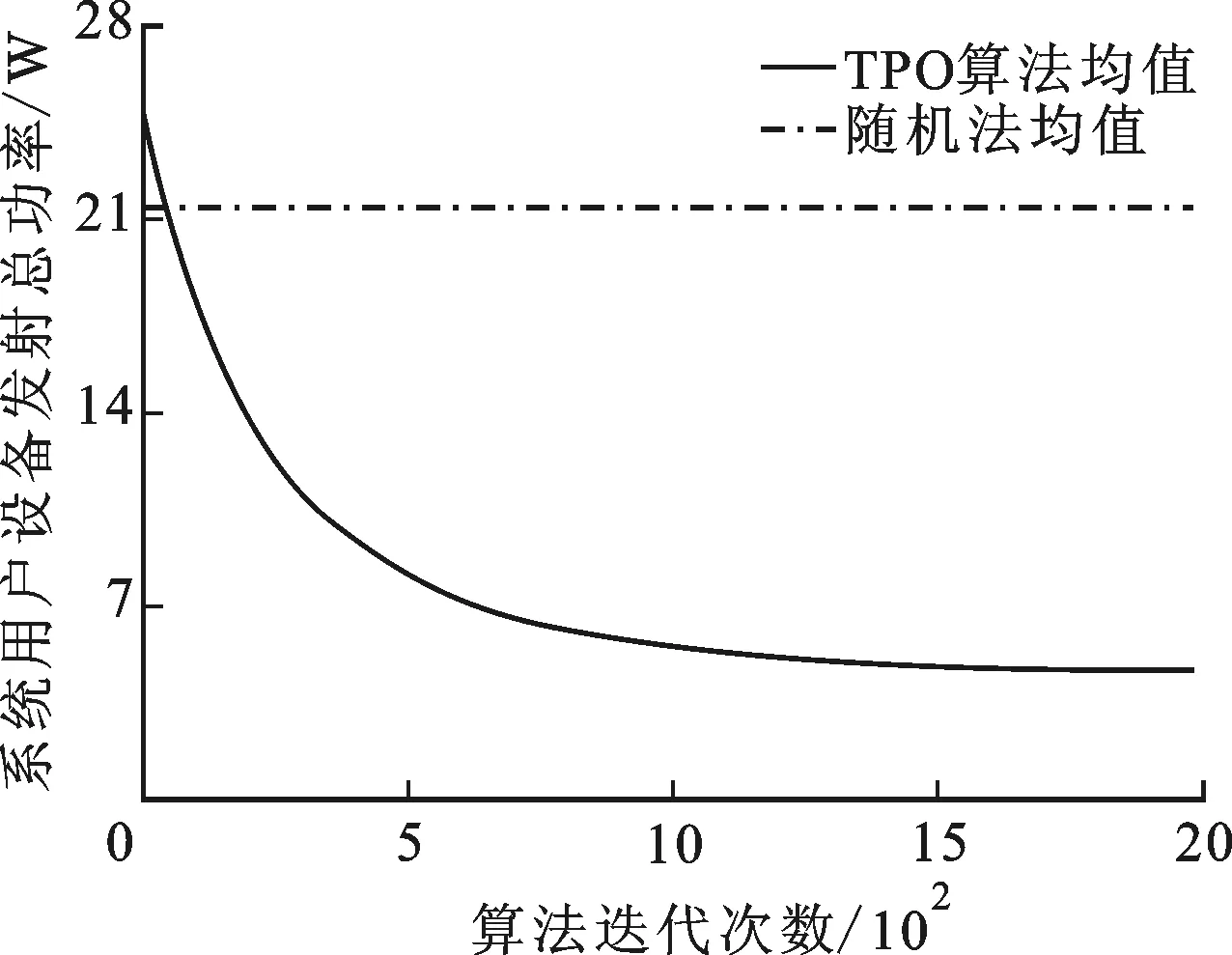
圖2 TPO算法與隨機(jī)法對比

為了進(jìn)一步驗證TPO算法的準(zhǔn)確性,建立4個MEC服務(wù)器服務(wù)10個用戶設(shè)備的小型MEC系統(tǒng)場景,在此場景下對比分析TPO算法多次實驗平均值和窮舉搜索最優(yōu)結(jié)果。圖3給出了TPO算法與窮舉搜索實現(xiàn)的系統(tǒng)用戶設(shè)備發(fā)射總功率。實驗數(shù)據(jù)顯示,TPO算法實現(xiàn)的系統(tǒng)用戶設(shè)備發(fā)射總功率均值僅在第130次迭代后逼近最優(yōu)解,遠(yuǎn)小于理論優(yōu)化差距,與窮舉法的410計算次數(shù)相比,TPO算法復(fù)雜度大大降低,更具有實際應(yīng)用價值。

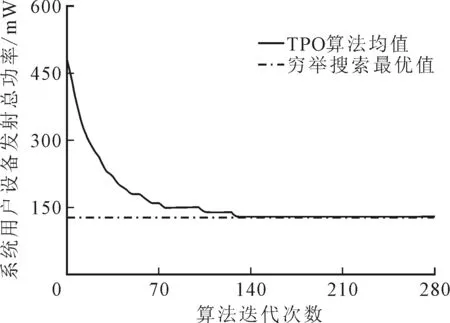
圖3 TPO算法與窮舉搜索結(jié)果對比

以上實驗結(jié)果驗證了TPO算法的有效性和實用性,下面將分析系統(tǒng)關(guān)鍵參數(shù)對TPO算法結(jié)果的影響。圖4顯示了TPO算法的參數(shù)β對算法收斂時間和系統(tǒng)用戶設(shè)備發(fā)射總功率的影響。從圖4中可知,當(dāng)β=20時,系統(tǒng)總功率接近最優(yōu)解,收斂時間較長;當(dāng)β=5時,系統(tǒng)總功率遠(yuǎn)離最優(yōu)解,收斂時間較短。因此伴隨β的增加,TPO算法獲得的近似系統(tǒng)總功率越接近最優(yōu)值,同時收斂時間增加,符合式(10)理論結(jié)果。

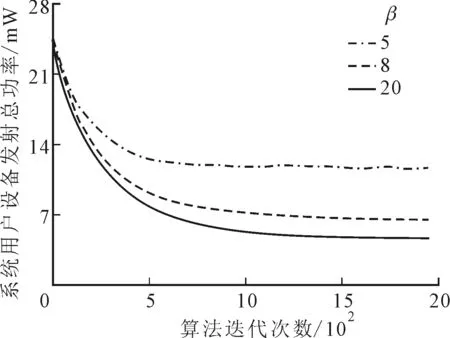
圖4 系統(tǒng)用戶設(shè)備發(fā)射總功率與β的關(guān)系

圖5是將所有移動用戶設(shè)備的輸入數(shù)據(jù)大小Cmn設(shè)定為相同值并統(tǒng)一調(diào)整,觀察系統(tǒng)用戶設(shè)備總功率與設(shè)備所需計算卸載的輸入數(shù)據(jù)量大小Cmn的關(guān)系。從圖5可以看出,當(dāng)Cmn越大,TPO算法實現(xiàn)的系統(tǒng)用戶設(shè)備的總發(fā)射功率會增大,這是因為設(shè)備需要更多的能耗傳輸更多的數(shù)據(jù),但是總發(fā)射功率的收斂時間并沒有伴隨Cmn增加發(fā)生顯著變化,說明當(dāng)設(shè)備的輸入比特量增加時,TPO算法的收斂速度會更快,這對實際系統(tǒng)中用戶設(shè)備計算卸載高峰期的處理具有很大的優(yōu)勢。

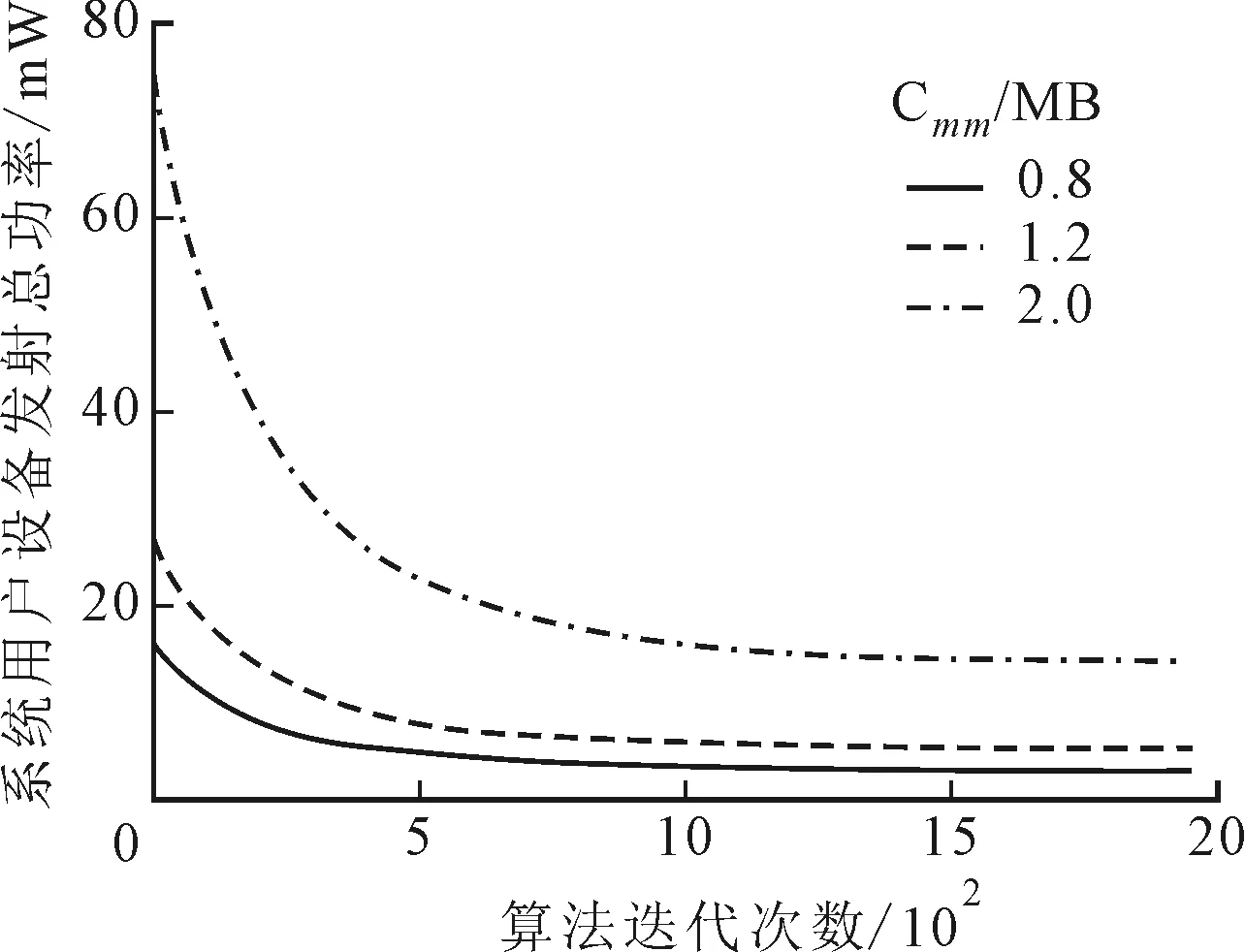
圖5 系統(tǒng)用戶設(shè)備發(fā)射總功率與Cmn的關(guān)系

為了顯示TPO算法對用戶設(shè)備資源分配的調(diào)節(jié)效果,建立了用戶設(shè)備高度聚集的特殊場景,將TPO算法與其他常用算法的處理效果進(jìn)行對比。通過觀察可知,圖6b中傳統(tǒng)的依賴接收信號強(qiáng)度指示(RSSI)進(jìn)行連接的方式會導(dǎo)致MEC服務(wù)器資源分配不合理,進(jìn)而無法滿足用戶需求,圖6c中隨機(jī)法實現(xiàn)的系統(tǒng)設(shè)備發(fā)射總功率為48.3 W,圖6d中TPO算法實現(xiàn)的系統(tǒng)設(shè)備發(fā)射總功率僅為8.7 W,因此隨機(jī)法的實驗結(jié)果不滿足最小化目標(biāo),而本文提出的TPO算法能夠合理有效地建立移動用戶設(shè)備和MEC服務(wù)器的連接,達(dá)到系統(tǒng)設(shè)備發(fā)射總功率優(yōu)化的最優(yōu)效果。

(a)用戶與基站位置 (b)RSSI連接方式

(c)隨機(jī)法連接方式 (d)TPO算法連接方式

4 結(jié) 論

傳統(tǒng)的云計算模型已無法有效解決海量的邊緣數(shù)據(jù)計算卸載問題,如何提升移動邊緣計算的大規(guī)模網(wǎng)絡(luò)架構(gòu)的計算卸載的效率和用戶體驗受到越來越多的關(guān)注。本文在傳輸帶寬和計算資源參數(shù)化的基礎(chǔ)上,使用馬爾可夫近似框架將系統(tǒng)用戶設(shè)備的發(fā)射功率最小化問題轉(zhuǎn)化,設(shè)計分布式的發(fā)射功率優(yōu)化算法求得原目標(biāo)的近似最優(yōu)解。對比基準(zhǔn)算法測試結(jié)果,TPO算法的系統(tǒng)用戶設(shè)備發(fā)射總功率優(yōu)化效果比隨機(jī)法提升了78.5%,同時執(zhí)行效果更加穩(wěn)定;與窮舉搜索的指數(shù)階O(2n)計算復(fù)雜度相比,該算法的復(fù)雜度為線性階O(n),故該算法在有限迭代輪次后即可逼近窮舉搜索的最優(yōu)解;與傳統(tǒng)的RSSI連接方式相比,TPO算法能夠避免在用戶量小范圍高度集中時爭搶計算資源的現(xiàn)象,減少網(wǎng)絡(luò)擁塞和資源分配不均衡的情況發(fā)生,滿足用戶計算卸載需求。TPO算法能夠在保證用戶設(shè)備的時延約束下有效降低系統(tǒng)用戶功耗成本,確保時延敏感型業(yè)務(wù)的時延約束下的用戶體驗。