基于擴張觀測器的輸入受限四旋翼飛行器軌跡跟蹤動態(tài)面輸出反饋控制

沈智鵬,曹曉明

(大連海事大學(xué)船舶電氣工程學(xué)院,遼寧 大連 116026)

0 引 言

四旋翼飛行器具有結(jié)構(gòu)簡單、機動性強和成本低廉等優(yōu)點,在偵察巡邏、影視制作和貨物運輸?shù)葓龊系玫搅藦V泛應(yīng)用。四旋翼系統(tǒng)的強耦合特性和復(fù)雜的動力學(xué)特性使得其模型很難精確建立[1],因此要設(shè)計軌跡精確跟蹤的控制器具有一定挑戰(zhàn)性,而且運動中的飛行器不可避免地受外界擾動的影響,這就進(jìn)一步增加了控制器設(shè)計的難度。

反演法能夠使控制器設(shè)計過程系統(tǒng)化、結(jié)構(gòu)化,且可消除不確定性為匹配條件的限制,因此被廣泛應(yīng)用于非線性系統(tǒng)控制器設(shè)計中。文獻(xiàn)[2]應(yīng)用積分反步法并結(jié)合李雅普諾夫理論設(shè)計控制器,實現(xiàn)四旋翼飛行器軌跡跟蹤控制。傳統(tǒng)反演法在設(shè)計控制器時很容易出現(xiàn)“微分爆炸”問題,為解決這一問題,同時降低算法復(fù)雜度,動態(tài)面技術(shù)[3-5]被應(yīng)用到控制器設(shè)計中。實際工況下,系統(tǒng)未建模動態(tài)和外界未知干擾是難以避免的,采用先進(jìn)算法對其逼近能夠提高系統(tǒng)的魯棒性和控制精度。文獻(xiàn)[6]考慮模型不確定性以及外界干擾的影響,提出一種新型自適應(yīng)軌跡跟蹤控制策略,能夠有效提高飛行器系統(tǒng)的抗干擾能力。文獻(xiàn)[7]針對存在未建模動態(tài)及外部擾動的四旋翼無人機姿態(tài)模型,提出一種自適應(yīng)塊控反演控制方法,設(shè)計控制器同時補償模型動態(tài)不確定和外界擾動,實現(xiàn)軌跡跟蹤控制。文獻(xiàn)[8]把自適應(yīng)反步法與雙積分器李雅普諾夫函數(shù)結(jié)合使用,在控制器設(shè)計同時獲得外界擾動的估計值,保證了在恒定風(fēng)力干擾作用下全局軌跡跟蹤誤差收斂到零。文獻(xiàn)[9]引入擴張狀態(tài)觀測器(extended state observer,ESO)處理飛行器系統(tǒng)模型不確定性以及外界干擾問題,使得飛行器系統(tǒng)對復(fù)合擾動具有較強魯棒性。文獻(xiàn)[10]針對帶有模型參數(shù)不確定和外界擾動的四旋翼系統(tǒng),引入反步法和ESO設(shè)計雙閉環(huán)軌跡跟蹤控制器,使得飛行器系統(tǒng)的魯棒性有了顯著提高。

目前針對擾動未知和模型不確定的四旋翼飛行器控制研究已有豐碩的成果,但同時考慮輸入受限的研究文獻(xiàn)還比較少。由于四旋翼飛行器硬件限制和安全飛行需要,實際控制過程中輸入受限問題是無法避免的。為此,文獻(xiàn)[11]針對四旋翼飛行器偏航控制輸入飽和問題,設(shè)計多模式比例積分微分(multi-mode proportional-integral-derivative,MMPID)控制器抑制執(zhí)行器飽和現(xiàn)象,為系統(tǒng)偏航運動提供保障。文獻(xiàn)[12]針對一類存在控制約束多輸入多輸出(multiple input multiple output,MIMO)非線性系統(tǒng)的軌跡跟蹤問題,提出一種約束自適應(yīng)控制律,并引入輔助系統(tǒng)來減弱輸入約束對系統(tǒng)的影響。文獻(xiàn)[13]針對欠驅(qū)動四旋翼飛行器系統(tǒng)控制輸入受限的軌跡跟蹤控制問題,引入飽和函數(shù)對控制輸出進(jìn)行處理,能夠避免因輸入飽和導(dǎo)致的執(zhí)行器失效問題。以上文獻(xiàn)在進(jìn)行軌跡跟蹤控制時均要求飛行器狀態(tài)信息全部可測,然而在實際飛行過程中一旦傳感器失準(zhǔn)或發(fā)生故障,飛行器的速度信息是不完全可測的。文獻(xiàn)[14]提出了一種具有非匹配模型不確定性的非線性液壓系統(tǒng)輸出反饋控制方法,設(shè)計的ESO用來估計未測量的系統(tǒng)狀態(tài)同時估計模型動態(tài)不確定性。文獻(xiàn)[15]針對一類帶有未知動力學(xué)干擾和隨機擾動的非線性系統(tǒng),設(shè)計ESO,用于估計系統(tǒng)未知狀態(tài)和總干擾信息。文獻(xiàn)[16]針對部分狀態(tài)分量不可測MIMO系統(tǒng)的軌跡跟蹤問題,采用非線性ESO對系統(tǒng)的模型不確定項和未知狀態(tài)進(jìn)行估測,并保證閉環(huán)系統(tǒng)的收斂性。文獻(xiàn)[17]引入不依賴于模型的濾波器估計飛行器的速度信息,以便在速度反饋不可用的情況下完成軌跡跟蹤控制并保證所有閉環(huán)信號有界。

為使所設(shè)計的控制器更加符合實際飛行要求,本文針對速度不可測和控制輸入受限的欠驅(qū)動四旋翼飛行器軌跡跟蹤控制問題,考慮系統(tǒng)存在模型不確定項和未知外部干擾的情況,提出一種基于ESO的輸入受限四旋翼飛行器軌跡跟蹤動態(tài)面輸出反饋控制策略。該策略將四旋翼飛行器模型分解為位置部分和姿態(tài)部分,設(shè)計雙閉環(huán)控制器。引入ESO估測飛行器系統(tǒng)的速度信息同時獲得廣義擾動項,采用動態(tài)面技術(shù)將反演算法中的微分運算轉(zhuǎn)換為簡單且易于實現(xiàn)的代數(shù)運算,并借助雙曲正切函數(shù)設(shè)計動態(tài)補償方程處理輸入飽和問題。最后,以大疆 M100四旋翼飛行器為控制目標(biāo)進(jìn)行軌跡跟蹤控制仿真,驗證所設(shè)計方法的有效性。

1 問題描述

(1)

圖1 四旋翼飛行器模型圖Fig.1 Structure of quadrotor unmanned aerial vehicle

在實際飛行過程中由于電機轉(zhuǎn)速的限制,飛行器控制輸入是有界的,為避免控制量超出此界限,保障飛行安全,引入飽和約束函數(shù)

(2)

(3)

式中,σi為正設(shè)計參數(shù),逼近后產(chǎn)生誤差函數(shù)為

ρ(τj)=sat(τj)-g(τj)

(4)

式中,ρ(τj)為飽和約束函數(shù)與雙曲正切函數(shù)之間的有界誤差項,其界值表示為

|ρ(τj)|=|sat(τj)-g(τj)|=Mi(1-tanh(1))

(5)

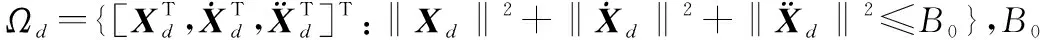
系統(tǒng)控制目標(biāo):針對六自由度欠驅(qū)動四旋翼飛行器模型(1),在滿足假設(shè)1的前提下,考慮系統(tǒng)存在模型動態(tài)不確定和未知外界干擾,以及速度信息不可測和輸入受限的情況。設(shè)計軌跡跟蹤控制器,保證飛行器軌跡跟蹤控制系統(tǒng)中跟蹤誤差信號一致最終有界,實現(xiàn)對飛行器有效的軌跡跟蹤控制。

2 非線性ESO設(shè)計

(6)

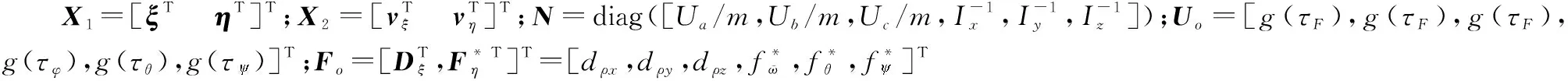
將未建模動態(tài)、氣動干擾等“內(nèi)部擾動”和外界未知干擾等“外部擾動”統(tǒng)稱為廣義擾動。

采用ESO獲得飛行器速度信息,同時對廣義擾動進(jìn)行估測,ESO設(shè)計為

(7)

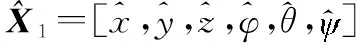
(8)

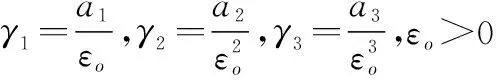
(9)

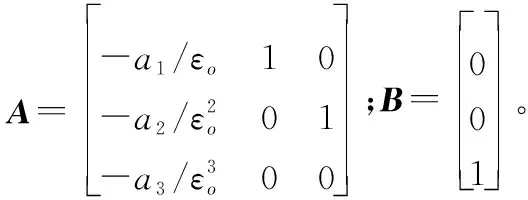
(10)

式中,c1,c2,c3均為正實數(shù)且互不相等,對于矩陣A,存在范德蒙德矩陣Q滿足

(11)

定義cmin=min{c1,c2,c3} ,求解式(9)可得

(12)

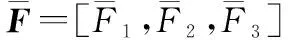
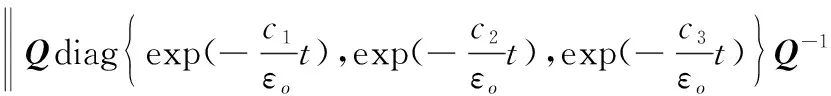
(13)

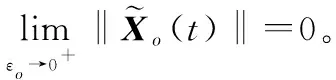
證畢

本文在式(7)的基礎(chǔ)上引入非線性函數(shù)fal(·),設(shè)計非線性ESO為

(14)

非線性函數(shù)fal(·)表示形式[16]為

(15)

3 輸出反饋控制器設(shè)計

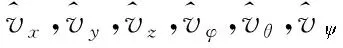
3.1 位置環(huán)控制器設(shè)計

定義位置誤差為

(16)

式中,xd,yd,zd為參考軌跡。

定義線速度誤差為

(17)

式中,αi(i=1,2,3)為待設(shè)計的虛擬控制量。

為了降低飽和效應(yīng),減小輸入受限對系統(tǒng)狀態(tài)跟蹤誤差的影響,引入輔助系統(tǒng)對跟蹤誤差e23進(jìn)行補償,輔助系統(tǒng)設(shè)計為

(18)

式中,κ1>0為設(shè)計參數(shù);hξ為輔助系統(tǒng)狀態(tài);Uc/m為飛行器系統(tǒng)模型中的非線性部分。

重新定義補償修正后的跟蹤誤差為

(19)

選取Lyapunov函數(shù)V1為

(20)

對V1求導(dǎo)并結(jié)合式(16)和式(17)整理得

(21)

根據(jù)式(21)借助逆推法設(shè)計虛擬控制律為

(22)

式中,λ1i>0(i=1,2,3)為設(shè)計參數(shù)。

(23)

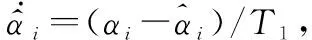
(24)

選取Lyapunov函數(shù)V2為

(25)

對V2求導(dǎo)并結(jié)合式(1)和式(17)整理得

(26)

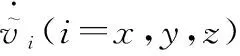
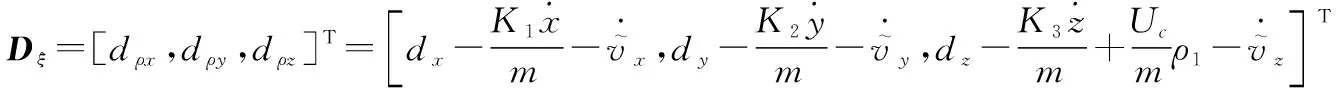
(27)

考慮方程

(28)

經(jīng)運算可得

(29)

考慮實際工況下四旋翼安全飛行的需要,對俯仰角與滾轉(zhuǎn)角范圍給出約束條件為

|φ|≤φmax,|θ|≤θmax

(30)

為方便說明,進(jìn)行變量代換，即

(31)

約束條件中,兩個參數(shù)φmax,θmax均在(0,π/2)內(nèi)取值,整理得到俯仰角和滾轉(zhuǎn)角指令信號為

(32)

3.2 姿態(tài)環(huán)控制器設(shè)計

將式(1)模型中姿態(tài)部分轉(zhuǎn)化為

(33)

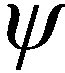
定義姿態(tài)誤差為

(34)

定義角速度誤差為

(35)

引入輔助系統(tǒng)對跟蹤誤差e4進(jìn)行補償,輔助系統(tǒng)設(shè)計為

(36)

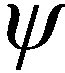
重新定義補償修正后的跟蹤誤差

(37)

選取Lyapunov函數(shù)V3為

(38)

對V3求導(dǎo)并結(jié)合式(34)和式(35)整理得

(39)

設(shè)計虛擬控制律為

(40)

式中,λ3>0為設(shè)計參數(shù)。

(41)

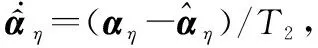
(42)

選取Lyapunov函數(shù)V4為

(43)

對V4求導(dǎo)并結(jié)合式(33)和式(37)整理得

(44)

(45)

文獻(xiàn)[9-10]在控制器設(shè)計過程中未考慮控制輸入受限問題,但在實際工程中,控制輸入飽和[22]現(xiàn)象是無法避免的。本文引入飽和約束函數(shù),消除了因輸入飽和導(dǎo)致的執(zhí)行器失效現(xiàn)象,并設(shè)計輔助補償系統(tǒng)以降低飽和效應(yīng)。

文獻(xiàn)[13]在控制器設(shè)計過程中未考慮狀態(tài)信息不可測的情況,但特殊工況下因傳感器失效導(dǎo)致飛行器速度信息不可測也是在所難免的。本文引入ESO對系統(tǒng)速度進(jìn)行估測,能夠有效應(yīng)對傳感器失效或者失準(zhǔn)的狀況,提高系統(tǒng)穩(wěn)定性能。

4 穩(wěn)定性分析

選取Lyapunov函數(shù)為

(46)

對Vc求導(dǎo)并結(jié)合式(26)和式(44)整理得

(47)

(48)

繼續(xù)整理式(47)可得

(49)

其中

(50)

(51)

(52)

解不等式(49),可得

(53)

可得

(54)

5 仿真分析

為驗證本文所設(shè)計輸入受限四旋翼飛行器軌跡跟蹤動態(tài)面輸出反饋控制器的有效性,以大疆 M100飛行器為對象,分別采用螺旋盤升指令和矩形指令進(jìn)行仿真驗證,飛行器模型參數(shù)如表1所示。

表1 大疆 M100模型參數(shù)Table 1 DJI M100 model parameters

四旋翼飛行器模型不確定部分設(shè)定為

四旋翼飛行器受到的外界干擾設(shè)為

控制器參數(shù)選取λ1i=2(i=1,2,3),λ2i=8(i=1,2,3),λ3=6,λ4=36,T1=0.01,T2=0.01,ESO參數(shù)取γ1=60,γ2=600,γ3=6 000,飽和輔助系統(tǒng)參數(shù)取κ1=3,κ2=3,σi=2(i=1,…,4),控制輸入界限取[M1,M2,M3,M4]=[50,10,10,2]。

設(shè)定飛行器的初始位置和狀態(tài)信息為

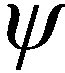
5.1 螺旋盤升軌跡跟蹤仿真

螺旋盤升軌跡設(shè)定為

圖2為本文算法控制下四旋翼飛行器跟蹤螺旋盤升軌跡仿真曲線。

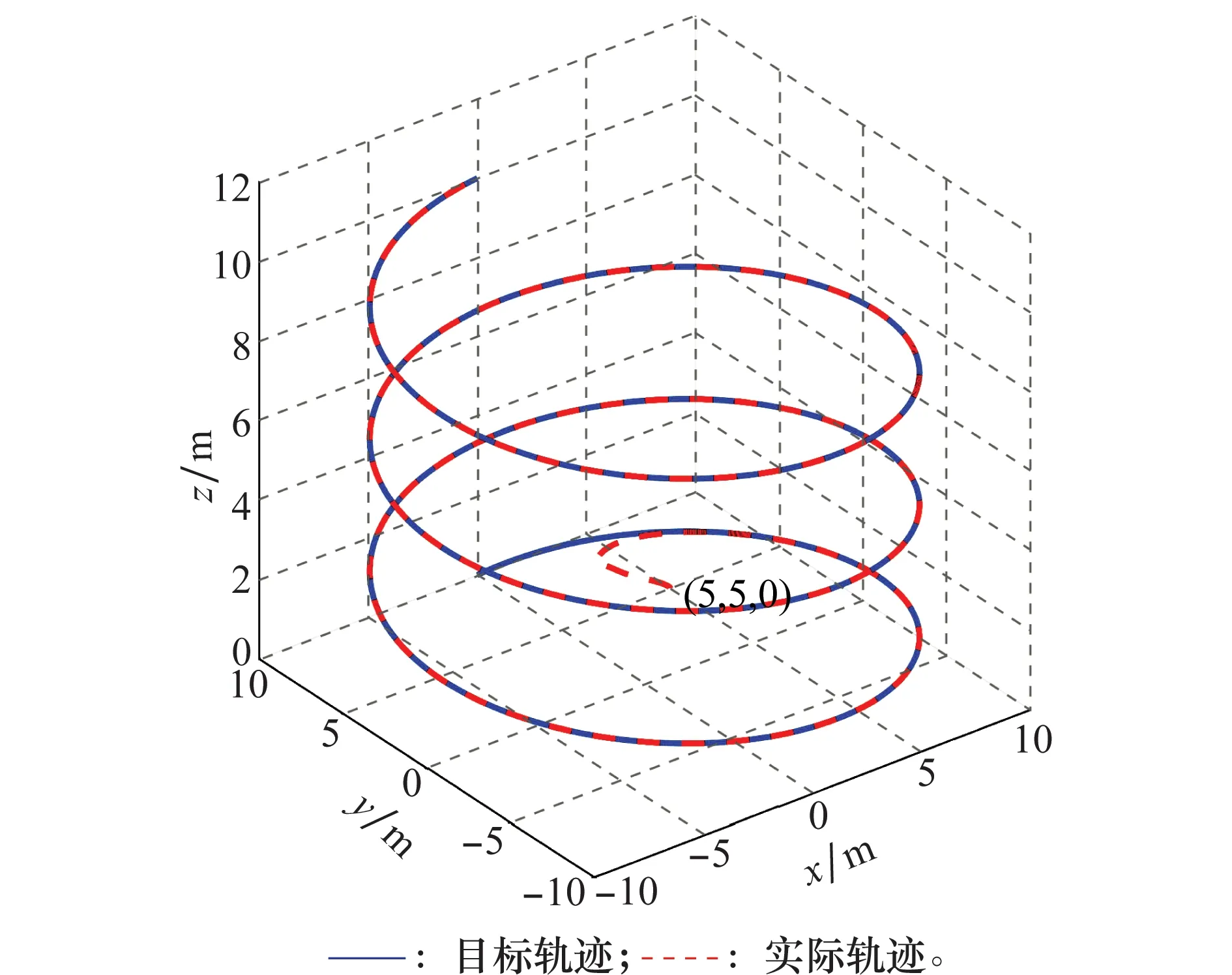
圖2 四旋翼飛行器軌跡跟蹤曲線Fig.2 Curves of quadrotor unmanned aerial vehicle trajectory tracking

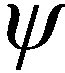
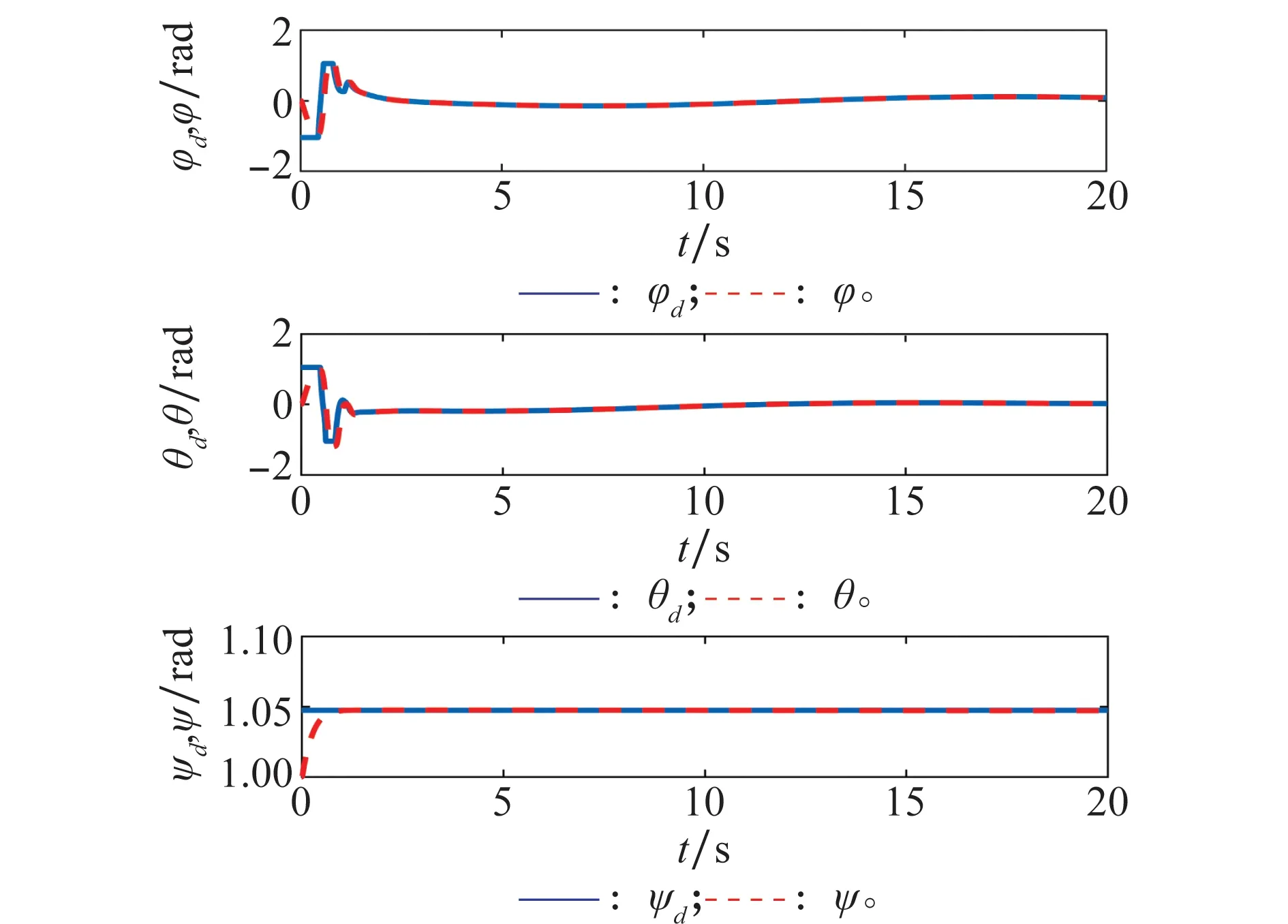
圖3 四旋翼飛行器姿態(tài)角度跟蹤曲線Fig.3 Curves of quadrotor unmanned aerial vehicle attitude angles tracking

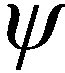
圖4 軌跡和姿態(tài)角度跟蹤誤差曲線Fig.4 Curves of trajectory and attitude angles tracking errors

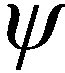
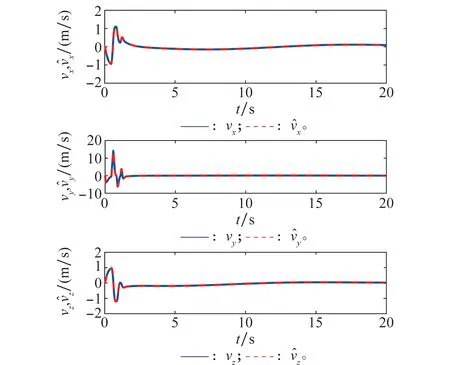
圖5 觀測器估測線速度歷時曲線Fig.5 Curves of translational velocity observation versus time

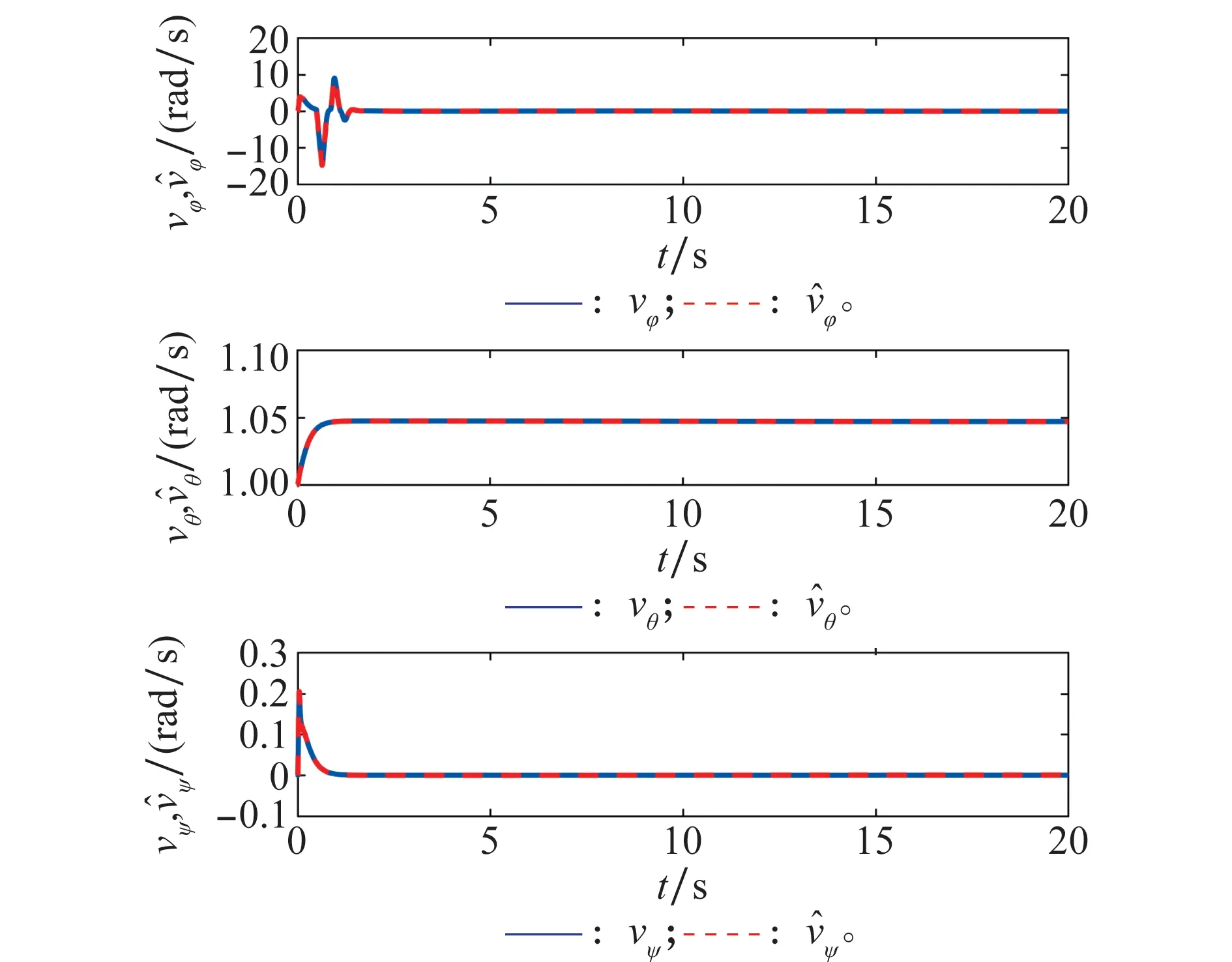
圖6 觀測器估測角速度歷時曲線Fig.6 Curves of angular velocity observation versus time

圖7和圖8分別為位置部分和姿態(tài)部分廣義擾動觀測曲線,可見ESO可以準(zhǔn)確地觀測出廣義擾動,從而有效地提高飛行器軌跡跟蹤控制精度和魯棒性。

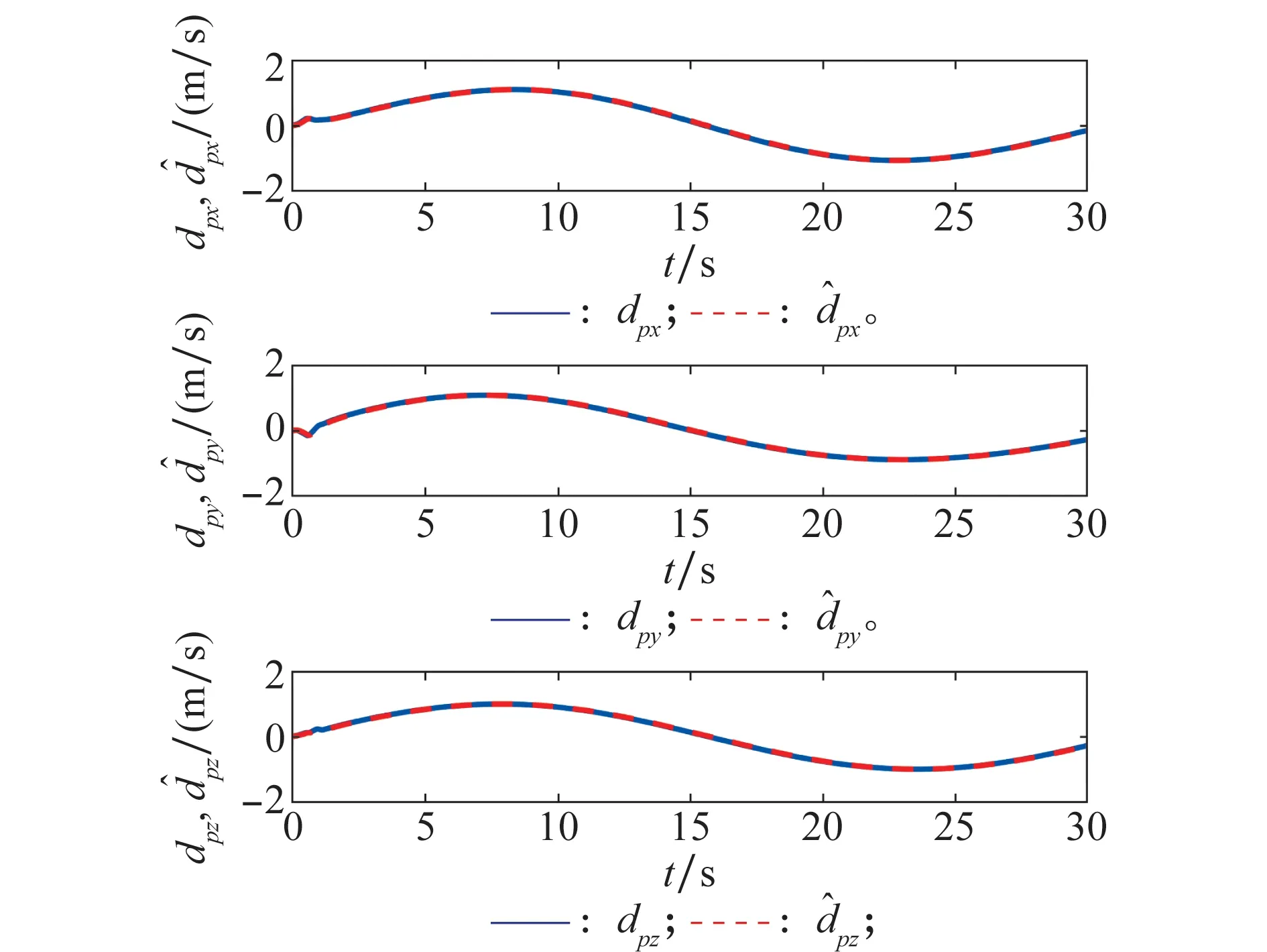
圖7 位置部分廣義擾動觀測曲線Fig.7 Curves of position’s generalized disturbances observation

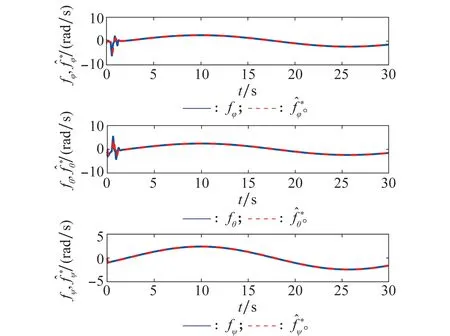
圖8 姿態(tài)部分廣義擾動觀測曲線Fig.8 Curves of attitude’s generalized disturbances observation

圖9為升力和力矩曲線,τj表示系統(tǒng)控制輸出,g(τj)表示執(zhí)行器輸入。

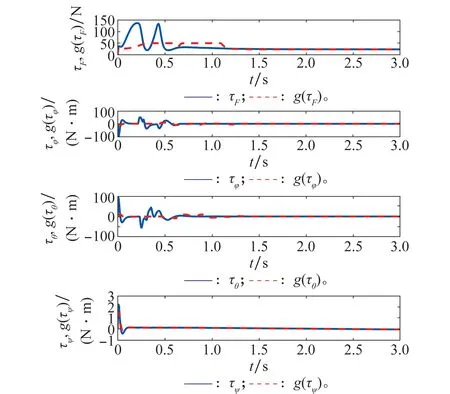
圖9 升力和力矩曲線Fig.9 Curves of thrust and torque

分析圖9可知飛行器控制輸出τj在0～0.8 s幅值明顯超出執(zhí)行器可執(zhí)行范圍,經(jīng)本文帶有誤差補償?shù)南拗撇呗院?執(zhí)行器輸入g(τj)的幅值被限定在安全范圍之內(nèi),同時飽和補償項實時對跟蹤誤差進(jìn)行受限補償,有效避免了控制輸入飽和引起的飛行器失控,能夠為飛行器提供更加安全可靠的控制量。

5.2 矩形軌跡跟蹤仿真

矩形軌跡設(shè)定為

xd=10{[tanh(t-10)-tanh(t-30)]/2}

yd=10{[tanh(t-20)-tanh(t-40)]/2}

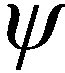
圖10為矩形軌跡跟蹤曲線,從圖10中可以看出經(jīng)3 s左右時間飛行器從起飛點(5,5,0)處快速準(zhǔn)確地到達(dá)預(yù)定軌跡的起始點(0,0,2)處并沿預(yù)定矩形軌跡飛行。

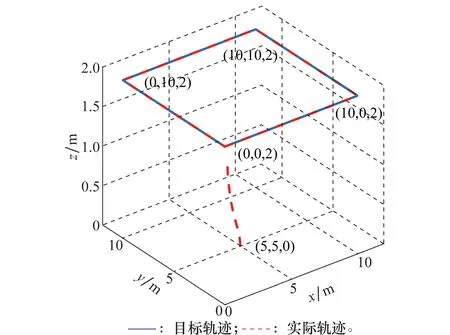
圖10 四旋翼飛行器矩形軌跡跟蹤曲線Fig.10 Curves of quadrotor unmanned aerial vehicle rectangular trajectory tracking

圖11為軌跡和姿態(tài)角度跟蹤誤差曲線,顯然在5 s之前誤差快速收斂,并在本文設(shè)定的相對復(fù)雜的工況下保持較高的跟蹤精度。

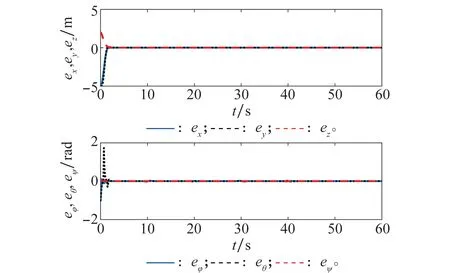
圖11 軌跡和姿態(tài)角度跟蹤誤差曲線Fig.11 Curves of trajectory and attitude angles tracking errors

圖12為升力和力矩曲線,由0～3 s仿真數(shù)據(jù)可知控制量在3 s左右達(dá)到平穩(wěn)狀態(tài),由3～45 s仿真曲線可以看出在10 s,20 s,30 s,40 s這些需要飛行器狀態(tài)做出較大調(diào)整的時刻,控制器可以很快做出調(diào)整并迅速恢復(fù)平穩(wěn),并且經(jīng)本文限制策略后,幅值限定在給定的界值范圍之內(nèi),說明本文設(shè)計的帶有限制函數(shù)和補償策略的執(zhí)行輸入能夠有效應(yīng)對控制飽和問題。

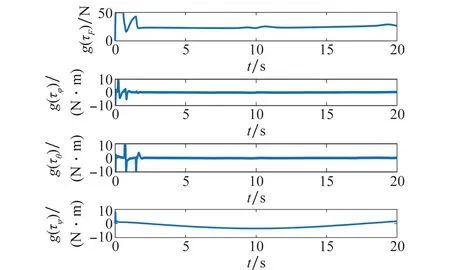
圖12 升力和力矩曲線Fig.12 Curves of thrust and torque

6 結(jié) 論

針對六自由度四旋翼飛行器存在模型不確定性、外界未知干擾、速度不可測和輸入受限等情況,構(gòu)造ESO估測飛行器速度信息和廣義擾動。引入反演法和動態(tài)面技術(shù),設(shè)計基于ESO的輸入受限四旋翼飛行器軌跡跟蹤輸出反饋控制器。以大疆 M100為被控對象分圓形軌跡和矩形軌跡兩種情況進(jìn)行軌跡跟蹤仿真。結(jié)果表明,本文所述方法對模型不確定性和復(fù)合擾動表現(xiàn)出較強的魯棒性,同時能夠有效應(yīng)對速度不可測的情況,解決了因輸入飽和限制導(dǎo)致的控制輸出不穩(wěn)定問題,對工程實踐具有一定的指導(dǎo)意義。