隨機沖擊影響的非線性退化設備剩余壽命預測

白 燦,胡昌華,司小勝,李洪鵬,張正新,裴 洪

(1.火箭軍工程大學測試教研室,陜西 西安 710025;2.北京遙感設備研究所,北京 100854)

0 引 言

航天工業設備通常由于其材料性能的內在變化與工作環境的相互作用而發生性能退化,因而需要時刻關注表征設備健康狀態的各項性能指標,一旦設備的性能無法得到有效評估,設備將會面臨失效的風險。設備的意外失效會造成不同程度的經濟損失和環境破壞。如果在設備失效之前能夠對其壽命或剩余使用壽命進行有效的估算,則相應的序貫決策活動將被安排,以避免災難性事故,從而達到降低成本和保護環境的目的。在實際中,傳統的基于統計分析的壽命預測方法往往需要獲得足夠的壽命數據,然而這類方法對于壽命長或高成本的航天類設備難以適用。近十年來狀態監測(condition monitor,CM)技術的快速發展使得收集足夠的退化數據用以揭示設備的健康狀況成為可能,進一步促進了基于退化建模方法的迅速發展[1-2]。

經過幾十年的發展,當前設備剩余壽命(remaining useful life,RUL)預測方法已有相當豐碩的成果。文獻[3]在對設備數據采集和RUL預測的系統性綜述中,總結回顧了前人的研究成果,將RUL預測方法分為基于物理模型的方法、數據驅動的方法以及混合方法。由于現代設備的復雜性,其內部零部件退化機制難以掌握,這極大地增加了采用物理模型的方法進行RUL預測的難度。數據驅動的方法能有效回避這個問題。該方法是將目標設備退化過程中測試得到的有效退化數據用于相應的退化模型中進行RUL預測,近些年來在壽命預測領域中備受青睞。文獻[4]將數據驅動的方法分為基于隨機過程的方法、人工智能的方法、隨機系數回歸的方法以及比例風險模型的方法,其中基于隨機過程的方法使用的最為頻繁。隨機過程一般包括Wiener過程[5]、Gamma過程[6]、Markov鏈[7]以及逆高斯過程[8]。Wiener過程是一類具有高斯獨立分布增量的隨機過程,與其他隨機過程相比,更便于描述非嚴格單調的退化過程,有利于進行參數估計和求解RUL分布的解析解。也正因其諸多優良的特性受到了國內外學者們的青睞,故本文以Wiener過程為基礎進行退化建模。

實際工程中,設備除了經歷正常退化之外,還會不同程度的受到一些外界環境因素(轉運、沖擊、腐蝕等)的影響。而這些因素可以看做一種廣義上的隨機沖擊,對設備退化水平會造成額外的影響。文獻[9]考慮了沖擊對退化過程的影響,基于多狀態模型研究了系統可靠性。文獻[10]考慮了極端沖擊效應與故障率之間的關系,基于Brown-proschan模型得到了系統可靠性分布。文獻[11]基于離線評估模型,分別考慮了兩種沖擊模型下的可靠性研究。文獻[12]考慮到隨機沖擊導致的軟、硬失效影響,基于競爭失效過程對單部件系統可靠性以及維修管理問題開展研究。文獻[13-15]基于線性退化隨機過程建立多部件系統退化模型,考慮沖擊與退化的相關性分別得到系統可靠性函數并提出相應的維修決策。文獻[16]分析了沖擊效應在軟、硬失效過程中的作用情況,并采用粒子濾波方法得到了RUL的點估計。文獻[17]將沖擊損傷刻畫為已知的固定常數,推導出線性退化情況下的設備RUL概率密度函數(probability density function,PDF)表達式。從上述文獻出可以看出,盡管沖擊與退化過程已有相當的研究工作,但在壽命預測領域仍缺乏較好的研究方法,比如如何考慮沖擊效應對非線性退化過程壽命預測的影響,如何推導RUL PDF解析解等。針對上述問題,本文基于非線性Wiener過程,考慮了累積型隨機沖擊的影響,建立了一種退化沖擊模型。將沖擊效應刻畫為未知的正態分布變量,根據首達時間(first hitting time,FHT)概念,提出一種壽命和RUL PDF近似解析表達式,極大地縮短了計算時間。基于歷史CM數據,采用期望最大化(expectation maximum,EM)算法進行參數估計。通過數值仿真說明隨機沖擊對壽命預測精度的影響,并采用航天鋰電池退化實例對本文所提壽命預測方法的有效性進行驗證。

1 退化建模和壽命預測

1.1 隨機沖擊退化設備建模

將存在隨機沖擊影響下的設備退化過程反映在圖1中。

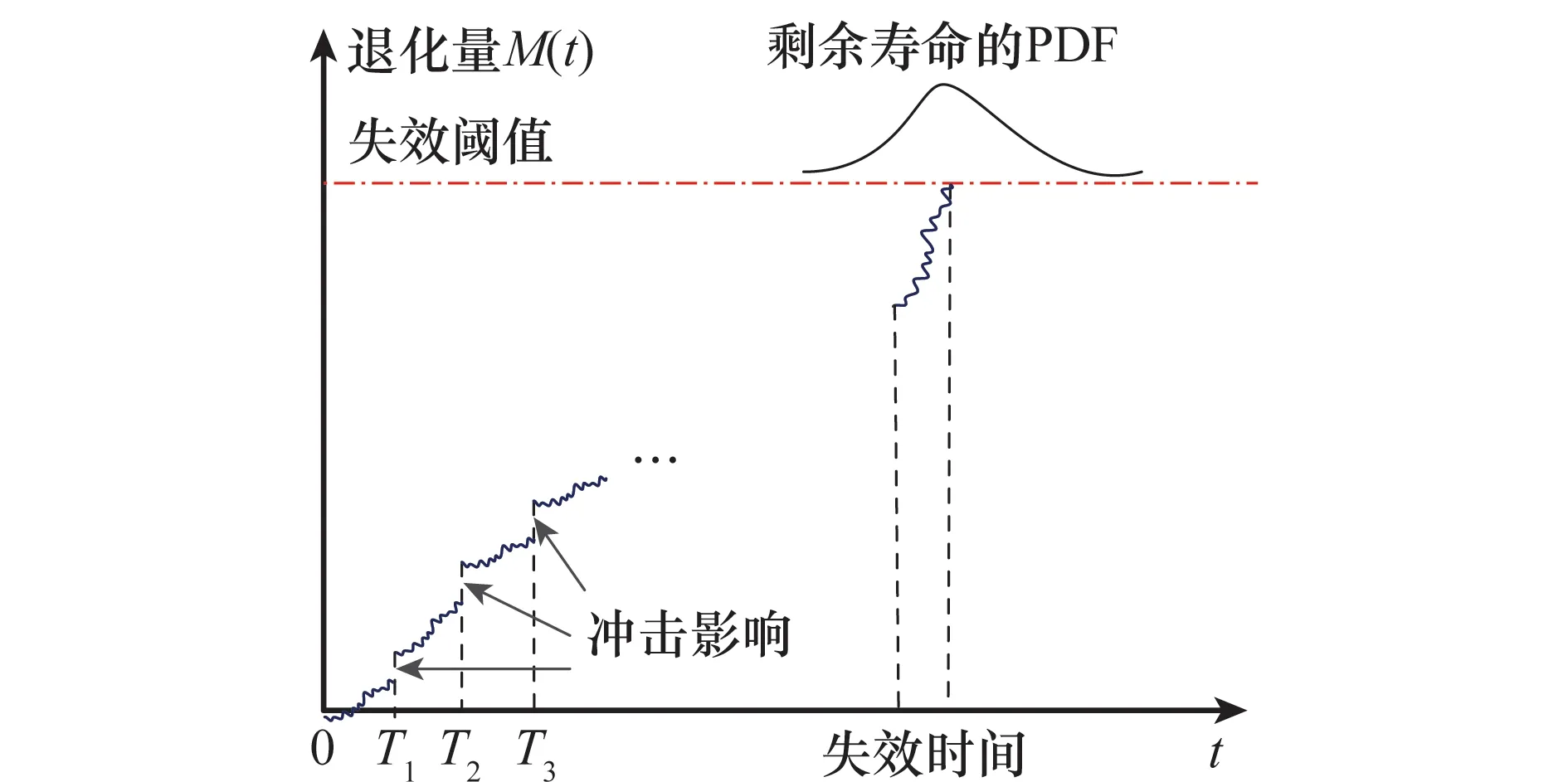
圖1 隨機沖擊影響下的設備退化軌跡Fig.1 Equipment degradation trajectory with random shocks

圖1中橫坐標t代表時間推移,縱坐標代表t時刻設備的退化水平{M(t),t≥0}。ω為失效閾值。T1、T2、T3…是隨機沖擊發生的時刻。當退化量達到既定的失效閾值ω時,認定設備發生失效。值得注意的是,在本文研究中,設備經歷沖擊的時間不計入壽命周期。

用隨機過程{M(t),t≥0}刻畫設備的退化過程。考慮受到隨機沖擊帶來的影響,設備在t時刻的實際退化過程應該由以下兩部分的綜合:t時刻設備的正常退化和t時刻之前所經歷的隨機沖擊活動的影響。通過一個退化軌跡隨時間遞增的退化過程,設備在t時刻的退化模型為

M(t)=X(t)+S(t)

(1)

(2)

(3)

1.2 壽命及RUL PDF

求解tk時刻RULLk的PDF關鍵是推導tk時刻壽命T的PDF。采用FHT的概念,模型所刻畫的退化設備壽命T和RULLk可以分別定義為

T=inf{M(t)≥ω|M(0)<ω}

(4)

Lk=inf{lk:M(lk+tk)≥ω|M(tk)<ω}

(5)

式中,X(tk)為tk時刻的退化量。針對非線性退化設備,不考慮沖擊影響時,根據參考文獻[18]中的定理2,可分別得到tk時刻壽命T和tk時刻RULLk的分布,對應的PDF分別為

(6)

fLk|θu(lk|θu)=

(7)

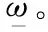
引理1若Z～N(u,σ2),且ω1,ω2,A,B∈R,C∈R+,則有

(8)

因此,基于全概率準則,結合引理1及式(6)和式(7),隨機退化過程{M(t),t≥0}相對應的壽命T和RULLk的PDF可以分別表示為

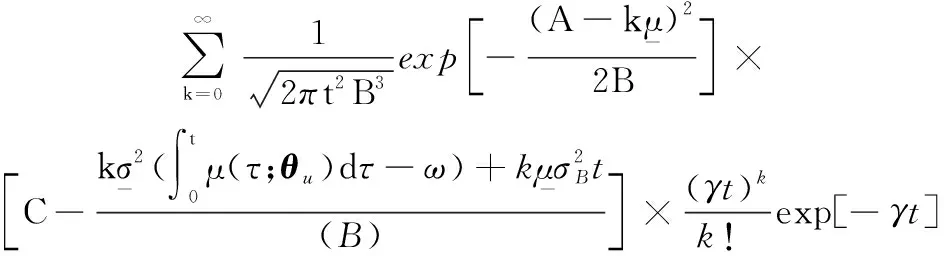
(9)

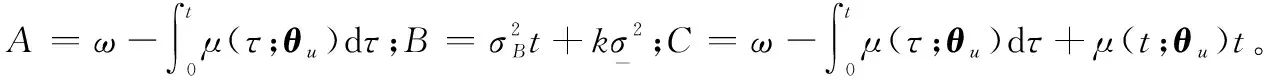
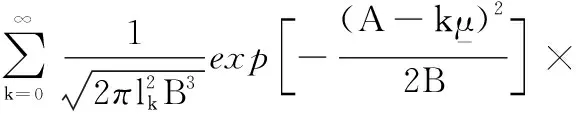
(10)

可以發現,式(9)和式(10)考慮了在預測區間內存在無數次隨機沖擊的情況,這種計算方法將導致計算速度過慢的問題,耗費時間過長。工程實際上,通常需要對隨機沖擊出現的次數進行合理截斷,忽略出現概率小的情況。因此,式(9)和式(10)很少被應用于根據實時的壽命及RUL預測結果作出相應的健康管理決定。

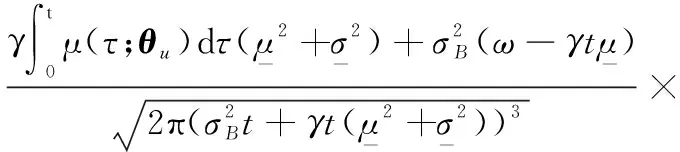
(11)

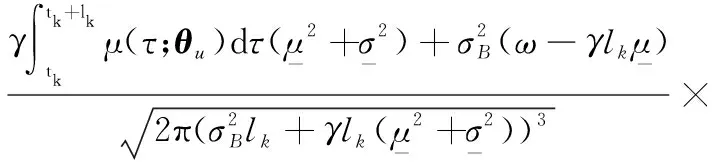
(12)

2 參數估計

(Δmi|θ2)

(13)

f1(Δmi|θ1)=

(14)

(15)

EM算法中,在E步驟基于第l步的重復估計結果計算第(l+1)步時隱含變量Z的期望。記為

(16)

經過l次重復計算,在M步驟中,為得到(l+1)次的參數結果,將條件似然函數極大化。得到(l+1)步時估計的參數為

(17)

(18)

(19)

(20)

(21)

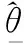
3 數值仿真

表1 仿真參數設定Table 1 Simulation parameter setting

圖2 不同值時壽命分布PDF和直方圖Fig.2 PDF and histogram of life distribution under different

圖3 不同值時壽命分布PDF和直方圖Fig.3 PDF and histogram of life distribution under different

圖4 不同γ值時壽命分布PDF和直方圖Fig.4 PDF and histogram of life distribution under different γ

4 實例驗證

將本文所提方法應用于分析鋰離子電池的容量退化現象。采用美國國家航天局阿姆斯研究中心公開的鋰電池數據[22]。對于鋰離子電池,剩余容量隨著充/放電操作循環次數增加而降低,其被廣泛應用于描述長期退化[23]。在壽命周期中,由于充/放電循環的中止,電池在沒有電子壓力的情況下一段時間容量會有所恢復。這種容量的恢復可認為是經過處理的負的隨機沖擊增加到退化過程中。從公開數據中選取B18,B5,B7 3種型號電池作為本文模型和算法的驗證。將3種型號電池依次編號為#001,#002,#003。研究表明,25%的原始容量損失將導致鋰離子電池失去提供達到要求電源的能力,故失效閾值設置為0.25。轉換后的退化數據繪制在圖5中,由此看出3組電池退化軌跡為非線性,且符合冪次函數形式。

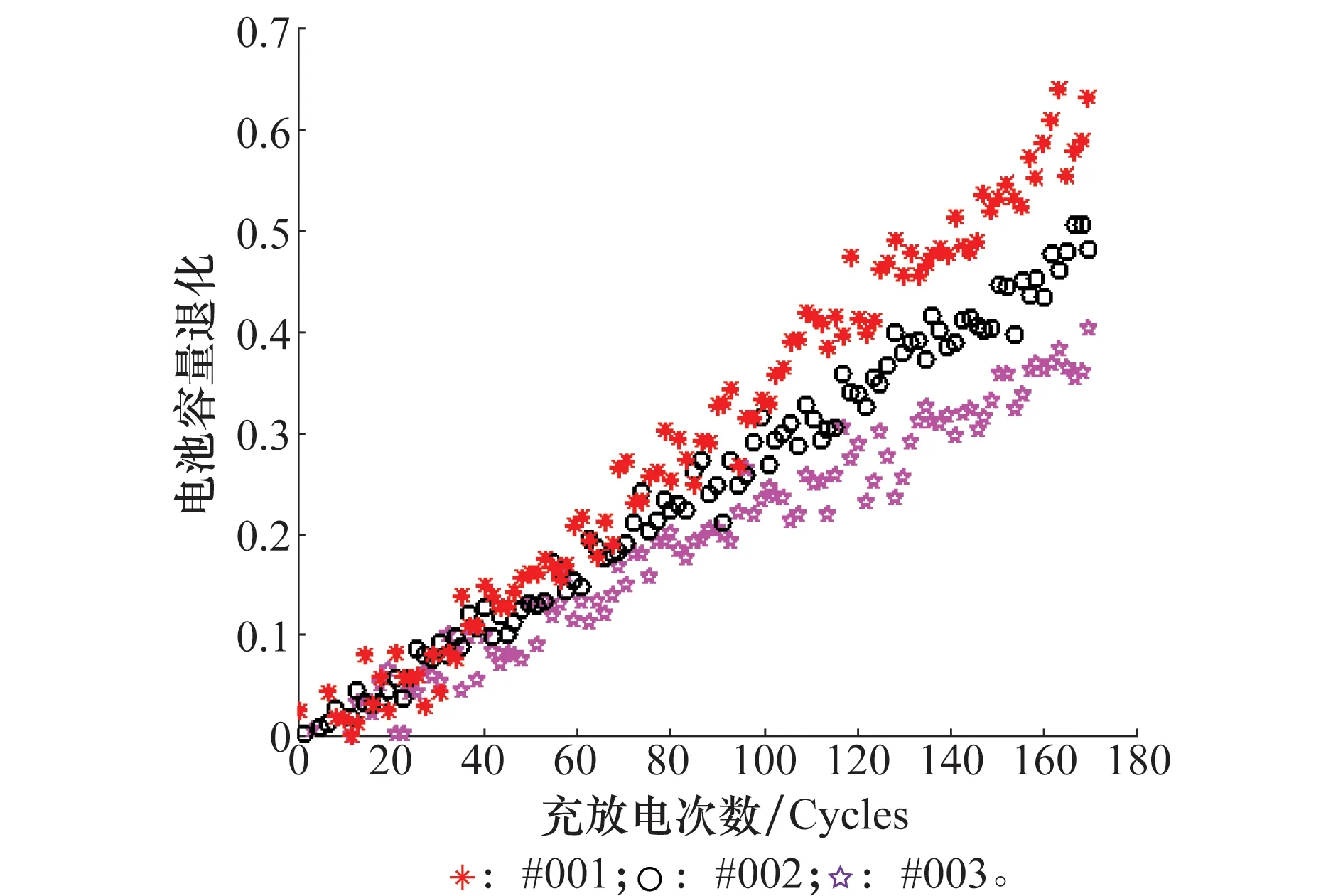
圖5 3組型號鋰電池容量退化Fig.5 Capacity loss of the three lithium batteries

根據本文所提方法,對每個退化電池進行參數估計。3種電池真實充/放電循環次數分別為99、126、160。相應的,采用本文方法預測出的壽命分別為86、128、164。對應的預測壽命相對誤差分別為13.13%、1.58%、2.50%。壽命預測和參數估計該結果分別表示在圖6和表2中。

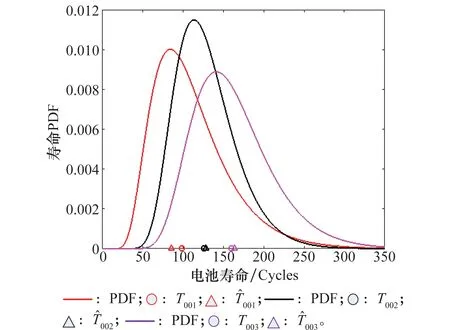
圖6 不同退化電池壽命PDF預測Fig.6 PDF prediction of different degradation batteries

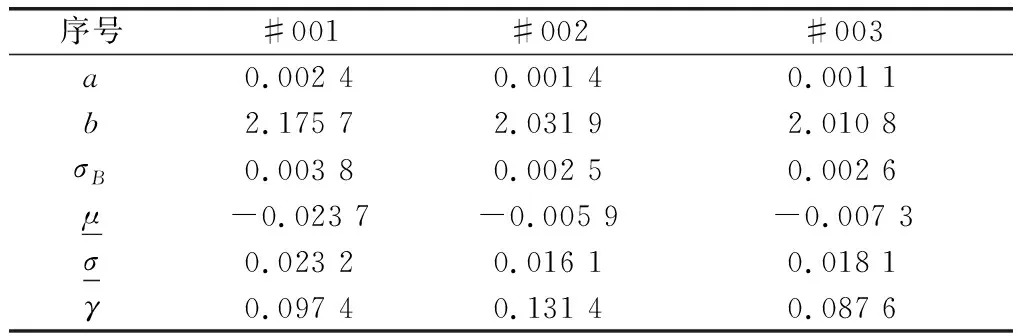
表2 參數估計結果Table 2 Parameter estimation result

圖6中圓形代表實際壽命,三角形代表預測壽命。這些結果表明,本文所提方法可以實現有效的鋰電池壽命預測。此外,#003號電池容量退化數據用于驗證本文所提出的剩余壽命方法,RUL PDF從16循環至144循環每隔16個循環顯示在圖7中,同時與圖8中未考慮沖擊影響的RUL預測結果進行比較,說明了在鋰電池容量退化過程中,考慮隨機沖擊影響顯著提高了RUL預測精度。

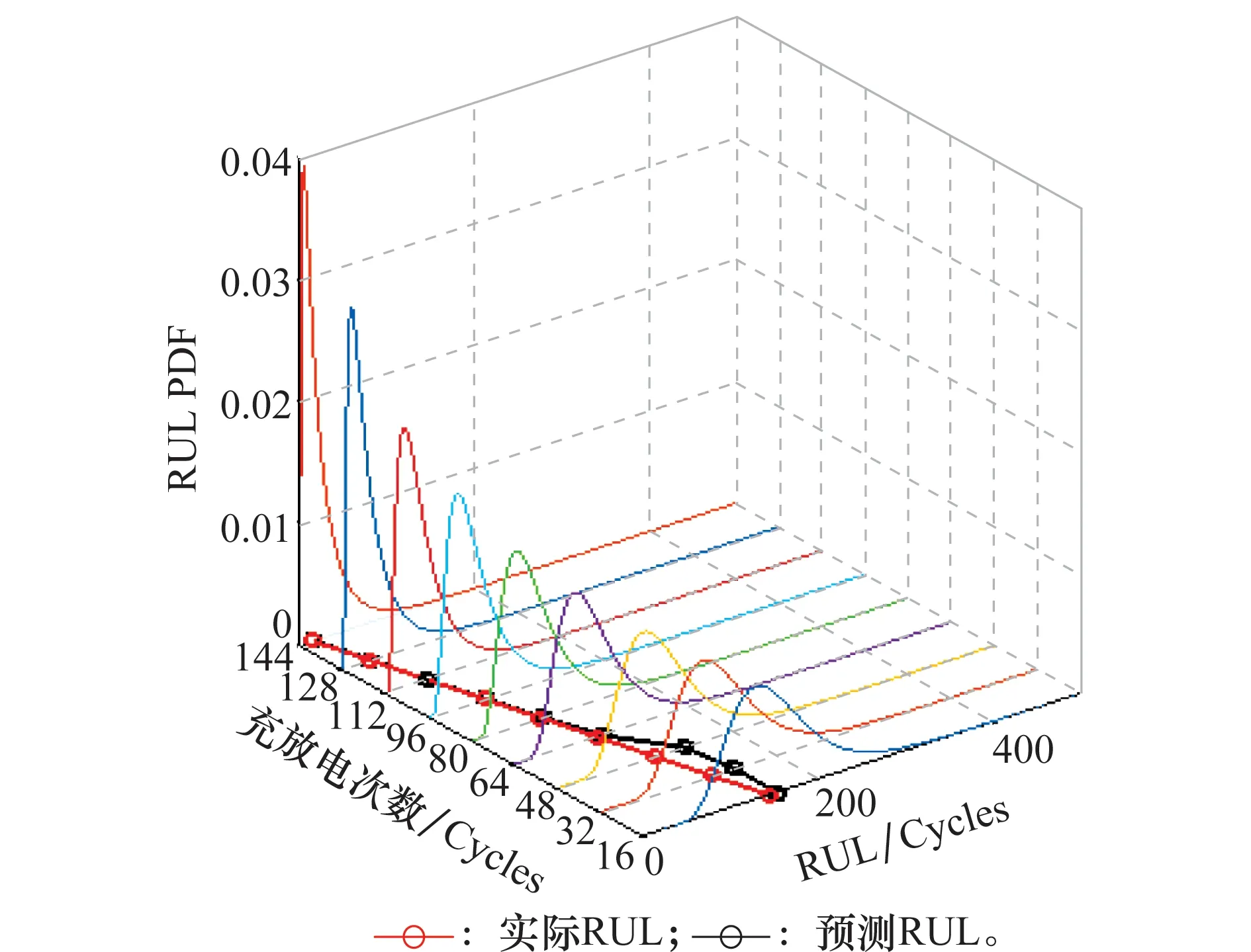
圖7 #003號電池考慮沖擊影響RUL預測Fig.7 RUL prediction with shocks of #003 batteries

圖8 #003號電池不考慮沖擊影響RUL預測Fig.8 RUL prediction without shocks of #003 batteries

最后,根據考慮沖擊時的RUL預測均方值誤差(mean squared error,MSE)說明該方法的有效性,如圖9所示。

(22)

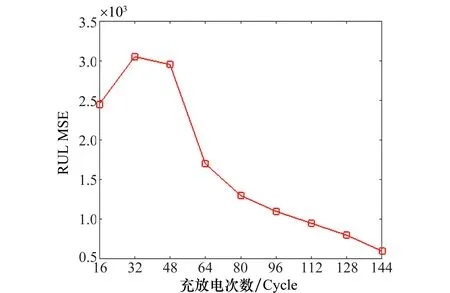
圖9 #003號電池RUL MSEFig.9 Mean squared error of #003 batteries RUL

通過式(22)能夠確定在各采樣時刻的均方誤差。從圖9可以觀察到隨著充/放電循環次數增加,MSE值減小,表明RUL預測更加精確。

5 結 論

本文以Wiener過程為基礎,重點分析了存在累積型隨機沖擊影響下的非線性退化設備RUL預測問題。通過一個復合Poisson的過程描述隨機沖擊對退化的影響,基于首達時間概念求出非線性退化情況下壽命和RUL PDF理論和近似解析表達式,避免了數值計算量大的問題。通過EM算法利用歷史退化數據進行參數估計,確定了退化模型中的未知參數。數值仿真實驗說明隨機沖擊對壽命預測分布均值以及方差造成的具體影響。采用航天鋰離子電池的一個實例研究驗證本文所提的方法的有效性。本文研究內容可以為使用中存在隨機沖擊影響下的設備壽命預測和健康管理提供一定的理論基礎,體現了一定的工程應用價值。