基于即時修復式稀疏A*算法的動態航跡規劃
王生印,龍 騰,王 祝,蔡祺生
(1.北京理工大學宇航學院,北京 100081;2.飛行器動力學與控制教育部重點實驗室,北京 100081)
0 引 言
在復雜多變的真實環境中,往往存在著突發、移動威脅和機動目標,無人機必須對環境變化做出快速反應,在規定時間范圍內即時規劃出新的可行航跡以保證無人機飛行安全,同時盡可能提高航跡最優性以減小無人機能量消耗和提高任務效能。
目前,無人機航跡規劃方法主要包括智能優化算法[1-5]和圖搜索算法[6-9]等。其中,智能優化算法由于其計算量隨問題維數呈指數增長,難以在復雜環境下規劃出可行航跡[10]。而以稀疏A*搜索(sparse A*search,SAS)算法[11-14]為代表的啟發式圖搜索算法因其效率高和魯棒性強等優點,在工程上應用最為廣泛。但SAS算法的規劃時間會隨著規劃環境復雜程度的增大而增長,并容易陷入局部搜索,難以滿足動態航跡規劃的快速性需求。快速擴展隨機樹算法[15-18]通過引入隨機采樣能夠有效避免算法陷入局部搜索的缺陷,快速找到一條可行航跡,但算法的隨機性導致規劃結果穩定性差,而且最優性難以滿足實際應用需求。
針對復雜動態環境中傳統航跡規劃算法難以穩定地在規定時間內生成較優航跡的問題,國內外學者開展了基于即時架構的搜索算法研究[19-28]。即時搜索算法族可以在規劃開始后的任意時刻輸出當前搜索到的最優規劃結果[29],并且隨著計算時間的增加通過循環規劃的方式使航跡質量不斷提升,實現了規劃時效性和結果最優性之間的合理權衡,能夠有效處理動態航跡規劃問題。
即時搜索架構主要包括權重式、窗口式和修復式[19-20,22]。文獻[20]提出了加權式即時A*算法,該算法能夠在較大的啟發權重下快速找到初始解,并通過后續不斷重復擴展具有局部不一致性的節點以尋找更優解。文獻[19]提出了窗口式即時A*算法,通過設置窗口大小從而限制擴展節點的數目,使得只有在窗口內的節點才能加入擴展;當初始窗口為0時,該方法退化為深度優先搜索算法,在復雜環境下可能錯失可行解,并且隨著窗口的增大后續的搜索效率也逐漸降低。文獻[22]提出了即時修復式A*(anytime repairing A*,ARA*)算法,通過逐次減小啟發項權重多次執行加權A*算法,以獲得更優的規劃結果;ARA*算法能夠在每一次迭代過程中利用以往的擴展信息提高后續搜索效率。
文獻[25]對修復式、權重式和重啟式3種即時搜索架構進行了分析和對比,結果表明即時修復式構架能夠更快地收斂到最優解,并且針對不同的搜索算例具有更強的魯棒性。但是該架構需要依賴很小的啟發項權重才能獲得最優解[13],該特點降低了算法節點擴展的效率。此外,現有的即時A*算法主要針對機器人和機械臂規劃問題[21,23],無法直接應用于無人機航跡規劃。
本文基于無人機動態航跡規劃的需求,將即時修復式構架與SAS相結合,并針對即時修復式構架中低啟發項偏好缺陷和算法效率對規劃區域和障礙尺度強烈敏感的問題進行改進,引入雙排序準則、存儲空間約束及變步長策略,提出了即時修復式稀疏A*搜索(anytime repairing SAS,AR-SAS)算法。靜態環境下蒙特卡羅仿真結果表明AR-SAS算法生成可行航跡與最優航跡的時間都小于分層SAS算法[12,14]和標準SAS算法[26]。同時,動態環境仿真結果表明,AR-SAS算法能夠快速規劃出較優的可行航跡,具有較高的規劃效率和較強的魯棒性,滿足無人機動態航跡規劃的需求。
1 航跡規劃問題建模
無人機航跡規劃需綜合考慮地形、氣象、障礙等環境因素以及平臺自身的飛行性能約束,為無人機制定出從初始位置到目標位置的最優飛行路徑[27,30]。
記無人機三維空間內位置為(x,y,z),其中x、y表示東向和北向位置坐標,z表示海拔高度。無人機航跡通過一組節點序列{Sstart,S1,…,Sn-1,G}來表示,其中Sstart為起始點,G為目標點,S1,S2,…,Sn-1為中間待規劃的航跡點。
在無人機航跡規劃過程中需要考慮無人機機動能力、地形、威脅等約束,具體如下。
(1) 最大轉彎角約束:受無人機機動性能的約束,規劃的航跡需要避免過大的轉彎角,以保證航跡合理可行。假設最大轉彎角為θmax,則最大轉彎角約束可表示為
θi≤θmax
(1)
式中,θi表示第i航跡點處的轉彎角,i=1,2,…,n。
(2) 最大爬升/俯沖角約束:受無人機推力、重力等因素的影響,無人機的爬升/俯沖能力存在一定的極限值。假設無人機最大爬升/俯沖角為Φmax,則最大爬升/俯沖角約束表示為
Φi≤Φmax
(2)
式中,Φi表示第i航跡點處的爬升/俯沖角。
(3) 最小航段長度約束:受無人機機動性能限制,無人機每次改變航向前必須保證一個最短的直線飛行距離。假設無人機最短直飛距離為lmin,則最小航段長度約束表示為
li≥lmin
(3)
式中,li表示第i段航跡的長度,其表達式為
(4)
(4) 最小相對高度約束:為了保證無人機的飛行安全,飛行過程中無人機需與地面保持一定的相對安全距離。假設允許的最小相對高度為hmin,則最小相對高度約束可表示為
z-hT≥hmin
(5)
式中,hT表示無人機正下方的地形海拔高度。
(5) 禁飛區約束:假設環境中有M個威脅(文中考慮圓柱威脅),為保證飛行安全,要求無人機在任意時刻都位于威脅區域外部,即?m∈{1,2,…,M},有
‖s(t)-pm‖2≥rm,?t∈[t0,tf]
(6)
式中,pm=[xm,ym]T為第m個威脅的位置;rm為對應威脅的半徑。
2 AR-SAS航跡規劃算法
本節將即時修復式構架與SAS算法相結合,并引入雙排序準則、存儲空間約束及變步長策略,提出了AR-SAS動態航跡規劃算法。下面針對AR-SAS算法流程及其中應用的改進策略分別展開描述。
2.1 AR-SAS算法流程
AR-SAS算法通過將SAS算法[26]嵌入到即時修復式架構中,實現兩者優勢的結合,利用將航跡約束加入節點擴展過程的策略以縮小搜索空間、加快算法收斂速度和保證航跡結果可行性,同時基于即時修復式架構實現極短時間內可行航跡的生成以及后續對現有航跡的不斷優化。此外,通過引入雙排序準則、存儲空間約束以及變步長策略,克服了即時修復式構架中低啟發項偏好缺陷以及算法效率對規劃區域和障礙尺度敏感的問題,提升了算法的魯棒性。
AR-SAS算法偽代碼如表1所示,其中調用的定制加權SAS算法偽代碼如表2所示。
AR-SAS算法的詳細步驟如下:
步驟1(2-3行):節點鏈表初始化,并將目標點真實代價(即初始最優航跡的長度)設為無窮大;
步驟2(4行):判斷規劃是否超出時限或啟發項權重系數ε1是否小于1,若是則算法退出并輸出當前最優航跡,否則執行步驟3;
步驟3(5行):根據輸入的起終點、當前啟發項權重系數以及擴展步長使用定制加權SAS算法進行單次可行航跡規劃;
步驟4(6-7行):由CLOSED表節點回溯獲得當前規劃航跡并保存;
步驟5(8-12行):根據規則減小啟發項權重ε1、ε2和擴展步長;
步驟6(13-14行):將INCONS表中節點移入OPEN表中并根據新的啟發項權重更新節點代價,返回步驟2。

表1 AR-SAS算法偽代碼Table 1 Pseudo code of AR-SAS

表2 定制加權SAS算法偽代碼Table 2 Pseudo code of customized weighted SAS
針對AR-SAS算法架構定制的加權SAS算法詳細步驟如下:
步驟1(1行):判斷OPEN表中所有節點代價key(s,1)中最小值是否小于目標節點真實代價(即當前最優航跡的長度),若是則進行步驟2,否則退出;
步驟2(2-5行):判斷當前擴展節點是否滿足g(s) 步驟3(6-7行):將該節點移入CLOSED表作為當前擴展節點并擴展該節點; 步驟4(8-16行):根據各擴展子節點的信息將各個子節點放入對應的節點鏈表中; 步驟5(17-18行):判斷OPEN表節點數量是否超出存儲界限,若是刪除key(s,2)較大的節點直至滿足存儲界限約束,返回步驟1。 AR-SAS算法中代價函數計算、啟發項權重和鏈表更新、節點擴展及收斂條件判斷的具體方法分別如下所述。 (1) 代價函數計算 AR-SAS算法在節點擴展過程中代價函數的一般形式可表示為 f(s)=g(s)+ε×h(s) (7) 式中,g(s) 表示從起始點到當前節點s的真實代價;h(s) 表示當前節點到目標節點的估計代價;ε為啟發項權重系數(ε≥ 1)。 為了快速得到可行航跡,初始啟發項權重一般較大,導致算法不再具有可接納性[31]且不滿足一致性[32]條件。因此在迭代搜索路徑的過程中,AR-SAS同時保存3個節點鏈表,即OPEN表、CLOSED表和INCONS表。OPEN表保存未擴展節點,CLOSED表保存已擴展節點,INCONS表保存具有非一致性的節點。 當AR-SAS搜索重復擴展至CLOSED表中某一節點,并使該節點的g值下降時,則更新該節點代價值,并將該節點放入INCONS表中。INCONS表中的節點不會被立即擴展,而是會在下一次迭代搜索過程與OPEN表合并,并重新排序進行擴展。 (2) 啟發項權重和鏈表更新 在完成單次航跡規劃后,若規劃時間還沒超出限度,則進行啟發項權重和節點鏈表更新,并以此進行下一次的加權SAS規劃。 AR-SAS算法中啟發項權重的更新采用線性縮減方式,表示為 ε=ε-Δε (8) 式中,Δε參考文獻[22]的經驗值取為0.1。 鏈表的更新包括:將CLOSED表置空;將INCONS表中節點移入OPEN表,并將INCONS表置空;將OPEN表中的節點代價值按新的啟發項權重進行重新計算。 (3) 節點擴展 為了有效縮減節點搜索空間,縮短規劃時間,AR-SAS算法將最小航跡長度、最大轉彎角和最大爬升/下滑角等飛行器動力學約束以及飛行高度、禁飛區和地形限制等環境約束條件結合到節點擴展過程中,若節點不滿足飛行器動力學約束或與環境約束沖突,則該節點被視為無效節點,不再擴展。 (4) 收斂條件 標準SAS算法只執行單次搜索,其搜索退出條件為目標點被擴展,而在AR-SAS算法中,由于每次執行加權SAS算法時都會根據新的啟發項權重對OPEN表節點進行代價更新,因此每次執行加權SAS算法的退出條件為 f(sgoal) (9) 式中,sgoal表示目標節點;f(sgoal)表示當前路徑代價;mins∈OPEN(f(s))表示OPEN表中所有節點代價的最小值。單次加權SAS算法搜索過程中,若OPEN表中所有節點的代價值均大于當前路徑代價,則退出該次路徑搜索。 針對即時修復式構架中低啟發項偏好缺陷和算法效率對規劃區域和障礙尺度強烈敏感的問題,本節提出了雙排序準則、存儲空間約束及變步長策略,以進一步提升AR-SAS算法的魯棒性和搜索效率,具體描述如下。 (1) 雙排序準則 當AR-SAS算法完成一次搜索后,將INCONS表中節點移入OPEN表中,OPEN表將依據新的啟發項權重系數更新表中節點信息。由于啟發項權重的影響,距離目標節點sgoal附近的節點明顯具有更低的代價值,在算法對OPEN表排序時這些節點也將優先被擴展,而起始點附近的未擴展節點只有在啟發項權重較小時才會被考慮擴展。因此當最優航跡與當前找到的次優航跡在遠離目標點的位置發生分叉,則啟發項權重需要縮減至一個較小的值時算法才能找到當前存在的最優航跡,這一缺陷降低了AR-SAS算法收斂至最優航跡的速度。搜索過程中,前半部分的路徑選擇在很大程度上影響最終的結果,并且較低的啟發項權重意味著大量的節點擴展,導致搜索效率的下降。 為了解決這一問題,加快算法尋找最優解的速度,可以在搜索的不同階段采用不同的啟發項權重。因此,本文提出一種雙排序準則,在節點擴展過程中保存兩個代價信息,記為key(s,1)和key(s,2),其表達式為 (10) 式中,ε1、ε2為啟發項權重系數,并且ε1>ε2。 在航跡搜索的前半部分,即當前節點滿足g(s) (2) 存儲空間約束 為了搜索到當前存在的最優解,啟發項權重需要下降到一個較小的值,這會增加OPEN表內的節點數量,導致OPEN表中節點代價更新消耗大量的計算時間。實際上,許多待擴展節點無法導向一個更優的航跡結果,因此在搜索過程中可以刪除OPEN表中部分無用節點以提高航跡規劃的效率。 同時,對于節點代價f(s)=g(s)+ε×h(s),若其啟發項權重系數越小,則該代價越接近經過該節點的最優路徑的實際代價。因此為了避免錯誤刪除可能位于最優路徑上的節點,根據起終點歐式距離和擴展步長比例設置OPEN表節點存儲界限。當OPEN表中的節點數超出存儲界限,則刪除key(s,2)較大的節點,以保證OPEN表中的節點數目在約束范圍之內。例如將OPEN表節點數量限制為n,一旦航跡迭代搜索過程中節點擴展數量超過存儲限制n,則按照key(s,2)對節點代價進行排序,并移除其中代價值較大的節點,以滿足存儲空間約束,提升搜索效率。 (3) 變步長策略 為保證飛行安全,標準SAS的擴展步長必須大于最小航長約束lmin,具體數值根據實際需求設定。擴展步長取值過大會導致航跡質量較差,取值過小則影響求解效率,且容易陷入局部搜索。為了加快初始航跡規劃速度并保證算法退出時航跡的最優性,采用變步長的策略進行迭代規劃,即初始搜索時使用較大的擴展步長,在獲得初始航跡后,逐次減小擴展步長進行迭代搜索以獲得最優性更好的航跡。另外,SAS算法對OPEN表節點的代價計算與排序會消耗大量的計算時間,使用較大的擴展步長能有效減少OPEN表中的節點數目,提高初始規劃效率,并且避免算法在地形或威脅復雜區域的擴展陷入局部搜索。例如在特定環境下,綜合考慮威脅信息和無人機飛行性能,確定最大擴展步長lmax和最小擴展步長lmin,為提升可行航跡規劃速度,使用lmax作為初始擴展步長,并隨著航跡迭代過程的進行,線性減小擴展步長,以提升航跡規劃質量,當步長減小到lmin時則不再減小。 本節首先在三維靜態環境下分別使用分層SAS[12-13]、標準SAS[26]和AR-SAS 3種算法進行蒙特卡羅仿真試驗,從多個方面對比各算法的計算時效性和最優性。然后在三維動態環境下,使用AR-SAS算法進行動態航跡規劃仿真試驗,以驗證算法在動態環境和有限規劃時間條件下的航跡規劃能力。 三維靜態環境下將敵方威脅建模為半徑4~5 km不等的圓柱,任務規劃區域為60 km×60 km的方形區域,地形數據為某山脈高程地形,并假設飛行器最小轉彎半徑為1.5 km,最大飛行高度為1 000 m,最小離地高度為50 m。 算法設置方面,初始啟發項權重ε1=3、ε2=1.2,迭代縮減值Δε=0.1,初始擴展步長取為最大威脅半徑,即l0=5 000 m,迭代縮減步長Δl=500 m,最小擴展步長為無人機最小轉彎半徑,即lmin=1 500 m,OPEN表節點存儲容量300,規劃退出時間15 s。 為了對比AR-SAS算法同分層SAS和標準SAS兩種算法的規劃性能,在地圖中的左上角和右下角10 km2范圍內隨機設置100組規劃起始點和目標點,分別使用AR-SAS算法、分層SAS算法和標準SAS算法進行蒙特卡羅仿真試驗,并統計各算法的可行航跡、最優航跡規劃時間及航跡代價。由于規劃起點與終點隨機選擇,不同試驗中航跡絕對代價值變化非常大,為了便于比較,本文將規劃航跡長度除以起點到目標的歐式距離定義為航跡相對代價,并將其作為各算法最優性的評價指標。 靜態環境下,3種規劃算法的仿真結果對比如圖1所示。 圖1 三維靜態環境各算法航跡規劃結果對比Fig.1 Path planning results of different planning algorithms in 3D static environments 圖1(a)所示為AR-SAS算法生成的航跡結果。由圖1(b)可知,AR-SAS算法在可行航跡規劃的時效性上具有明顯的優勢,在1 s的時間內即可規劃出航跡;分層SAS算法的航跡平均求解時間為2.57 s;標準SAS算法的航跡平均求解時間為12.11 s,并且在100次仿真試驗中有5次未能在15 s內規劃出可行航跡。圖1(c)所示為最優航跡相對代價對比,AR-SAS算法規劃出的航跡代價與分層SAS算法接近,并優于標準SAS算法。圖1(d)為某一次仿真試驗中航跡代價隨規劃時間的變化曲線(在算法未規劃出可行航跡之前代價為無窮大),可以看出分層SAS和標準SAS算法均是通過一次規劃得到可行較優的航跡,并且標準SAS算法耗時相對較長;而AR-SAS算法在很短時間內即可規劃出可行航跡,并能夠繼續進行優化,在達到規劃時限時得到了與標準SAS和分層SAS算法最優性相當的可行航跡。 表3給出了100次試驗中3種算法得到初始可行航跡和最優航跡時OPEN表和CLOSED表中節點數量的平均值。由于分層SAS算法和標準SAS算法只進行單次航跡規劃,因此它們找到可行航跡和最優航跡時,節點鏈表中的節點數不變。 表3 不同算法的節點擴展數量對比Table 3 Comparison of expanding numbers of different algorithms 由表3可知,在完成可行航跡求解時,AR-SAS算法的OPEN表和CLOSED表的節點數量明顯小于其他兩種算法,大大縮減了規劃可行航跡時對OPEN表節點的排序和代價計算時間,提高了可行航跡的求解速度。 為了驗證AR-SAS算法在動態環境下即時航跡規劃的性能,在三維戰場環境中設置移動威脅和運動目標,并假設移動威脅與運動目標均以15 m/s的速度作勻速運動,其中目標運動方向隨機,移動威脅沿與x軸成夾角45°方向作直線折返移動。 戰場環境示意如圖2所示,圖2中藍色五角星為起點坐標(3 000 m,51 000 m),紅色星形為運動目標初始坐標(58 000 m,8 000 m)。 圖2 動態環境示意圖Fig.2 Diagram of dynamic environment 環境中的威脅信息如表4所示。 表4 威脅信息表Table 4 Information of threats 考慮到威脅和目標的連續機動過程,采用滾動規劃策略,每間隔10 s調用航跡規劃算法完成當前點到運動目標點的動態航跡重規劃。由于動態規劃的實時性要求,算法規劃時間限定為0.2 s,其余設置與第3.1節相同。 假設每次動態規劃前,無人機能夠通過偵察獲取移動威脅和運動目標的當前位置和速度。動態規劃過程中考慮當前威脅的移動速度和方向,并且在一個規劃周期內,移動威脅的速度方向和大小保持不變。因此動態規劃輸入的威脅位置可由式得到 (xinput,yinput)Threat=(xi,yi)Threat+VThreat×T (11) 式中,(xi,yi)Threat表示第i個威脅的當前位置;VThreat表示威脅移動速度;T為動態規劃周期。 仿真結果如圖3、圖4及表5所示。其中圖3和圖4分別為AR-SAS算法動態航跡規劃過程的三維和二維示意圖。白色三角形表示無人機當前位置,紅色五角星表示運動目標當前位置,紅色米形表示運動目標初始位置,紅色圓柱表示移動威脅當前位置,藍色圓柱表示移動威脅初始位置。 圖3 AR-SAS動態航跡規劃過程(3維)Fig.3 Process of AR-SAS dynamic path planning (3D) 圖4 AR-SAS動態航跡規劃過程(2維)Fig.4 Process of AR-SAS dynamic path planning (2D) 表5 動態環境下航跡規劃仿真結果Table 5 Simulation results of dynamic path planning 由表5可知,使用AR-SAS算法進行動態航跡規劃時,整個仿真飛行過程持續701 s,當無人機到達目標點5 km范圍(5 km為無人機偵察范圍,當目標進入無人機偵察范圍內則轉入自動導引階段)內不再進行規劃。仿真過程中共調用65次AR-SAS算法進行動態航跡規劃,并全部在規定時限內找到可行較優航跡,無人機飛抵運動目標的過程中成功規避所有威脅(如圖3~圖4所示)。上述數值仿真試驗結果表明本文提出的AR-SAS算法能夠滿足動態環境下的無人機航跡規劃需求,具有較高的規劃效率和較強的魯棒性。 根據靜態環境和動態環境下的仿真結果與分析可知,相較于傳統的SAS算法及分層SAS算法,本文提出的AR-SAS算法可以在很短的時間內規劃出可行航跡并充分利用規劃時間持續優化航跡,既能夠在靜態環境中以較高的效率搜索得到較優的可行航跡,也能適應動態環境下規劃時效性與最優性的嚴苛要求,具有較強的魯棒性。 提出了即時修復式構架與SAS算法相結合的AR-SAS算法,該算法能夠快速規劃出可行航跡,并隨規劃時間的增加不斷提高航跡質量。考慮航跡規劃擴展中的運動學約束并針對即時修復式構架中的缺陷,引入雙排序準則、存儲空間約束及變步長策略,在保證航跡最優性的同時,顯著提升了規劃效率和魯棒性。 仿真測試結果表明,AR-SAS算法的規劃效率高于分層SAS和標準SAS算法,能夠即時處理動態環境下的航跡規劃問題,具有較強的工程實用性。2.2 AR-SAS算法策略
3 仿真對比分析
3.1 三維靜態仿真試驗

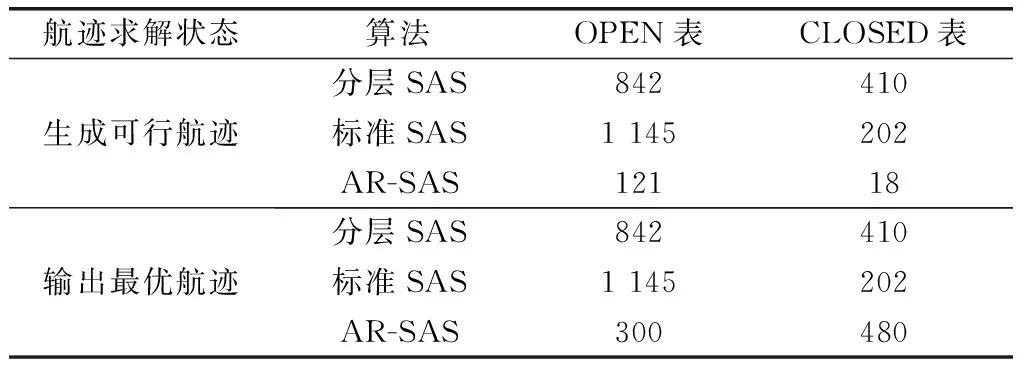
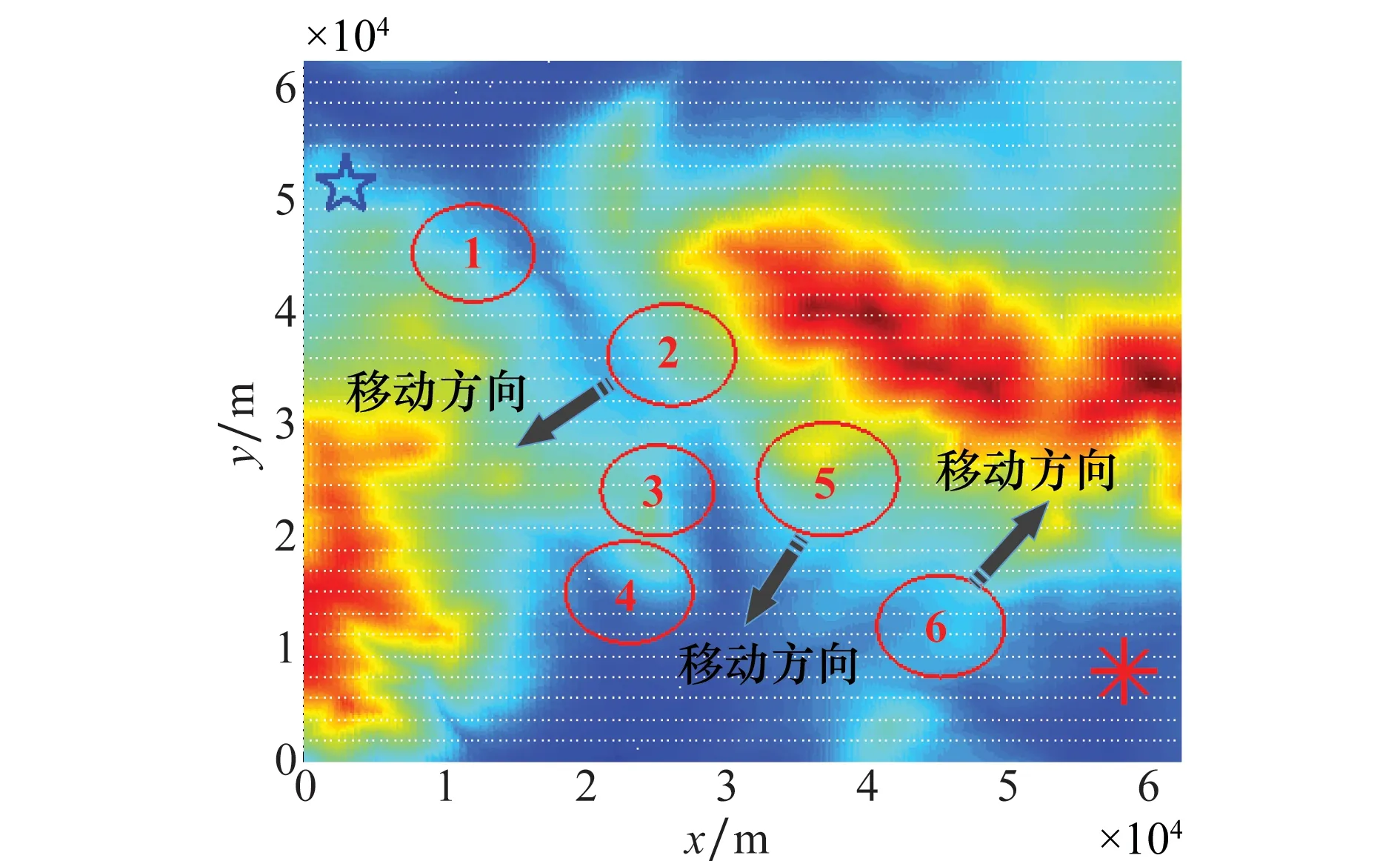
3.2 三維動態仿真試驗

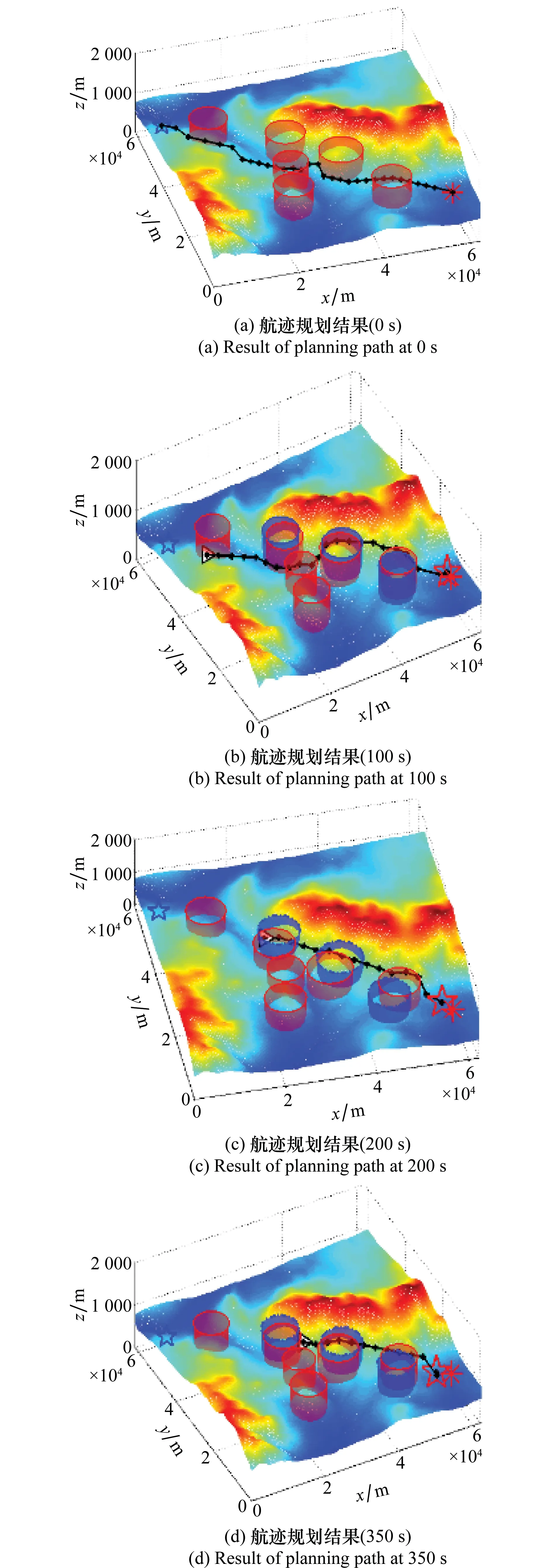


4 結 論

