城市道路交通基礎設施養護資金配置的優化

趙悅彤 何永泰 周愷 王路

摘? ?要：本文調查評價某城區城市道路交通基礎設施服役和養護維修狀況，基于AHP層次分析法對設施進行優先級排序，并針對城市路網交通基礎設施養護決策中多選擇多維背包問題，采用DEA數據包絡分析法研究網級養護資金分配優化的項目規劃問題。

關鍵詞：交通基礎設施;養護資金分配優化;AHP層次分析法;DEA數據包絡分析法

中圖分類號：U418? ? ? ? 文獻標志碼：A

0 引言

交通基礎設施是城市發展的基礎，在荷載與環境等因素作用下性能衰減，為維持性能，許多學者進行了深入研究，有代表性的方法有：按使用性能參數和經濟分析參數排序的排序方法;線性和非線性規劃法、動態規劃法等方法。然而仍存在不足：以城市道路為研究對象較少;缺乏對相關附屬設施的協同考慮;基礎設施養護成本及資源分配優化多為單一目標。因此，基于多目標的交通基礎設施養護資金優化就尤為必要。

本文選取某城區典型11條城市道路，基于多目標對交通基礎設施養護決策進行優化。養護資金不足以覆蓋各交通設施時，采用AHP層次分析法確定養護順序;資金足以覆蓋各設施時，通過DEA數據包絡分析優化資金分配，提高養護效果。

1 某城區部分典型路段交通基礎設施調查與評價

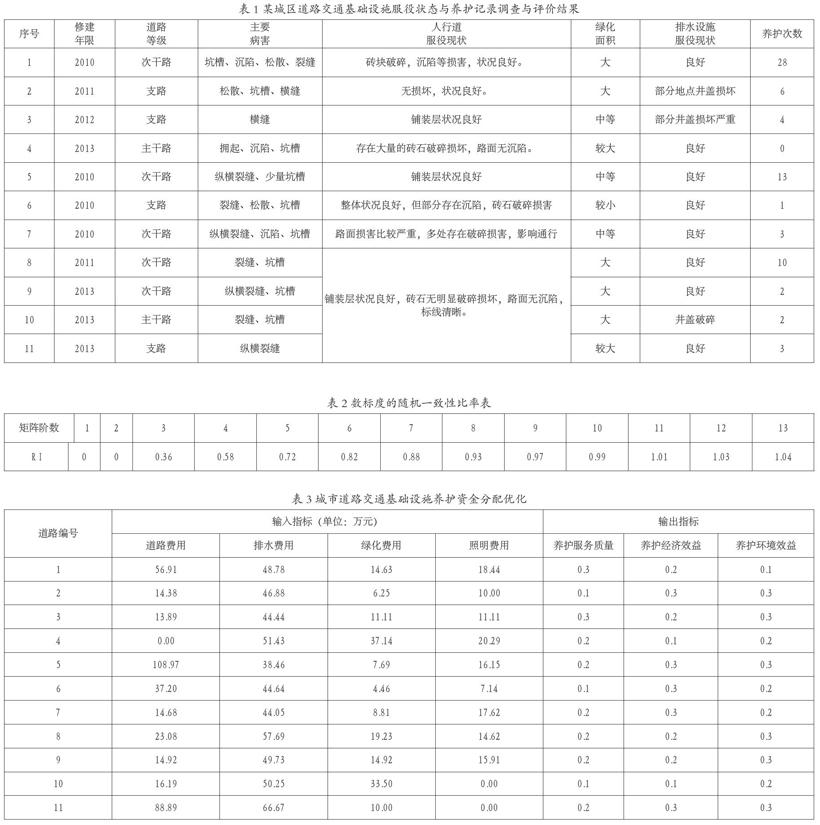
調查表明，某城區部分道路（路面結構：7cmAC-20瀝青砼+5cmAC-13瀝青砼）交通基礎設施服役狀態普遍良好，壽命期內無大中修記錄。調查與評價結果見表1。

2 基于AHP層次分析法的養護設施優先級排序

構建交通基礎設施的判斷矩陣，將道路、排水、人行道、綠化、照明設施按照指數標準進行兩兩比較，比較結果寫成正互反矩陣的形式，各設施重要性等級矩陣如式（1）所示。

（1）

各行求和得到各設施的得分矩陣：B=[8.86? 6.18? 5.34? 4.30? 3.72]T，根據得分矩陣中各元素占比即可求出功能重要性系數矩陣（權重向量）如式（2）所示。

C=[0.311? 0.218? 0.188? 0.151? 0.131]T? ? ? ? ? （2）

在此基礎上，對得到的功能重要性矩陣進行一致性檢驗。

（3）

ci—權重向量中的第i個元素;λ—最大特征根的近似值，取λmax=4.760。

一致性指標：

（4）

隨機一致性比率：

（5）

RI——隨機一致性比率，按照表2取值。

由于|CR|<0.1，根據上述計算過程可以得出矩陣A通過一致性檢驗的結論，特征向量C=[0.311? 0.218? 0.188? 0.151? 0.131]T就是所求的權重。考慮到排水設施作為城市道路排水的主要途徑，直接關系到洪澇季節排水安全，故而微調整后的養護優先級順序為路面、排水、人行道、綠化、照明設施。

3 基于多目標的養護資金分配優化

本部分網級決策優化依托調查的某城區部分道路組成的道路網，采用DEA數據包絡分析在資金足以覆蓋各設施的情況下進行分配優化，當養護資金不足以覆蓋各設施時參考AHP層次分析法得出的養護順序優先級。

3.1 DEA算法輸入輸出指標的選取

本文選取單位里程年平均養護費用為輸入指標，選取路網整體養護服務質量、養護經濟效益、養護環境效益為輸出指標，并采用專家打分法進行打分。輸入輸出指標見表3。

3.2 模型求解

C2GS2模型求解，對求解結果分析：S1-=S2-=S3-=S4-=S1+=S2+=S3+=0，共有道路2、道路3、道路5、道路6、道路7、道路10和道路11共7條道路，也就是這7條道路的DEA有效，其分配于道路、排水、照明和綠化設施的養護資金最佳，養護效果最優，資金不需要再做調整。而道路1 S1-=19.7250，S3+=0.0647;道路4 S1-=42.1066，S3-=21.4708，S3+=0.0533;道路8S4-=7.4800;道路9S1-=6.3679，S3-=2.5897，可知這4條道路資金比例分配嚴重不合理，利用率低，應該建議相關部門進行調整。

按照上述模型求解結果對某城區的11條城市道路養護資金進行最優分配求解，通過DEA優化，可以對養護資金進行合理的資金比例分配優化，使資金得到了更高價值的使用，最終養護效果提升。因此DEA優化方法在城市道路養護資金分配中具有很明顯的提升效果。

結語

（1）對某城區11條城市道路交通基礎設施的服役狀態及養護現狀進行了實地調查分析，該城區道路病害主要表現為裂縫、坑槽、松散和沉陷。

（2）運用AHP層次分析法確定在養護資金不足以覆蓋各交通設施條件下的養護優先級順序為：路面、排水設施、人行道設施、綠化設施、照明設施。

（3）選取某城區11條典型道路，基于養護資金分配歷史，以尋求路網整體養護效益最大為目標進行DEA決策優化，經分析發現道路1、道路4、道路8和道路9資金比例分配嚴重不合理，建議相關部門進行調整。

參考文獻

[1]Shahin M Y，Kohn S D.OVERVIEW OF PAVER PAVEMENT MANAGEMENT SYSTEM[M].1982.

[2]Hadley W O.SHRP-LTPP OVERVIEW：FIVE-YEAR REPORT[J].Continuously Reinforced Concrete Pavements，1994.

[3]李玲娟，豆坤.層次分析法中判斷矩陣的一致性研究[J].計算機技術與發展，2009，19（10）：131-133.