糧食作物巨災保險的純費率厘定

梁來存，皮友靜

（廣西財經學院a.信息與統計學院；b.圖書館，南寧 530003）

0 引言

為積極開展糧食作物的巨災保險業務，使政府的保費補貼額度與各地區的風險水平、費率水平相適應，有必要厘定出各地區糧食作物的巨災保險費率，為我國政策性糧食作物巨災保險的健康發展提供技術支持。以往研究探討的是農作物保險費率的厘定方法，并未涉及農作物巨災保險的費率厘定問題。糧食作物巨災事件屬于極值事件，可以基于極值理論進行研究。根據PBDH定理，災損數據極端值的分布可以選擇廣義帕累托分布（GPD）。即，糧食作物巨災保險的費率厘定可參照參數法思路，以GPD作為災損數據的尾部分布，基于極值理論界定巨災，估計并檢驗GPD參數，進而厘定糧食作物巨災保險的純費率。

1 研究方法

1.1 災損數據的推算

設農民以糧食作物的單產投保。i地區第t年的實際單產為yit，根據趨勢方程可求得趨勢單產為it。可以這樣獲取災損數據：將實際單產yit與趨勢單產it比較，如果yit≥it，則認為i地區第t年的糧食作物生產沒有遭受自然災害，該地區該年的災損數據為0；反之，如果yit＜it，則認為i地區第t年的糧食作物遭受了自然災害，該地區該年的災損數據為it-yit。所以，i地區第t年的災損數據xit為：

1.2 巨災界定值的初步估計

1.2.1 巨災界定的理論依據

Balkema&Dehann（1974）,Pickands（1975）證明了超額災損數據的分布函數在MDA條件下收斂于GPD。 即 當μ→x0時-μ}→0。這就是PBDH定理。該定理的統計意義在于，可以用GPD來擬合高出門限值的那一部分數據。

可見，只有估計了門限值μ，才能依據前述的災損數據和門限值μ，確定巨災年份，并得到超額災損數據z。依據PBDH定理，超額災損數據z趨于GPD，據此計算z的期望值E(z)，則E(z)+μ為巨災數據的期望值。所以，要計算巨災年份巨災數據的期望值，要厘定巨災保險的費率，估計門限值μ是必要的。

1.2.2 巨災界定值的初步估計法

如果某地某年糧食作物的單產災損超過了門限值μ，則認為糧食作物遭受了巨災；如果單產災損在μ或μ以下時，則認為沒有遭受巨災。初步估計門限值μ的方法，一是樣本平均超出函數法，根據en(μ)關于μ的分布圖來選擇確定一個適當的門限值：如果en(μ)在超過某一門限值μ后呈現明顯的正斜率的線性變化，說明數據服從GPD；如果en(μ)在超過某一門限值μ后呈現明顯的負斜率的線性變化，說明數據呈薄尾分布；如果呈一條水平線，則是指數分布。二是正態近似法。McNeil和Frey提出，當假定災損數據隨機變量x的分布函數左邊和中間都是正態分布、右尾是GPD時，根據F(x)的右連續性可知，可以取滿足的最大的x作為門限值。這里Φ(x)是具有和歷史數據相同均值和方差的正態分布的分布函數，n是樣本容量，Nu為大于門限值μ的數據的個數。三是峰度法。該方法是由Pieere Patie（2000）提出來的，其依據是，正態分布的峰度系數等于3，厚尾分布的峰度系數大于3。因此，可以這樣來估計門限值：每次將災損數據中使得| |xi-xˉ值最大的xi從數據中刪除，一直到刪除后的剩余數據的峰度系數近似地等于3。此時，這些剩余數據組成的樣本呈正態分布，該樣本中的最大值即可作為巨災的門限值。

1.3 巨災界定值的確定

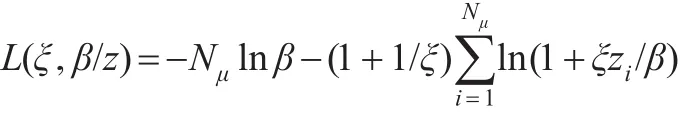
當ξ≠0時 ，對L(ξ，β/z)求極值，令偏導數等于0，可以解得使函數值L(ξ，β/z)最大的參數（ξ、β）的最佳估計量ξ是分布的形狀參數，β是分布的尺度參數。

建立的GPD模型還需要進行檢驗。根據V.Choulakian和M.S.Stephens（2001）的研究，檢驗GPD模型可使用假設檢驗法。原假設H0：樣本來自于GPD。并計算統計量：

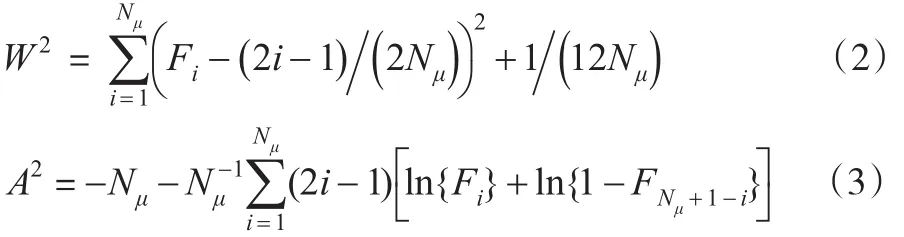
在上一步中，已經得到了巨災界定值的初步估計值。對該值及其附近可能的門限值，逐一進行上述檢驗，直到檢驗通過為止，這時的巨災界定估計值即為最終確定的巨災界定值。

1.4 計算純費率

當農民以單產投保時，設保障程度為λ，投保年份的趨勢單產為it。由于糧食作物保險的純費率為糧食作物的平均損失率，那么，糧食作物巨災保險的純費率等于所有年份巨災損失的期望值與保障水平之比。而所有年份巨災損失的期望值可以通過巨災年份巨災損失的期望值與巨災發生的概率之積來計算。因此，糧食作物巨災保險的純費率為：

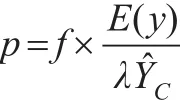
其中，y-μ=x，x為單產巨災損失超出額。根據PBDH定理，x服從GPD分布，因此有：

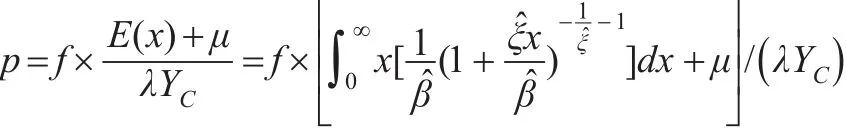
式中，f為巨災發生的頻率，、分別為GPD分布的形狀參數、尺寸參數的估計值。

2 實證

假定農民以單產投保，單產的變化幅度反映了所有自然風險對稻谷作物的影響程度，這里以我國稻谷為例，厘定我國稻谷作物巨災保險的純費率。

2.1 數據搜集與災損數據推算

2.1.1 數據搜集

根據相關年份的《中國農村統計年鑒》，可以搜集到我國各省（市、區）稻谷作物1979—2015年分省、分年的實際單產數據yit（公斤/公頃）。由于青海省的相關數據不全，且不含港澳臺地區，所以，這里只包含30個省（市、區）。

以省（市、區）為單位，為了得到各省（市、區）各年的單產趨勢值，采用趨勢方程擬合法。取1979—2015年各年的t為1～37（其中，廣東、海南只有1988—2015年的單產數據，故t取1～28；四川、重慶只有1997—2015年的單產數據，故t取1～19），根據各省（市、區）的實際單產數據，對各省（市、區）所擬合的單產趨勢方程見表1。

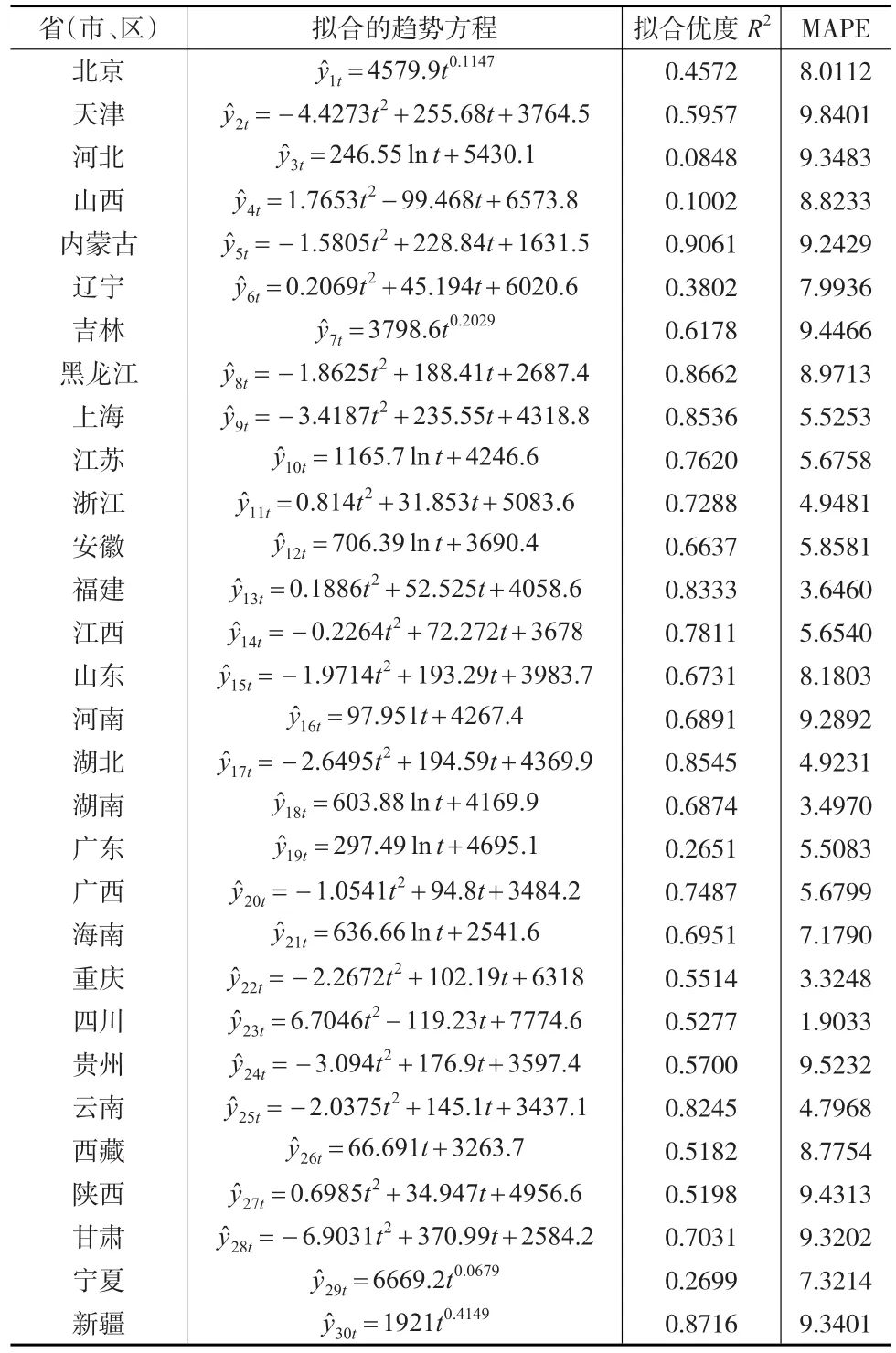
表1 各省（市、區）的單產趨勢方程表

從表1看，擬合精度指標MAPE值都小于10，符合精度要求，可以接受上述所建立的趨勢方程。

2.1.3 災損數據的推算。

將各年的對應t值代入表1的趨勢方程中，即可得到各省（市、區）各年的趨勢單產值。把各省（市、區）每年的實際單產與相應的趨勢單產代入式（1），便得到災損數據。對于這些災損數據，如果分省份分析，樣本容量為37，廣東、海南的樣本容量只有28，四川、重慶還只有19，樣本太小，無法對災損數據的分布形式進行較準確的判斷。

假定農民以單產投保，在巨災的影響下，單產的變化在各省（市、區）之間仍然具有可比性。以高單產地區為例，與低單產地區相比，一方面，由于單產相對較高，在同樣災害的影響下，單產的下降幅度會比較大；但另一方面，高單產地區的基礎設施往往相對完善，抵御自然災害的能力相對較強，單產的下降幅度會比較小。綜合這兩個方面，可以認為各地區間的單產變化具有可比性。因此，把各省（市、區）的災損數據作為一個整體進行分析，這是合理的。

2.2 巨災界定值的估計與確定

對于災損數據，是否存在巨災的界定值，還需要進行診斷，也就是厚尾性診斷。現對上述災損數據進行初步分析，分析結果表2所示。

表2 我國稻谷災損數據的統計分析指標

表2表明，災損數據總共有443個，最小值為0.58公斤/公頃，即平均畝產減少了0.58公斤/公頃，顯然這不是巨災。最大值為4010.02公斤/公頃，即平均畝產減少了4010.02公斤/公頃，無疑這屬于遭受巨災導致的減產。

峰度系數為9.95，遠遠大于正態分布的峰度系數3，不能用常用的正態分布作為災損數據的分布形式。偏度系數為2.25＞0，呈右偏分布。這就是說，我國稻谷的災損數據序列有極端值存在，即序列存在巨災數據。

對于上述的災損數據，樣本平均超出函數法、正態近似法都很難精確估計門限值。采用峰度法，利用MATLAB R2017a軟件，可以得到門限值為793.91公斤/公頃，大于該門限值的災損數據有91個。除去這91個巨災數據，余留下來的災損數據的峰度系數為2.99，相當于正態分布的峰度系數3。據此，可以估計，我國稻谷巨災的界定值，即門限值，在793.91公斤/公頃附近，巨災數據大概91個左右。

再利用V.Choulakian和M.S.Stephens（2001）提出的假設檢驗法來確定最終的門限值。對于初選的門限值793.91公斤/公頃及其附近的可能的門限值，采用極大似然法ML得到GPD的參數估計值和。利用式（2）計算W2,利用式（3）計算出A2。結果見表3所示。

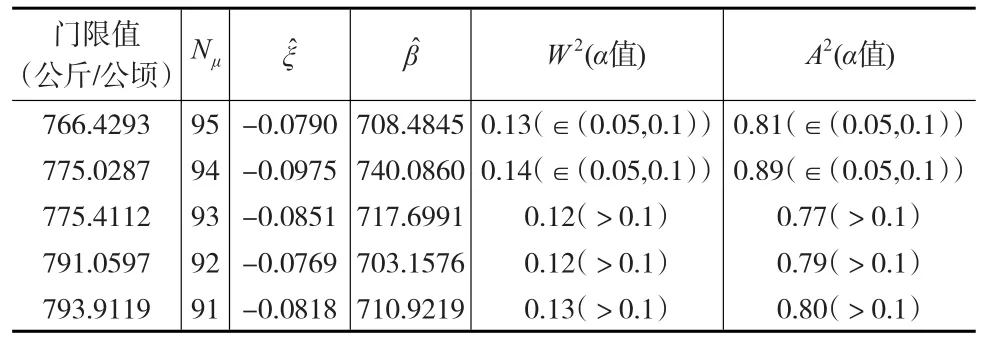
表3 門限值及其參數估計與檢驗表

在表3中，α值就是假設檢驗中的P值，當α值很小時，就有理由拒絕原假設H0。當門限值μ=766.42公斤/公頃，或者μ=775.02公斤/公頃時，在10%的顯著性水平上拒絕原假設H0，即相應的超額災損數據不服從GPD。當μ≥775.41公斤/公頃時，在10%的顯著性水平上接受原假設H0，即相應的超額災損數據服從GPD。為了盡可能擴大服從GPD的樣本的容量，則確定門限值μ=775.4112公斤/公頃，這就是稻谷單產巨災的界定值。超過該單產巨災界定值的災損數據，均為巨災數據。

從表3可以看出，門限值μ=775.4112公斤/公頃時，以最大似然法估計巨災損失的超出損失z的GPD的分布參數=-0.0851，=717.6991。據此可進一步厘定巨災保險的費率。

2.3 巨災保險的純費率厘定

根據上述估計得到的超出損失的GPD分布參數，計算單產巨災損失超出額的數學期望E(x)=661.4129。由于E(y)=E(x)+μ，則單產巨災損失的數學期望E(y)=661.4129+775.4112=1436.8241。

各地風險水平不一，要計算各省（市、區）的單產巨災損失的數學期望，還需要對E(y)進行調整，調整的依據為各省（市、區）的風險水平（表4）及政策取向。

表4 各省(市、區)糧食作物自然災害影響的分區結果

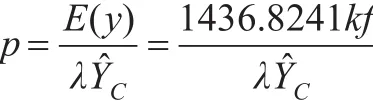
以風險系數k進行調整，各省（市、區）風險系數值與該地區的風險等級、政府的政策取向等因素有關,這里假設低風險區的風險系數為1.0，較高風險區為1.2，高風險區為1.4，如下頁表5第（1）列。巨災發生的頻率用f表示。各省（市、區）糧食巨災保險的純費率為：

3 討論

3.1 我國稻谷發生巨災的概率較高，巨災保險純費率較低

上述的實證研究選取了1979—2015年中國內地青海省以外的30個省（市、區）37年的數據。其中，廣東、海南只有1988—2015年28年的數據，四川、重慶只有1997—2015年19年的數據。這樣，樣本容量為1056。根據計算的巨災界定值，巨災數據共有93個。這樣，各省(市、區)平均發生巨災的概率達到8.81%。在巨災保險的純費率方面，計算各省（市、區）純費率的簡單算術平均數可知，如果保障程度為90%，純費率的平均值為2.33%；如果保障程度為100%，純費率的平均值為2.09%。

3.2 糧食主產區的巨災保險純費率偏高

我國有13個糧食主產區，保障程度90%時計算它們巨災保險純費率的平均值為2.17%。相應地，保障程度90%時全國的平均水平為2.33%。兩者相比，糧食主產區的純費率略低且相當接近全國平均水平。這說明，國家支持糧食主產區發展的相關政策，已經產生了積極的效果，基礎設施建設得到了加強，增強了抵御自然災害的能力。但是，主產區的糧食產量占全國糧食總產量的比重達到了70%左右，與主產區糧食生產的重要地位相比，其抵御自然災害能力仍然有待加強。

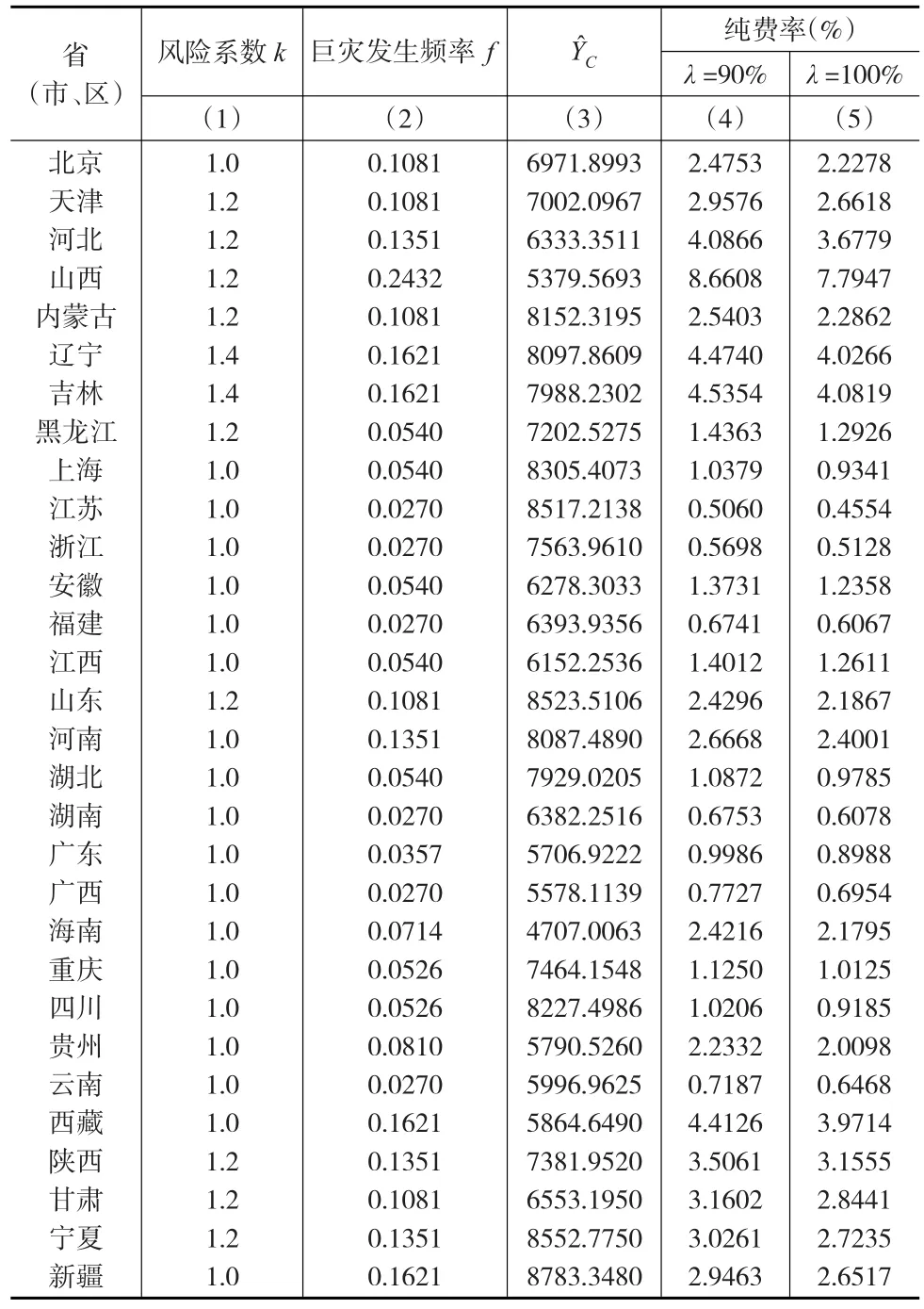
表5 各省（市、區）糧食巨災保險的純費率

3.3 稻谷巨災保險的純費率在全國呈北方高、南方低的區域分布特征

現以長江流域作為分界線，當保障程度為90%時，北方各省（市、區）巨災保險純費率的平均值為3.27%，而南方平均值為1.09%。如果將全國各省（市、區）的純費率按從大到小作降序排列，排前十位分別是：山西（8.66%）、吉林（4.53%）、遼寧（4.47%）、西藏（4.41%）、河北（4.08%）、陜西（3.50%）、甘肅（3.16%）、寧夏（3.02%）、天津（2.95%）、新疆（2.94%）。可見，這些純費率較高的前十位省（市、區），無一例外全部位于長江流域以北的地區。究其原因，一方面，反映北方地區糧食生產基礎設施建設的相對落后；另一方面，北方地區水資源的嚴重不足，已經成為制約其糧食生產的重要因素。

3.4 中、西部地區的純費率明顯高于東部地區

當保障程度為90%時，計算中、西部地區巨災保險純費率的簡單算術平均數為2.48%,而東部地區只有1.81%。根據上述全國各省（市、區）的純費率按從大到小作降序排列的情況看，排前十位的除遼寧、河北、天津外，其他七個都屬于中、西部地區。這主要因為東部地區經濟較發達，農業基礎設施建設相對健全、完善，抵御自然災害的能力相對較強，單產相對穩定，所以巨災保險的純費率較低。如果是同等程度的自然災害，對東部地區的糧食作物不會形成巨災，但對于中、西部地區來說，由于基礎設施建設不完善，則可能形成糧食作物的巨災。另外，東部地區水資源的相對充足也是原因之一。

4 結論

費率厘定主要有參數法和非參數法。本文按照參數法思路，即基于極值理論以GPD作為糧食災損數據的尾部分布，以門限值作為糧食作物巨災的界定值，采用費率即平均損失率的方法，探討了糧食作物巨災保險的費率厘定方法。并以稻谷為例進行了實證研究。結果表明，我國稻谷發生巨災的概率較大，達到8.81%，保障程度為90%時，巨災保險純費率的平均值為2.33%；保障程度為100%，平均值為2.09%；糧食主產區的平均純費率稍微低于全國平均水平，相對其糧食生產的重要地位來說顯得偏高；在區域分布方面，北方的平均水平明顯高于南方，中西部地區明顯高于東部地區。