條件矩約束下一階自回歸模型的參數(shù)經(jīng)驗(yàn)似然推斷

彭毳鑫，胡 敏，趙志文

（吉林師范大學(xué)a.大學(xué)外語部；b.數(shù)學(xué)學(xué)院，吉林 四平 136000）

0 引言

考慮如下的一階自回歸模型：

對(duì)于自回歸模型的統(tǒng)計(jì)推斷，一直是統(tǒng)計(jì)學(xué)家關(guān)心的熱點(diǎn)問題之一。常學(xué)將和劉維奇[1]討論了自回歸模型的模型識(shí)別及其參數(shù)的高階Yule-Walker估計(jì)；倪均援[2]討論了有AR殘差的自回歸模型的參數(shù)估計(jì)和定階問題；國(guó)春光等[3]提出一種求解擾動(dòng)項(xiàng)序列自相關(guān)系數(shù)及估計(jì)自回歸模型參數(shù)的迭代方法；林正華和馮仁忠[4]基于約束規(guī)劃及計(jì)算數(shù)學(xué)理論，給出了自回歸模型參數(shù)精確最小二乘估計(jì)方法；姜禮平[5]討論了有噪聲情形下自回歸模型參數(shù)的估計(jì)問題以及模型定階問題；呂效國(guó)等[6]研究了基于時(shí)間序列觀測(cè)數(shù)據(jù)，如何選擇自回歸模型的必要條件；吳鑑洪和朱力行[7]給出了一些診斷檢驗(yàn)工具，用于向量自回歸模型的擬合優(yōu)度檢驗(yàn)問題；Chen等[8]利用非參數(shù)方法——經(jīng)驗(yàn)似然方法估計(jì)自回歸模型參數(shù)。本文進(jìn)一步利用經(jīng)驗(yàn)似然方法，討論由輔助信息條件下模型（1）的參數(shù)估計(jì)問題。

經(jīng)驗(yàn)似然方法是Owen[9，10]提出的一種非參數(shù)估計(jì)方法。經(jīng)驗(yàn)似然方法有很多優(yōu)點(diǎn)，如置信區(qū)域由數(shù)據(jù)本身決定，經(jīng)驗(yàn)似然比統(tǒng)計(jì)量的極限分布為卡方分布，因此在構(gòu)造未知參數(shù)的置信區(qū)域時(shí)無需進(jìn)一步估計(jì)漸近方差等。經(jīng)驗(yàn)似然方法最初主要用于總體均值的參數(shù)估計(jì)。近些年，該方法也被用于時(shí)間序列模型的統(tǒng)計(jì)推斷問題，如Chan和Ling[11]討論了GARCH模型的經(jīng)驗(yàn)似然統(tǒng)計(jì)推斷問題；Chen和Gao[12]討論了時(shí)間序列回歸模型的適應(yīng)經(jīng)驗(yàn)似然檢驗(yàn)問題；Zhao和Wang[13，14]分別討論了具有解釋變量的自回歸模型和隨機(jī)系數(shù)自回歸模型參數(shù)的經(jīng)驗(yàn)似然統(tǒng)計(jì)推斷問題，構(gòu)造了未知參數(shù)的經(jīng)驗(yàn)似然比統(tǒng)計(jì)量，同時(shí)證明了統(tǒng)計(jì)量的極限分布為卡方分布；Chen等[15]討論了門限自回歸模型的經(jīng)驗(yàn)似然統(tǒng)計(jì)推斷問題。

在實(shí)際中，基于樣本觀測(cè)數(shù)據(jù) X0，X1，…，Xn，經(jīng)常能夠獲得一些輔助信息，這些輔助信息的形式多種多樣，如總體的分布為對(duì)稱的或非負(fù)的，方差是均值的函數(shù)等等。如果在統(tǒng)計(jì)推斷中有效的利用這些輔助信息，能夠提高統(tǒng)計(jì)推斷的精確性。本文中假定輔助信息能夠表示成為如下的條件矩：

其中 t=1，2，…，β0∈Rd為未知參數(shù)，g(Xt，Xt-1;β0)∈Rr，且 r≥d 。 為了敘述方便，將 g(Xt，Xt-1;β0)簡(jiǎn)記為 gt(β0)。條件矩約束（2）包含廣泛的輔助信息類，如果條件方差為某一已知常數(shù)，序列的二階條件矩等于某一常數(shù)等。本文利用經(jīng)驗(yàn)似然方法，給出模型（1）已知輔助信息（2）時(shí)，參數(shù)α的估計(jì)問題。

1 方法和主要結(jié)果

本文討論如何應(yīng)用經(jīng)驗(yàn)似然方法估計(jì)模型（1）中的未知參數(shù)α。假定如下條件成立：

A1:|α|＜1，即模型為平穩(wěn)遍歷的；

A2: 存在 β0使得 E(gt(β0))=0;

下面討論未知參數(shù)α的估計(jì)。

首先基于經(jīng)驗(yàn)似然方法，獲得數(shù)據(jù)驅(qū)動(dòng)的權(quán)。具體地，基于輔助信息 E(gt(β0))=0，令：

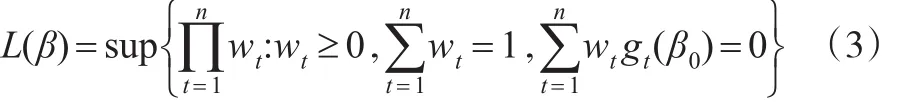
其中參數(shù)β0為待估的未知參數(shù)。由此可以獲得使L(β)達(dá)到最大的權(quán)w1，w2，…wn。基于該權(quán)函數(shù)，用如下的加權(quán)最小二乘方法估計(jì)未知參數(shù)α，即：

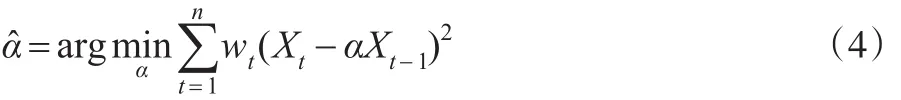
利用類似Owen[9]的方法，引入拉格朗日乘子λβ0∈Rr，經(jīng)過簡(jiǎn)單的代數(shù)運(yùn)算可知：

其中λβ0滿足：

利用權(quán)（5），可以得到α的估計(jì)：

下面的定理給出了的極限分布。

定理1：假定條件A1-A2成立。如果α0是未知參數(shù)α的真值，那么：

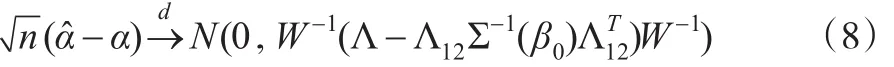
對(duì)于普通的最小二乘估計(jì)，其漸近方差為W-1ΛW-1。注意到Λ和Σ-1(β0)是正定的矩陣，因此與普通的最小二乘估計(jì)相比，本文所得到的估計(jì)的漸近方差減小。此結(jié)果進(jìn)一步說明由于引入輔助信息，從而提高了估計(jì)的效。對(duì)于估計(jì)表達(dá)式（7），由于參數(shù)β0未知，因此，在實(shí)際中還無法使用該表達(dá)式估計(jì)未知參數(shù)α。為此，進(jìn)一步使用最大經(jīng)驗(yàn)似然估計(jì)方法估計(jì)未知參數(shù)β0。具體地，令，利用Qin 和Lawless[16]的方法，進(jìn)一步可知：

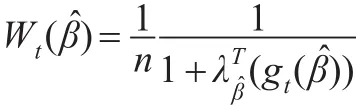
其中 (λβ，)滿足：

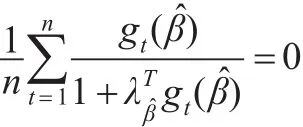
以及

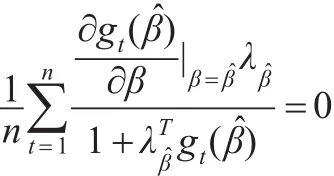
進(jìn)一步令：

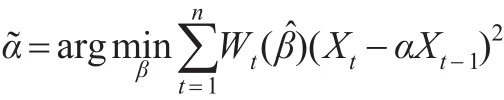
由此，可以用估計(jì)未知參數(shù)α。若r=d，即gt(β)的維數(shù)與β的維數(shù)相等，則，因此為普通的最小二乘估計(jì)。若r＞d，則加權(quán)最小二乘估計(jì)具有更小的漸近方差，因而與普通的最小二乘估計(jì)相比，加權(quán)最小二乘估計(jì)提高了估計(jì)的效。

下面的定理給出了估計(jì)量的極限性質(zhì)。

定理2：若條件A1-A2成立，EX4t＜+∞，如果α0是未知參數(shù)α的真值，那么：

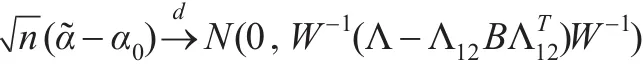
2 隨機(jī)模擬

下面通過隨機(jī)模擬來說明本文的方法的可行性。考慮如下的模型：

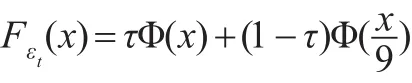
其中τ是固定的常數(shù)滿足0，＜τ＜1，Φ(x)是標(biāo)準(zhǔn)正態(tài)分布N(0，1)的分布函數(shù)。

計(jì)算具有輔助信息下加權(quán)條件最小二乘估計(jì)的均方誤差，即1000次估計(jì)誤差平方的平均值。樣本容量n=30， 50， 100。對(duì)于模型A，參數(shù)α分別取為-0.1，-0.2，-0.3，-0.4，-0.5，-0.6，-0.7，-0.8，-0.9，0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9，模擬結(jié)果由表1給出。對(duì)于模型B，參 數(shù)α分 別取為-0.1，-0.3，-0.5，-0.7，-0.9，0.1，0.3，0.5，0.7，0.9。τ分別取為0.8以及0.9表示不同的污染水平，模擬結(jié)果由表2給出。

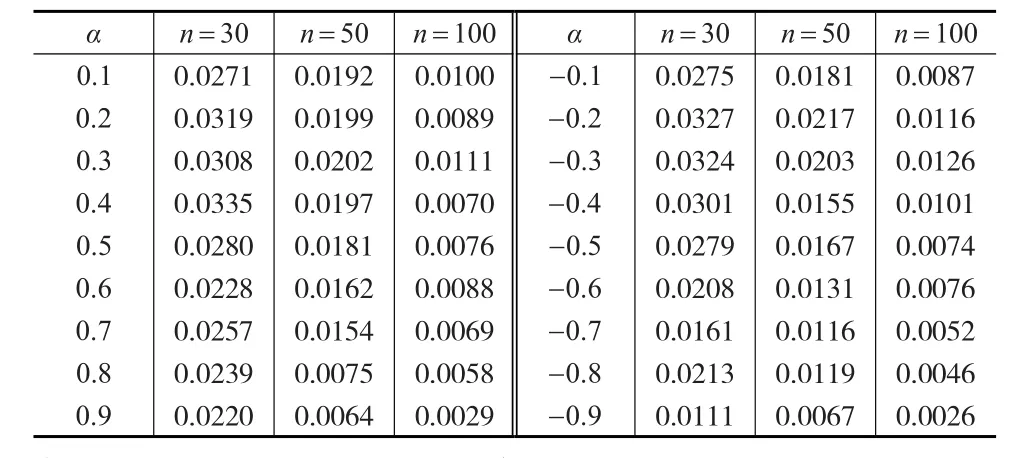
表1 模型A下參數(shù)估計(jì)的均方誤差

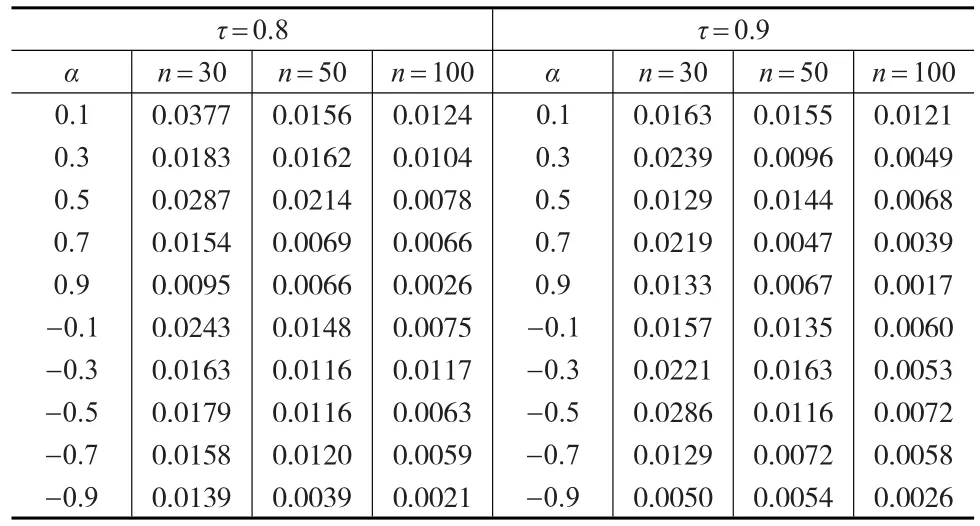
表2 模型B下參數(shù)估計(jì)的均方誤差

從表1和表2的模擬結(jié)果可以看出，對(duì)于不同的參數(shù)以及不同的樣本容量，本文的方法都具有較小的均方誤差，這也說明方法具有穩(wěn)健性。

3 定理的證明

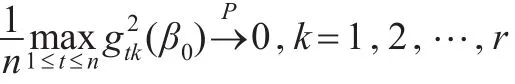
由條件A1可知：

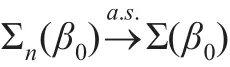
因此利用類似Peng等[17]引理1的方法證明，可以證明引理1成立。

引理2：假定A1-A2成立，EX41＜+∞，那么：

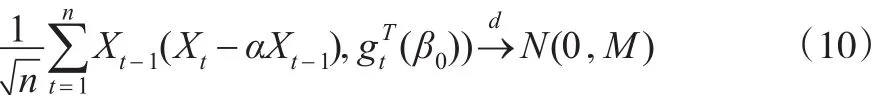
證明：由Cramer-Wold法則，只需證明對(duì)任意的非零向量C∈Rr+1，

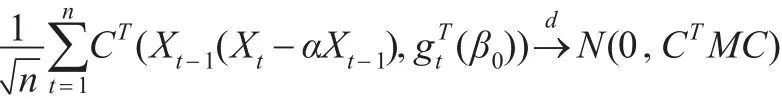
首先證明定理1，為此需要證明以下幾個(gè)引理。

引理1：假定條件A1-A2成立，那么：，因此：

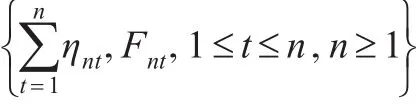
是零均值平方可積鞅陣，利用鞅的中心極限定理[18]只需證明：

以及

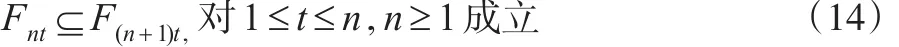
由σ代數(shù)的定義可知式（14）顯然成立。下面證明式（11），注意到對(duì)?ε＞0，

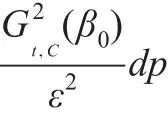
下面證明式（12）。由Lebesgue控制收斂定理可知：

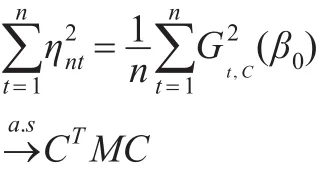
因此式（12）成立。

下面，證明（13）式。注意到：

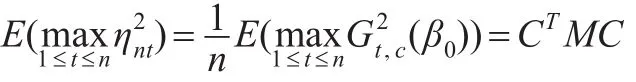
因此式（13）成立。綜上可知引理2成立。

引理3：假定A1-A2成立，EX41＜+∞，那么：

使用類似Owen[9]中的證明方法可以證明式（15）成立。

定理1的證明

由式（6）可知：

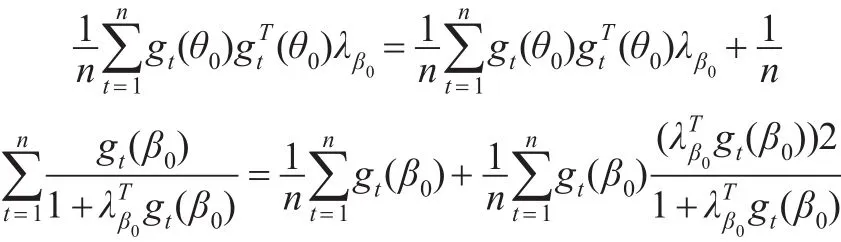
因此有：

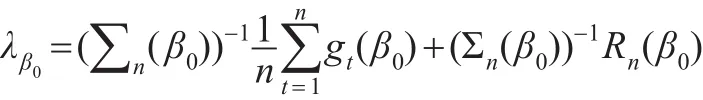
其中：

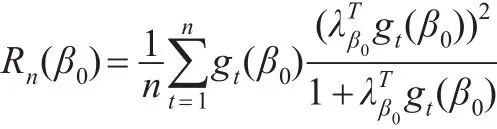
由引理1和2可知：

注意到對(duì)于?t，

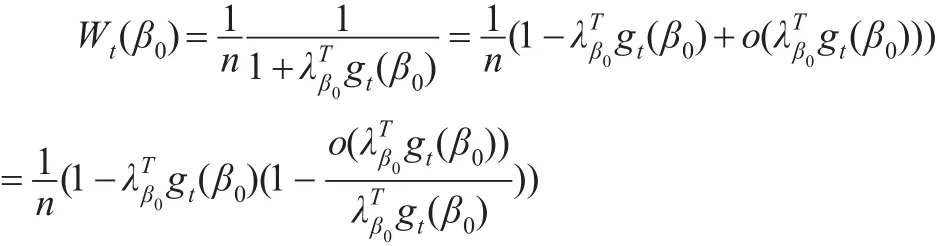
進(jìn)一步由引理1和引理2可知：

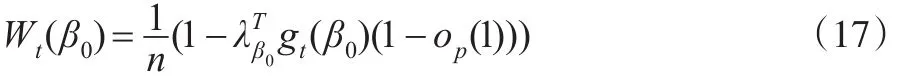
注意到：

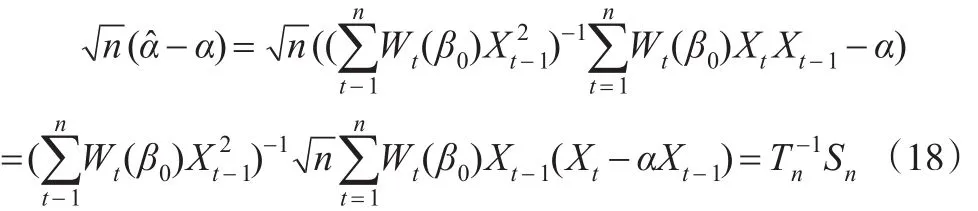
首先考慮Tn，由式（18）可知：

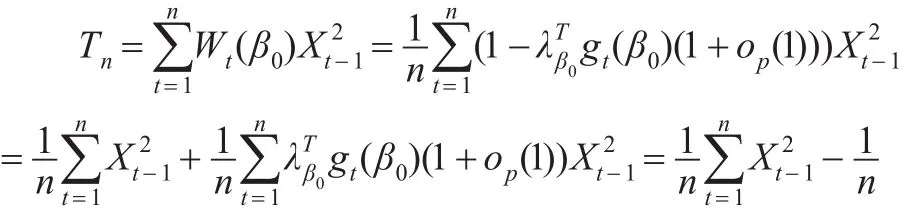
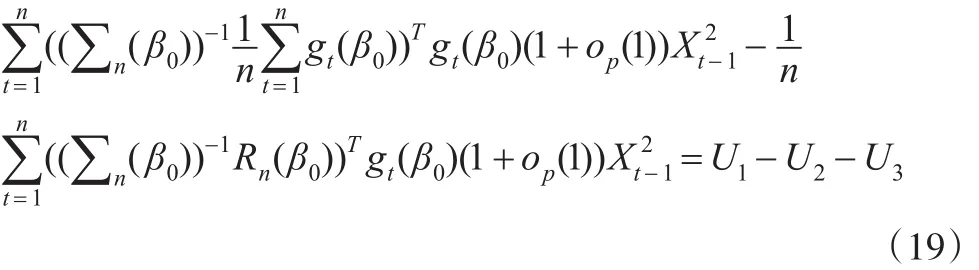
由條件A1和A2以及遍歷性定理可知：

同理可知：

綜合式（19）至式（21）可知：

下面考慮Sn，注意到：

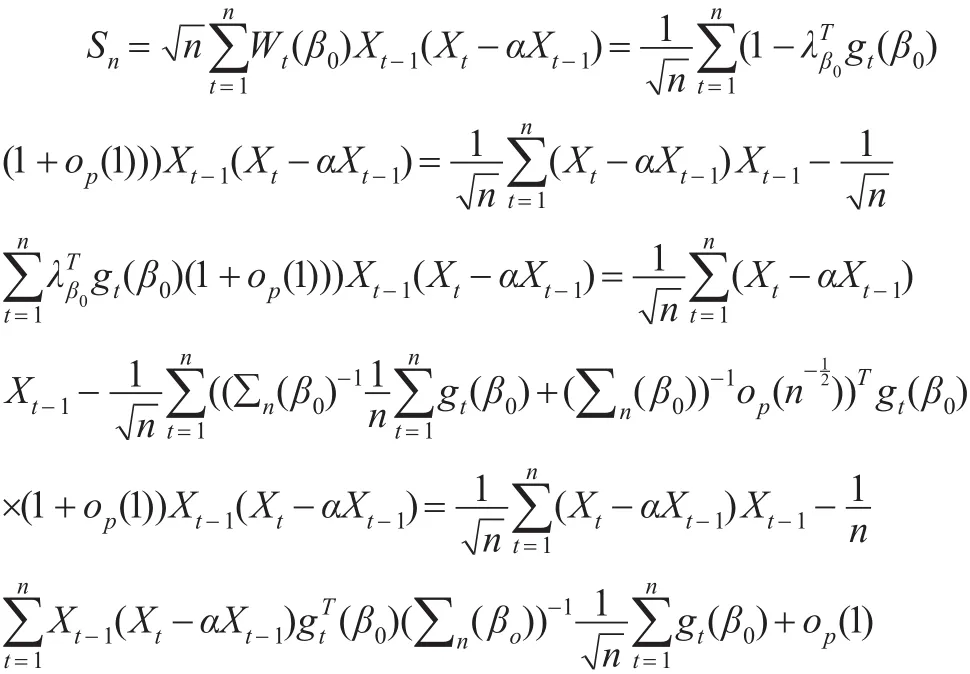
由遍歷性定理可知：

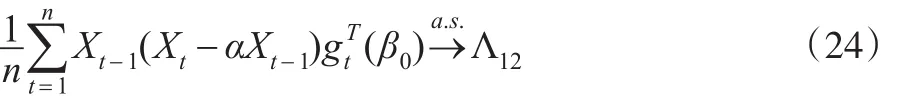
因此由式（10）以及式（24）可知：

由此證明了定理1。

類似定理1的證明，可以證明定理2。

4 結(jié)論

本文主要利用非參數(shù)方法——經(jīng)驗(yàn)似然方法討論了當(dāng)輔助信息可以用條件矩約束表示時(shí)一階自回歸模型參數(shù)的估計(jì)問題。該方法與沒有利用輔助信息的模型參數(shù)的最小二乘估計(jì)相比較，具有更小的漸近方差。因此，有了更多的樣有本信息，得到的估計(jì)具有更高的效果。