競爭風險下右刪失數據的剩余壽命分位數回歸預測
高 偉,馮海林
(西安電子科技大學 數學與統計學院,西安 710126)
0 引言
涉及醫學、工程等領域的可靠性研究中,剩余壽命分位數是做出相關決策的關鍵指標[1],它對壽命分布的尾部特征性依賴性較小,且在偏態分布下具有魯棒性的特點,能較為全面地刻畫分布特征。右刪失數據是一種常見的數據類型[2],具有非對稱和偏態分布性,而剩余壽命分位數對此類數據有較好的表現[3]。競爭風險數據在經典生存分析中極為重要,它由個體面臨失效時間跨度、導致失效的終止事件等多種潛在結局產生,其中潛在終止事件被彼此之間稱為“競爭風險”事件。
在剩余壽命分位數的預測中,由右刪失數據的分位數回歸方法得到的結果較準確。分位數回歸方法被Koenker[4]首次引入,被Ying等[5]、Gelfand等[6]、Wang等[7]進一步推廣;在競爭風險數據類型下,Jeong和Fine[8]進一步提出了對剩余壽命分位數推斷的兩樣本檢驗統計量。但這些方法都忽略了協變量對預測的影響。盡管Jung等[9]在右刪失數據下構建了協變量對剩余壽命分位數影響的半參數估計模型,但其中的協變量被考慮為固定的。實際上,動態協變量對剩余壽命的預測也有顯著影響[10]。目前,尚未有動態協變量對剩余壽命預測影響的研究。
本文基于競爭風險下右刪失數據,建立了剩余壽命分位數回歸模型,得到了剩余壽命分位數和動態協變量之間的函數關系,證明了提出的估計量的漸近性和一致性。數據仿真和實例分析驗證了所提出方法的準確性和有效性。
1 符號和定義
用T表示個體的失效時間,C表示刪失時間,即從觀測開始到個體刪失的時間,令Yi=min(Ti,Ci),定義示性函數 δi=I(Ti≤Ci),用 ε∈(1,2,…,K)表示失效原因,令ηi=δiε=I(Ti≤Ci)ε。通常把影響個體失效時間的重要因素稱之為協變量,記W∈R(p+1)為固定協變量向量,即不隨時間變化,Z∈R(p+1)為與時間相關的動態協變量向量,令U=(W,Z)。假定失效原因為k(k=1,…,K)的累積發病函數為Fk(t|U)=Pr(T≤t,ε=k|U),它表示給定協變量U 時,觀察到失效原因為k的概率。記在t0時失效原因為k的剩余壽命的子分布函數為 Fk,t0(t|U)=Pr(T-t0≤t,ε=k|U,T>t0)。假定給定協變量U時,刪失變量C和(T,ε)是條件獨立的。設G0(t|U)=Pr(C>t,εi=k|U)是刪失分布的條件生存函數。另外,記觀測到的數據為{(Yi,δiεi,Ui),i=1,…,n}。
2 基于動態協變量的剩余壽命分位數建模及其參數估計
基于真實數據的分析表明,剩余壽命分位數與協變量之間的關系一般為對數線性關系[11]。設失效原因為ε=k的剩余壽命τ-分位數和協變量之間的關系是對數線性的,即:
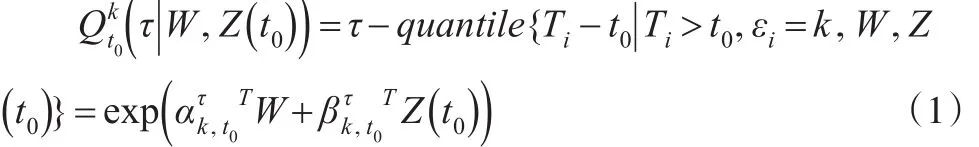
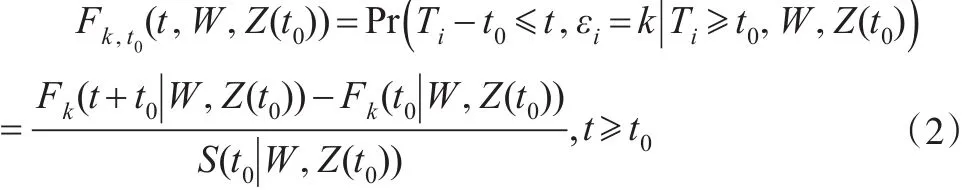
其中 Fk(·)是失效原因為 ε=k 的CIF ,S(·)是所有原因的生存函數。
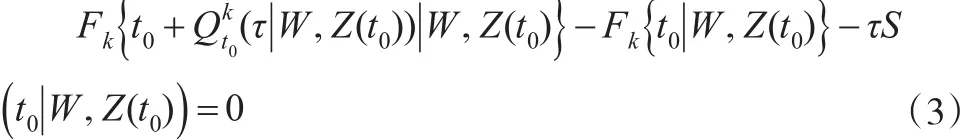
由式(3)得,給定協變量信息下,失效原因為ε=k的τ-分位數函數表示為:
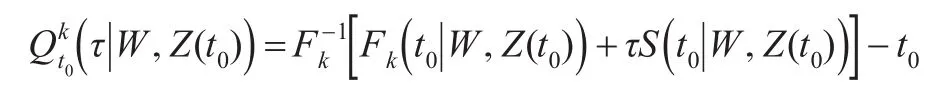
由于在時間t0時τ-分位數函數是CIF在Fk(t0|W,時的逆,因此在t0時,Fk(·)和 S(·)都會影響τ-分位數。令,其中是給定協變量信息時失效原因為ε=k的累積風險函數,ζ即觀測時間的最大值。于是,τ-分位數存在的必要條件是,即ζ,因此t0被約束。
由式(1)和式(3),知:
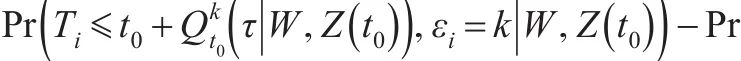
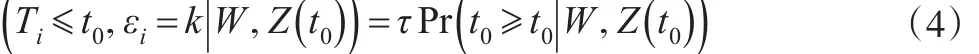
假設 (Ti,εi)和Ci是條件獨立的,則式(4)的左邊第一項等價于:
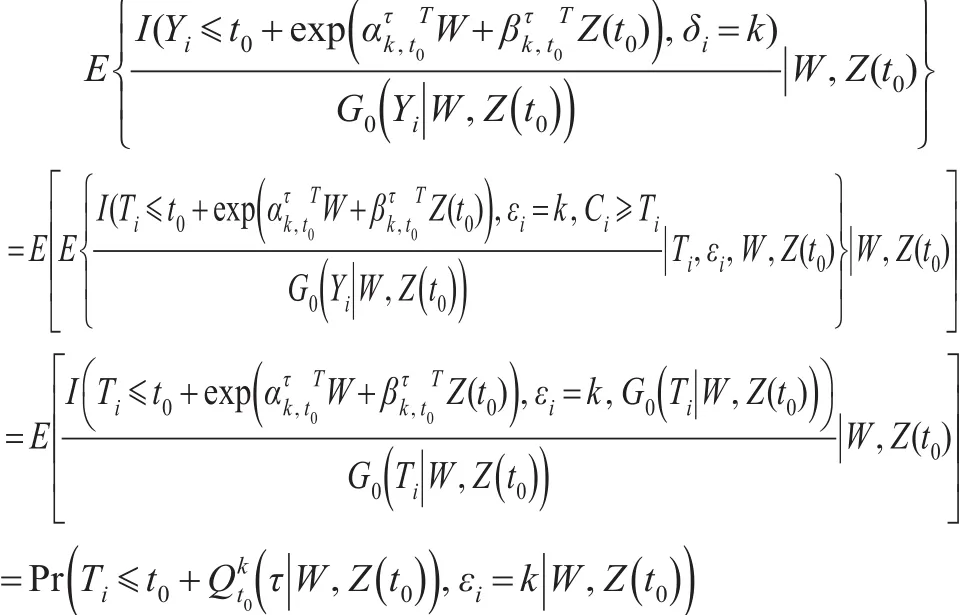
而式(4)的左邊的第二項等價于:
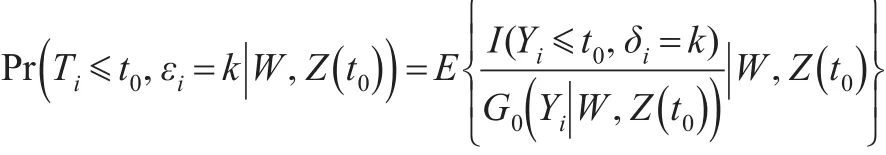
因此,式(4)即為:
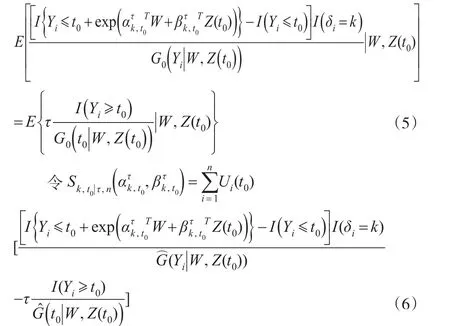
其中G(t|W,Z(t0))是給定協變信息時刪失分布的條件生存函數的Kaplan-Meier估計值[9]。于是:

3 仿真模擬
假設競爭失效原因ε∈{1,2},本文僅對類型1事件感興趣,即ε=1,通過數值仿真來檢驗所提出方法在有限樣本下的表現。考慮一個簡單的情形:
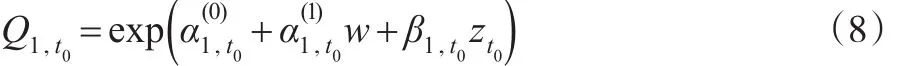
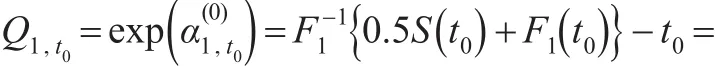
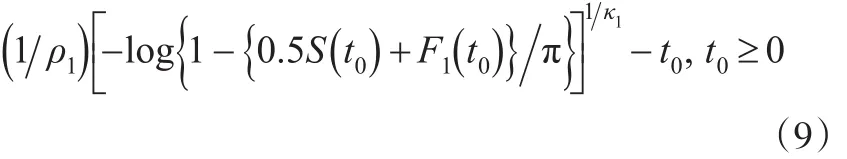
t0=0時假設 ρ2=0.4,κ1=κ2=1.5,。 用產生類型 1 事件的事件時間真值產生類型 2事件的事件時間真值,其中,刪失時間C~UNIF(0,c),其中c為控制刪失比例的常數,觀察到的生存時間Yi=min(Ti,Ci) ,其 中假設 w~Bernοulli(0.5),是不隨時間變化的協變量,zt0是隨著時間變化的協變量,這里采用文獻[10]中的協變量表達式zt0=
本文估計了在刪失比率分別為0、10%、20%、30%的情況下,τ-分位數分別為0.3、0.5且時間t0分別為0、0.5、1、1.5時回歸參數估計的經驗偏差(Bias)、經驗標準差(SD)、平均標準差(SE)和95%Wald型置信區間的經驗覆蓋率(CP)。
表1 t0=0,0.5,1,1.5時,真值回歸參數1.40,1.29和的經驗估計
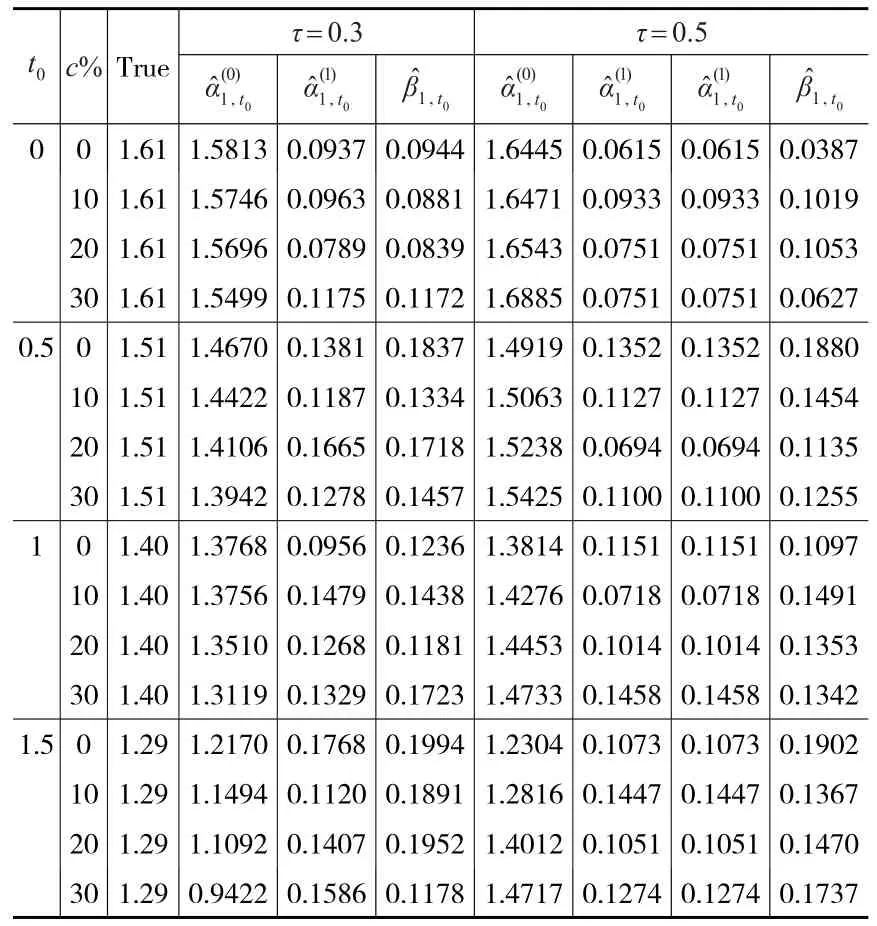
表1 t0=0,0.5,1,1.5時,真值回歸參數1.40,1.29和的經驗估計
注:c%表示刪失比例。
t0 0 c%β1,t0 1,t0 β1,t0 True 1,t0 1.5 1,t0 1,t0 α(1)0.5 0.0937 0.0963 0.0789 0.1175 0.1381 0.1187 0.1665 0.1278 0.0956 0.1479 0.1268 0.1329 0.1768 0.1120 0.1407 0.1586 α(1)10 20 30 0 10 20 30 0 10 20 30 0 10 20 30 τ=0.3 α(0)1.61 1.61 1.61 1.61 1.51 1.51 1.51 1.51 1.40 1.40 1.40 1.40 1.29 1.29 1.29 1.29 τ=0.5 α(0)1 0 1.5813 1.5746 1.5696 1.5499 1.4670 1.4422 1.4106 1.3942 1.3768 1.3756 1.3510 1.3119 1.2170 1.1494 1.1092 0.9422 α(1)1,t0 0.0944 0.0881 0.0839 0.1172 0.1837 0.1334 0.1718 0.1457 0.1236 0.1438 0.1181 0.1723 0.1994 0.1891 0.1952 0.1178 1.6445 1.6471 1.6543 1.6885 1.4919 1.5063 1.5238 1.5425 1.3814 1.4276 1.4453 1.4733 1.2304 1.2816 1.4012 1.4717 0.0615 0.0933 0.0751 0.0751 0.1352 0.1127 0.0694 0.1100 0.1151 0.0718 0.1014 0.1458 0.1073 0.1447 0.1051 0.1274 0.0615 0.0933 0.0751 0.0751 0.1352 0.1127 0.0694 0.1100 0.1151 0.0718 0.1014 0.1458 0.1073 0.1447 0.1051 0.1274 0.0387 0.1019 0.1053 0.0627 0.1880 0.1454 0.1135 0.1255 0.1097 0.1491 0.1353 0.1342 0.1902 0.1367 0.1470 0.1737
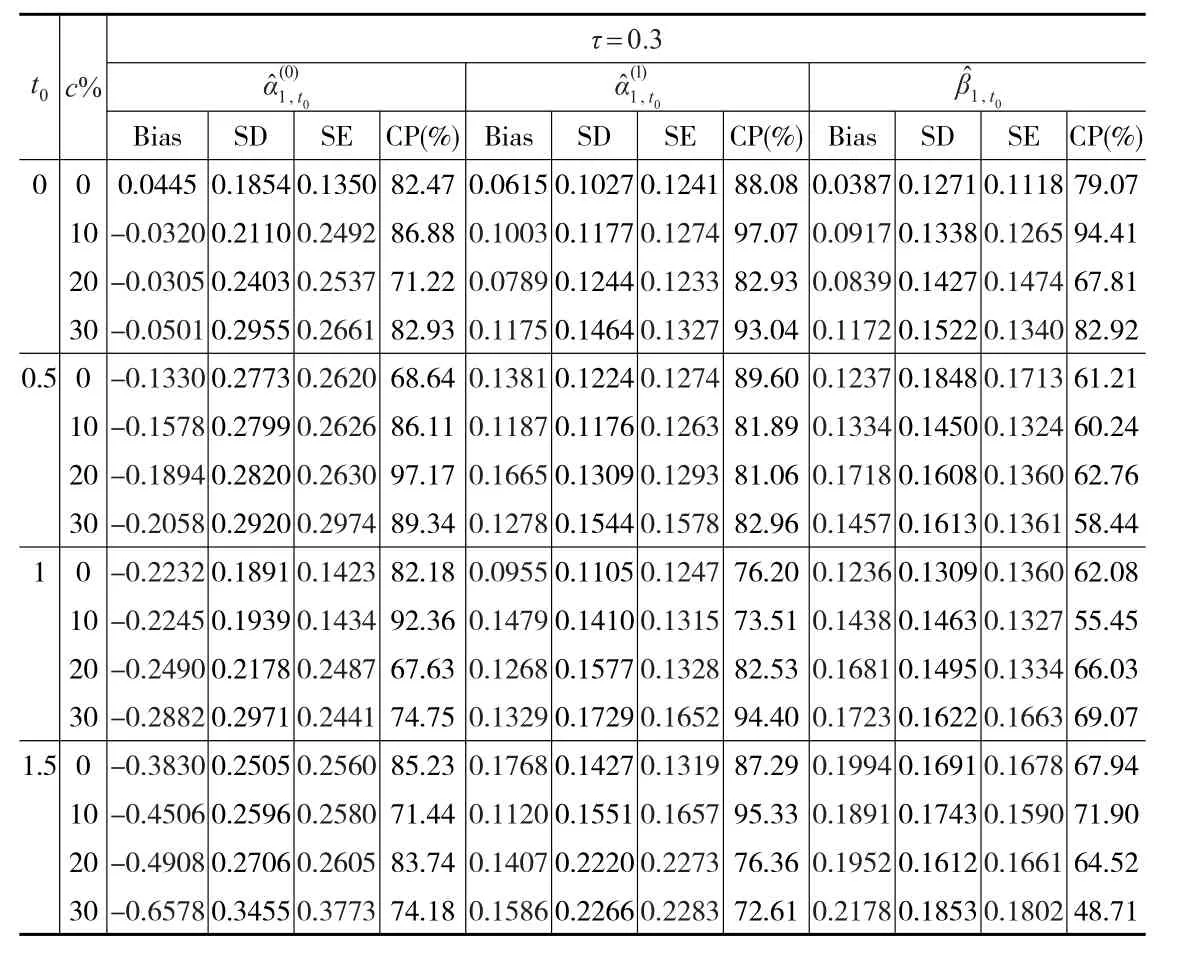
表2 τ=0.3時的Bias、SD、SE、CP
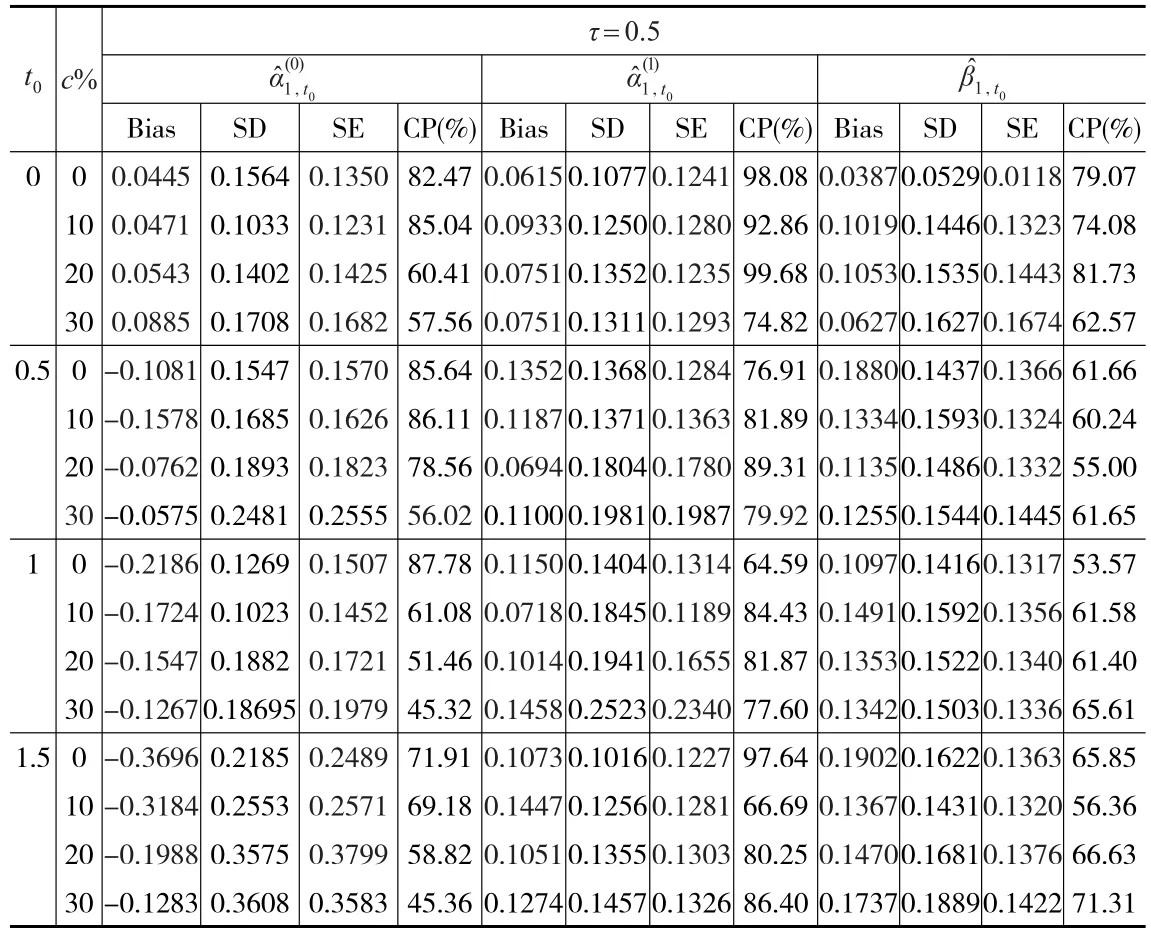
表3 τ=0.5時的Bias、SD、SE、CP
4 實例應用
本文利用美國Channing House數據對所提出的方法進行評估,Channing House是位于美國加利福尼亞州帕洛阿爾托市的一個退休中心,Channing House數據收集并記錄了從1964年至1975年7月1日之間成員的有關數據。在這期間,總共有97名男性和365名女性在該中心生活。此外,所有成員進入和離開退休中心時的年齡也被記錄。根據記錄,發現該數據集屬于右刪失數據類型,因為結束記錄時還有許多成員依舊存活。僅有46名男性和130名女性在研究期間在Channing House退休中心死亡,由此可得刪失率大約為61.9%。
本文感興趣的是成員的性別差異以及進入Channing House退休中心時的年齡和居住持續的時間對生存時間的影響。用w=1表示男性個體,w=0表示女性個體表示人員進入Channing House退休中心時的年齡和居住持續的時間t0。考慮人員的死亡原因為所感興趣的類型1事件,考慮回歸模型對于式(8),在 τ=0.5時利用網格搜索法求解。
表4總結了在t0=0、10、20時的估計值;表5給出參數估計的經驗偏差(Bias)、經驗標準差(SD)、平均標準差(SE)和95%Wald型置信區間的經驗覆蓋率(CP),從這些數據中可以看出,估計值有較好的表現;表6表明了性別差異對剩余壽命分位數的影響,在t0取固定值時,女性比男性生存時間更長;表7列出了考慮動態協變量和未考慮動態協變量條件下的剩余壽命分位數的估計值,可以看出成員進入退休中心的年齡和居住持續的時間對剩余壽命有一定的影響,這與先前的預期是一致的。
表4 在t0=0,10,20時的估計值

表4 在t0=0,10,20時的估計值
t0 01 0 20 τ=0.5 α(0)1,t0 4.1963 4.0020 3.7430 α(1)1,t0-0.3948 0.0655 0.0920 β1,t0 0.2421 0.0492 0.0439
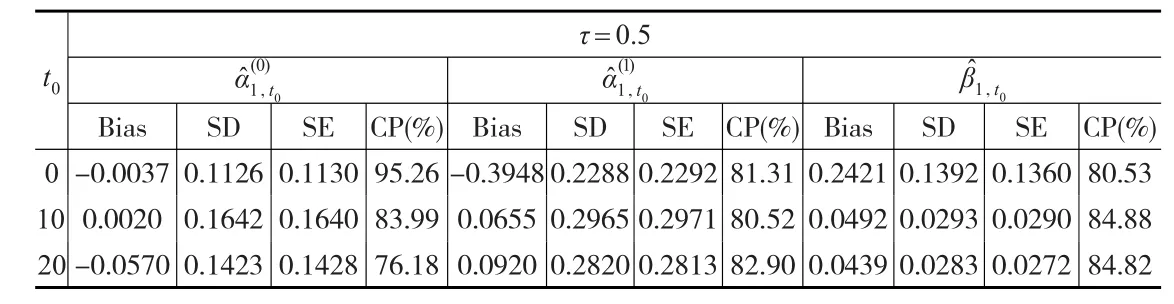
表5 τ=0.5時的Bias、SD、SE、CP

表6 τ=0.5時,性別差異對剩余壽命分位數的影響
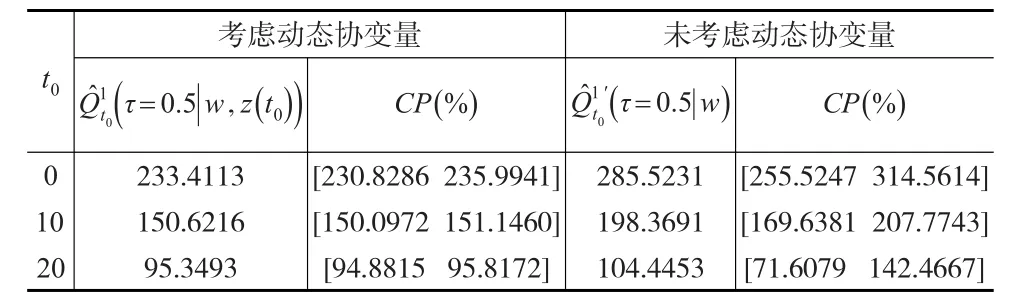
表7 τ=0.5時,兩種情形下剩余壽命分位數的估計值
5 結束語
由于在生物醫學研究領域,生物數據經常是偏態分布的,分位數回歸模型越來越受到研究者的廣泛關注。本文提出在競爭風險下右刪失數據的剩余壽命分位數回歸模型,其主要特點是體現動態協變量與剩余壽命分位數的關系。本文從估計方程中得到估計值,并對其漸進性和一致性進行推導。對模型進行數值仿真,證明提出的估計方法有很好的有限樣本性質。最后,將實際數據集應用于模型,充分體現了動態協變量對于剩余壽命分位數的影響。下一步研究,可以嘗試研究數據類型更為復雜的情況下,動態協變量對于剩余壽命分位數的影響。

