高比轉速軸流泵正交優化設計研究

袁建平， 范 猛， Giovanni Pace， 陸 榮， 李彥軍， 付燕霞

(1. 江蘇大學 國家水泵及系統工程技術研究中心，江蘇 鎮江 212013； 2. Sitael S.p.A., 5 via dellaGherardesca, Pisa 56121, Italy； 3. 江蘇大學 能源與動力工程學院，江蘇 鎮江 212013)

軸流泵廣泛應用于各領域，隨著南水北調和地區灌溉工程的興起，高比轉速軸流泵占據著越來越重要的地位，國內對高比轉速軸流泵模型研制較少，與國外相比效率普遍偏低，拓寬其高效范圍成為目前亟待解決的問題[1-2]。

目前流體機械的優化已有一定的研究[3-6]，試驗設計被廣泛使用并取得了很好的效果。王凱等[7]采用最優拉丁試驗設計對一中比速離心泵的軸面投影圖進行了優化，提高了水力效率。邢樹兵等[8]利用正交試驗設計對軸流泵4組葉輪和導葉進行試驗，得到了最優匹配方案。黃健勇等[9]對斜式軸流泵的進水流道進行了正交優化，有效抑制了小流量下葉輪進口非穩定流態。Kim等[10]將拉丁試驗設計與遺傳算法相結合對一軸流風機進行了多目標優化，提高了風機的整體性能。

軸流式機械的葉輪和導葉的葉片由多個翼型組成，影響葉片形狀的幾何參數多而復雜，目前針對翼型的優化不夠充分。同時，一些學者僅對單一過流部件進行了優化[11-14]，忽視了過流部件的動靜匹配對整體性能的影響[15-16]。

因此，本文基于正交試驗設計方法，針對一比轉速為1 500 r/min的軸流泵的葉輪及其導葉的幾何參數進行了多組匹配方案的設計，同時采用ANSYS CFX14.5對其水力性能展開數值預測，研究各幾何參數對水力性能影響的主次順序，并獲得最佳參數的匹配方案，從而實現對軸流泵的動靜匹配優化。

1 計算模型

本文選取的軸流泵名義比轉速為1 500 r/min，主要性能參數為：設計流量Qd=410 L/s，設計揚程Hd=3.0 m，轉速n=1 450 r/min。其二維結構如圖1所示，主要幾何參數為：葉輪直徑D=300 mm、葉輪葉片數Z=3、輪轂直徑dh=92 mm、葉頂間隙C=0.2 mm、導葉高度H=130 mm、導葉葉片數Zd=5。

圖1 軸流泵的二維結構Fig.1 Two dimensional structural view of the axial-flow pump

采用Creo Parameter3.0軟件對該軸流泵的進出口段、轉輪室和導葉體進行三維造型，為考慮湍流在管內的充分發展，對其進口、出口進行了適當的延伸，如圖2所示。

圖2 軸流泵的三維造型Fig.2 Three dimensional model of the axial-flow pump

2 數值計算

2.1 網格劃分

由于網格的質量和數量對計算結果有重要影響，因此采用ICEM對軸流泵的各計算域選用正交性好、質量較高的六面體結構網格進行網格劃分，葉片表面采用O型拓撲環繞，對壁面進行加密并插入邊界層網格，第一層間距設置為0.2，增長率為1.1，如圖3所示。經網格無關性分析后確定總網格數為3 298 900，各部件網格的詳細信息，如表1所示。

表1 網格無關性分析

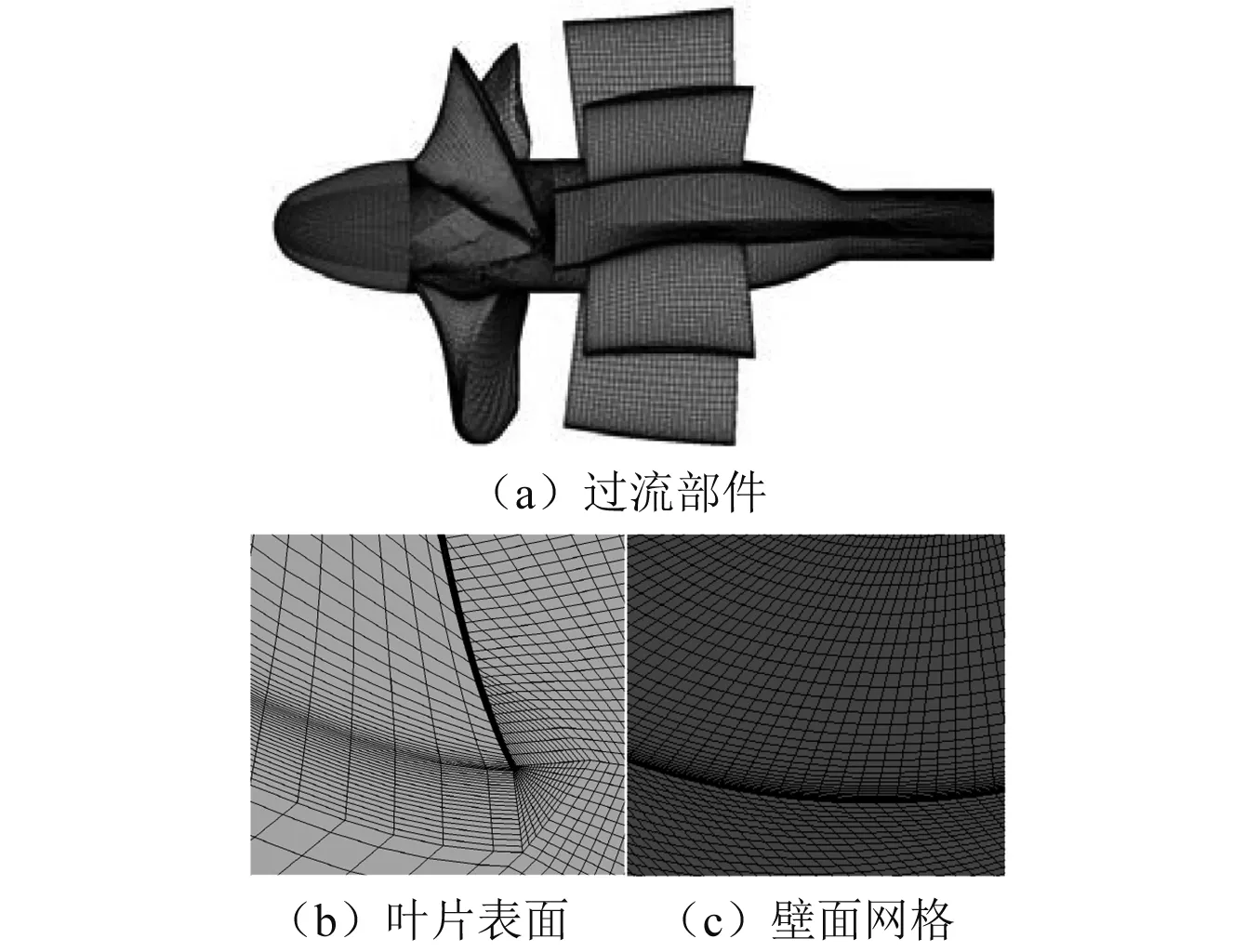
圖3 計算域網格Fig.3 Mesh of the computational domain

2.2 數值方法

為了對軸流泵的內部流動進行數值模擬，基于ANSYS CFX14.5軟件，采用SSTk-ω兩方程湍流模型來封閉動量方程，運用多重旋轉坐標系設置旋轉域和靜止域。進出口的邊界條件分別為總壓進口(1 atm)和質量流量出口。動靜交接面設置為“Frozen rotor”，壁面采用無滑移邊界條件，近壁區利用自動壁面函數處理。求解離散設置為二階迎風格式，物理時間步長設置為1/ω，其中ω為葉輪的旋轉角速度，收斂殘差設置為10-5。

2.3 外特性對比

本次試驗在江蘇大學流體機械工程技術研究中心的多功能大型泵閉式試驗臺上進行，該試驗臺采用立式閉循環水系統，如圖4所示。同時數據采集系統中集成了能量特性、壓力脈動及振動噪聲等測量軟件。該試驗臺效率測量的總不確定度能夠達到±0.36%，高于GB3216/T—2005(1級)、ISO/DIS5198(A級)和SL140-97(±1.3%)的要求。

圖4 多功能閉式試驗臺結構示意圖Fig.4 The schematic diagram of multi-functional closed test rig

由于軸流泵模型體積和運行流量較大，為了減小試驗產生的振動，將轉速設定在1 300 r/min，當進入馬鞍區時將轉速進一步降低至1 000 r/min，通過相似換算得到額定轉速下泵的性能。試驗采用開閥啟動，并且從大流量往小流量逐漸測試，在試驗過程中，始終注意流量和揚程是否穩定，并在最高效率點附近增加數據采集點。

圖5為數值模擬與試驗的水力性能對比(試驗效率值已扣除空載損失)，全流量下兩者的曲線變化具有較好的一致性，小流量下模擬值稍低于試驗值，但最大誤差在5%以內，且葉頂間隙對模擬結果影響不大，因此在優化時為簡化計算模型忽略了葉頂間隙。

圖5 軸流泵水力性能對比Fig.5 Comparison of the hydraulic performances of the axial-flow pump

3 優化方法

3.1 優化因素選取

國內通常采用流線法對軸流泵進行水力設計，但翼型幾何參數及變化規律依賴設計者的經驗修正。為研究主要幾何參數對泵性能的影響，選定從輪緣(Ⅰ)到輪轂(Ⅴ)的5個圓柱展開面作為設計斷面(RⅠ=150 mm、RⅡ=124 mm、RⅢ=98 mm、RⅣ=72 mm、RⅤ=46 mm)，如圖6所示，對軸流泵葉輪和導葉的7個參數進行正交試驗設計，按照經驗范圍每個因素設定為3水平，規定個別參數從輪緣到輪轂按某一規律變化，如表1所示，借助PCAD水力軟件進行參數化設計，葉片選用791翼型設計，導葉采用圓弧法設計。

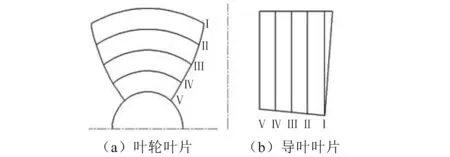
圖6 圓柱面示意圖Fig.6 The schematic view of cylindrical surface

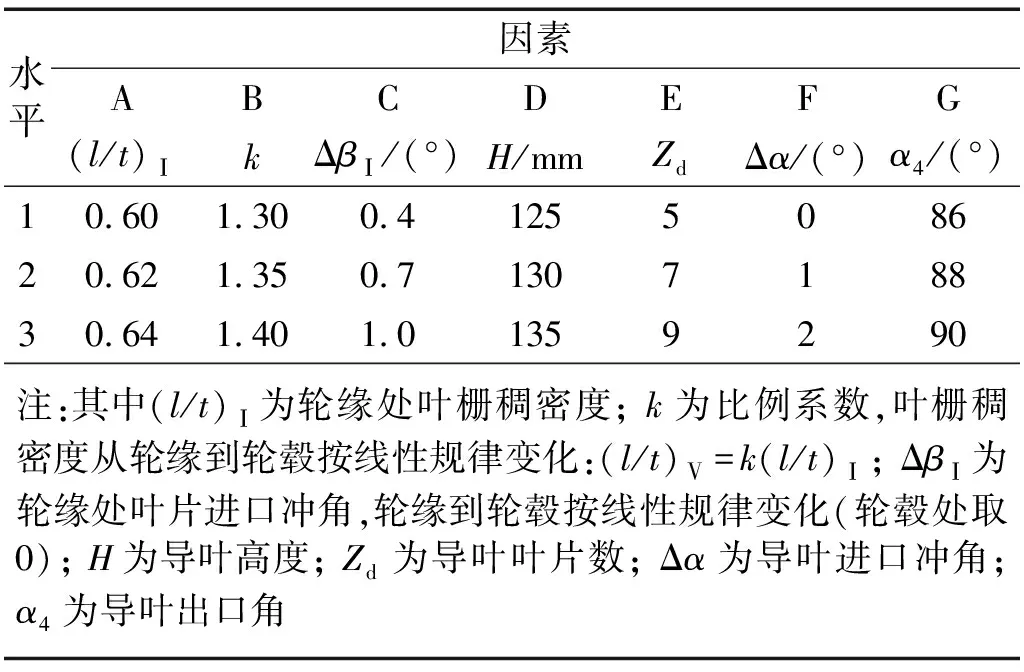
表2 因素水平表

3.2 優化目標

軸流泵的往往需要在多個流量工況下運行，單一工況點的性能提升很難滿足設計要求，為有效地拓寬軸流泵的高效運行范圍，選取了三個流量工況點(0.8Qd、1.0Qd、1.2Qd)的效率(η1、η2、η3)進行優化，以其加權平均值最高為目標，數學模型如下：

求X=[(l/t)Ⅰ,k, ΔβⅠ,H,Zd, Δα,α4]使得

(1)

式中：F(X)為目標函數；ηi(X)為3個工況點的水力效率；ωi為權重因子。權重因子采用層次分析法求得。

首先根據工程經驗假設1.0Qd的重要性是0.8Qd的1.5倍，1.2Qd的1.25倍，1.2Qd為0.8Qd的1.1倍并生成判斷矩陣A

(2)

A中每行元素連乘并開3次方根， 記為

ω*=[0.846 3，1.233 1，0.958 3]T

(3)

歸一化求得權重因子

ω=ω*/(0.846 3+1.233 1+0.958 3)=
[0.278 6，0.405 9，0.315 5]T

(4)

優化目標轉化為

F(X)=0.278 6η1+0.405 9η2+
0.315 5η3→max

(5)

3.3 正交試驗設計

正交試驗利用數學上的“正交性”原理編制標準化的表格-正交表，來科學地安排試驗方案，有效地減少試驗次數[17-18]。本文選取L18(37)正交表列出了18種組合方案，因素水平與參數值對應列出，如表3所示。采用原始方案的數值方法對18種方案進行數值計算，獲取性能參數并進行結果分析。

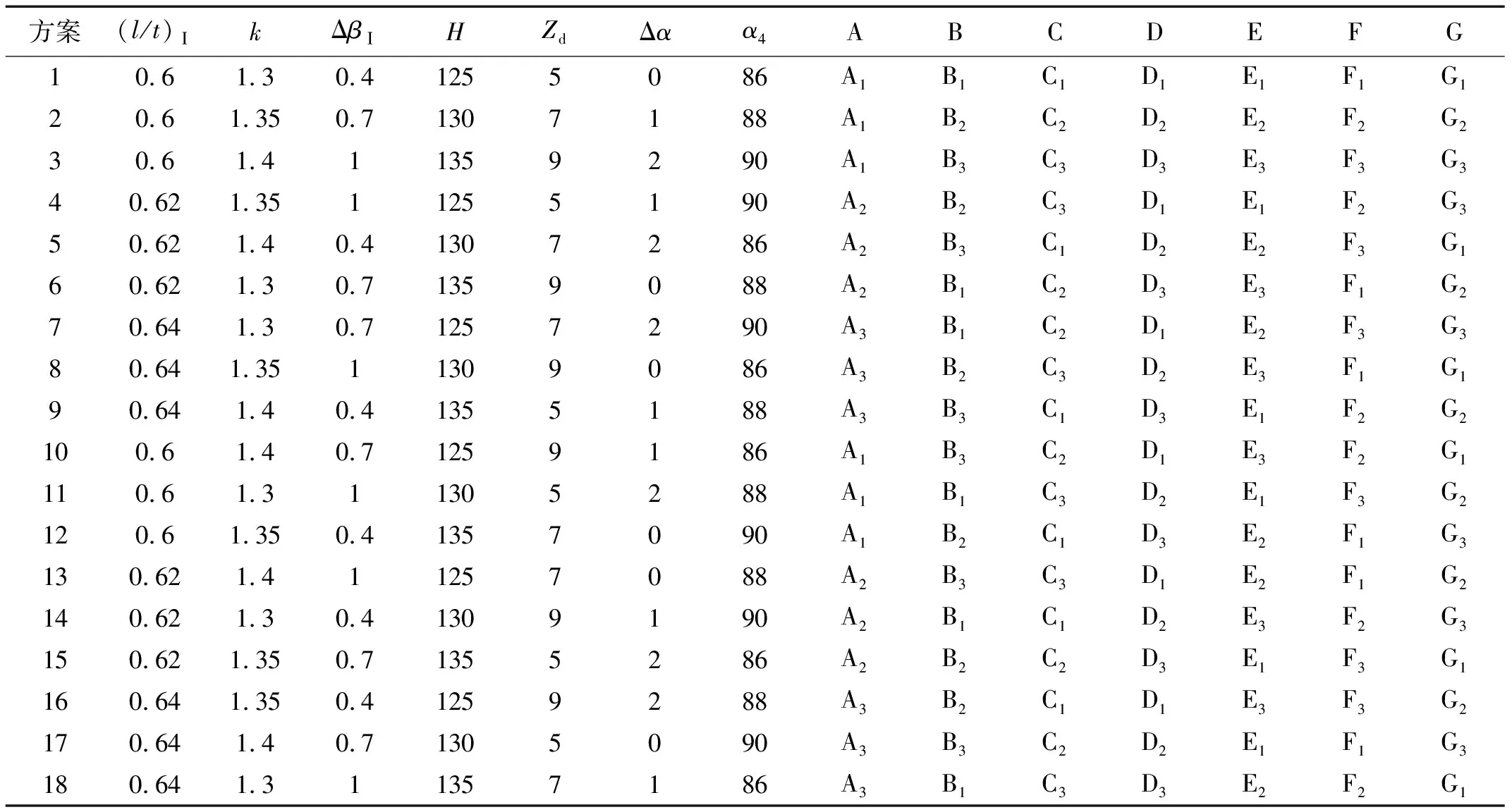
表3 正交試驗方案

4 優化結果

4.1 極差分析

為直觀獲取各因素對目標影響的主次順序，采用極差分析對結果進行處理并獲得各因素的最佳組合。表4為18種方案的計算結果。

表4 數值模擬結果

取各因素在三個水平下目標的平均值作為不同水平對目標的影響結果并計算極差，極差R越大，表明該因素對目標的影響程度越大。以因素A為例，計算方式如下：

k1A=(F1+F2+F3+F10+F11+F12)/6=70.14

k2A=(F4+F5+F6+F13+F14+F15)/6=70.22

k3A=(F7+F8+F9+F16+F17+F18)/6=70.00

RA=max{k1A,k2A,k3A}-min{k1A,k2A,k3A}=0.22

式中： 下標字母A表示因素，數字為該因素對應的水平。各因素的k值和極差如表5所示。各因素對目標影響的主次順序為: C>E>G>A>D>F>B，按k值最大選擇最佳組合為：A2B2C3D1E1F3G3，即(l/t)Ⅰ=0.62、k=1.35、ΔβⅠ=1.0°、H=125、Zd=5、Δα=4°、α4=90°。

表5 試驗結果分析

4.2 外特性試驗對比

按照最優組參數合進行設計水力設計并加工成樣機，在江蘇大學流體機械質量技術檢驗中心的閉式試驗臺上對其進行外特性試驗驗證，如圖7所示。試驗方法參照GB/T 3216—2005《回轉動力泵水力性能驗收試驗1級和2級》的相關規定，試驗滿足2級精度。

圖7 樣機及試驗裝置Fig.7 Prototype and test equipment

優化前后泵的幾何及性能參數變化如表6所示，優化后0.8Qd、1.0Qd和1.2Qd的效率分別提高了1.74%、3.62%和9.67%，目標值加權平均效率提高了4.68%。對比全流量性能曲線發現：大流量下效率提高較為顯著，小流量下效率幾乎不變，全流量下揚程略有增加，但設計點揚程幾乎不變，高效范圍得到一定拓寬，如圖8所示。

表6 優化結果對比

圖8 優化前后水力性能對比Fig.8 Comparison of the hydraulic performances before and after optimization

4.3 內流特性對比

為對比優化前后泵的內流特性，選取了葉輪和導葉內70%、80%和90%葉高處圓柱展開面的湍動能分布及速度流線分布圖，如圖9所示。湍動能是衡量湍流在時間和空間上發展或衰退的指標，也是流動穩定性的標志。對比發現：優化后小流量下湍動能分布變化不大，導葉流道內湍動能有所減小；優化前設計流量下導葉背面存在高強度湍流集中區，而優化后導葉流道內湍動能幾乎較小為0且分布更加均勻；大流量下優化效果最為明顯，優化后從葉輪進口至導葉出口均未出現較強的湍流區域，流動十分穩定。

圖9 葉輪導葉內湍動能對比Fig.9 Comparison of the turbulence kinetic energy before and after optimization

如圖10所示，優化前后三個工況點葉輪流道內均未出現明顯的流動分離，整體流態較好。相比于葉輪流道，導葉流道內則出現了較為明顯的流動分離，其中小流量工況下導葉流道內及出口處的流動分離最為顯著，在各葉高處四個流道內均出現大尺度的分離漩渦，主要集中于導葉葉片背面；導葉出口流體速度很大程度上偏離導葉出口角，流態十分紊亂。最優工況和大流量工況下導葉流道內流線基本貼合葉片型線，而在導葉出口存在不同程度的流動分離，使得導葉出口流體速度方向不同程度地偏離軸向。優化后小流量工況下導葉流道內的流動分離依然存在，但整體流態有了一定的改善；大流量下優化效果尤為明顯，優化后各葉高處導葉背面未出現流動分離，而導葉工作面流線開始偏離型線，局部出現流動分離；導葉出口流態較優化前有很大的改善，其出口速度更加均勻，流體幾乎沿軸向流向出口。優化后葉輪與導葉的匹配性能更佳，流道內的水力損失減小，提高了水力效率。

圖10 不同葉高處的流線對比Fig.10 Comparison of streamline at differentspans before and after optimization

5 結 論

本文基于正交試驗設計方法，針對一比轉速為1 500的軸流泵的葉輪及其導葉的幾何參數進行了多組匹配方案的優化設計，同時采用ANSYS CFX14.5對其水力性能展開數值預測，并與其相應的實驗結果進行對比，得到以下結論：

(1) 基于參數化水力設計、CFD和正交試驗設計對軸流泵葉輪和導葉設計了18組匹配方案，實現了對軸流泵的快速優化，縮短優化周期，節約成本。

(2) 通過極差分析確定其對效率影響的主次順序，其中葉片外緣進口沖角、導葉葉片數和導葉出口角對效率的影響起主要作用。

(3) 通過參數擇優組合，得到優化模型。經樣機試驗，優化后3工況點的加權平均效率提高了4.68%，大流量下效率提升最為顯著，同時內部流動得到明顯改善。說明葉輪與導葉的動靜匹配對軸流泵水力性能影響較大。