土壤膨脹性對降雨入滲產流影響試驗
邵麗媛,甘永德,蘇輝東,3,賈仰文,張海濤,趙思遠,鄭柏楊
(1.河北工程大學水利水電學院,河北 邯鄲 056000; 2.中國水利水電科學研究院 流域水循環模擬與調控國家重點實驗室,北京 100038; 3.清華大學水利水電工程系,北京 100084)
0 引 言
膨脹性土壤在全世界有廣泛的分布,土壤膨脹性對工程建設、生態保護、農業種植和社會經濟都有嚴重的破壞作用[1,2]。在自然條件下,膨脹性土壤會發生周而復始的吸水膨脹、失水干縮的干濕交替過程。由于其結構穩定性差,強烈的濕脹干縮作用產生的壓力和應力的變化會使膨脹性土的受力和形態發生改變[3-5]。降雨入滲產流是水循環的重要組成部分,而土壤膨脹性會影響降水在陸面水文循環入滲過程[6,7]。土壤脹縮變化是一個復雜的過程,主要受到膨脹力和自重應力的影響。其中膨脹力的大小隨土壤含水量變化而變化,自重應力會因土壤深度變化而變化,導致土壤受力變形特征會隨著土壤深度的增加而發生改變,所以導致土壤水分運動參數和入滲特性等變化,使土壤入滲過程變得復雜。
非飽和帶多孔介質中的土壤水分運移研究是目前研究的熱點和難點,目前研究主要集中在分層土壤、空氣阻力、土石混合介質等對土壤入滲產流的影響[8-11],而有關膨脹性土降雨入滲的研究偏少。仇榮亮等[4]對變形土的膨脹收縮特點進行了研究,也表明土壤的脹縮潛力必須借助于干旱交替才得以表達,但沒對膨脹性土壤入滲過程進行描述。呂殿青、邵明安等[13-15]通過實驗研究,測定五種收縮特征曲線,著重描述了土壤收縮特征,只對收縮特征指標和土壤物理學特性間的關系研究。而黃傳琴等[16]探討在干濕交替過程中膨脹性土壤的脹縮特征,通過研究土壤脫水收縮和吸水膨脹過程中比容積與含水量的關系,采用三直線模型[17]擬合土壤脹縮過程,不過主要也是針對膨脹性土壤的收縮、膨脹過程進行分析。甘永德等[18,19]更是建立膨脹性土壤的土壤水分運動參數計算模型,量化了膨脹變形對入滲產生的影響,進一步提出了考慮土壤膨脹性非穩定降雨入滲產流模型(GJGAM),擬合結果較好,但都沒有針對膨脹性土壤的入滲產流過程進行描述。而劉春成等[20]對斥水土壤的入滲規律進行四種入滲模型擬合探討其適用性;司曼菲等[21]只擬合了在土石混合介質碎石情況下土壤入滲過程,然而膨脹性介質導致的土壤參數變化、入滲曲線的影響沒有研究。
基于以上研究,本文主要針對膨脹性土壤開展了室內不同厚度土壤降雨入滲產流實驗以及土壤水分運動參數測定,研究分析降雨入滲條件下土壤容重變化情況,土壤累積入滲量和入滲強度隨時間變化關系;并采用Philip公式、Kostiakov公式和Horton公式分別對土壤入滲過程水分運動曲線擬合。本文主要研究目的:①研究土壤膨脹性在降雨條件下對土壤參數變化的影響;②尋找最適合擬合膨脹性土壤的特征水分運動曲線的方法,能夠正確描述土壤膨脹性在降雨條件下影響入滲的經驗模型。相關研究可以促進對膨脹性土壤水分入滲過程的認識,豐富多孔介質土壤水運動規律。
1 試驗材料與試驗設計
1.1 試驗材料
本次試驗采用兩種典型膨脹性土壤——黃綿土和婁土,這兩種土壤皆是黃土高原常見的土壤,由于水土流失地表土層沖刷黃土暴露后耕種而成。其中婁土是自然褐土基礎上經過人類長期耕作熟化的耕作土壤,主要分布于陜西關中盆地及渭河,質地多為中壤至重壤,通透性較好;黃綿土是由黃土母質經直接耕種而形成的一種幼年土壤,是黃土高原面積上最大的農業土壤,疏松軟綿,通透性較好。其基本理化性質如表1所示。風干后過5 mm篩備用,其風干后備用的土壤初始含水量見表2。

表1 土壤基本物理性質Tab.1 Fundamental soil physical property
注:試驗采用吸管法測定土壤顆粒組成,比重瓶法測量土密度,恒體積法測飽和導水系數。
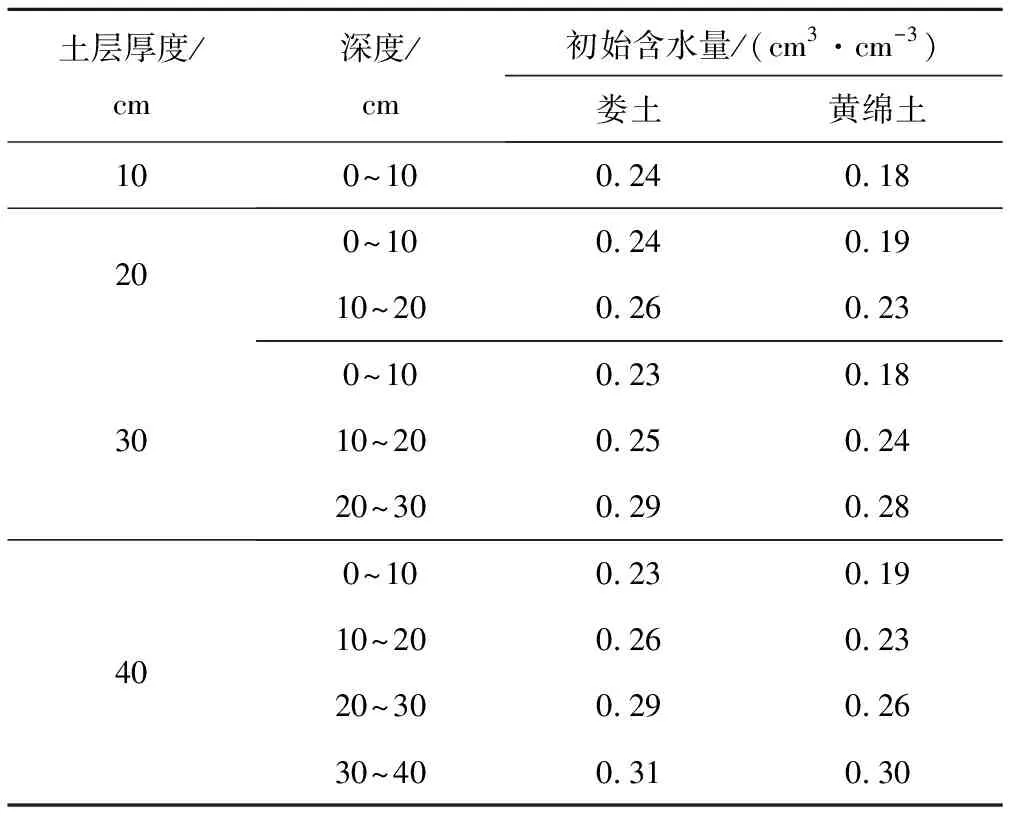
表2 土壤初始含水量Tab.2 The initial soil moisture content
1.2 試驗設計
膨脹性土壤吸水膨脹變形主要受膨脹力和自重應力影響,導致土壤入滲過程隨著土壤深度的變化而變化。為了定量分析膨脹性土壤對土壤降雨入滲產流過程影響,試驗設置4個厚度,分別為10、20、30、40 cm,每個處理兩個重復,分別標記為:婁土10 cm、婁土20 cm、婁土30 cm和婁土40 cm。
試驗時,將經5 mm篩的土壤分層(10 cm)均勻裝入土槽中,土壤裝填過程中嚴格控制了土壤容重,因此吸水變形前土壤剖面密度相同,因此密度變化只能發生在注水以后和降雨過程中吸水膨脹變形。土壤吸水膨脹變形首先導致土壤顆粒體積變化,進而導致孔隙度變化。土壤吸水變形后土層厚度均發生變化,對此我們采用土柱法針對性測定了土壤飽和水分運動參數試驗。土槽中間位置深度0、10、25、40 cm處安裝Trime水分傳感器,用以測定土壤水分動態過程。土槽設置兩個出水口,分別為壤中流和地表徑流。土壤裝填時,首先在土槽底部鋪設反濾作用的石子,厚10 cm;再在石子的上面鋪設紗布,然后將過5 mm篩后的土壤按定密度(1.4 g/cm3)裝入土槽。
試驗進行前,向土槽注入足夠水量(土壤達到田間持水量以上,并產生大量壤中流)后靜置,待其膨脹量達到相應土壤含水量最大膨脹量后進行降雨試驗。
試驗過程中,用降雨系統進行人工降雨,每次降雨歷時控制在350 min左右。試驗中Trime水分測定系統記錄水分動態。同時,對地表徑流量、壤中流流量進行收集、量測。徑流觀測時間間隔,根據產流速度而定,由于壤中流退水較慢,因此加長相應觀測時間,假如試驗過程中不產生壤中流,則放棄測定。試驗設置1個雨強,30 mm/h,1個坡度,5°。
試驗主要觀測資料:徑流(地表徑流量、壤中徑流量)、土壤剖面水分動態、產流歷時、降雨強度等。
2 試驗結果與討論
為了分析土壤膨脹性對降雨入滲產流的影響,根據試驗結果,對比分析黃綿土和婁土這兩種典型膨脹性土壤的土壤容重、土壤累積入滲量和土壤徑流強度變化規律。
2.1 土壤容重隨深度變化關系
降雨入滲試驗后可測定土壤的干密度,研究發現土壤不同剖面的土壤密度發生了變化(表3)。黃綿土和婁土在各種厚度的膨脹性土壤受到膨脹力和重力雙重作用均導致表層0~10 cm土壤平均干密度相對減小,10 cm以下深度土壤干密度隨深度增加而相對增加。原因在于膨脹性土壤飽和后的土壤容重在土體自身重力和土壤膨脹力的共同作用下發生了改變。
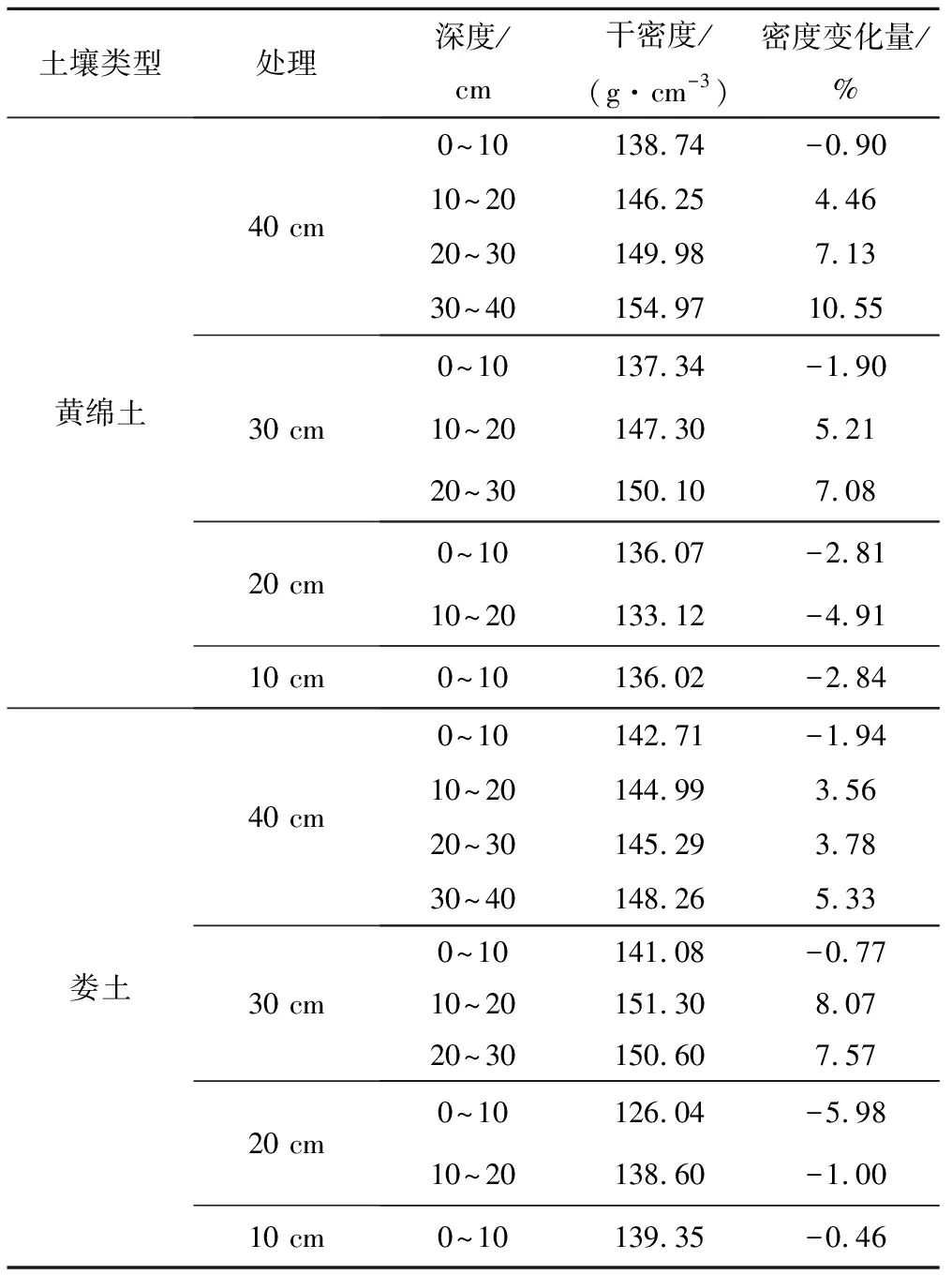
表3 土壤容重隨深度變化統計表Tab.3 Changes of soil bulk density with depth
2.2 土壤累積入滲量隨時間變化關系
黃綿土和婁土的土壤累積入滲量隨時間變化關系如圖1所示。土壤累計入滲量都隨時間單調增大,且厚度越大累積入滲量越小。考慮是因土壤具有膨脹性,入滲過程中受到了土壤膨脹力和自重應力共同作用。深度較小時,主要受膨脹力導致孔隙度增加,導水率增加;隨著土壤深度的增加,土壤自重應力占主導作用使土壤容重增大,孔隙度減小,土壤入滲率減小。相同條件下對比黃綿土,婁土的黏粒含量要高一些,導水系數較小,導致婁土的累積入滲量較小。
2.3 土壤徑流強度隨時間變化關系
徑流強度隨時間變化關系(圖2)可以看出,不同土壤試驗組中,初始入滲時間內徑流強度變化很大,隨入滲歷時的逐漸增加,土壤徑流強度也會逐漸增大,然后趨向穩定。而且對于不同土壤類型來說,如黃綿土的淺層土土壤顆粒較穩定,前期入滲的徑流強度波動較小;婁土的深層土壤顆粒較穩定,在徑流強度趨于穩定后波動幅度較小。當然,不同處理間相同時間時段內徑流強度大小與降雨強度、入滲強度等也有密切關系。試驗期間降雨系統具有一定不穩定性,有可能導致每次降雨強度出現一定偏差,進而導致地表徑流強度規律出現一定混亂。
3 土壤特征水分運動曲線擬合
土壤降雨入滲產流過程中,對黃綿土和婁土不同厚度實驗組采用Philip公式、Kostiakov公式和Horton公式進行土壤特征水分運動曲線擬合,對三種公式擬合結果精度加以分析。
3.1 Philip公式擬合結果
進行降雨入滲實驗的過程中,土壤水入滲速率可以明顯分為兩個階段:
(1)
式中:t1為土壤達到飽和所需時間,min;P為降雨強度,cm/min;S表示土壤吸濕率;A表示穩定入滲率。
Philip公式應用了MATLAB進行擬合,可以定量分析入滲過程中入滲時間和入滲率之間的關系(表4)。
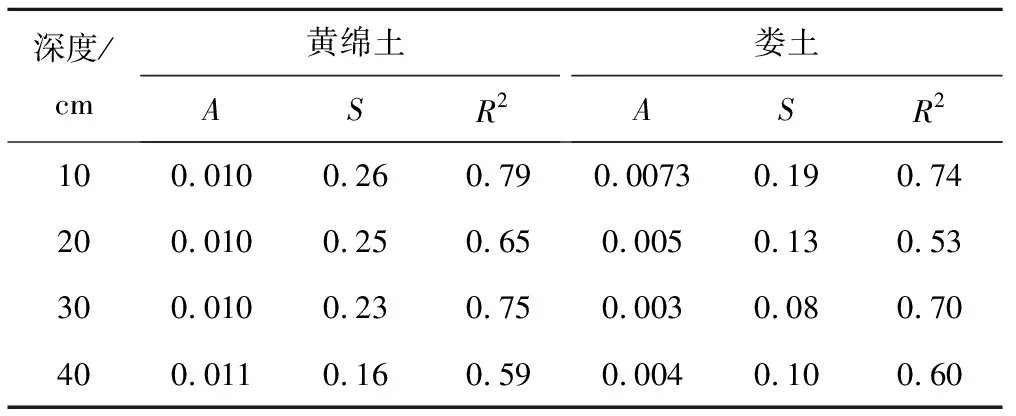
表4 Philip公式擬合結果Tab.4 Fitting result of Philip model
可以看出R2都在0.6左右,擬合效果一般,由實測數據擬合來看,Philip公式可以考慮應用在當忽略吸水時上層土體產生的壓力水頭或土壤吸水過程中所受重力。隨著滲入時間的增大,膨脹土的入滲速率減慢,累積入滲量增加,而土壤吸水能力減弱。不同深度黃綿土的穩定入滲速率基本上不隨深度變化而變化,婁土的穩定入滲速率會隨深度的增加而減小,土壤入滲速率趨于平緩。擬合土壤入滲速率大都較高于實測土壤入滲速率,初步考慮是受膨脹性土壤入滲時體積變化,導致孔隙率增大,進而飽和含水量增大的影響,最后土壤吸力會減弱。
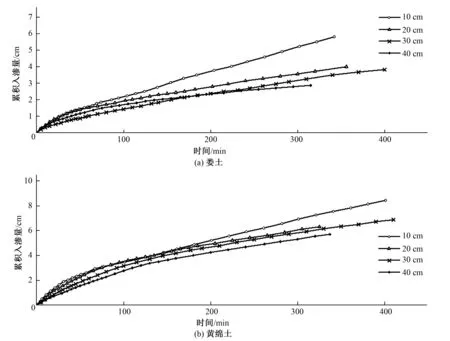
圖1 土壤累計入滲量隨時間變化關系Fig.1 Cumulative infiltration changed over time
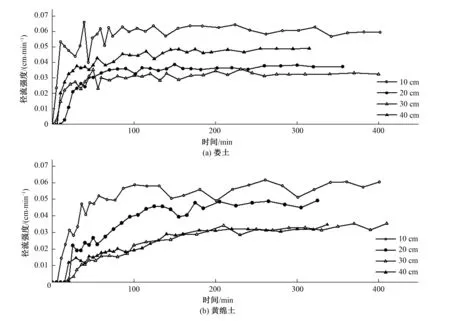
圖2 徑流強度隨時間變化關系Fig.2 The runoff intensity changed over time
3.2 Kostiakov公式擬合結果
在土壤水入滲過程中,Kostiakov公式可以看出土壤水累積入滲量隨時間變化的趨勢。入滲方程可以表示為:
(2)
式中:H為累積入滲量,cm;t為入滲時間,min;k為經驗入滲系數,cm/min,表示入滲開始后第一個單位時段內的累積入滲量;α為土壤經驗入滲指數,無量綱;f0為穩定入滲率,cm/min。
對上式求導,可得到入滲速率的表達式:
f=at-b+f0
(3)
式中:參數a可以用來描述入滲過程中時刻t時的入滲速率和穩定入滲速率的差值,參數a主要受穩定入滲速率f0的影響。
Kostiakov公式應用MATLAB擬合土壤水的入滲過程,擬合結果見表5。
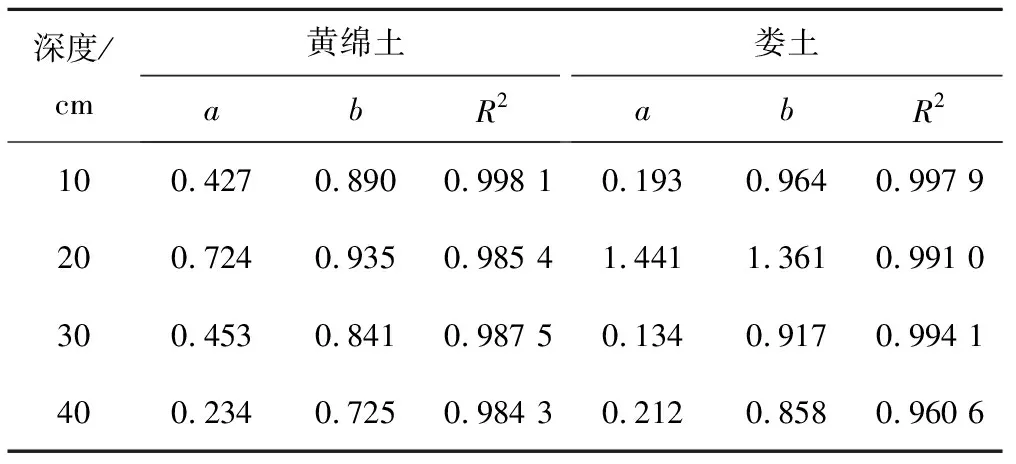
表5 Kostiakov公式擬合結果Tab.5 Fitting result of Kostiakov model
由擬合結果看出,擬合過程中深度增加時,R2減小,但是Kostiakov公式整體擬合效果較好。飽和時的穩定入滲速率和初始入滲速率會對Kostiakov公式產生影響,而膨脹土吸水導致的體積變化對這兩個值無大影響,所以Kostiakov公式的擬合情況較好。
3.3 Horton公式擬合結果分析
Horton公式考慮也分為兩部分計算:
(4)
式中:P為降雨強度,cm/min;i0為t=0時的初始入滲率;ir為穩定入滲率;β為描述入滲過程中速率的減慢程度。
Horton公式的擬合結果見表6。在Horton公式擬合結果中,由參數β變化趨勢看出,對于不同土壤來說,入滲速率都是隨深度變化先減后增。而婁土的參數β值都比黃綿土的大一些,由此可以得出相同深度情況下婁土的入滲速率變化要快于黃綿土的。
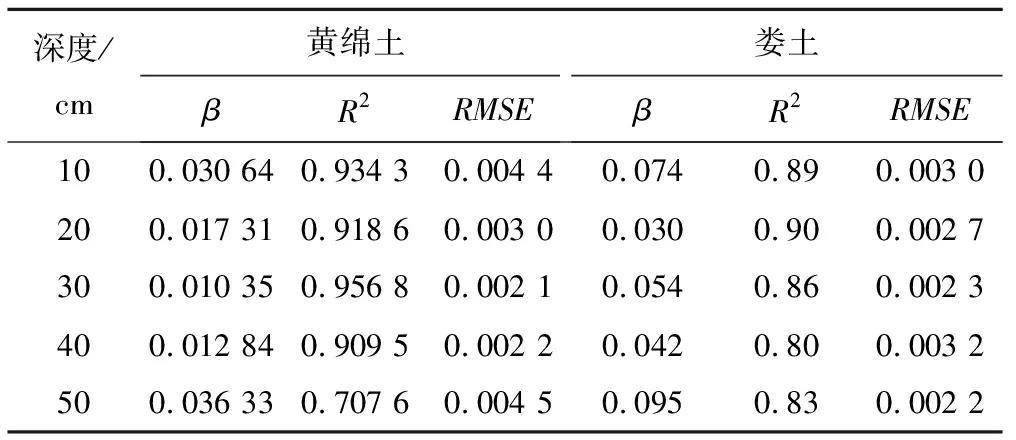
表6 Horton公式擬合結果Tab.6 Fitting result of Horton model
對于Horton公式的擬合,R2整體隨深度變化呈減小趨勢,即對淺層變形較小的土壤擬合效果較好,對深層變形較大的土壤擬合效果則較差。黃綿土的膨脹孔隙率小于婁土的,體積變化率也較小,其R2也較高,則考慮土壤類型和土壤體積變化對Horton公式擬合有一定的影響。
3.4 擬合結果討論
對比Philip公式、Kostiakov公式和Horton公式擬合情況(圖3、圖4),根據擬合結果,可以得出以下結論:①Philip公式只考慮土壤水的入滲速率僅與時間有關,擬合效果較差。而Kostiakov公式的擬合值與實測值最為相近,適合應用于降雨入滲模型。②Kostiakov公式和Horton公式的擬合效果都很接近于1。但是入滲速率存在差異,其中Kostiakov公式只考慮穩定入滲率隨時間的變化關系,而Horton公式還把在土壤飽和過程中土壤水入滲速率的變化程度納入考慮范圍。由此可以看出Kostiakov公式更適合應用于土壤飽和段的擬合,Horton公式適用于初始入滲至穩定入滲的過程,是考慮膨脹土體積變化的土壤水分特征曲線擬合的模型。
本文主要對黃綿土和婁土兩種土壤類型不同厚度試驗組進行試驗,而采用擬合的3種模型模擬結果顯示黃綿土的相關系數R2大部分高于婁土的,其主要因由是在入滲過程中黃綿土吸水膨脹率要小于婁土的,受到了土壤的水分特征參數影響(不考慮誤差)。
4 結 語
本文是在積水入滲試驗的基礎上,對黃綿土和婁土這兩種典型膨脹性土壤進行室內降水入滲試驗,試驗計量出膨脹性土壤在降雨入滲產流下的各參數動態變化。可得出以下結論:①在土壤降雨入滲過程中,膨脹性土壤會吸水膨脹變形,使土壤受到其自身重力還有膨脹力的共同作用,導致土壤容重發生改變。②相同入滲時間內,土壤厚度越大,土壤累計入滲量會越小,但是大小幅度會受到土壤類型不同、土壤入滲位置和降雨強度等影響。③降雨入滲試驗過程中,Horton公式適用于初始入滲至穩定入滲的過程,Kostiakov公式適合應用于降雨入滲模型土壤飽和段的擬合,而 Philip公式并不適合降雨條件下膨脹性土壤水分入滲特征曲線擬合。
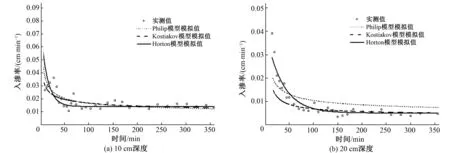
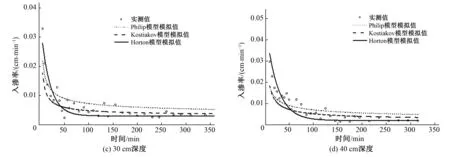
圖3 婁土土壤水分特征曲線擬合結果圖Fig.3 Schematic of the fitting result of each model for Lou soil
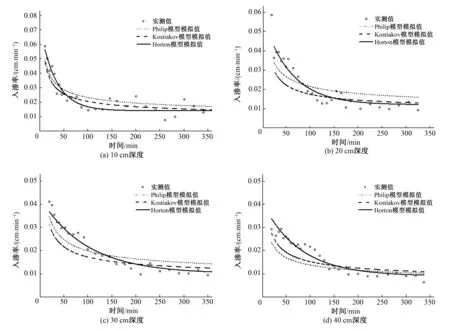
圖4 黃綿土土壤水分特征曲線擬合結果圖Fig.4 Schematic of the fitting result of each model for loessal soil
□

