四旋翼飛行器建模、仿真與PID控制

北京航空航天大學自動化科學與電氣工程學院 陳聽雨

四旋翼是一種實用的無人飛行器。本文首先對四旋翼進行了動力學分析，在其基礎上建立了四旋翼的數學模型。在對模型進行化簡后，設計了飛行控制系統，并將控制系統拆分為內環姿態控制與外環位置控制，分別設計了PID控制率對其進行控制。最后在Matlab/Simulink中搭建了完整的四旋翼飛行控制仿真模型，并對模型與控制率進行了仿真驗證。

1.引言

四旋翼飛行器是一種能實現垂直起降的非共軸式多旋翼飛行器（李俊,李運堂.四旋翼飛行器的動力學建模及PID控制[J].遼寧工程技術大學學報(自然科學版),2012,31(1):114-117）。小型四旋翼飛行器具有四個螺旋槳，并且螺旋槳呈十字交叉結構的旋翼式飛行器，它通過調整四個電機的轉速來實現俯仰、橫滾、偏航等飛行動作，并具有可懸停、機動性好、結構簡單等優點（江杰,豈偉楠.四旋翼飛行器建模與PID控制器設計[J].電子設計工程,2013,21(23):147-150）。

圖1 四旋翼飛行器

與固定翼飛行器相比，四旋翼控制相對簡單，只需調節其四個旋翼轉速即可實現對四旋翼飛行姿態的控制。為使得四旋翼能夠按照設計的姿態與軌跡進行飛行，必須首先對四旋翼進行建模，然后根據得到的模型設計飛行控制系統并進行仿真驗證。因此，對四旋翼進行建模，在此基礎之上設計合理的控制率，并進行仿真驗證是四旋翼實現各種姿態與路徑飛行的關鍵。目前，四旋翼的控制方法主要有反步控制、H∞控制與滑模控制等（王樹剛.四旋翼直升機控制問題研究[D].哈爾濱:哈爾濱工業大學,2006;聶博文.微小型四旋翼無人直升機建模及控制方法研究[D].長沙:國防科學技術大學,2006;王麗新.基于滑模理論的四旋翼直升機的姿態控制研究[D].沈陽:東北大學,2009）。

本文對通過對四旋翼進行動力學分析，建立了四旋翼的動力學模型，并對其進行了化簡。根據化簡的模型，使用PID控制方法設計了四旋翼飛行控制率，并在Matlab/Simulink中對其進行了仿真驗證。

本文共分為四個部分，第一部分對四旋翼與本文目的進行了簡述，第二部分簡要介紹了四旋翼動力學建模與簡化的內容，第三部分完成了對四旋翼模型的仿真、PID控制率設計與驗證，第四部分對全文進行了總結，并提出了未來工作的重點方向。

2.四旋翼動力學建模與簡化

2.1 基本假設與坐標系變換

正常情況下，四旋翼飛行器結構呈X型。

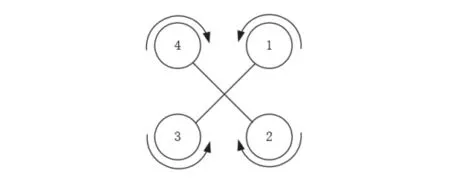
圖2 四旋翼飛行器結構

在為四旋翼建模之前，為簡化模型分析，抓住主要矛盾，忽略次要矛盾，提出以下七點假設：

（1）四旋翼飛行器是剛體，在其飛行過程中質量保持不變；

（2）地面坐標系視為慣性坐標系；

（3）地球表面是平的，且忽略地球自轉與公轉；

（4）重力不隨高度變化而變化；

（5）四旋翼飛行器形狀與質量是關于中心對稱的（吳森堂,費玉華.飛行控制系統[M].北京:北京航空航天大學出版社,2005:46-47）；

（6）四旋翼低速飛行時忽略空氣摩擦力；

（7）四旋翼進行低速小角度飛行。

首先為四旋翼建立合適的坐標系。

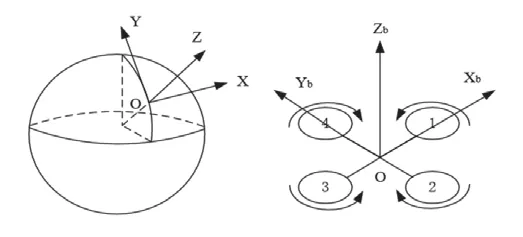
圖3 地面坐標系與機體坐標系

其中，地面坐標系定義如下：選取地面上的一點，即四旋翼至地球中心連線與地面的交點，定義X軸指向水平正東方向，Y軸指向水平正北方向，Z軸垂直于XOY平面，指向天空，即與重力方向相反。

機體坐標系定義如下：由于四旋翼在形狀上關于中心對稱，因此四條機臂是等價的。選取Xb軸指向其中一條機臂的方向，Yb軸指向逆時針轉過90°，與Xb軸垂直的另一條機臂的方向，Zb軸垂直于XOY平面，指向四旋翼飛行器上方。

為確定四旋翼姿態，分別定義歐拉角如下。

●滾轉角φ：在YOZ平面的投影與OY的夾角

●俯仰角θ：在XOZ平面的投影與OZ的夾角

●偏航角ψ：在XOY 平面的投影與OX的夾角

從機體坐標系變換至地面坐標系的轉換矩陣記作Rg/b，需要經過三次歐拉旋轉獲得（許喆.四旋翼無人機控制系統的設計與實現[D].南京:南京理工大學,2017）：

首先，繞Zb轉動ψ角，變換至中間坐標系A，此變換矩陣記作RA/b。

之后，繞轉動θ角，變換至中間坐標系B，此變換矩陣記作RB/A。

最后，繞轉動φ角，變換至地面坐標系，此變換矩陣記作Rg/B。

可得由機體坐標系變換至地面坐標系的轉換矩陣Rg/b。

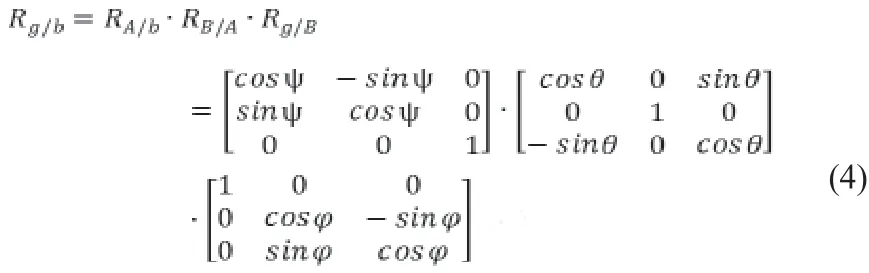
最終得到Rg/b。

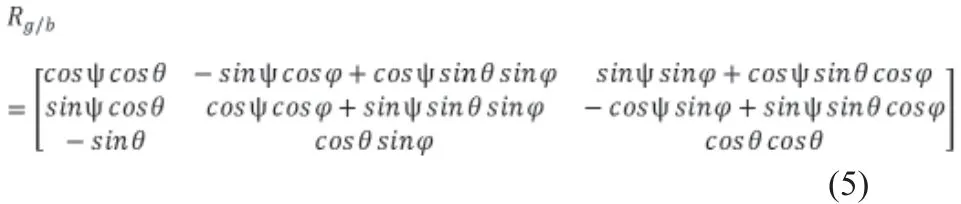
2.2 四旋翼動力學建模

記四個旋翼的轉速分別為～，這也是實際的輸入的控制量。單個旋翼沿軸正方向的拉力可近似認為與該旋翼轉速的平方成正比（米培良.四旋翼飛行器控制與實現[D].大連:大連理工大學,2015）。

其中，f 為升力系數。

容易寫出四旋翼在地面坐標系下受到的合力。

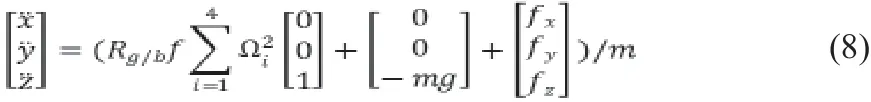
同理，可以寫出機體坐標系下三個力矩平衡方程（馮培晏.四旋翼無人機建模與PID控制器設計[J].工業設計,2018(6):135-137）。

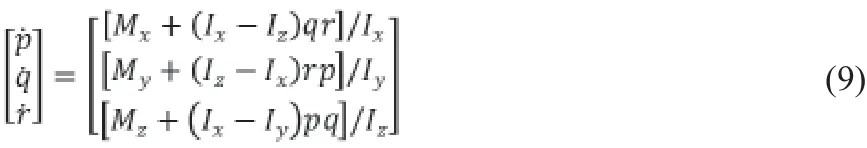
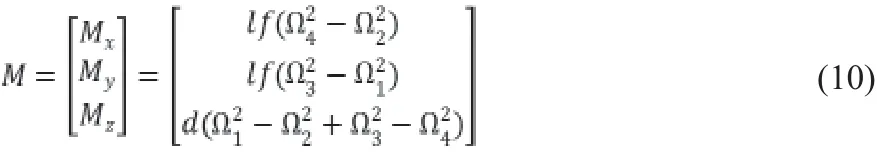
其中，l為四旋翼機臂長，d為電機反扭矩系數。

可以寫出機體坐標系下各軸角速度與四旋翼滾轉、俯仰、偏航角速度之間的關系。

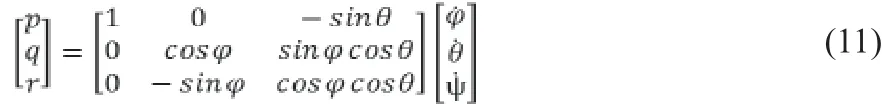
根據前文假設，本文研究的情況為四旋翼無人機小角度、低速度飛行，因此可以做如下近似。

即：

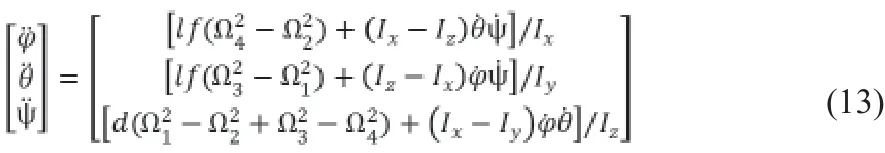
通過對進行變換，令：

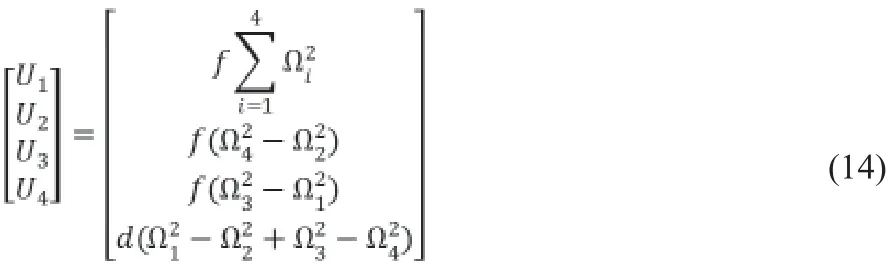
可得四旋翼飛行器最終模型。

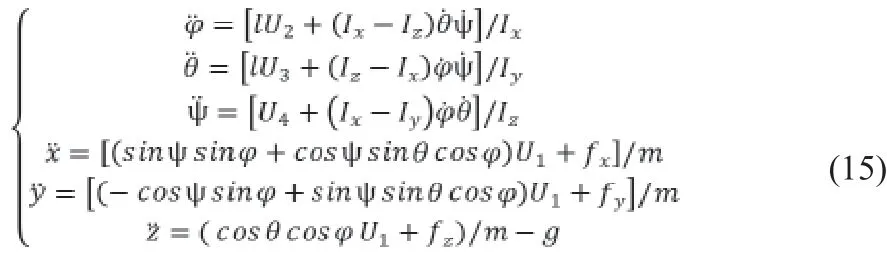
3.四旋翼仿真與控制率設計

3.1 四旋翼模型仿真

根據查閱的文獻（李俊,李運堂.四旋翼飛行器的動力學建模及PID控制[J].遼寧工程技術大學學報(自然科學版),2012,31(1):114-117），得到四旋翼模型參數如表1所示。

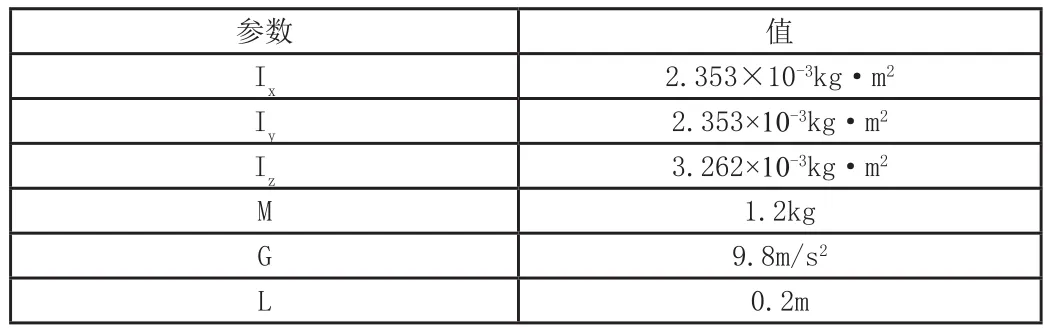
表1 四旋翼模型參數

四旋翼仿真使用Matlab/Simulink完成。仿真模型代碼如下：

其中，使用rand()函數，生成0～1之間的隨機數，以模擬四旋翼受到的擾動。

3.2 四旋翼控制率設計

由四旋翼模型可以看出，其模型有四個輸入變量與六個輸出變量，屬于不完全控制，各變量之間相互之間存在耦合。

在設計控制率時，首先對模型進行化簡。由于本文假設四旋翼是在小角度、低速度的情況下進行飛行，因此可以忽略陀螺效應對三軸角速度帶來的影響（米培良.四旋翼飛行器控制與實現[D].大連:大連理工大學,2015）。從而得到化簡后的模型。

觀察化簡后的四旋翼模型，可以發現其三個姿態角變量以及高度變量僅與四個輸入變量有關，而X、Y軸位置的控制則同時與輸入以及姿態角有關（米培良.四旋翼飛行器控制與實現[D].大連:大連理工大學,2015）。四旋翼飛行器的姿態與高度均完全可控。因此，將四旋翼模型拆分成兩個子控制系統，內環系統為姿態控制系統，外環系統為位置控制系統。

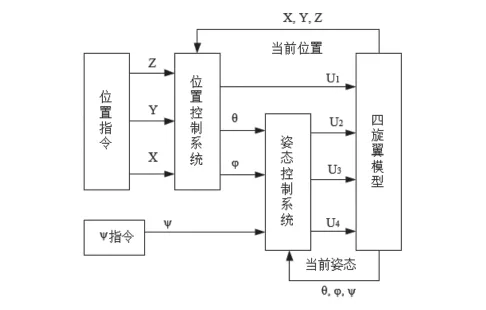
圖4 姿態角控制系統與位置控制系統

系統使用PID控制率進行控制。PID是P（比例）算法與I（積分）算法與D（微分）算法三種算法各種組合的統稱。可以選擇為PD，PI，單獨的P算法等。P（比例）以減少系統穩定性為前提減小系統誤差。I（積分）和D（微分）必須和P（比例）控制搭配使用，I（積分）反映系統的累計偏差，使系統消除穩態誤差。D（微分）反映系統偏差信號的變化率，具有預見性，從而進行超前控制（馮培晏.四旋翼無人機建模與PID控制器設計[J].工業設計,2018(6):135-137）。

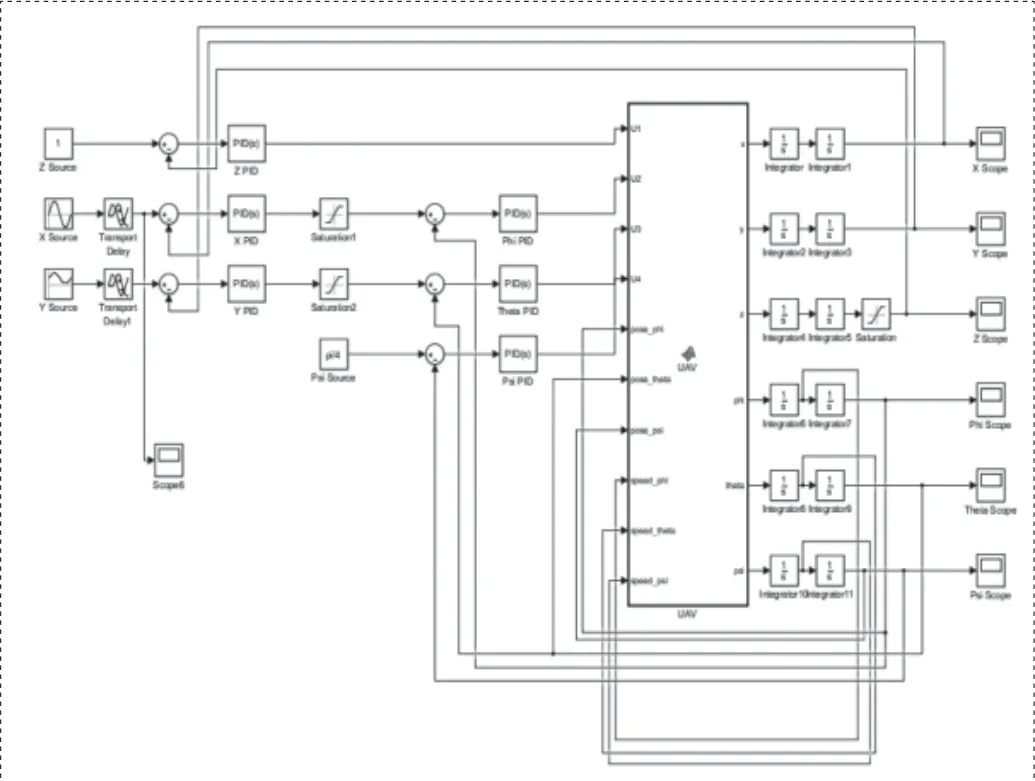
圖5 四旋翼控制系統仿真

從系統仿真框圖中可以明顯看出位置與姿態兩個相對獨立的字系統。X、Y位置指令首先輸入外環控制系統，即位置控制系統，其輸出作為內環控制系統，即姿態控制系統的輸入控制四旋翼的滾轉角與俯仰角。采用先調節內環，后調節外環的策略，調節系統各個PID的參數。最終結果如表2所示。

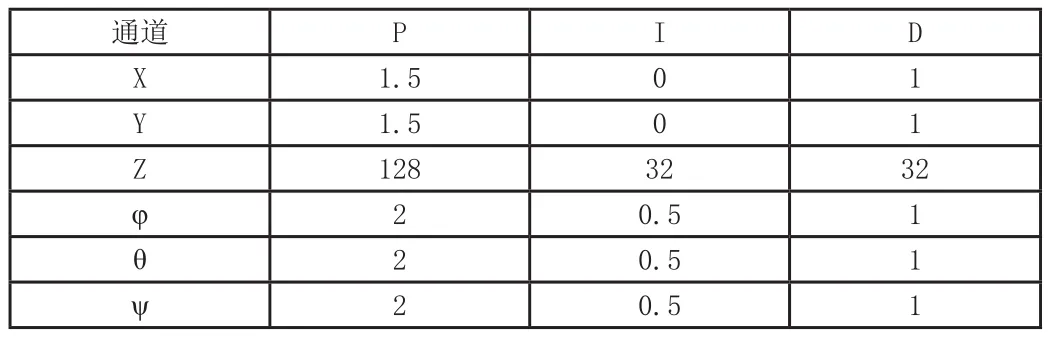
表2 四旋翼PID控制參數

3.3 四旋翼控制率驗證

對控制系統進行測試，令四旋翼在1米的高度按照半徑為2的圓軌跡進行飛行，輸入如下控制指令。

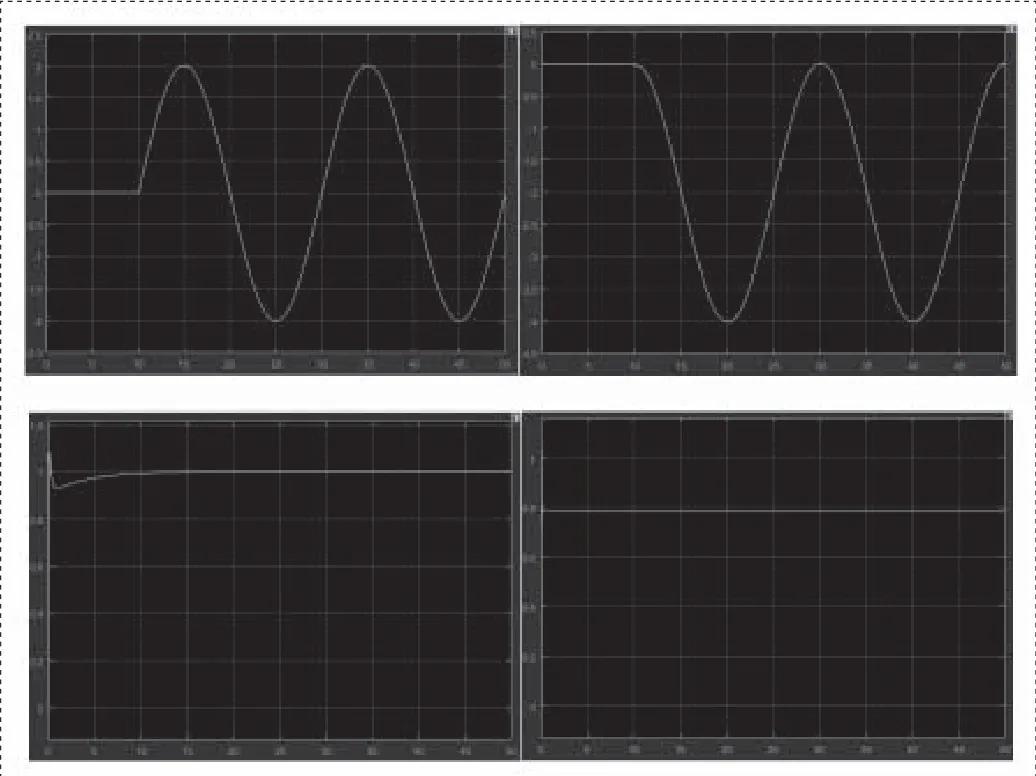
圖7 X、Y、Z與φ控制結果仿真

從結果可以看出，PID控制系統對于四旋翼飛行器有較好的控制效果，飛行器可以在具有擾動的情況下，根據指令按照設計的軌跡進行飛行。

4.結語

本文首先對四旋翼飛行器進行了簡介，之后對四旋翼進行了建模，并對模型進行了簡化，得到了適合控制使用的四旋翼動力學模型。根據得到的模型，本文對該模型進行了仿真，并設計了PID控制率，使得飛行器能夠按照指令沿一定軌跡進行飛行，并驗證了控制率的正確性。

然而，本文的模型與控制率設計仍然存在不足。對比真實的四旋翼模型，本文的模型過于簡單，并沒有考慮到許多實際中可能出現的影響因素，如空氣阻力等。同時，本文的PID控制率也不適用于在復雜的實際條件下進行飛行。未來的工作將會重點集中于對四旋翼進行精確建模，并采取更加先進的控制方法以實現對四旋翼飛行更好的控制效果。