基于模型組合法的我國能源消費需求趨勢預測
王 翀
(1.中國礦業大學管理學院,江蘇 徐州221000;2.淮北師范大學 數學科學學院,安徽 淮北 235000)
0 引言
我國是能源消費大國,隨著工業化和城市化不斷推進,能源消費需求也不斷提高。而與日俱增的能源消費需求,不僅影響我國能源自身安全,而且會對全球能源生產與供給產生一定影響。因此,走綠色低碳的可持續發展道路,不斷減少對能源的依賴,是未來經濟社會發展所必須遵循的規律。對未來能源消費需求趨勢進行把握,對我國能源戰略的制定實施以及保障經濟社會持續發展都具有重要意義。
本文嘗試采用三種單一預測方法得到的預測精度存在較大差異,從側面驗證了組合預測的必要性;在采用協整分析預測時,根據我國經濟情況分別設定了三個GDP增速進行預測,使預測結果更加精確;通過一定模型方法對三種單一預測模型賦予權重,使最終預測結果充分體現單一預測結果包含的信息。
1 樣本數據說明
根據本文的研究需要,共涉及到兩個變量,分別為能源消費總量和地區生產總值,兩個指標分別記為EC和GDP。考慮到數據獲得性,本文選取的時間序列跨度為2000—2016年,數據來源于歷年的《中國統計年鑒》。
根據表1的數據樣本,可得到我國能源消費需求的現狀變化趨勢。
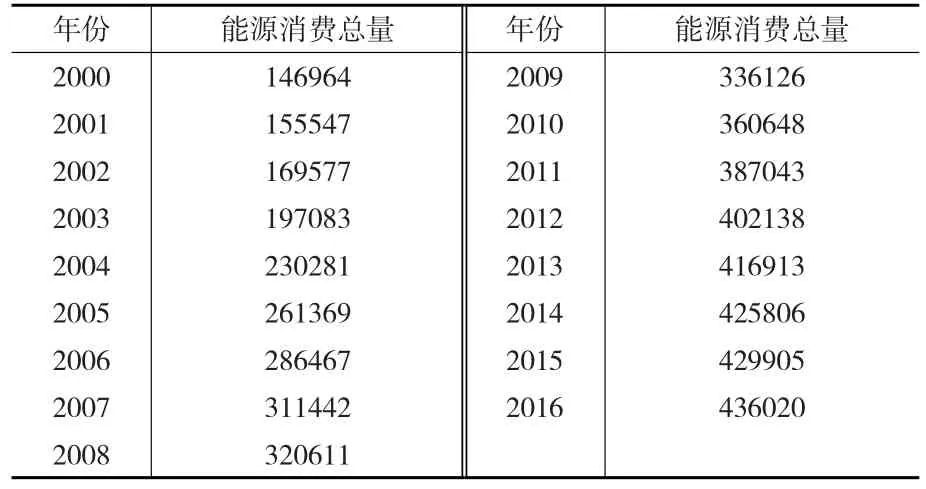
表1 2000—2016年我國能源消費量一覽表 (萬噸標準煤)
2 三種傳統預測方法對我國能源消費需求預測
主要采用協整分析、灰色關聯分析、指數平滑法三種方法,分別對我國能源消費需求趨勢進行初步預測。
2.1 基于協整分析的我國能源消費需求預測
為了通過協整分析方法對我國能源消費需求趨勢進行預測,選擇能源消費總量和地區生產總值兩個指標,通過構建協整方程模型進行計量分析。首先需要對能源消費總量和地區生產總值兩個指標序列進行平穩性檢驗。為了增強序列平穩性,對能源消費總量和地區生產總值均做對數處理,處理后的指標分別記為LnEC和LnGDP。根據單位根檢驗法,得到兩個指標的平穩性檢驗結果,如表2所示。
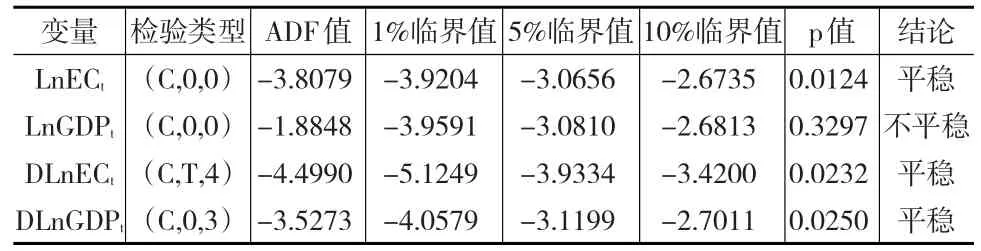
表2 LnEC和LnGDP的單位根檢驗結果
由表2可以看出,LnEC和LnGDP兩個變量均在一階差分后通過ADF顯著性檢驗,即滿足一階單整。根據平穩性檢驗結果,LnEC和LnGDP滿足了協整分析的前置條件。構建LnEC和LnGDP之間的協整關系計量模型如下:

其中,α和β均為待估計參數,εt為模型的隨機誤差項,下標t為年份。
采用Eviews軟件,采用線性回歸方法對式(1)進行估計,結果如下:
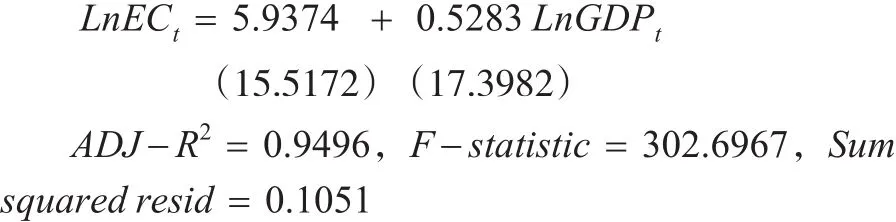
對得到的殘差序列采用單位根檢驗,結果如表3所示。

表3 殘差項的單位根檢驗結果
根據協整分析得到的模型回歸結果,擬合得到2001—2016年歷年的能源消費量的估計值,結果如表4所示。
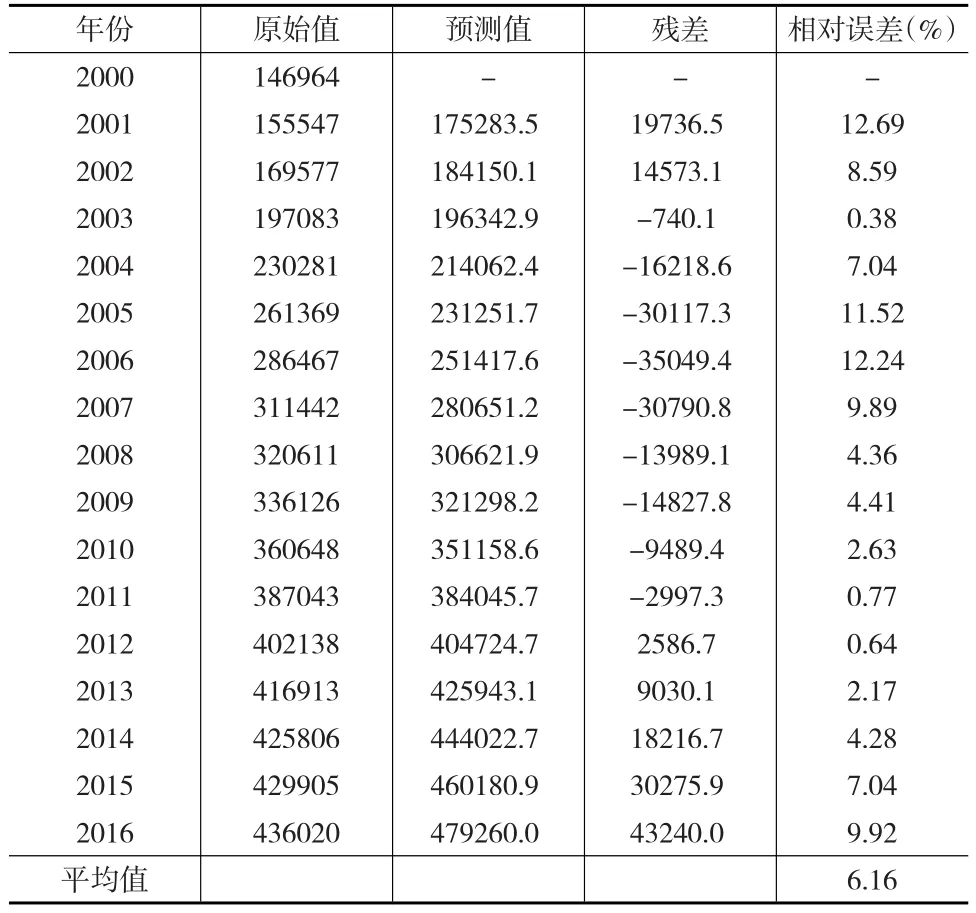
表4 基于協整分析的能源消費需求預測結果(萬噸標準煤)
我國“十三五”規劃中對地區生產總值提出了6.5%的增速,而且國家提出了6.5%應作為經濟增長的底線。2016年,我國地區生產總值的同比增速為6.7%,2017年上半年同比增速達到6.9%,均高于6.5%的增速底線。按照變化趨勢和業界相關專家預測,這里對2017—2025年地區生產總值年均增速分別按照6.5%、6.8%和7%進行預測,結果見表5所示。
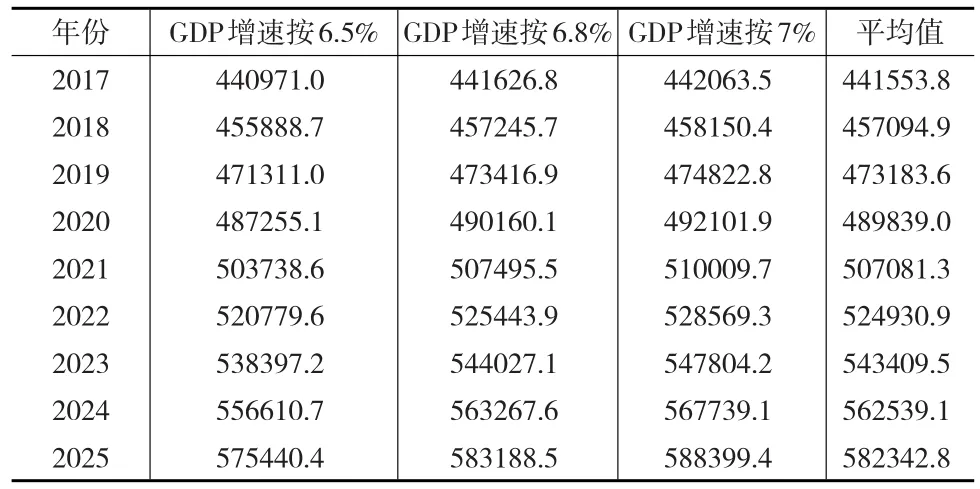
表5 2017—2025年能源消費需求趨勢預測(萬噸標準煤)
2.2 基于灰色關聯分析的我國能源消費需求預測
灰色關聯分析是一種現實的、動態的分析預測方法,具體的步驟如下:
對于給定原始序列x0=(x0(1),x0(2),…,x0(n)),可從原始序列中選擇不同長度的連續數據作為子序列。
于是可生成序列x1(k)=x2(1)+x0(2)+…… +x0(k),(k=1,2,…,n)。
構造如下矩陣B和向量Yn:
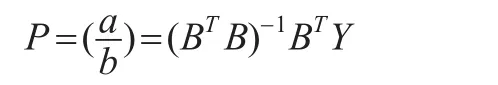
根據得到的系數a,b,可構建GM(1,1)模型如下:
x(1k+1)=(x(01)-b/a)e-ak+b/a
x(0k+1)=x(1k+1)-x(1k)
求解灰色預測模型GM(1,1)可得到預測結果。
運用上述模型,可得能源需求的灰色預測模型為:
x(1k+1)=3991116e0.0585k-3856127
經測算,得到模型預測及誤差情況如表6(見下頁)所示。
計算殘差均方差與原始值均方差的方差比C,可得:
C=10833.1/95478.8=0.1135,平均相對誤差絕對值為3.18%。由此可知,計算的能源消費預測的GM(1,1)模型擬合度較好,對能源消費預測具有一定的參考價值。
2.3 基于指數平滑法的我國能源消費需求預測
指數平滑法,是根據預測對象的歷史數據,通過一定的加權平均進行數據擬合。從2000年以來我國能源消費總量的變化趨勢可以看出,我國能源消費需求呈現一定的線性趨勢,因此,本文采用二次指數平滑法對我國能源消費需求趨勢進行預測。二次指數平滑法的計算模型如下:
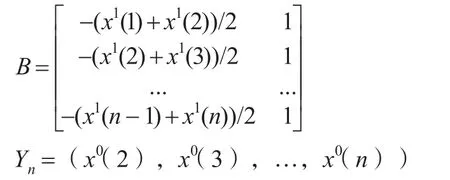
于是,可由最小二乘估計得到系數a和b:
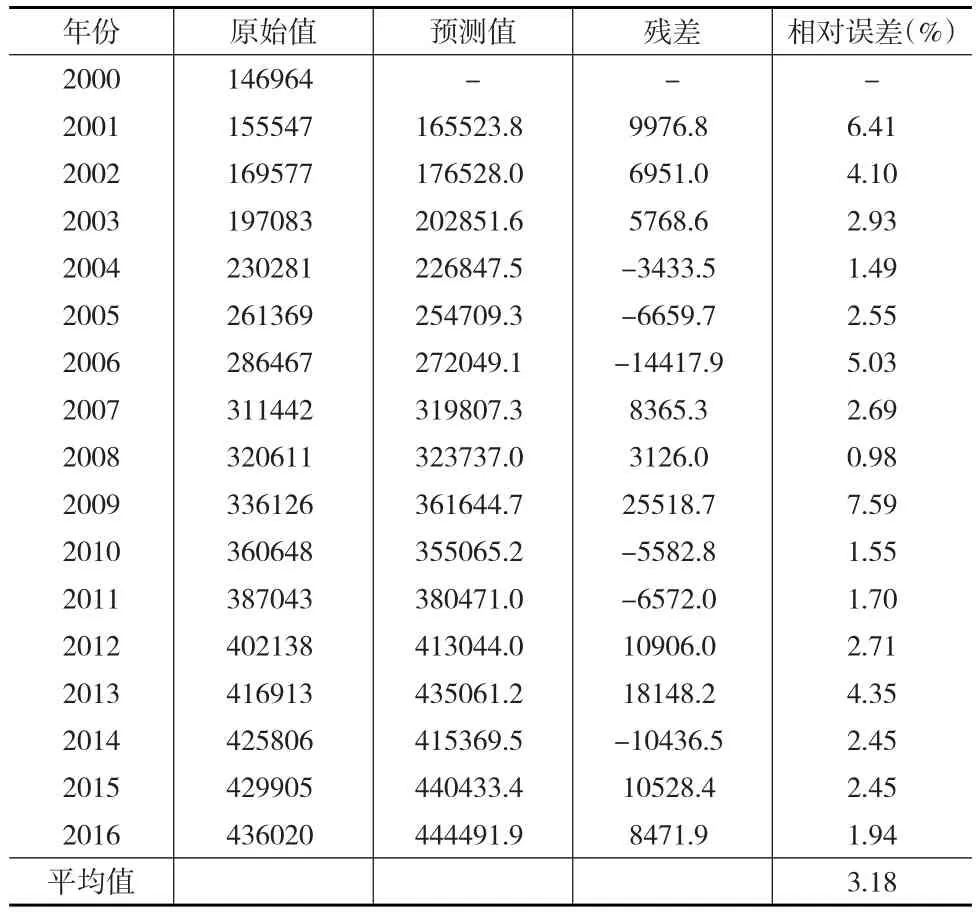
表6 基于灰色關聯分析的能源消費需求預測結果(萬噸標準煤)
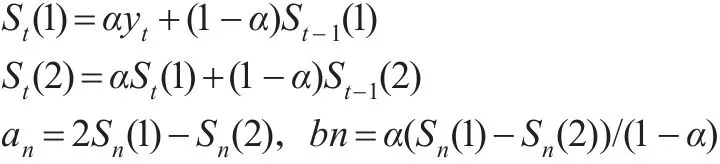
其中,Sn(1)為一次平滑值,Sn(2)為二次平滑值,α為平滑常數經過反復測算比較,發現α取0.3時最優。這里取初始平滑值為原始值前三年的平均值。
經測算,得到模型預測及誤差情況如表7所示。
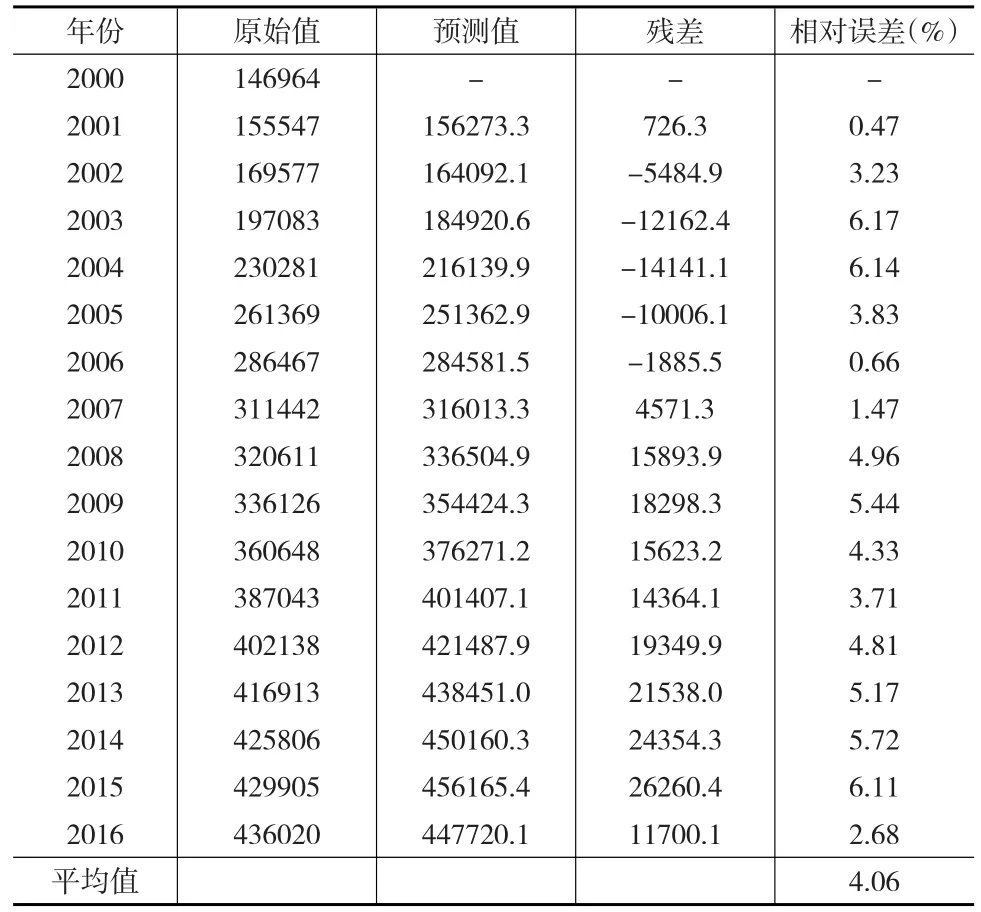
表7 基于指數平滑法的能源消費需求預測結果(萬噸標準煤)
由指數平滑法預測結果可以發現,平均相對誤差絕對值為4.06%,擬合效果也較好,但精度相比灰色關聯法較弱。
3 基于Shapley方法的我國能源消費需求組合預測
3.1 Shapley方法基本思路
設存在n種預測方法,集合為I={1,2,…,n},對其中任意子集s,t,E(s)、E(t)分別為各自組合的誤差。設yi為第i種預測方法最終分配誤差,對于n種方法組合預測帶來的總誤差E(n),會在這n種單項預測中完全分攤,即有:
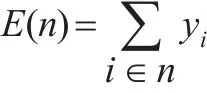
又設i種方法相對誤差的均值為Ei,組合預測法的總誤差為E,則:
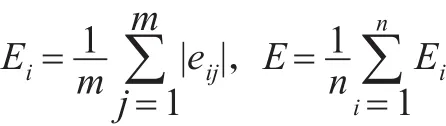
Shapley方法賦權法則為:
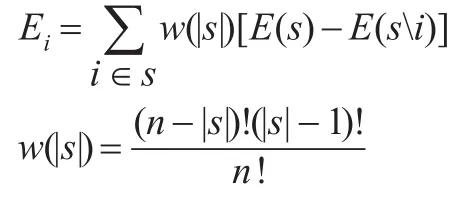
其中,w為單個預測方法i的邊際貢獻,(si)為組合中除去i,Ei為i種方法分攤誤差,|s|為組合中單一預測方法的個數。
第i種預測方法的權重計算如下:
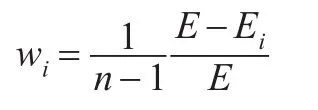
3.2 基于Shapley方法的我國能源消費需求預測
根據前面三種預測方法,可求得組合預測的總誤差值為(6.16+3.18+4.06)/3=4.467。按照Shapley方法,參與組合預測的成員集合為I={1,2,3},其中任意子集的誤差即包含元素的誤差的平均值。于是,得到誤差分攤結果如表8所示。

表8 誤差分攤結果
按照Shapley方法計算模型,可求得各個成員的Shapley值:
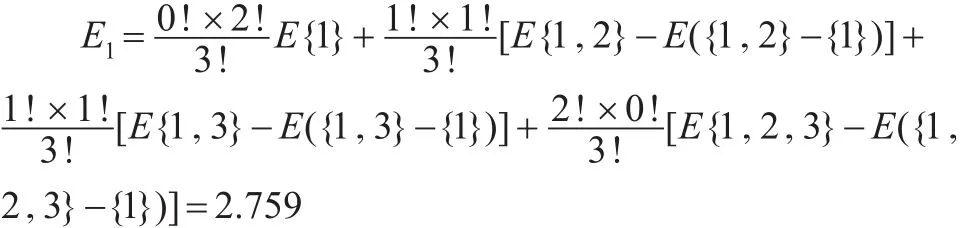
同理,可解得E2=0.671,E3=1.184。于是,三個成員的總分攤值為4.613,加權平均計算,得到各個參與的預測方法的權重分別為0.598,0.145,0.257。因此,可得到組合預測模型如下:
y’t=0.598y’1t+0.145y’2t+0.257y’3t
結合全面三種方法得到的擬合值,可以綜合求得Shapley方法組合預測值,結果如下頁表9所示。
3.3 模型比較及未來趨勢預測
比較表4、表6、表7和表9可以發現,采用Shapley組合預測方法得到的2001—2016年能源消費需求預測結果的平均相對誤差3.05%為最小。因此,可以認為采用Shapley組合預測方法得到的預測結果具有較高的精度,是相對最為有效的。
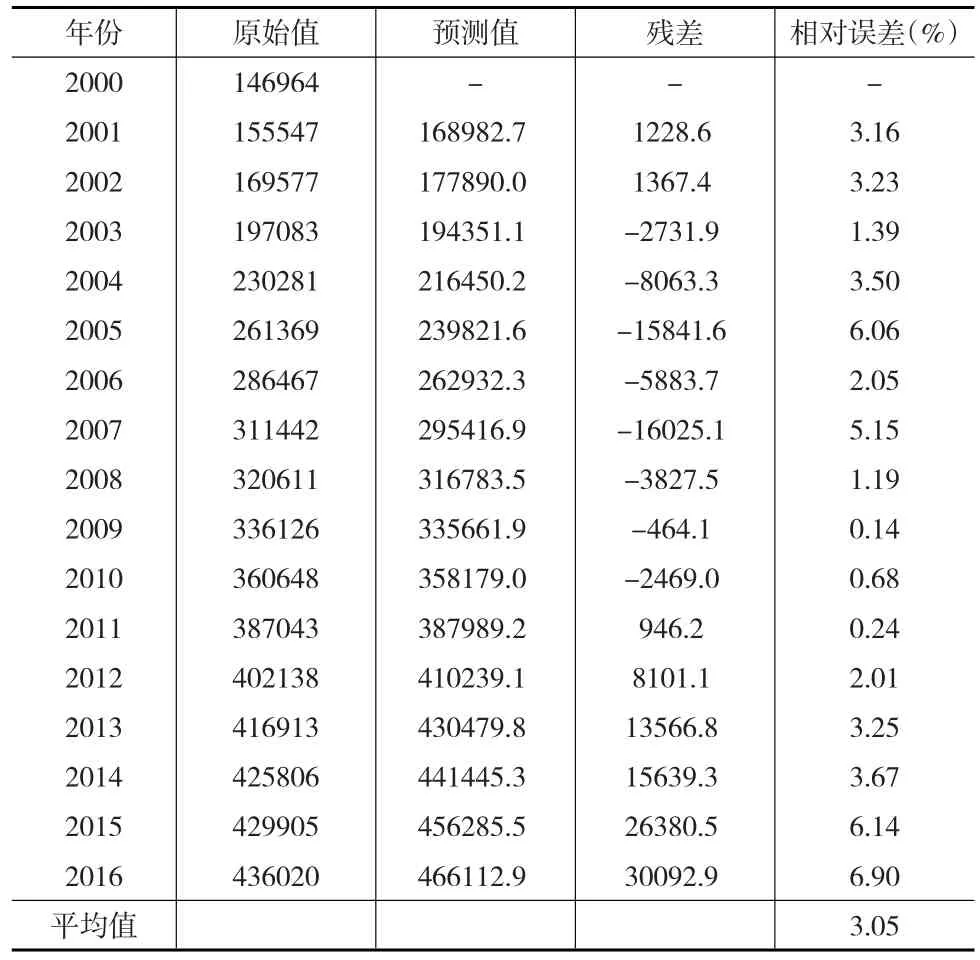
表9 基于Shapley組合預測法的能源消費需求預測結果(萬噸標準煤)
為了對2017—2025年我國能源消費需求趨勢進行綜合預測,根據組合預測模型,首先采用前面三種單一的預測方法進行分年度預測,再根據各個預測方法的權重值進行加權平均,最終得到綜合預測值。結果如表10所示。
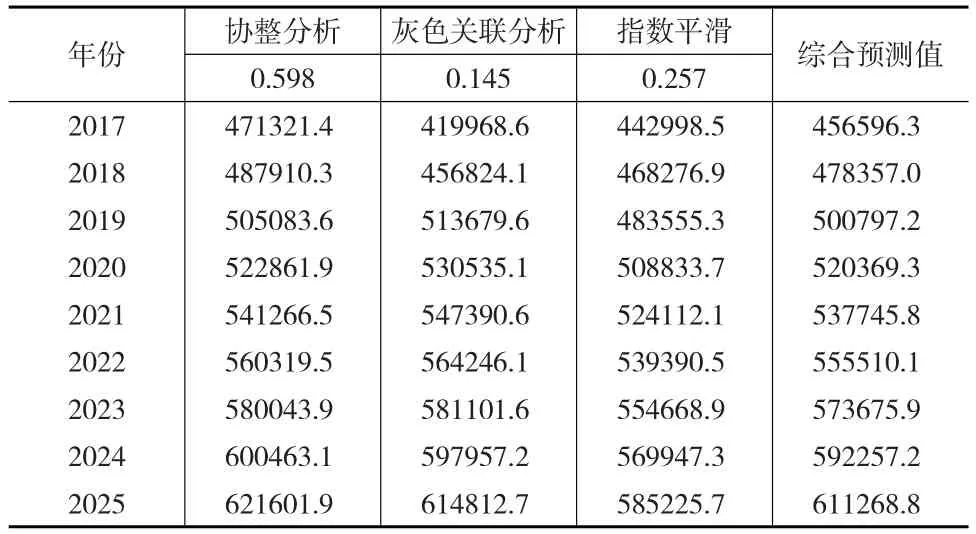
表10 2017—2025年能源消費需求綜合預測結果(萬噸標準煤)
根據表10結果,繪制2017—2025年能源消費需求的變化趨勢圖(圖1)。由圖1可知,未來幾年我國能源消費需求將持續增長,但增速在經歷了未來5年的有所上升之后,在2021—2025年逐步趨于放緩。到2025年,預計能源消費需求量達到57.3億噸標準煤左右,同比增速在3%左右。
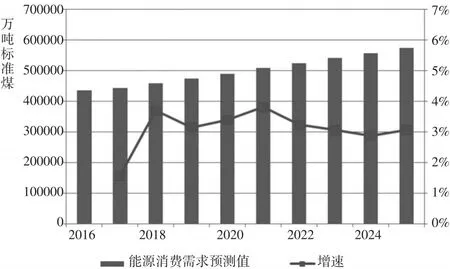
圖1 2017—2025年我國能源消費需求趨勢預測
4 結論
本文在三種單一預測方法的基礎上,構建了一種賦權的組合預測模型,對我國能源消費需求進行預測。組合預測模型充分考慮了不同單一預測模型的優勢。通過不同預測方法比較可知,本文的組合預測模型具有相對較高的精度,因此本文也為能源消費需求預測以及理論預測方法的改進提供了一種新的思路。根據最終預測結果,到2025年我國能源消費增長總體趨緩,增速不斷趨于3%。但是,本文的組合預測模型是基于三類不同預測模型,而對于這些單一預測模型的選擇仍然是一門重要學問。如何通過進一步優化梳理各種預測模型的優勢,通過構建更為精確的組合模型進行預測,將是今后要努力的方向。

