Gompertz曲線參數估計的一種加權方法

王增輝，趙彥軍，姜淑珍，黃東巖

（1.東北師范大學 人文學院，長春 130117;2.吉林大學 工程仿生教育部重點實驗室，長春 130025）

0 引言

Gompertz曲線是一種生長曲線，已廣泛用于描述動物的生長規律和植物中某些物質（例如大豆中的蛋白質以及脂肪）的增長規律。在人口學和經濟領域的研究中也有廣泛的應用。Gompertz曲線是英國統計學家和數學家Gompertz通過大量觀察和研究提出來的。它的一般表達式為：

其中a＞0，b＞0，k＞0。

關于Gompertz曲線中的參數a，b，k的估計。目前的估計方法是先用三點法或四點法來估計參數a，而參數b與k的估計則是將式（1）取對數然后化為曲線模型。最后用普通最小二乘法來估計。本文給了一種估計Gompertz曲線參數估計的加權最小二乘法。通過實例分析可知，本方法相對于不加權的最小二乘法估計法得到的Gompertz曲線擬合效果有明顯的提升。

1 Gompertz曲線參數估計的普通最小二乘法

1.1 Gompertz曲線參數a估計的三點法、四點法

將式（1）變形為：

設給定一組數據 （ti，yi）（i=1，2，…，n）。這里假設xi為等距。即設xi+1-xi=h（i=1，2，…，n-1），h為常數。若n為奇數，取三個點，并帶入式（2）中可解出：

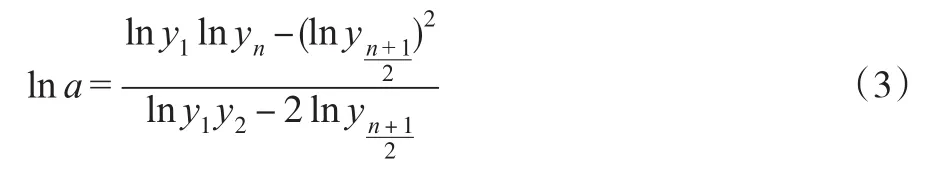
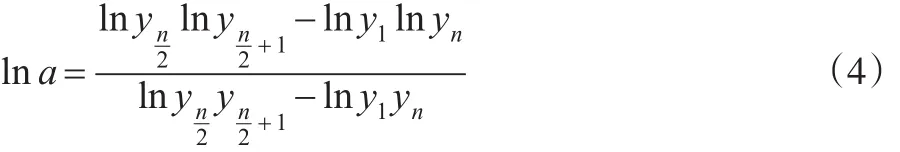
則由式（3）或式（4）可估計出Gompertz曲線中的參數a。

1.2 Gompertz曲線參數b與k的最小二乘估計

對式（2）兩端取自然對數得：

式中的參數A與B可用最小二乘法來估計，其估計公式為：

其中：

t_=于是可估計出Gompertz曲線中的參數

2 Gompertz曲線參數估計的加權法

上面估計Gompertz曲線中參數b與k時，是將式（1）兩端兩次取對數化為線性模型（6）來估計的，由于做了變換，可能破壞等方差的假定，因此應用普通最小二乘法估計式（6）中的參數A與B（從而估計出非線性模型（1）中的參數b與k），可能不理想。對此本文給出了一種估計參數b與k的加權最小二乘法，下面介紹這種加權最小二乘法，這是式（1）中的參數用三點法或四點法來估計。

由多元函數極值原理有：

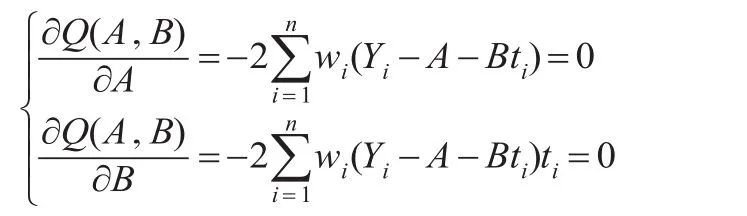
解此方程組可得A與B的加權最小二乘估計為：

顯然若取wi相等，則式（8）就是式（7），因此式（7）是式（8）特例。

對于權wi的選取有多種方式，由于權wi與模型（1）化為線性模型時所做的變換Y=f（y）有關。即權wi與成正比。由于可以取權：

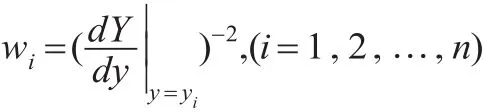
由此可取權：

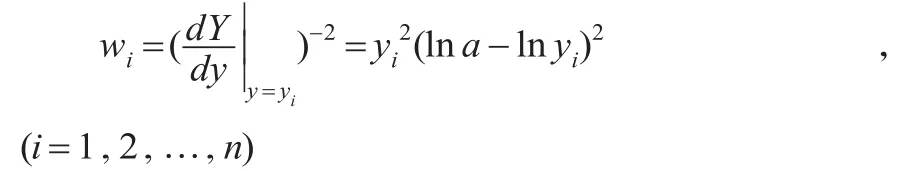
在實際計算時，可將式（8）寫成如下公式：

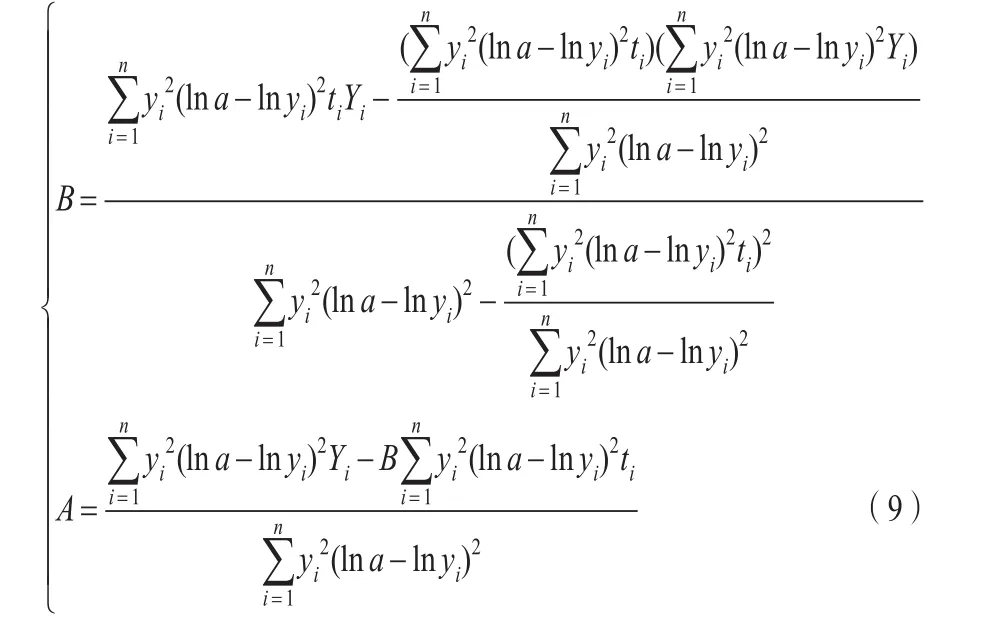
對給定一組數據 （ti，yi）（i=1，2，…，n），將數據代入式（9）中可估計出式（1）中的參數b=eA，k=-B。

3 Gompertz曲線擬合精度的度量

關于曲線擬合的精度的度量，通常選用相關指數R2和殘差平方和Se來度量。

相關指數R2定義為：

殘差平方和定義為：

顯然殘差平方和Se越小,說明曲線擬合越好，而相關指數R2越接近于1，說明曲線擬合的越好。

4 實例

下面通過實例介紹Gompertz曲線參數的加權方法，并給出用普通方法求出的Gompertz模型與本文方法給出的模型進行精度比較。

4.1 實例一

首先探討大豆的葉面積隨時間增長的規律問題。數據如表1所示、

由于共有10個數據，即n=10,因此可用四點法來估計Gompertz曲線中的參數a，選用四個數據，y1=0.4，y5=3.0，y6=3.6，y10=4.8，代入公式（4）中可估計出=4.8624，再將表1中的數據yi進行變換：

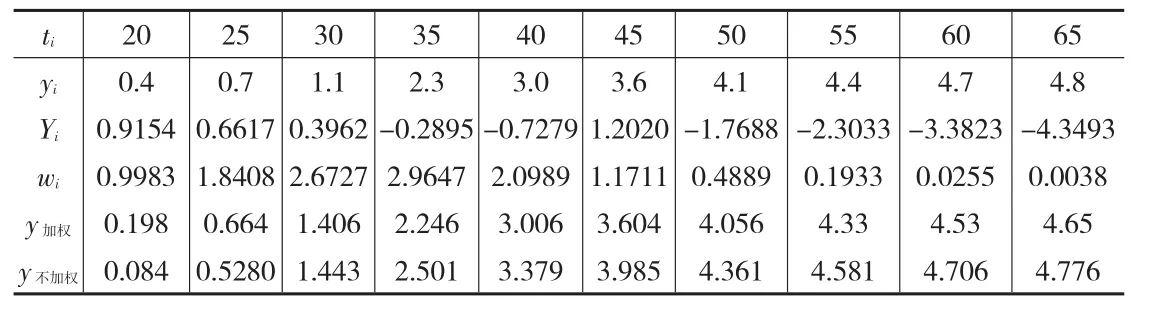
表1 大豆的葉面積指數y（t）與生長日數t之間的關系

并列入表1中，并求出權wi列入表1中，同時可計算出：

由公式（8）可估計出：

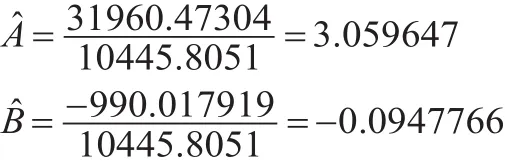
于是可估計出Gompertz曲線參數的加權估計為=eA?=21.32003，k?=-B?=0.0948，因此得描述大豆面積的Gompertz曲線為：

為了比較加權參數估計方法與不加權參數估計方法所得的Gompertz曲線的擬合精度，本文求出不加權的Gompertz曲線模型：

由表1中的數據可求出：

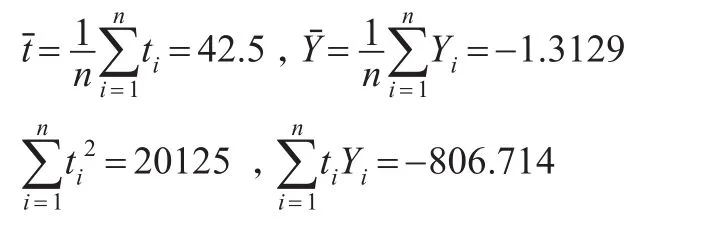
由公式（7）可估計出：

于是求出b與k的估計值分別為：

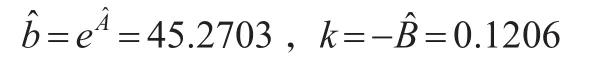
由此得到描述大豆面積生長規律的不加權Gompertz曲線模型為：

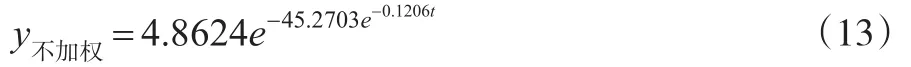
現在比較一下參數加權估計與不加權參數估計得到Gompertz模型（12）與（13）的擬合精度，用模型（12）與（13）分別計算出在各ti處的預測值分別列入表1中，再由公式（10）與（11）求出：

由此可看出加權參數估計方法的擬合精度比不加權參數估計方法的擬合精度有明顯提高，若從殘差平方和的角度看，加權方法的誤差是不加權的誤差的三分之一。

4.2 實例二

某地區1993—2010年某種家電銷售量分析，數據來源于《中國統計年鑒》,具體數據如表2所示。

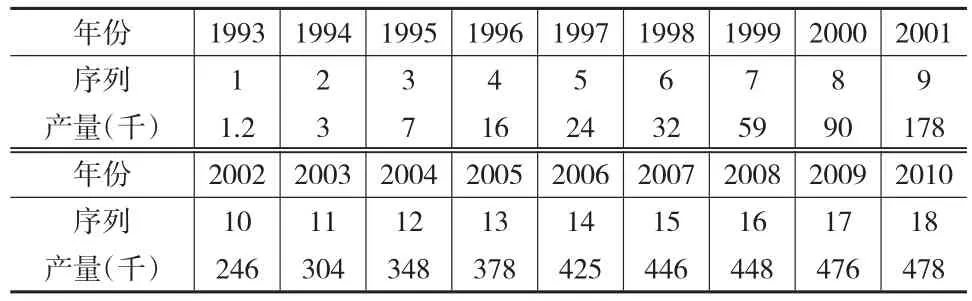
表2 家電銷售量（千臺）y（t）與年份t之間的關系

家電銷售量隨時間增長規律和趨勢比較符合用Gompertz曲線模型來擬合。由于數據總數為18為偶數，首先用公式（4）來估計模型中的參數a，因此選用四個數據y1=1.2，y9=178，y10=246，y18=478代入公式（4）中可求a的估計值為a=500.6 ，然后將已知數據tilna=ln500.6，yi，代入公式（9）中可求出A加權=3.0137，B加權=-0.3332，于是可估計出b加權=eA加權=20.3629，k加權=-B加權=0.3332。從而得到描述家電銷售規律的Gompertz曲線模型為：

下面再用普通最小二乘法求出描述家電銷售規律的Gompertz曲線模型。

由于參數a已由前面估出。只需估計參數b與k,將數據代入式（7）中可估計出A不加權=3.0027，B不加權=-0.3002 ，得到不加權k不加權=-B不加權=0.3002。于是求出不加權情況下描述家電銷售規律的Gompertz曲線模型為：

現在對兩種不同方法得到的Gompertz曲線的擬合精度進行比較。由公式（10）與（11）可計算出兩個模型的殘差平方和與相關指數分別為：

由此可以看出加權參數估計方法的精度在顯著提高，從殘差平方和可知不加權的殘差平方和是加權的殘差平方和的15倍之多。

5 結論

（1）本文給出的Gompertz曲線參數估計的加權方法相比不加權方法，其參數估計的精度都有所提高，特別是當給出的測試數據波動比較大時，精度提高更為明顯。

（2）若在公式中取權wi=w（常數）（i=1，2，…，n），則公式（8）就是公式（7），因此公式（7）是公式（8）的特例。

（3）關于權wi（i=1，2，…，n）的選擇有多種方法，例如可以選擇wi=，也可以選擇wi=，k為常數，由權wi的選取不同，其參數估計的結果也不同。