基于概率模型的非均勻數(shù)據(jù)聚類算法

楊天鵬，陳黎飛,2

(1.福建師范大學(xué) 數(shù)學(xué)與信息學(xué)院，福州 350117; 2.福建師范大學(xué) 數(shù)字福建環(huán)境監(jiān)測物聯(lián)網(wǎng)實驗室，福州 350117)(*通信作者電子郵箱clfei@fjnu.edu.cn)

0 引言

聚類分析作為數(shù)據(jù)挖掘的一種重要方法，目的是將給定數(shù)據(jù)劃分成多個子集(每個子集為一個簇)，使得簇內(nèi)對象彼此相似，與其他簇對象不相似[1]。傳統(tǒng)的聚類算法可分為層次聚類、基于劃分聚類、基于密度和網(wǎng)格聚類，以及其他聚類算法[2-3]。目前聚類分析已廣泛應(yīng)用在Web搜索、圖像處理、模式識別、醫(yī)療數(shù)據(jù)分析等眾多領(lǐng)域。

作為數(shù)據(jù)挖掘十大算法之一，K-means算法[4]因其簡單高效的優(yōu)點得到廣泛的研究和應(yīng)用[5]。然而，受“均勻效應(yīng)(uniform effect)”的影響[6]，K-means型算法在聚類醫(yī)療診斷等復(fù)雜數(shù)據(jù)時性能受限。這類數(shù)據(jù)的一個特點是同一數(shù)據(jù)集同時包含了樣本數(shù)量和樣本密度有較大差異的簇，這種數(shù)據(jù)稱為非均勻數(shù)據(jù)(non-uniform data)。與不平衡數(shù)據(jù)(主要指簇樣本量即簇大小差異較大的數(shù)據(jù))聚類[7]相比，非均勻數(shù)據(jù)聚類問題更具普遍性。例如，在含有“正常”和“患病”兩個簇的疾病診斷數(shù)據(jù)中，兩簇的大小差異明顯(通常，“正常”簇比“患病”簇的樣本數(shù)量大得多)，更重要地，“患病”簇的樣本皆具特定的疾病模式，其密度比“正常”簇有顯著區(qū)別(表現(xiàn)為“正常”簇樣本分布的方差大得多)。

針對該問題研究者提出了多種方法[8-12]，可大致分為三類：第一類方法基于樣本抽樣，在聚類之前首先對樣本集作欠采樣或過采樣的處理操作，文獻[8-9]即是在這樣預(yù)處理后的數(shù)據(jù)上進行K-means聚類的；第二類方法在聚類模型中考慮不同簇的樣本量差異，例如，文獻[10]引入簇的樣本數(shù)量，給出了經(jīng)典模糊聚類算法目標優(yōu)化函數(shù)的兩種改進方案；第三類方法則側(cè)重簇的密度差異，借助多代表點等方法[11]以區(qū)分數(shù)據(jù)集中的不同密度區(qū)域。這些方法是分別針對簇樣本數(shù)量不平衡特性或密度差異特性而提出的，未提供同時處置非均勻數(shù)據(jù)上述兩個特性的解決方案。

從原理上說，K-means型聚類是一種基于模型的方法，它所學(xué)習(xí)的概率模型是以相關(guān)參數(shù)為常數(shù)這一假設(shè)前提下的一種簡化的高斯混合模型[13]，此簡化模型并不能很好地刻畫非均勻數(shù)據(jù)簇類的兩個特點。為此，本文提出一種基于概率模型的非均勻數(shù)據(jù)聚類新算法——MCN(Model-based Clustering on Non-uniform data)，以應(yīng)對傳統(tǒng)K-means型算法的“均勻效應(yīng)”問題。本文的主要工作包括兩個方面：其一，以高斯混合模型為基礎(chǔ)，建立了非均勻數(shù)據(jù)簇的概率模型，新模型可以描述同一數(shù)據(jù)集中樣本量和密度都存在差異的簇；其二，基于提出的模型推導(dǎo)了聚類目標函數(shù)，并給出優(yōu)化目標函數(shù)的算法步驟，實現(xiàn)了非均勻數(shù)據(jù)的軟子空間聚類。在合成數(shù)據(jù)和實際數(shù)據(jù)上的實驗結(jié)果表明，與現(xiàn)有的非均勻數(shù)據(jù)聚類算法相比，本文MCN算法有效提高了聚類精度。

1 相關(guān)工作

首先給出文中使用的符號及定義。令待聚類數(shù)據(jù)集為DB，含N個D維樣本，任一樣本用x=〈x1,x2,…,xj,…,xD〉表示，其第j(j=1,2,…,D)維屬性為xj。考慮硬聚類算法，它將DB劃分成K個不相交的子集的集合C={c1,c2,…,ck,…,cK}, 并稱子集ck為DB的第k(k=1,2,…,K)個簇，|ck|表示該簇包含的樣本數(shù)量。用vk=〈vk1,vk2,…,vkD〉表示ck的簇中心,V={v1,v2,…,vK}為全體簇中心的集合。

經(jīng)典的K-means算法是一種劃分型聚類算法，其優(yōu)化目標定義為：

(1)

K-means通過類期望最大化(Expectation Maximization, EM)算法[15]的學(xué)習(xí)過程求取式(1)的局部優(yōu)解，過程如下：給定簇數(shù)目K，首先選擇K個初始簇中心，然后計算每個樣本與各簇中心點的距離，將樣本劃分至距離最小的簇，再為每個新劃分生成的簇計算最優(yōu)的簇中心；算法迭代執(zhí)行上述“劃分-簇中心優(yōu)化”步驟，直到滿足停止條件算法終止，得到對應(yīng)式(1)局部優(yōu)解的數(shù)據(jù)集聚類劃分。

圖1 “均勻效應(yīng)”的例子Tab. 1 An example of “uniform effect”

文獻[6]分析了K-means聚類的“均勻效應(yīng)”現(xiàn)象。以聚類圖1(a)中的非均勻數(shù)據(jù)為例。圖1(a)隱含有3個簇Cluster1、Cluster2和Cluster3，它們不但在大小(樣本數(shù))上有差異，簇密度也顯著不同，例如，Cluster1和Cluster2中樣本分布方差顯然有較大差別。該數(shù)據(jù)的K-means聚類結(jié)果如圖1(b)所示，其中樣本數(shù)較少的Cluster2會“吞掉”樣本較多的簇Cluster1的部分樣本，使得兩個簇的大小和密度趨向于相同，此即K-means型算法的“均勻效應(yīng)”。

從統(tǒng)計學(xué)習(xí)[16]的角度，K-means可以看作是一種基于模型的統(tǒng)計聚類算法。這里，視簇ck的每個樣本x源自如下高斯分布：

(2)

那么，給定數(shù)據(jù)集DB，劃分聚類的目標就是搜索最小化下面負對數(shù)似然函數(shù)的模型參數(shù)(C,V)：

(3)

注意到式(3)的推導(dǎo)結(jié)果與K-means算法的優(yōu)化目標是相同的，見式(1)。

上面推導(dǎo)過程基于如下基本假設(shè)：每個簇的樣本方差σ是一個常數(shù)。如前所述，σ體現(xiàn)了簇的密度。這從模型的角度解釋了 “均勻效應(yīng)”產(chǎn)生的一個原因：K-means型算法致力于求解密度相近的簇集合。此外，從式(3)還可以看出，K-means算法的優(yōu)化目標也沒有體現(xiàn)不同簇中樣本數(shù)量的差異，這也是其所假設(shè)的概率模型所決定的：對應(yīng)不同簇的高斯分布分量以一種“平等”的方式進行混合建模。因此，為提高K-means型算法在非均勻數(shù)據(jù)上的聚類性能，下面首先提出一種新的高斯混合模型，以區(qū)分簇類在樣本數(shù)量和密度上的差異；接著，以此為基礎(chǔ)，推導(dǎo)出一種新型的非均勻數(shù)據(jù)聚類算法。

2 非均勻數(shù)據(jù)聚類模型及算法

本章首先建立用于非均勻數(shù)據(jù)聚類的高斯混合模型，然后定義基于模型的聚類目標優(yōu)化函數(shù)，最后給出聚類算法。

2.1 非均勻數(shù)據(jù)聚類模型

如前所述，在一個非均勻數(shù)據(jù)集中，簇的密度通常存在差異。為刻畫這種差異，引入兩組記號：用σk2(k=1,2,…,K)表示簇ck的方差，其值越大，表明ck的密度越小；進一步，引入向量wk=〈wk1,wk2,…,wkj,…,wkD〉，其各元素wkj>0，用于區(qū)分簇ck在不同屬性上的密度差異，值越大表明ck投影在相應(yīng)屬性上時數(shù)據(jù)分布的密度越小。由此，ck屬性j上數(shù)據(jù)分布的方差可用σk2/wkj來表示。將這個方差表達式代入形如式(2)的高斯密度函數(shù)，得到任意樣本x∈ck投影在屬性j上的概率密度函數(shù)，如下：

(4)

在此基礎(chǔ)上，基于數(shù)據(jù)集的D個屬性是統(tǒng)計獨立的這一“樸素”假設(shè)[17]來建立簇的模型。雖然該假設(shè)在一些實際數(shù)據(jù)上并不現(xiàn)實，但它可以有效降低所構(gòu)造模型的復(fù)雜性：簡單地通過一組變量邊緣分布的乘積來估計向量的概率密度。這樣，令P(x)表示ck中任一樣本的概率密度，有:

(5)

接下來，考慮非均勻數(shù)據(jù)的另一個特性：同一數(shù)據(jù)可能包含大小各異的簇。為此，引入代表簇大小的記號αk(k=1, 2,…,K)，滿足約束條件：

(6)

其數(shù)值大小與簇所包含的樣本數(shù)量相關(guān)，可以看作是賦予每個簇的一種權(quán)重。根據(jù)這些定義，非均勻數(shù)據(jù)的加權(quán)似然函數(shù)表示為：

(7)

其中：Θ={(ck,σk,vk,wk)|k=1,2,…,K}為K組參數(shù)的集合。

基于上述模型，給定數(shù)據(jù)集DB和簇數(shù)K，聚類轉(zhuǎn)變成了從DB求取優(yōu)化的參數(shù)Θ以最大化加權(quán)似然的問題：

上式在式(7)基礎(chǔ)上使用了對數(shù)變換，受條件式(6)約束。代入式(4)和(5)，并略去其中的常數(shù)項，優(yōu)化目標改寫為：

(8)

對比式(1)可知：

1)當所有的αk、σk和wkj都為常數(shù)，J2退化為K-means算法的優(yōu)化目標函數(shù)J0。這意味著K-means假定了所有簇具有相同的大小和相同的方差，且各簇每個屬性上的數(shù)據(jù)分布密度也是相同的。而新的目標函數(shù)通過σk、vk和wk等參數(shù)可以區(qū)分簇類這些各異的特性；

2)在J2表達式中，wkj主要作用于xj與vkj間距離(實際上是二者間的平方誤差，數(shù)值上等于二者歐氏距離值的平方)的計算。從效果上看，衡量屬性密度差異的wkj(j=1,2,…,D)相當于賦予各屬性的特征權(quán)重，其數(shù)值大小反映了各屬性對距離度量的貢獻程度。因此，優(yōu)化J2的過程可以看作是對非均勻數(shù)據(jù)集實施的軟子空間聚類[14]。

2.2 軟子空間聚類算法

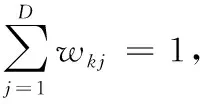
根據(jù)拉格朗日乘子法，將wkj、αk的約束條件引入到目標函數(shù)中，可得帶約束條件的聚類優(yōu)化目標函數(shù)為：

(9)

其中：λk和η為拉格朗日乘子。

上述目標函數(shù)參數(shù)的求解是非線性函數(shù)的優(yōu)化問題，難以求得全局最優(yōu)解。本文MCN算法基于常用的EM算法結(jié)構(gòu)求取其局部最優(yōu)解。為敘述方便，引入符號W={wkj|k=1,2,…,K;j=1,2,…,D}和Λ={α1,α2,…,αK,σ1,σ2,…,σK}。參數(shù)的求解可分為以下幾個步驟：

1)固定W、V、Λ,求C。對任意一個樣本x根據(jù)以下公式進行簇劃分：

(10)

式(10)通過比較樣本x源自各高斯分量的概率將其劃分到概率最大的簇中。

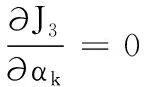
αk=|ck|/N

(11)

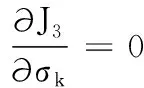
(12)

從式(12)可知，σk2即是第k個簇中樣本分布的加權(quán)散度，反映了非均勻數(shù)據(jù)中各簇有差異的密度信息。根據(jù)以上分析，算法的最優(yōu)解αk和σk2能刻畫非均勻數(shù)據(jù)中不同簇之間樣本數(shù)量和密度都可能存在差異的特點。

(13)

式(13)為簇中心點求解公式，通過該式完成簇中心點的更新。

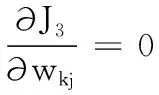
(14)

式(14)通過求解wkj為各特征賦予不同的權(quán)重，效果上相當于將第k個簇的樣本投影到相應(yīng)的子空間中。

根據(jù)上述參數(shù)求解方法，可以得到基于概率模型的非均勻數(shù)據(jù)軟子空間聚類算法如下。

輸入 數(shù)據(jù)集DB，簇數(shù)目K。

輸出 簇劃分C。

初始化 隨機生成初始簇中心vk,并令wkj=1/D,σk=1/K,αk=1/K(k=1,2,…,K;j=1,2,…,D)。

Repeat:

更新C：利用式(10)更新簇劃分；

更新vkj：根據(jù)式(13)，更新vkj；

更新αk、σk：根據(jù)式(11)、(12)更新αk、σk;

計算wkj：先計算λk,并將求得的λk代入到式(14)中求得wkj;

Until:滿足迭代停止條件

根據(jù)上述算法步驟可知本文MCN算法的時間復(fù)雜度為O(PKND)，其中P為算法的迭代次數(shù)。

3 實驗

實驗平臺為：Core i5-3470 3.2 GHz CPU，4 GB內(nèi)存，操作系統(tǒng)為Windows 7。算法采用Java編寫。

3.1 實驗設(shè)置

實驗選擇了GMM[16]、Verify2[19]、IFCM[10]三種算法進行對比。GMM作為基于概率模型的典型聚類算法，將其作為對比算法用來驗證經(jīng)典的概率模型和結(jié)合子空間技術(shù)的概率模型在非均勻數(shù)據(jù)上的表現(xiàn)；Verify2為文獻[19]提出的一種將欠采樣和譜聚類結(jié)合對類不平衡數(shù)據(jù)進行聚類分析的方法，其中欠采樣是非均勻數(shù)據(jù)預(yù)處理方法中的一種代表性方法；IFCM為文獻[10]中提出的基于樣本數(shù)量加權(quán)的模糊聚類算法。

圖2 DS1投影到部分低維空間中的數(shù)據(jù)分布Tab. 2 Distribution of DS1 projected on some low-dimensional spaces

因為非均勻數(shù)據(jù)不同簇之間樣本存在較大差異，合成數(shù)據(jù)能夠從簇的數(shù)目、大小等控制數(shù)據(jù)集的簇結(jié)構(gòu)，便于分析算法的性能及算法性能與簇結(jié)構(gòu)之間的關(guān)系。首先在多個合成數(shù)據(jù)上進行測試，然后在4個真實數(shù)據(jù)上實驗。由于各數(shù)據(jù)集已知類標簽，選擇兩個外部評價指標Macro-F1[13]和標準化互信息(Normalized Mutual Information, NMI)[20]來評估各種算法的聚類性能，指標的值越大表明聚類效果越好。

其中：F1(classk)為第k個簇的F1值；P(classk,ci)和R(classk,ci)分別表示數(shù)據(jù)集中真實的類classk與聚類結(jié)果中簇ci相比的準確率和召回率；classk表示數(shù)據(jù)集中第k個真實的類;nk表示classk包含的樣本點數(shù)。

NMI的計算公式如下：

其中：nij表示真實數(shù)據(jù)集中類i與聚類結(jié)果中簇j相一致的樣本點數(shù)目;ni表示屬于類i的樣本點數(shù)目;nj表示屬于簇j的樣本點數(shù)目;R表示真實類別數(shù)，實驗中設(shè)定K=R。

3.2 合成數(shù)據(jù)實驗結(jié)果

實驗中利用numpy中的random.multivariate_norma()函數(shù)合成三個數(shù)據(jù)集。由于二類數(shù)據(jù)可以直觀表現(xiàn)簇結(jié)構(gòu)，因此，在合成數(shù)據(jù)時，將簇數(shù)目固定為兩類；此外，使用方差σ衡量各簇中樣本的分布散度。合成數(shù)據(jù)的主要參數(shù)如表1所示。如表1所示，三個合成數(shù)據(jù)集的樣本數(shù)量逐個遞增，以此來驗證本文MCN算法在不同數(shù)據(jù)量下的性能表現(xiàn)；同時，注意到同個數(shù)據(jù)集不同簇之間樣本數(shù)量和樣本方差都有較大差異。三個合成數(shù)據(jù)集的數(shù)據(jù)維度也逐個遞增，以此測試不同數(shù)據(jù)維度下各算法的性能。

為直觀地展現(xiàn)合成數(shù)據(jù)中樣本的分布情況，將DS1投影到部分維度所確定的低維空間中，投影結(jié)果如圖2所示。從圖2可知，DS1中的多數(shù)類(樣本數(shù)量較多的簇)的數(shù)據(jù)分布較為分散，少數(shù)類的分布則較為集中，且兩個簇存在交疊現(xiàn)象。

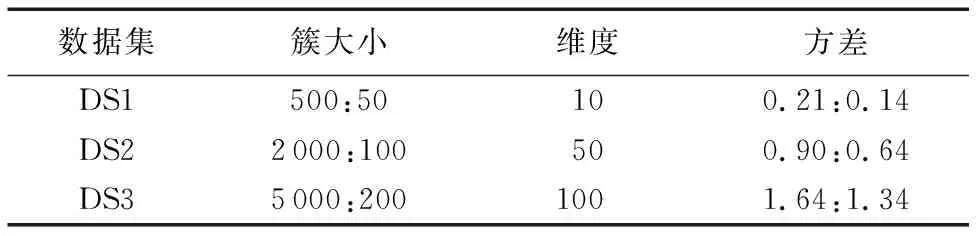
表1 合成數(shù)據(jù)集參數(shù)Tab. 1 Parameters of synthetic datasets

表2顯示不同算法在合成數(shù)據(jù)集上取得的聚類結(jié)果。如表所示，本文MCN算法的聚類精度和NMI值都優(yōu)于對比算法，表明MCN能更好地聚類此型非均勻數(shù)據(jù)。GMM算法在三個合成數(shù)據(jù)集上的NMI值均為0，這是因為GMM算法將數(shù)據(jù)中的所有樣本都劃分到同一個簇中，側(cè)面反映了基于經(jīng)典高斯模型的方法并不能有效處理非均勻數(shù)據(jù)。在兩個指標上，IFCM算法與GMM接近。Verify2的聚類精度最低，但與GMM和IFCM算法相比，其NMI值有一定的提升，表明基于樣本抽樣的方法對非均勻數(shù)據(jù)聚類效果的改善有限。

表2 合成數(shù)據(jù)集不同算法聚類結(jié)果Tab. 2 Clustering results of different algorithms on synthetic datasets

不同算法在合成數(shù)據(jù)上的運行時間如表3所示。表3中，本文MCN算法的運行時間低于對比算法GMM、Verify2和IFCM。Verify2的運行時間遠高于GMM和MCN算法，一個主要原因是Verify2采用了譜聚類方法，涉及到矩陣特征值計算等，當樣本數(shù)量和數(shù)據(jù)維度較大時，其算法運行時間較長。

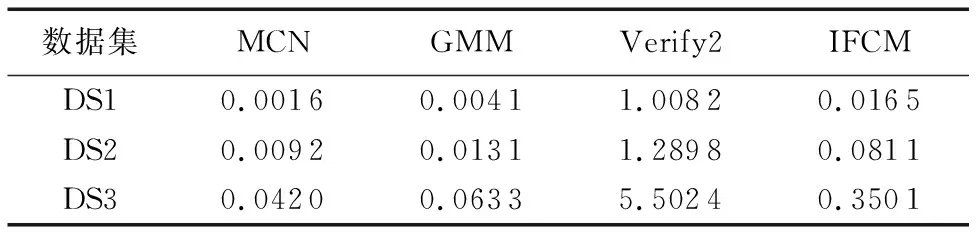
表3 不同算法在合成數(shù)據(jù)上的運行時間 sTab. 3 Running time of different algorithms on synthetic datasets s

表5 算法在實際數(shù)據(jù)集上的聚類結(jié)果Tab. 5 Clustering results of different algorithms on real-world datasets

3.3 實際數(shù)據(jù)實驗結(jié)果

實驗使用的實際數(shù)據(jù)來自聚類分析常用的UCI Machine Learning Repository(http://Archive.ics.uci.edu/ml/datasets.html)。選用了四個實際數(shù)據(jù)集：Breast Cancer Wisconsin(簡寫為BCW)、Wine、 ForestType和Ionosphere，數(shù)據(jù)集主要參數(shù)如表4所示。其中，BCW為乳腺癌診斷數(shù)據(jù)，包含241個惡性樣本和458個良性樣本；Wine是相關(guān)研究常用的不平衡數(shù)據(jù)集，其普通品質(zhì)酒類的樣本數(shù)較多，而品質(zhì)較好和品質(zhì)較差的樣本數(shù)量則較少；ForestType是森林遙感數(shù)據(jù)，包含三種不同的森林類型和一類空地，其中Sugi forest類的樣本數(shù)量較多；Ionosphere為電離層雷達波數(shù)據(jù)，其中具有某種特定結(jié)構(gòu)的樣本數(shù)量較多。這四個數(shù)據(jù)集中，不同簇類的樣本數(shù)有較大差異，且樣本分布(方差)也存在差異，是典型的非均勻數(shù)據(jù)。實驗將基于BCW、 Wine數(shù)據(jù)集驗證各種算法在低維數(shù)據(jù)上的性能，在ForestType、Ionosphere上對比算法在較高維度數(shù)據(jù)上的表現(xiàn)。本文MCN算法與對比算法在四個實際數(shù)據(jù)上的聚類結(jié)果如表5所示。表5顯示，MCN算法在Wine數(shù)據(jù)上的兩項指標稍低于IFCM算法，但在其他數(shù)據(jù)集上的聚類精度和NMI值都明顯優(yōu)于對比算法，表明MCN算法可以有效聚類實際應(yīng)用中的非均勻數(shù)據(jù)。

表4 實際數(shù)據(jù)集參數(shù)Tab. 4 Parameters of real-world datasets

如前所述，本文提出的MCN算法可以實現(xiàn)非均勻數(shù)據(jù)的子空間聚類,實現(xiàn)途徑是在聚類過程中自動地賦予每個特征以不同的權(quán)重。下面以Wine數(shù)據(jù)集為例，從MCN算法的一次聚類結(jié)果中提取特征權(quán)重信息，作進一步分析。圖3顯示該數(shù)據(jù)集中三個簇(分別記為Cluster1、Cluster2和Cluster3)各自的13個特征(分別命名為A1,A2,…,A13)的權(quán)重分布。

圖3 Wine數(shù)據(jù)中三個簇的特征權(quán)重分布Fig. 3 Distribution of feature weights of three clusters in dataset Wine

如圖3所示，不同簇的特征權(quán)重分布并不相同。例如，對于Cluster3，MCN算法賦予A11(指“酒的色調(diào)”)較大的權(quán)重，這表明“色調(diào)”對識別Cluster3有重要的作用；而特征A8(一種稱為“Nonflavanoid phenols”的酚類化學(xué)物質(zhì))對Cluster2中酒的品質(zhì)有較大影響。以上結(jié)果表明，MCN算法可以有效識別特征對于不同簇類有差別的貢獻度，從而提高了實際應(yīng)用中非均勻數(shù)據(jù)聚類的性能。

4 結(jié)語

針對K-means型算法的“均勻效應(yīng)”問題，本文提出了MCN算法。首先分析了經(jīng)典K-means算法隱含使用的概率模型，它是基于有關(guān)參數(shù)為常數(shù)這一假設(shè)的高斯混合模型，此簡化模型并不能很好地刻畫非均勻數(shù)據(jù)簇之間樣本數(shù)量和密度都有較大差異的特點。接著，從概率模型角度入手，結(jié)合軟子空間聚類技術(shù)定義了一種非均勻數(shù)據(jù)簇的概率模型，并推導(dǎo)出了相應(yīng)的聚類優(yōu)化目標函數(shù)。最后給出了MCN的算法過程。在合成數(shù)據(jù)和實際數(shù)據(jù)上的實驗結(jié)果表明，與GMM、Verify2、IFCM等算法相比，MCN算法在多數(shù)情況下都可以取得較大的聚類性能提升，從而驗證了本文所提算法的有效性。

在大數(shù)據(jù)時代如何結(jié)合大數(shù)據(jù)處理工具分析非均勻數(shù)據(jù)是一項有意義的工作，因此下一步將結(jié)合分布式Spark平臺進一步研究非均勻數(shù)據(jù)聚類新方法。