基于MEMS陀螺儀輔助的粒子群優(yōu)化磁力計校正

原雨佳，王 偉，陳興邦

(哈爾濱工程大學自動化學院，哈爾濱 150001)

0 引言

磁力計是一種測量磁場強度的儀器，通過對其三軸分量的計算能夠得到導航中重要的航向角信息，具有無累計誤差的優(yōu)點。然而磁力計有不可忽視的零位、靈敏度、非正交誤差，以及周圍環(huán)境影響造成的軟硬磁誤差，這些都會造成其輸出不準確，從而影響解算航向角的精度。因此，在使用前需要對其進行誤差分析，并采用有效的算法進行補償校正，提高其實用性。

目前針對磁力計校正的算法有很多。橢球擬合法是一種常見的磁力計校正算法，它不需要其他輔助信息，依據(jù)將未校正的橢球分布的磁力計數(shù)據(jù)還原成球型的原理實現(xiàn)校正。雖然此種算法原理簡單、計算量小，但是它需要空間中各個方向的采樣數(shù)據(jù)，操作復雜[1-3]。極大似然估計法同樣不需要輔助信息，但它對初值的選取有較高的要求，而且計算量大[4-6]。除了以上兩種無姿態(tài)的離線校正算法，工程中更為常用的是利用非線性卡爾曼濾波算法實現(xiàn)對誤差參數(shù)的在線校正，該算法具有良好的實時性，但是難以預估傳感器的濾波初值和噪聲分布[7-9]。為了解決傳統(tǒng)磁力計校正算法中采樣點多和初值條件嚴苛等問題，武元新提出了將粒子群優(yōu)化(Particle Swarm Optimization，PSO)算法用于磁力計校正中，此種算法使用更加精準的非線性誤差模型，并且無需良好的初值[10]。之后他對此算法進一步優(yōu)化，提出了增強型粒子群優(yōu)化(Stretching Particle Swarm Optimization，SPSO)算法，避免了粒子過早陷入局部最優(yōu)，但是運算時間長[11]。目前的PSO算法多數(shù)采用校正前后的磁場總量不變作為適應(yīng)函數(shù)，只能用于磁力計簡化模型，需要假設(shè)傳感器至少有一個軸與載體系重合，從而將12個未知參數(shù)簡化成9個或6個參數(shù)進行求解[12-13]。

針對傳統(tǒng)PSO算法用于磁力計校正中估計參數(shù)個數(shù)少的問題，本文提出了一種基于微機電系統(tǒng)(Micro-Electro-Mechanical System，MEMS)陀螺儀輔助的粒子群優(yōu)化算法對磁力計進行校正，為了避免算法過早陷入局部最優(yōu)，并且在動態(tài)環(huán)境中具有較好的適應(yīng)性，采用了隨機漂移粒子群優(yōu)化算法[14]。通過理論仿真和實測數(shù)據(jù)證明，該算法能夠有效地補償磁力計誤差，具有更好的工程實用性。

1 磁力計誤差模型

根據(jù)對磁力計的靈敏度、零位、非正交以及軟硬磁誤差的分析，建立如下的磁力計誤差模型[15]。

(1)

其中：

S=SscSnoSsi

b=bm+bhi

(2)

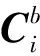
(3)

2 基于陀螺儀輔助的隨機漂移粒子群優(yōu)化算法

粒子群算法是一種仿效鳥類覓食過程的優(yōu)化算法，通過迭代不斷提高與目標函數(shù)有關(guān)的種群的候選解，即通過位置與速度更新公式尋找適應(yīng)目標函數(shù)的粒子，每個粒子的移動不僅受自身經(jīng)驗的影響，也受當前種群中最優(yōu)位置的影響。與其他算法相比，粒子群算法需要設(shè)置和調(diào)整的參數(shù)較少，而且收斂速度快，近些年發(fā)展迅猛。

2.1 目標函數(shù)

粒子群濾波中有2個重要的極值，一個是粒子個體最優(yōu)值，用Pbest表示，另一個是種群的全局最優(yōu)值，用Gbest表示。算法的目的就是尋找Gbest使目標函數(shù)值最小。假設(shè)待解決問題的粒子維數(shù)為D，種群中粒子個數(shù)為m，在第k次迭代中，第i個粒子的位置向量可以表示為：

Pi(k)=(pi1(k),pi2(k),pi3(k),…,piD(k))T

(4)

速度向量可以表示為：

Vi(k)=(vi1(k),vi2(k),vi3(k),…,viD(k))T

(5)

從磁力計誤差模型中可以看出，校正算法的目的就是求解公式中的S和b，所以每個粒子可以用如下的數(shù)學式表示：

(6)

其中：

(7)

從誤差模型上可以看出，各種誤差對各軸向產(chǎn)生的影響是不同的，在有陀螺儀輔助的情況下，通過陀螺儀解算姿態(tài)角信息，在已知地磁場的情況下得到理想載體系下的磁場矢量，此磁場矢量應(yīng)與磁力計補償后的磁場矢量相同。由此可以建立磁場矢量適應(yīng)函數(shù)，將其寫為下面的數(shù)學表達式

F2,i=argminf2(S,b)

(8)

2.2 隨機漂移粒子群優(yōu)化算法

傳統(tǒng)PSO算法在一定的迭代后，粒子速度會慢慢減小，使得種群收斂到某個最優(yōu)值，一旦環(huán)境發(fā)生變化，失去多樣性的種群很難對此做出快速響應(yīng)。在實際磁力計使用中，周圍有不可避免的磁性物質(zhì)，這些都會對磁力計輸出造成影響，因此，本文采用一種具有較強全局搜索能力的隨機漂移粒子群優(yōu)化(Rondom Drift PSO，RDPSO)算法。受金屬導體內(nèi)自由電子運動模型的影響，通過將最優(yōu)值的搜索過程類比于自由電子向具有最小勢能位置的運動，從而提高算法的搜索能力[16]。

該算法的具體流程為：

1)粒子群初始化

初始化粒子個數(shù)m，粒子維數(shù)D，權(quán)重的最大值ωmax和最小值ωmin，最大的迭代次數(shù)kmax，速度限制的最大值Vmax和最小值Vmin，位置限制的最大值Pmax和最小值Pmin。按照式(9)初始化粒子速度和位置。

Pi,j(k=0)=Pminj+rand(0,1)(Pmaxj-Pminj)

Vi,j(k=0)=Vmin+rand(0,1)(Vmax-Vmin)

(9)

式中，Pminj和Pmaxj分別是每個粒子第j維對應(yīng)的位置最大值和最小值，對于磁力計校正，前9維對應(yīng)的位置限定范圍要小于后3維偏置對應(yīng)的位置范圍，這樣設(shè)置可以為濾波算法提供更實用的初值。

在初始化階段，粒子的個體最優(yōu)Pbesti(k=0)≡Pi(k=0)，通過式(8)計算每個粒子的適應(yīng)值，選擇最優(yōu)的位置為種群最優(yōu)值Gbest。

2)粒子群更新

與傳統(tǒng)PSO算法速度更新方式不同，RDPSO算法中粒子運動包括兩部分，即定向漂移運動和無規(guī)則隨機熱運動，數(shù)學表達式為：

Vij(k+1)=Vrij(k+1)+Vdij(k+1)

(10)

式中，k是迭代次數(shù)，i(i=1,2,3,…,m)表示粒子群中第i個粒子，j(j=1,2,3,…,D)表示粒子的第j維，Vrij(k+1)表示無規(guī)則隨機熱運動，Vdij(k+1)表示定向漂移運動。

熱運動可以表示成：

Vrij(k+1)=α|Mj(k)-pij(k)|φij(k)

(11)

其中：

(12)

(13)

(14)

式中，α是熱系數(shù)，表征算法的全局搜索能力，本文改變其為固定常數(shù)的情況，設(shè)置為隨迭代次數(shù)增加而減小的S型函數(shù)，數(shù)學表達式為式(12)。Mj(k)是種群粒子個體歷史最優(yōu)位置的平均值，數(shù)學表達式為式(13)。φij(k)是正態(tài)隨機分布函數(shù)，s和uij(k)是(0,1)之間的2個不同隨機數(shù)，采用式(14)求解。

粒子的定向漂移運動可以定義為：

Vdij(k+1)= rand(0,1)c1(pbestij(k)-pij(k))+

rand(0,1)c2(gbestj(k)-pij(k))

(15)

式中，c1和c2分別是自我認知和社會認知,分別代表粒子自身位置最優(yōu)和種群位置最優(yōu)的影響；rand(0,1)是(0,1)之間的隨機數(shù)。

綜上，RDPSO算法的粒子速度和位置公式為：

vij(k)=α|Mj(k)-pij(k)|φij(k)+

rand(0,1)c1(pbestij(k)-pij(k))+

rand(0,1)c2(gbestj(k)-pij(k))

(16)

pij(k+1)=pij(k)+vij(k+1)

(17)

按照上式對粒子的速度和位置進行更新，同時在更新過程中限制速度和位置在所定范圍內(nèi)。

3)搜索全局最優(yōu)

因為本文中的問題是解決最小值問題，因此種群的目標就是找到最小的適應(yīng)值，對于每個粒子，如果新的適應(yīng)值小于Pbest對應(yīng)的適應(yīng)值，則更新當前位置的Pbest，否則Pbest不變。可以將Pbest寫為：

(17)

同樣的，如果新的Pbest對應(yīng)的適應(yīng)值小于此時Gbest對應(yīng)的適應(yīng)值，則更新Gbest，否則Gbest不變。可以將Gbest寫為：

(18)

其中，f是目標函數(shù)，即式(8)。

4)迭代

迭代停止的方法有兩種：種群的適應(yīng)值達到設(shè)定的最小值；迭代次數(shù)達到最大。本文使用的是第二種方法，如果迭代超出kmax，則迭代停止，此時的Gbest就是要求解的參數(shù)矩陣。

由此可見，此算法就是通過迭代追蹤個體歷史最優(yōu)值和種群歷史最優(yōu)值，其流程圖如圖1所示。

3 仿真實驗分析

本算法使用的環(huán)境是在哈爾濱市，依據(jù)IGRF12模型[17]計算當?shù)氐牡卮艌鍪噶繛镠i=[242.367;-46.225;-465.459]mG2。為了測試本算法的性能，分別做了以下幾個仿真模擬實驗。

3.1 參數(shù)估計數(shù)量對比實驗

為了比較本文所提算法與傳統(tǒng)PSO算法的參數(shù)估計數(shù)量，模擬磁力計分別繞X、Y、Z軸旋轉(zhuǎn)一周產(chǎn)生的數(shù)據(jù)，設(shè)置采樣周期為0.01s，從生成的3000個點選取均勻分布的30個點，陀螺儀漂移設(shè)為6.25(°)/h，具體的參數(shù)設(shè)置如表1所示。分別使用傳統(tǒng)PSO算法和本文所提算法進行校正，校正結(jié)果如表2所示。

表1 粒子群優(yōu)化算法參數(shù)設(shè)置表

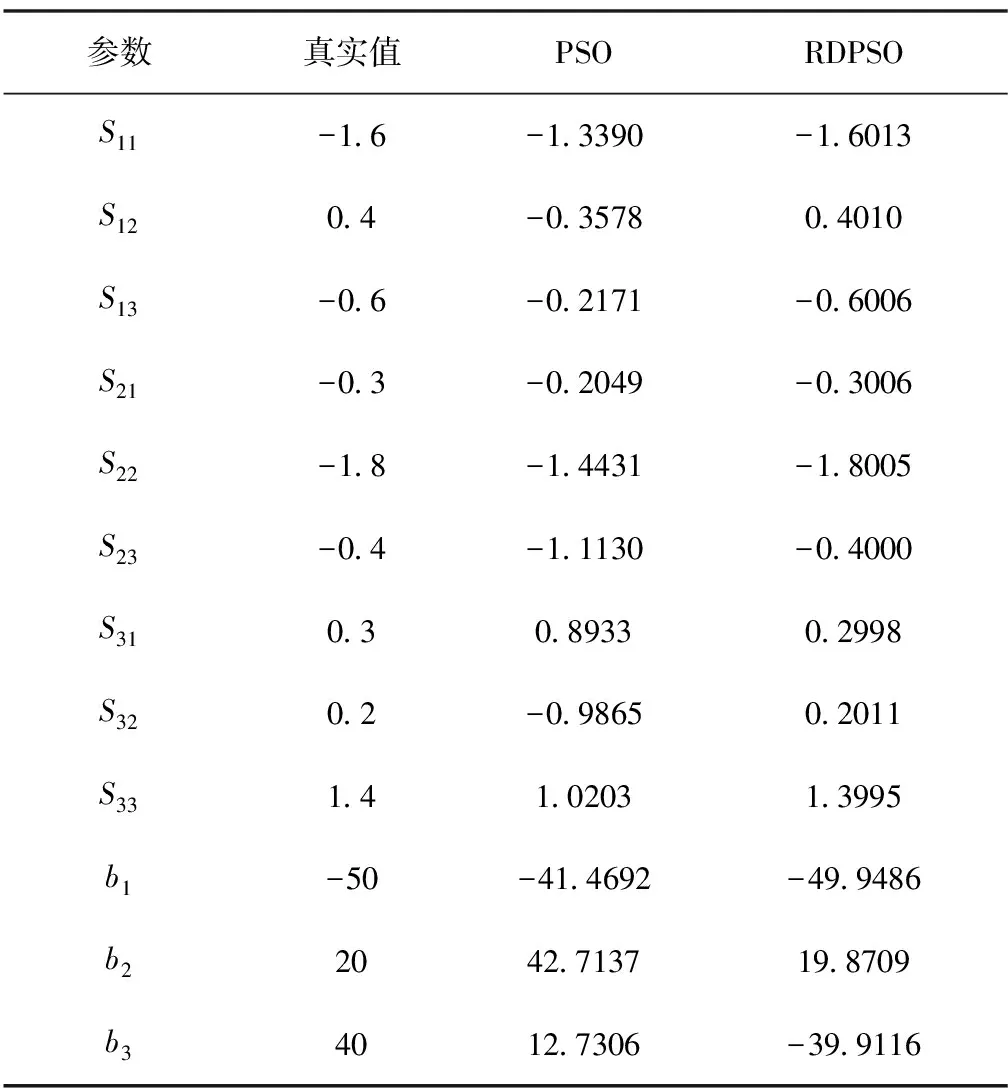
表2 12個誤差參數(shù)估計結(jié)果

從表中可以看出，使用傳統(tǒng)算法無法準確地估計出磁力計誤差模型中的12個參數(shù)，有些參數(shù)的估計結(jié)果與參考值相差較大。這是因為傳統(tǒng)算法只選用約束磁場總量的目標函數(shù)，沒有考慮磁場的三軸分量，造成當誤差矩陣S陣為9個不同參數(shù)時，粒子群尋找最優(yōu)值受到較大干擾。而本文提出的RDPSO算法卻能得到較為精準的參數(shù)估計結(jié)果。

3.2 旋轉(zhuǎn)度測試實驗

為了簡化校正中操作的復雜度，該實驗通過模擬磁力計的幾種不同旋轉(zhuǎn)方式，驗證算法在各種旋轉(zhuǎn)度下的性能。旋轉(zhuǎn)方式如下：

方式一：模擬磁力計在繞X、Y、Z軸各旋轉(zhuǎn)1周，即在空間中是3個完整的圓形；

方式二：模擬磁力計繞X、Y軸各旋轉(zhuǎn)1周，即在空間中是2個完整的圓形；

方式三：模擬磁力計繞X、Y軸各不完整旋轉(zhuǎn)1周，即在空間中是2個不完整的圓形；

方式四：模擬磁力計繞Z軸旋轉(zhuǎn)1周，即在空間中是1個完整的圓形。

針對四種不同旋轉(zhuǎn)方式獲取的采樣點，采用RDPSO算法進行校正，得到的參數(shù)估計結(jié)果如表3所示。

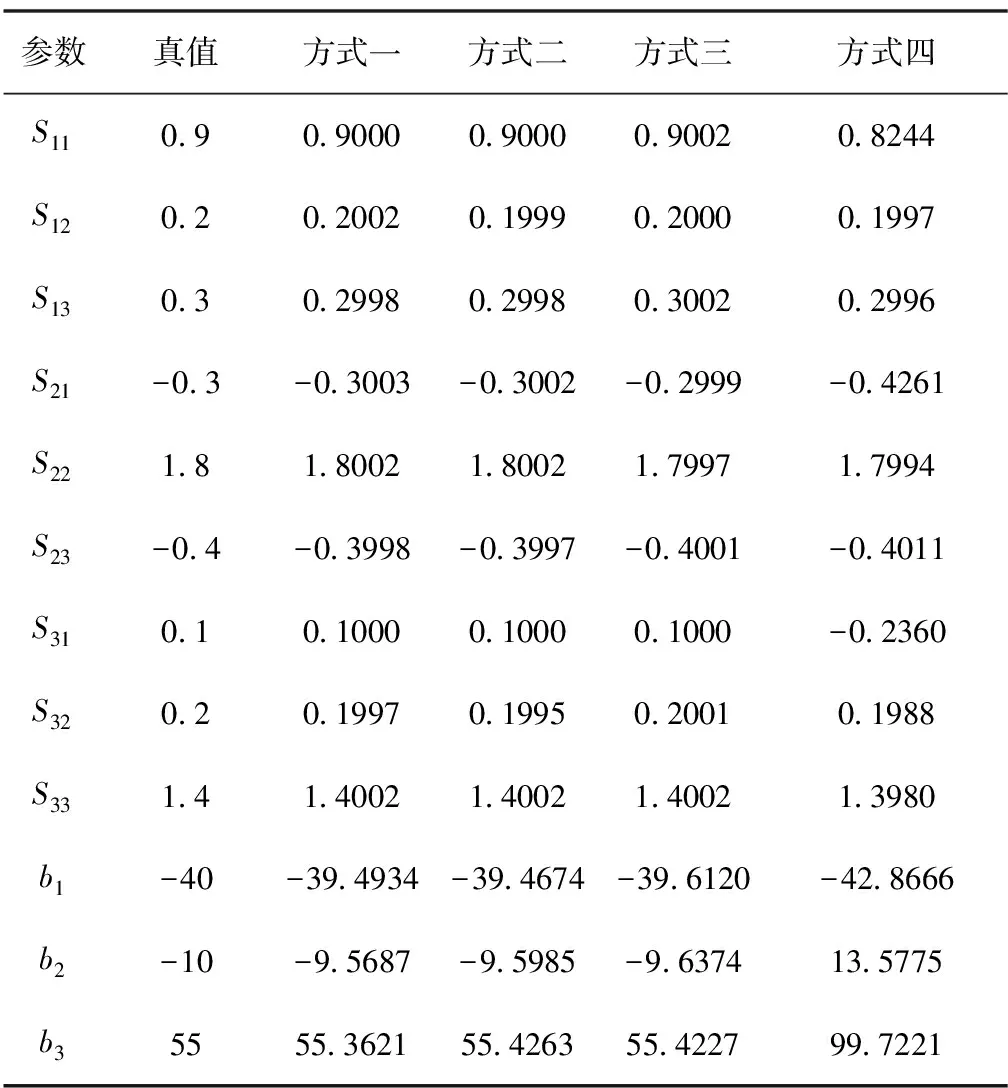
表3 各種旋轉(zhuǎn)度測試結(jié)果

從表3中可以看出，當采樣點在空間分布為不完整2周時，本文所提算法就能夠估計出磁力計誤差參數(shù)，與空間分布為完整3周時校正精度接近。但如果單獨繞一軸旋轉(zhuǎn)，即采樣點空間分布為平面1周時，由于粒子的多樣性過低，無法估計出磁力計12個誤差參數(shù)，尤其是對偏置矩陣無法估計。因此，本文所提算法只需要磁力計在空間中繞X、Y、Z中的任意2個軸不完整旋轉(zhuǎn)1周即可實現(xiàn)對誤差參數(shù)的估計，相對于傳統(tǒng)算法大大簡化了操作的復雜度。

圖2～圖4所示為磁力計分別旋轉(zhuǎn)完整3周、完整2周及不完整2周時，磁力計校正前后的采樣點分布圖。理想情況下，采樣點應(yīng)該分布在以地磁場強度為半徑的球上，但由于各種誤差的干擾使其偏離。從圖中可以看出，校正前的采樣點都在球面外側(cè)，經(jīng)過本文算法校正使其重新分布在球面，說明本算法能夠?qū)Υ帕τ嬚`差進行有效補償。

3.3 動態(tài)性能測試實驗

為了測試本文所提算法在磁場動態(tài)環(huán)境中的性能，做了以下的仿真實驗。模擬所在磁場環(huán)境是變化的，即不再設(shè)定磁場強度為一個定值，仿真中將其設(shè)置為線性變化的，得到的實驗結(jié)果如表4所示。

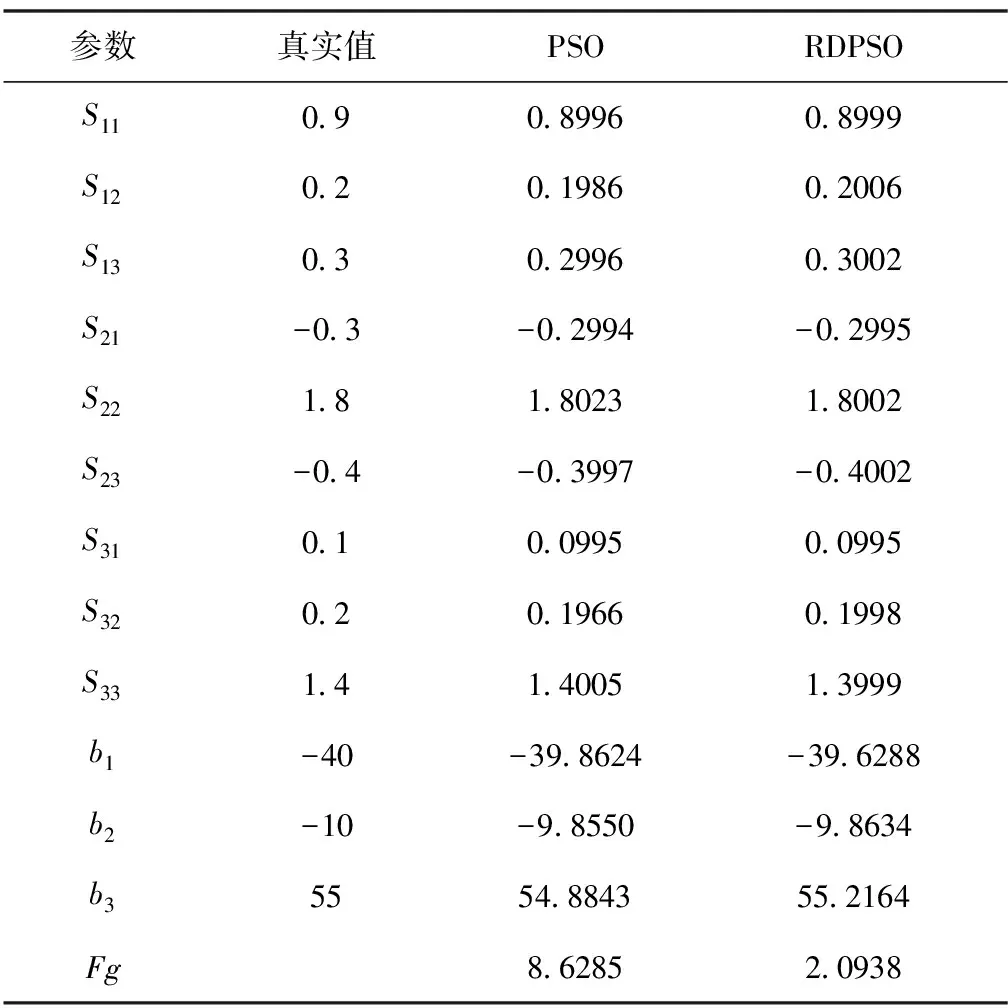
表4 動態(tài)性能測試結(jié)果

Fg是當粒子為最優(yōu)位置時，適應(yīng)函數(shù)的值，即通過式(8)得到的值，可以表征算法的精度。因此，可以看出，在磁場變化時，本文所提算法比傳統(tǒng)算法的精度高，說明本文所提算法具有更高的動態(tài)適應(yīng)能力。

3.4 陀螺儀精度影響測試實驗

為了驗證不同陀螺儀精度對算法精度的影響，本文針對幾種常見的陀螺儀精度做了仿真實驗，得到的結(jié)果如表5所示。

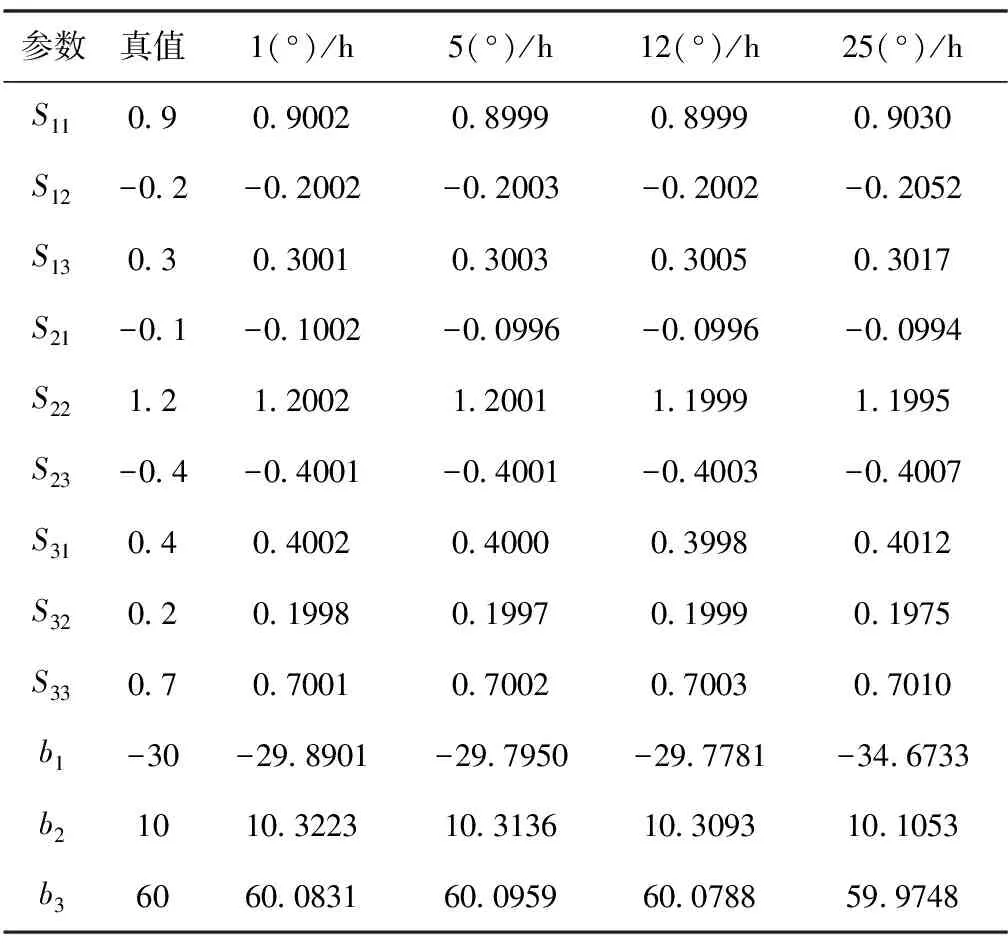
表5 陀螺儀精度影響測試結(jié)果

從表5可以看出，陀螺儀的精度會對本文算法造成影響，但是影響較小。

4 實測實驗驗證

為了驗證該算法在實際中的有效性，選用以ADIS16488為核心的MEMS-IMU系統(tǒng)作為實驗設(shè)備，實物如圖5所示，它的參數(shù)如表6所示。用ADIS16488 MEMS-IMU系統(tǒng)采集數(shù)據(jù)，同時為了降低陀螺儀誤差對算法精度造成的影響，取陀螺儀靜態(tài)數(shù)據(jù)的平均值作為零漂減去，再采用本文所提算法、PSO算法和擴展卡爾曼濾波(Extended Kalman Filter，EKF)算法對磁力計校正，得到的參數(shù)估計結(jié)果如表7所示，利用本文算法得到的磁力計校正前后數(shù)據(jù)的對比如圖6所示。從表中可以看出，本文所提算法精度最高，說明本算法在實際系統(tǒng)中能夠?qū)崿F(xiàn)磁力計的校正。

表6 ADIS16488參數(shù)

表7 不同算法參數(shù)估計結(jié)果

5 結(jié)論

1)解決了傳統(tǒng)粒子群優(yōu)化算法用于磁力計校正時需要簡化誤差模型，同時粒子容易陷入局部最優(yōu)的問題；

2)磁力計的誤差參數(shù)利用陀螺儀提供的角速率信息，建立補償前后的磁場矢量適應(yīng)函數(shù)，再迭代尋找粒子的全局最優(yōu)值求解；

3)仿真與實測實驗表明，只要將磁力計繞其三軸中的任意兩軸旋轉(zhuǎn)不完整一周即可估計磁力計的12個誤差參數(shù)，相對于傳統(tǒng)算法操作簡單、動態(tài)性好；

4)僅針對陀螺儀零位漂移對算法精度產(chǎn)生的影響進行了仿真實驗，并沒有對陀螺儀各種誤差進行詳細的分析；

5)本文算法僅能進行離線估計，需進一步研究在線估計磁力計誤差參數(shù)及陀螺儀誤差，提高算法的工程實用性。