基于EMD的小波神經網絡模型預測大壩變形

王玉振

(河南水利與環境職業學院，河南鄭州450008)

及時獲取大壩變形的演變規律并作出準確預報，對大壩安全具有重要意義[1]。由于大壩變形受溫度、水壓和時間效應等諸多因素影響，呈現出高度的非線性和非平穩性，難以建立較為準確的變形量與影響因素之間復雜的關系模型，因此，預測效果不佳[2]。目前，繼BP(Back Propagation，BP)神經網絡之后的小波神經網絡(Wavelet Neural Ntworks，WNN)模型被廣泛用于非線性、非平穩性時間序列預測，其結合了小波變換和人工神經網絡各自的特點，具備極強的自學習能力和小波變換局部化等優點[3]，能夠有效解決局部極小值問題。但在實際應用中發現，其存在小波分解無法實現的自適應多分辨率分析問題[4-5]。而經驗模態分解法[6-7](Empirical Mode Decomposition，EMD)在信號處理和分析中具有自適應的良好特性，能夠有效彌補小波神經網絡自適應多分辨率分析的不足。本文考慮影響因素對大壩變形的影響，并采用組合模型的思想，將經驗模態分解法和小波神經網絡相結合，充分發揮兩者各自的優勢，將有望對大壩變形中隱含的特征信息進行多層次、多角度挖掘和分析，從而提高預測精度。

1 基于EMD的小波神經網絡預測模型

1.1 經驗模態分解原理

EMD是N.E.Huang等人提出的一種信號分解技術，無須預先設定基函數，就可以自適應地將非平穩、非線性時間序列中的的波動和趨勢分離開，形成若干個固有模態分量IMF和1個余項，其實質是平穩化數據處理。對于任意一變形時間序列S(t)，對其進行經驗模態分解，步驟參照文獻[8]。因此，原始序列可以表示為

(1)

式中，S(t)為原始數據監測信號；t=1，2，3，…，m為時間采樣序列，其中，m為采樣總次數；IMFi為分解所得的第i個IMF分量；i=1，2，3，…，n為IMF分量的次序，是按頻率由高到低依次排列；B為單調殘余函數(EMD分解后的趨勢分量)。

1.2 游程判定法重構原理

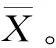
1.3 預測模型及流程

大壩變形的影響因素分為水位、溫度、時效三部分，設大壩在不同時間段的變形序列為{Y(x)=(tx，Hx，Tx)，x=1，2，…，n}，其中，t為時效量；H為上游水位影響因子；T為溫度影響因子。經EMD對大壩變形原始數據Y分解得到n個IMF和一個剩余量B，然后通過游程判定法對各分量進行重構得到高頻項F1、中頻項F2和低頻項F3，設對應的預測值分別為E1、E2和E3，模型預測流程如圖1所示，則最終的預測值

G=E1+E2+E3

(2)

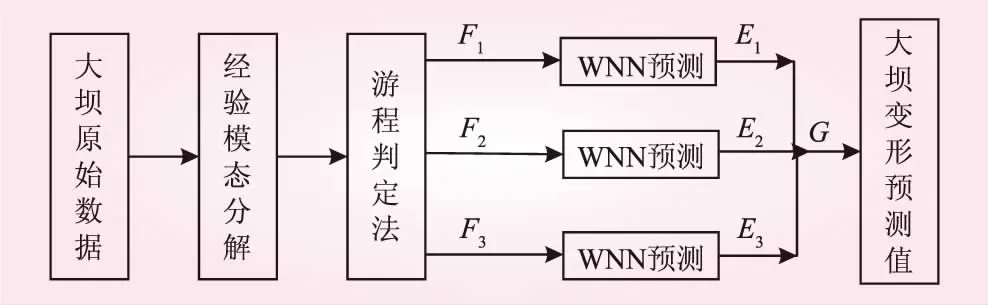
圖1 模型預測流程

1.4 模型精度評定

為了評價各模型預測性能的優劣，本文采用均方根誤差(Root Mean Square Error，RMSE)和平均絕對誤差(Mean Absolute Error，MAE)作為模型評價指標。

平均絕對值誤差(MAE)

(3)

均方根誤差(RMSE)

(4)

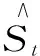
2 算例

2.1 實驗數據獲取及分析

本文以豐滿大壩30號壩段1985年1月4日～1987年6月22日的壩頂水平位移及同期庫水位、溫度和時效的實測資料為例[10]，共140期觀測數據，建立模型進行分析，如圖2所示。

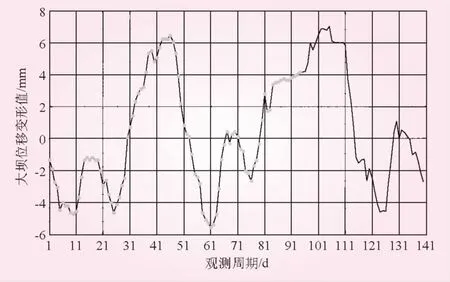
圖2 大壩變形水平位移序列

由圖2可見，該大壩變形較劇烈，無明顯規律可循，若直接建立模型進行預測分析，很難得到可靠的結果。本文先采用EMD對其進行預處理，分解結果見圖3。

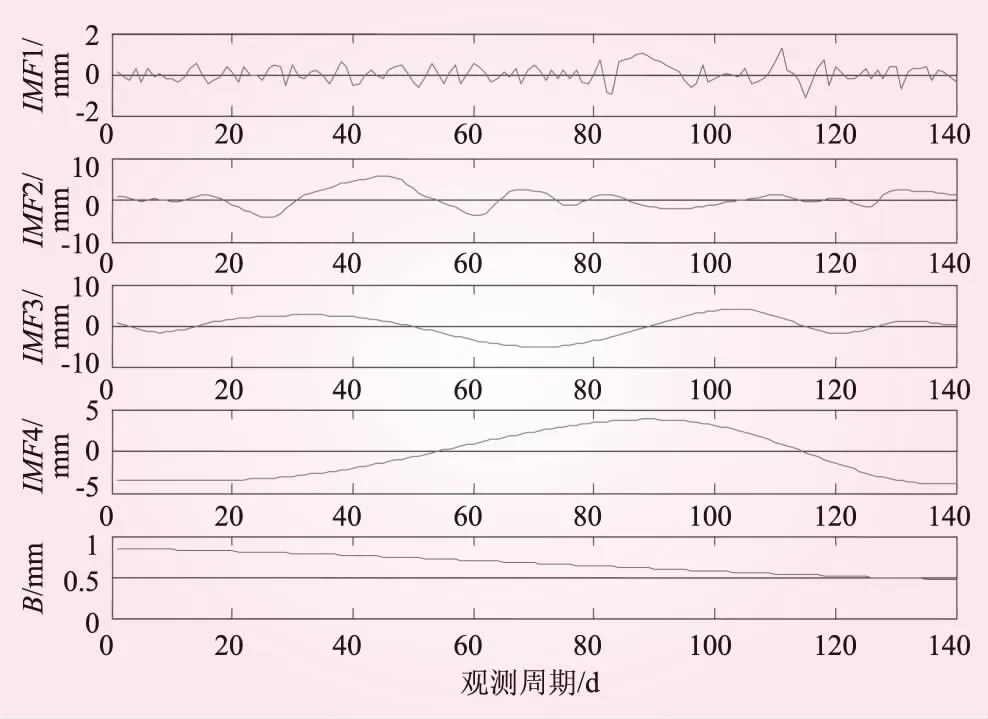
圖3 EMD分解結果

由圖3可知，EMD將變形序列自適應分解為4個IMF和一個殘余分量B，使各分量變化曲線比原來變形曲線(圖2)更光滑和平穩。EMD可以降低其非平穩性，將相同和類似信息獨立出來，有利于模型的建立和分析。但經EMD分解得到的分量個數多，會增加建模次數。因此，有必要采用游程判定法對各分量進行波動程度分析。IMF1、IMF2、IMF3、IMF4、B的游程總數分別為66、15、7、3、2。

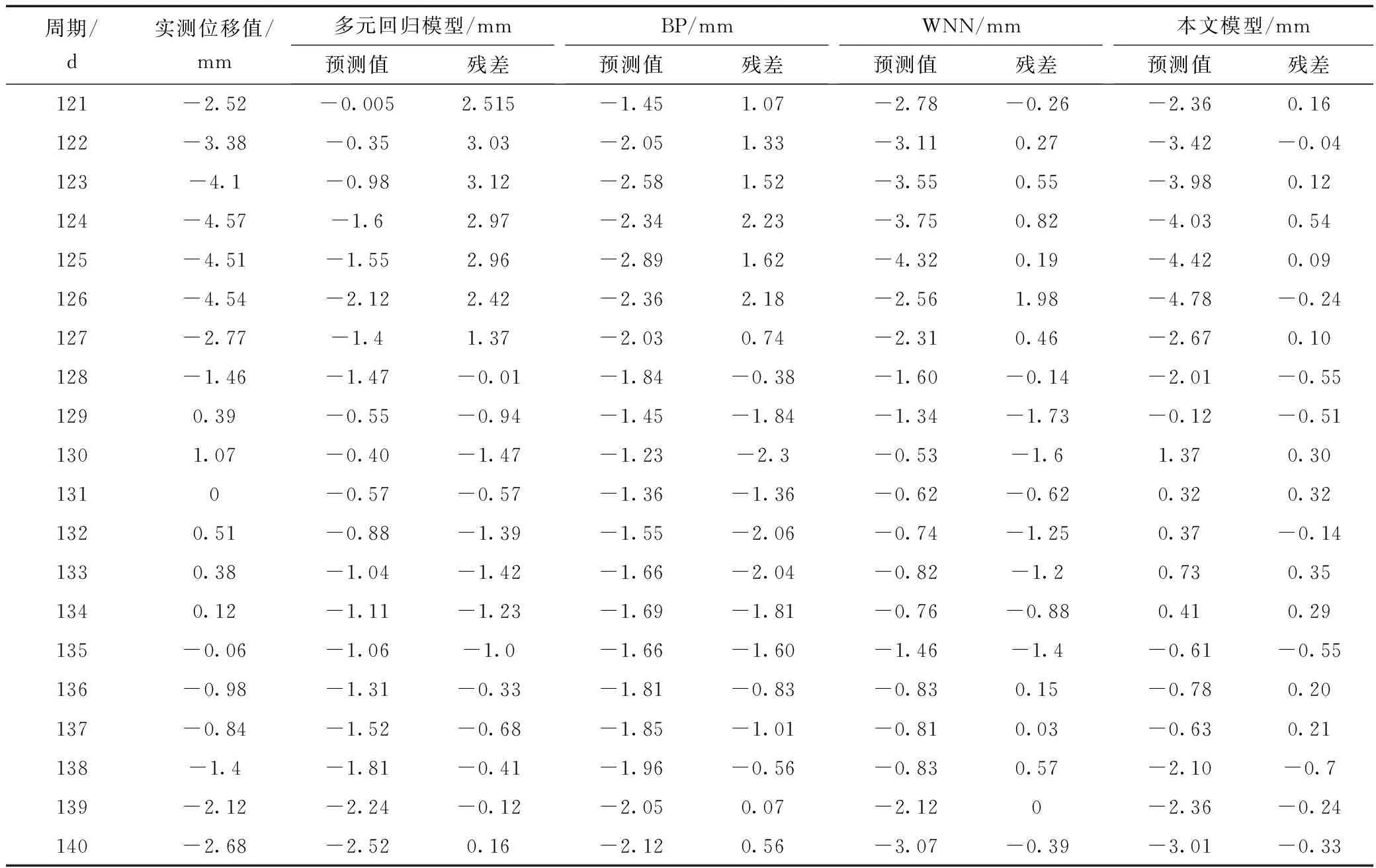
表1 各模型預測結果與實際值對比

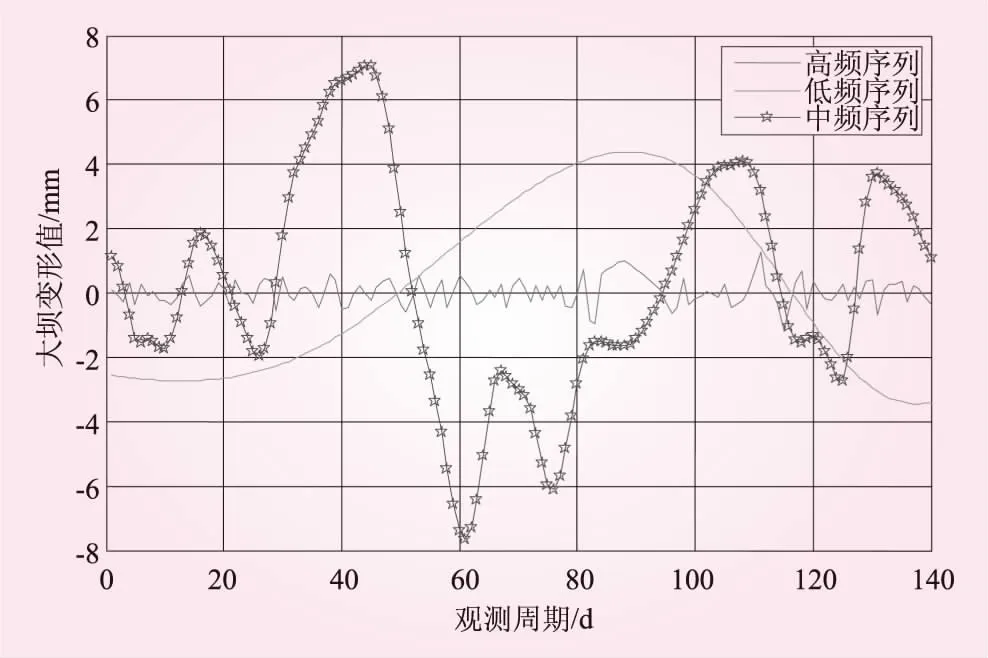
圖4 重構結果

由于游程總數反映出各分量的波動程度，所以將IMF1作為高頻分量，IMF2和IMF3疊加作為中頻分量，IMF4和余量B作為低頻分量。重構結果如圖4所示。

經重構后，可以減少建模次數和簡化數據處理過程，提高預測效率。為驗證本文算法的可行性和有效性，建立4種方案進行對比分析：①方案1。多元回歸模型。②方案2。BP神經網絡模型。③方案3。WNN模型。④方案4。基于EMD的小波神經網絡大壩變形預測模型。

2.2 預測結果對比分析

本文分別利用WNN訓練和測試經EMD分解重構后的高、中和低頻分量，并疊加各個預測值即為最終大壩變形預測結果，各模型預測結果見表1。

由表1可知，本文模型求出的殘差較小，最大殘差為0.7 mm，最小只有0.04 mm，其余殘差都小于1 mm，而其他模型的殘差均有大于1 mm的情況，不能保證較好的全局預測精度。因此，本文模型能較好地表達大壩變形分量與其影響因素之間復雜的關系，預測值與實際值吻合最好，均優于其他模型，預測精度較高。為了更直觀地探討各模型的預測效果，將各模型的預測值與大壩變形的真實值進行對比分析，見圖5。

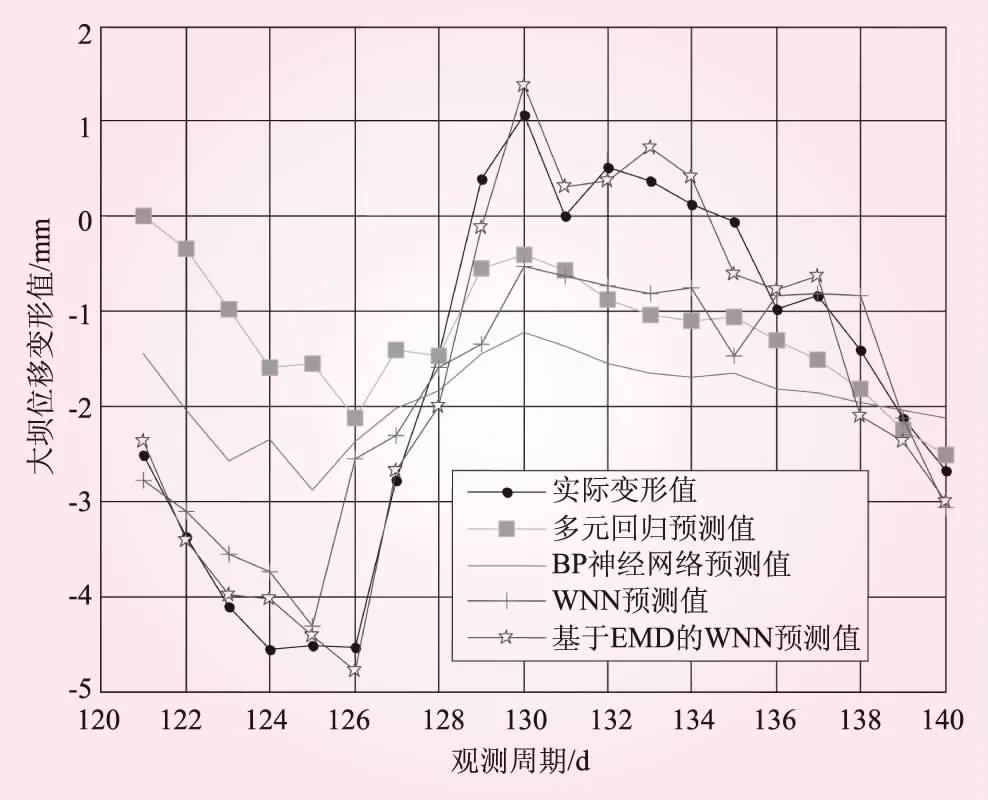
圖5 各模型預測結果與實際對比

由圖5知，方案1、2和3預測不穩定，部分預測值與實際值相比偏差較大，尤其在變形幅度較大的第121到127期、129到135期，波動比較大。而方案4的預測值與實際值吻合最好，表明基于EMD的小波神經網絡預測模型能較好地反映大壩變形規律，說明EMD能自適應地分析和提取變形時間序列中隱含的特征信息，將相同或類似的信息獨立出來，使得模型的自身性得到充分發揮，有效地彌補了小波神經網絡無法實現自適應多分辨率分析的不足，取得了較好的效果。同時，采用游程判定法將相同或相似波動程度的信息重新組合，減少了建模次數，提高了預測效率。為了進一步探討各模型的預測效果，各模型預測精度見表2。

由表2可看出，多元回歸、BP和WNN模型精度指標較差，不能很好地表達大壩變形與其影響因素之間復雜的函數關系。而本文利用EMD對大壩變形原始數據進行分解，能有效挖掘其內部規律，建立影響因素與變形分量之間復雜的關系模型，預測精度均優于WNN、BP和多元回歸模型，具有較好的泛化能力，可信度較高。這是由于EMD與WNN的結合，充分發揮了兩者各自的優勢，提高了預測精度。綜上，說明有必要先對非線性、非平穩時間序列進行EMD分析，這為大壩變形預測研究提供了一種新思路。

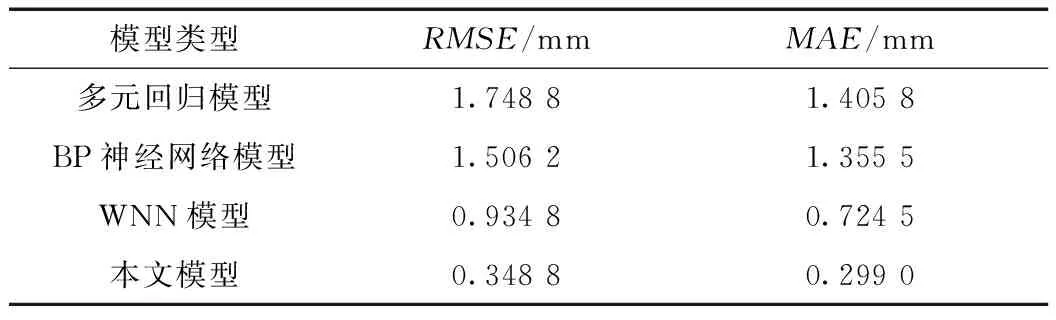
表2 各模型精度對比

3 結 語

目前，WNN是時間序列預測方法中較為理想的一種預測方法，但是其具有在預測中無法實現自適應多分辨率分析的不足，而利用EMD可以解決此問題。本文提出一種基于EMD的小波神經網絡大壩變形預測模型，經理論和算例分析，并與多元回歸、BP神經網絡和WNN模型對比分析表明，該算法預測精度較高，可以用于大壩變形預測。