滿子范疇的反變有限性與同調滿同態

連穎穎，彭 楨，沈 燕

(1.安陽師范學院 數學與統計學院，河南 安陽 455000；2.安徽大學 數學科學學院，安徽 合肥 230601)

反變有限子范疇的概念是由Auslander等[1]于1980年提出的.此后，Auslander等[2]對反變有限子范疇做了進一步的推廣，研究了由代數A的投射維數有限的有限生成模構成的滿子范疇p<∞(A)的反變有限性，且其與投射維數不超過1的傾斜模之間存在緊密的聯系.這些研究引起了代數學家的關注并在后續研究中得到了很多重要結論，如Angeleri-Hügel等[3]證明了對于有限維代數A，其有限維數有限當且僅當存在一個A上的傾斜模T，使得T的右正交滿子范疇與p<∞(A)的右正交滿子范疇一致，給出了著名的有限維數猜想的一個充要條件[4].這些研究使得對于p<∞(A)的反變有限性的研究有了一定的理論價值.

導出范疇的概念是由Grothendieck在20世紀60年代提出并由Verdier完成了其核心構造[5].自該概念被提出以來，導出范疇與許多學科產生了緊密的聯系，如偏微分方程、李理論、幾何以及代數等.在代數表示理論中，代數的導出范疇之間的等價給出了代數的一種等價關系，是代數之間的3種重要等價關系之一，它保持代數的許多同調性質，如導出等價保持K理論[6]、保持代數的有限維數的有限性等[7].此外，導出等價與穩定等價也聯系緊密[8].而環的同調滿同態誘導了兩個環的導出范疇之間的粘合，可以看作導出等價的推廣，它在代數表示理論和代數K理論等的研究中起到了重要作用.作者考慮同調滿同態能不能保持代數的一些性質，為代數工作者進一步討論代數的關系提供了一定的理論基礎.

論文研究了p<∞(A)的反變有限性在代數的導出等價下的關系，證明了p<∞(A)的反變有限性是導出等價下的不變量.

定理1給定域k上的有限維代數A,B，設存在同調滿同態：φ:A→B，如果B作為A-模是投射維數有限的，且p<∞(A)在A中反變有限，那么p<∞(B)在B中反變有限.

1 預備知識

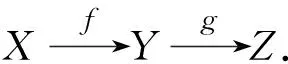
給定一個k-代數A,B，對于代數同態φ:A→B，若滿足給定任意的代數同態f1,f2:B→C滿足φf1=φf2，都有f1=f2,則稱φ是一個滿同態，顯而易見，代數之間的滿同態其實是代數范疇內的一個滿態射.

引理1[9]設φ:A→B是一個代數同態，則下列各條等價

(1)φ是一個滿同態；……