偽極小內射半模

曾慧平，吳 蕾，王海威

(南昌航空大學 科技學院，江西 南昌 330034)

半環是最常見的代數結構，它在拓撲學、分析學、最優化理論、計算機科學中都有極其重要的作用.與環論中利用環上模研究環構造一樣，利用半環上的半模研究半環構造是十分重要而行之有效的方法. Johnson等[1]給出了半模的定義后，內射半模有了許多形式的推廣，如極小內射半模[2]、p-內射半模[3]、擬內射半模與偽內射半模[4]等.論文繼續引入偽極小內射半模的概念.在對這一新半模類進行研究時，主要探索有關偽內射半模與相對極小內射半模的部分性質對于偽極小內射半模是否仍然成立，并且給出偽極小內射半模的其他相關性質與等價刻畫.

論文中的R均表示含零元和單位元的加法交換半環.如果不特別聲明，所有的半模U都是指滿足條件u·1=u,?u∈U的右R-半模.S=End(UR).記rR(u)={r∈R|ur=0}，其中：u∈U；lU(r)={u∈U|ur=0}，r∈R.對任意的X?U，A?R，rR(X)=∩x∈XrR(x)，lU(A)=∩a∈AlU(a).A≤U,A≤⊕U分別表示A是U的子半模和直和項.

(i) 稱右R-半模U的非空子集A是可減的，當且僅當若u+u′∈A，u∈A，有u′∈A,?u,u′∈U；若U的任意子半模都可減，則稱U是完全可減半模．

(ii) 若半模U是由它的單子半模族(Uα)α∈A張成的，則?B?A，使得U=⊕BUβ，即U是半單半模.

(iii) 若U是半單半模且是完全可減半模，則稱U是半單優半模.

文中其他未提及的概念同文獻[2-9]一致.

定義1一個右R-半模U稱為右偽極小內射半模，是指對于U的任意極小子半模uR及任意半模單同態f:uR→U，都可擴張至U的自同態.

類似地可定義左偽極小內射半模.

定理1設R是半環，下列命題等價：

(1) 右R-半模U是偽極小內射半模；

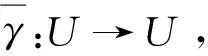
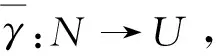
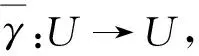
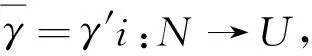
(3)?(1).令N=U即可.

定理2半單優半模是偽……