基于PSCAD/EMTDC的復轉矩系數法的時域實現及對電氣阻尼影響的研究

北京信息科技大學自動化學院，北京 100192

一、引言

電力系統次同步振蕩（Sub-synchronous Oscillation,SSO）是指電力系統受到擾動導致偏移其平衡點后，電網與汽輪發電機組之間在一個或多個低于系統同步頻率的固有頻率交換能量而產生的一種狀況或現象[1]。

近幾年來，我國一些大型電廠采用較高串聯電容補償度的對網輸電模式。由于存在串補輸電、交直流混合輸電系統導致的次同步振蕩，對電網和發電機組造成重大威脅。

對SSO的分析方法主要有頻率掃描法、特征值分析法、復轉矩系數法等。

頻率掃描法主要是定性分析與篩選發電機組，篩選出存在次同步振蕩風險的機組，計算方法比較簡單、易懂且快速，但缺點是誤差比較大[2]；

特征值分析法是小擾動分析法，其優點是理論嚴密、分析準確度高，但缺點是存在嚴重的“維數災難”；

復轉矩系數法是在特征值分析法的基礎上發展起來的方法，由I. M. Canay 提出[3]，并建立了包括電氣、機械兩部分的扭振方程以及穩定性判據，它也是基于系統線性化原理的一種方法，但比特征值分析方法簡單，主要用于分析電力系統次同步振蕩和軸系扭振[4-5]。

本文基于PSCAD/EMTDC電磁暫態仿真平臺對復轉矩系數進行實現研究，為了提高仿真精度，對實現過程中作出了一些改進，并給出可參考的標準。以IEEE第一標準測試系統為研究模型，分析了線路串聯電容補償度對電氣阻尼的影響。

二、復轉矩系數法的基本原理

復轉矩系數法是一種頻域分析方法，其主要基于線性化模型。復轉矩系數法的原理如下：

典型大型汽輪機的發電機組軸系一般有6個質量塊，分別為發電機、勵磁機、高壓缸、中壓缸和2個低壓缸，通常把這些質量塊視為集中質量塊，每個質量塊之間為無質量的理想彈簧連接，形成多質量—彈簧系統，如圖1所示。通常發電機軸系運動方程為：

式中，δ—軸系質量塊電氣角位移，δ=(δ1δ2δ3δ4δ5δ6)T，其中，δ5為發電機轉子的電氣角位移；

ωi—軸系第i個質量塊的電氣角速度，其中，ω5為發電機轉子的電氣角速度；

ω0—運行狀態穩定下的發電機的角速度；

τ—軸系質量塊慣性時間常數矩陣，τ=diag(τi,τ2,τ3,τ4,τ5,τ6)；

T—軸系質量塊的轉矩矩陣，T=(T1T2T3T4T5T6)T；

K—發電機軸系的彈性系數矩陣，其中，Ki,i+1為相鄰質量塊之間的彈性系數；

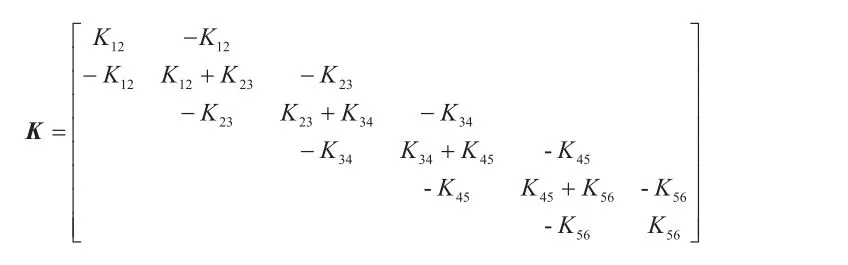
D—發電機軸系的阻尼矩陣，其中，Dii為第i個質量塊的自阻尼系數，Di,i+1為相鄰質量塊之間的互阻尼系數。

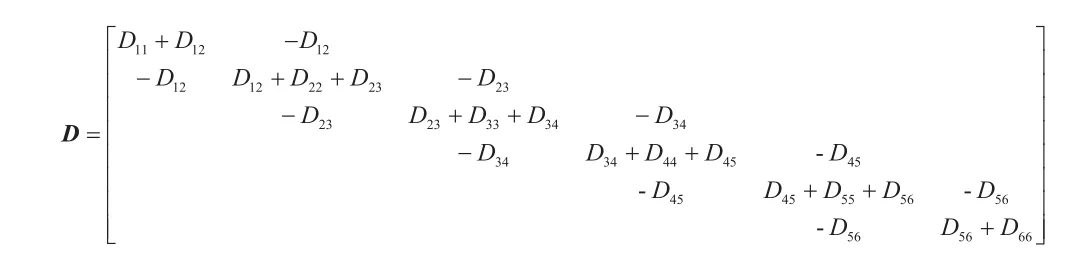
首先，在運行點進行線性化，之后可得：

Δδ—相鄰質量塊的電氣角位移差；

ΔTe—電磁轉矩增量；

ΔTM—機械轉矩增量。

忽略汽輪機出力變化，并消去發電機以外質量塊轉角可得：

式中，km(p) —機械轉矩系數；

Δδ5—發電機電氣角位移差。

定義等式（3）的第一項為“機械系統轉矩增量”，ΔTm(p)=km(p)Δδ5，其等效于軸系動態元件，與軸系相對應的一個虛擬轉矩增量，與式（2）中的ΔTM是兩個不同的概念。式（3）可以表示為：

如果電磁轉矩增量也滿足線性化條件，即可表示為：ΔTe(p)=ke(p)Δδ5，則式（4）表示為：

式中，ke(p) —電磁轉矩系數。

其次，同步頻率λ下的相量形式為：

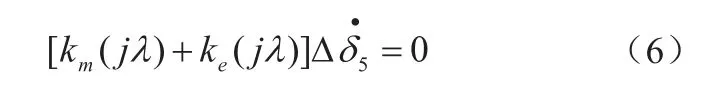
其中，km(jλ)—機械復轉矩系數；

ke(jλ)—電氣復轉矩系數；

則有：

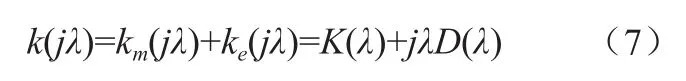
式中，k(jλ) —總復轉矩系數；

K(λ) —彈性系數，與轉角變化同相；

λD(λ)—阻尼系數，與轉速變化同相。

根據式（7）可以判定軸系的穩定性，其穩定判據為：

當D(λ)｜K(λ)=0>0 時， 軸 系 穩 定； 當D(λ)｜K(λ)=0=0 時，為臨界阻尼，臨界穩定。當D(λ)｜K(λ)=0<0 時，為負阻尼，軸系不穩定，將在頻率λ下產生發散振蕩。

對于系統中頻率為λ的振蕩分量，可以采用相量來表示前面的關系，即發動機電磁轉矩增量的相量形式為 ：

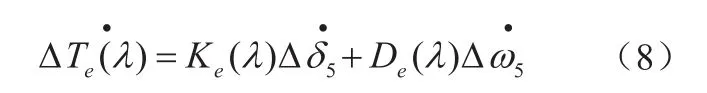
式中：Ke(λ) —電氣彈性系數；

De(λ) —電氣阻尼系數；

根據上述的穩定性判據時可知：當電磁轉矩增量ΔTe(λ)和發電機角速度增量Δω5兩者之間的相位在-90°～90°之間，即相位在右半平面時，對應的電氣阻尼系數為正值，則發電機軸系穩定。反之，當相位在左半平面時，電氣阻尼系數為負值，發電機軸系不穩定，將在次同步頻率λ下產生發散振蕩。

將式（8）變形，可以得到：

電氣阻尼轉矩系數De(λ)的值可以根據式（9）求解，即：

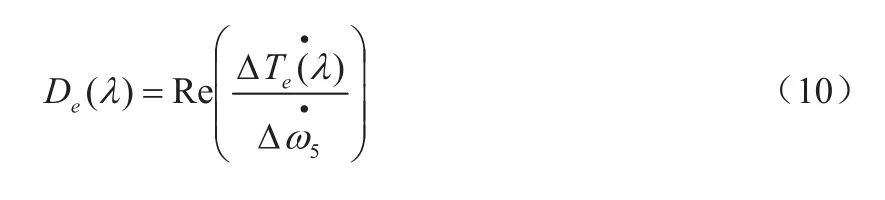
三、時域仿真實現步驟

根據定義可知，復轉矩系數可以分為電氣部分和機械部分，對于電氣復轉矩系數有兩種方法可以求出，一種方法是可以通過系統的傳遞函數得到，另一種方法是通過曲線計算得到，而機械復轉矩系數一般是利用系統的傳遞函數模型來計算，再根據穩定性判據來分析軸系是否穩定[4]。

由于次同步振蕩頻率遠離工頻，因此需要采用電磁暫態仿真軟件PSCAD/EMTDC來計算復轉矩系數。

PSCAD/EMTDC是一種時域仿真計算軟件，其計算原理為：首先對電力系統中表示每個元件中機械和電氣特性的微分方程，將其轉化成差分方程，再利用節點分析方法聯立，并采用固定計算時間步長來求解系統各運行變量在每一個計算時刻的瞬時值[6]。所采用的計算方法以隱式梯形積分法為基礎，該方法同時包括了后退歐拉法的計算方法，兩者結合達到了改善計算過程的數值穩定性的效果。

以計算電氣阻尼轉矩系數為例，來說明計算復轉矩系數的時域計算方法。系統要求發電機軸系模型采用單剛體模型，而且電氣部分采用完整的數學模型，具體時域仿真實現步驟具體如下[5]：

（1）利用電磁暫態仿真軟件PSCAD/EMTDC建立系統的電磁暫態仿真模型，并且調試成功；

（2）當系統運行狀態已經達到穩定后，在系統的發電機的轉子上即PSCAD所建模型的輸入端Tm施加一串頻率為f0整數倍的小幅脈動激勵轉矩：

式中，φk—給系統施加脈動轉矩的初相位；

Tk—給系統施加脈動轉矩的幅值，Tk要求值較小，如果太大的話，就會導致系統非線性化，不滿足假設條件。

（3）當待研究的系統運行狀態再次達到穩定后，截取脈動轉矩一個公共周期內的發電機電磁轉矩Te和發動機角速度ω；

（5）根據式（10）可以得到激勵頻率下的電氣阻尼轉矩系數De(kf0)，從而可以判斷系統的穩定性。

下面針對上述5個步驟依次討論和分析各步驟的具體執行。

四、系統仿真模型的建立

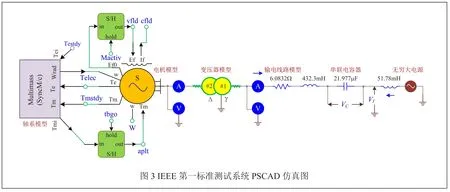
本文所研究的系統為IEEE第一標準測試系統，此系統主要用于次同步振蕩的研究，如圖2所示。系統主要以500kV的傳輸系統和892.4MVA的發電機組為基礎，其模型軸系含有6個質量塊，分別為勵磁機（EXC）、發電機（GEN）、高壓缸（HP）、中壓缸（IP）、2個低壓缸（LPA和LPB）。

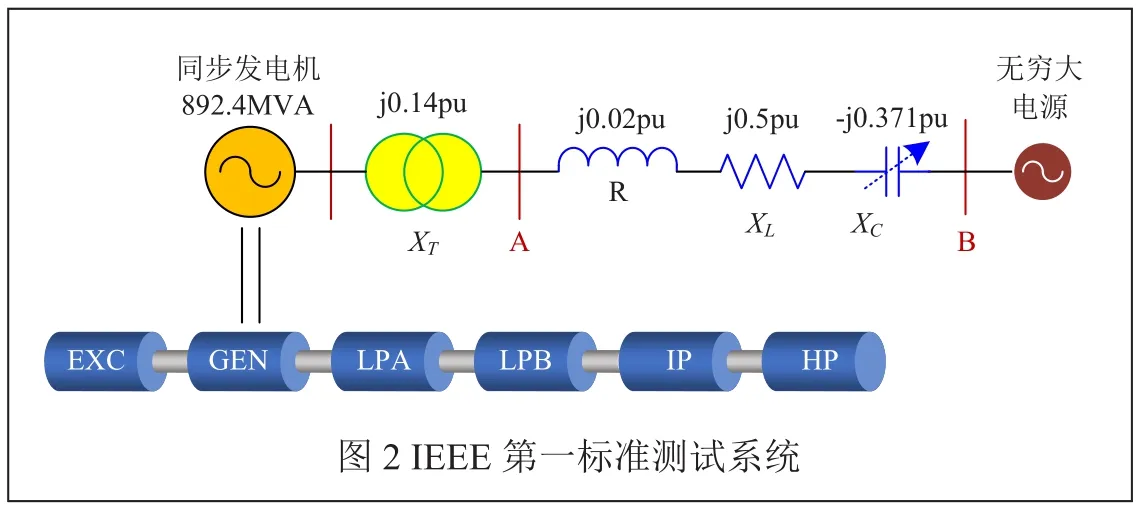
利用軟件PSCAD/EMTDC中提供的標準模型庫，建立如圖3所示的IEEE第一標準測試系統模型，其中包括發電機、串聯電容器、無窮大電源等模型，由于發電機軸系需要采用單剛體模型，發電機模型需要忽略多質量塊。在建模過程中，其相關參數值見參考文獻[6]，建模完整圖如圖3。

五、擾動模型的建立

幅值的大小會影響仿真精度，系統對接入的脈動轉矩幅值的要求較小，建議幅值為0.005～0.05之間，一般取0.01pu。如果幅值太大的話，就會破壞系統可線性化的前提條件。在加入脈動轉矩的時候，需要考慮兩個問題：

（1）如果每次只加入一個頻率值的小值脈動轉矩的話，既費時又統計困難；

（2）選擇一次性加入多個頻率不等的脈動轉矩時，則會造成各頻率值之間相互干擾的后果，如下式：

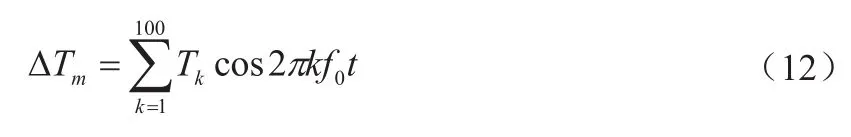
式中，f0—基頻。

這里取f0=0.5Hz，因次同步振蕩的頻率最大為50Hz，所以k最大取值為100，這樣加入脈動轉矩的方法會導致疊加后的幅值較大，從而破壞了系統的可線性化性。

綜合上述問題，本文提出的方法是：在對系統同時加入擾動轉矩前，先對各個頻率分量的轉矩進行處理，即加上一個滯后相位如下：

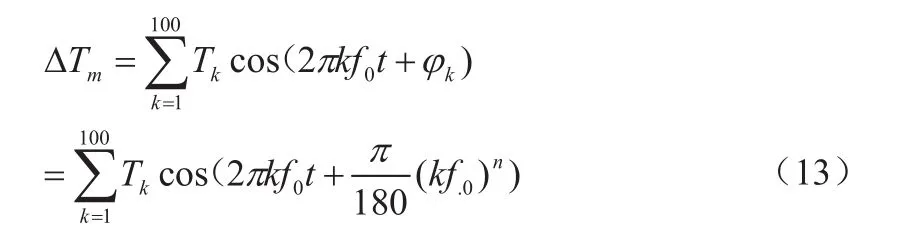
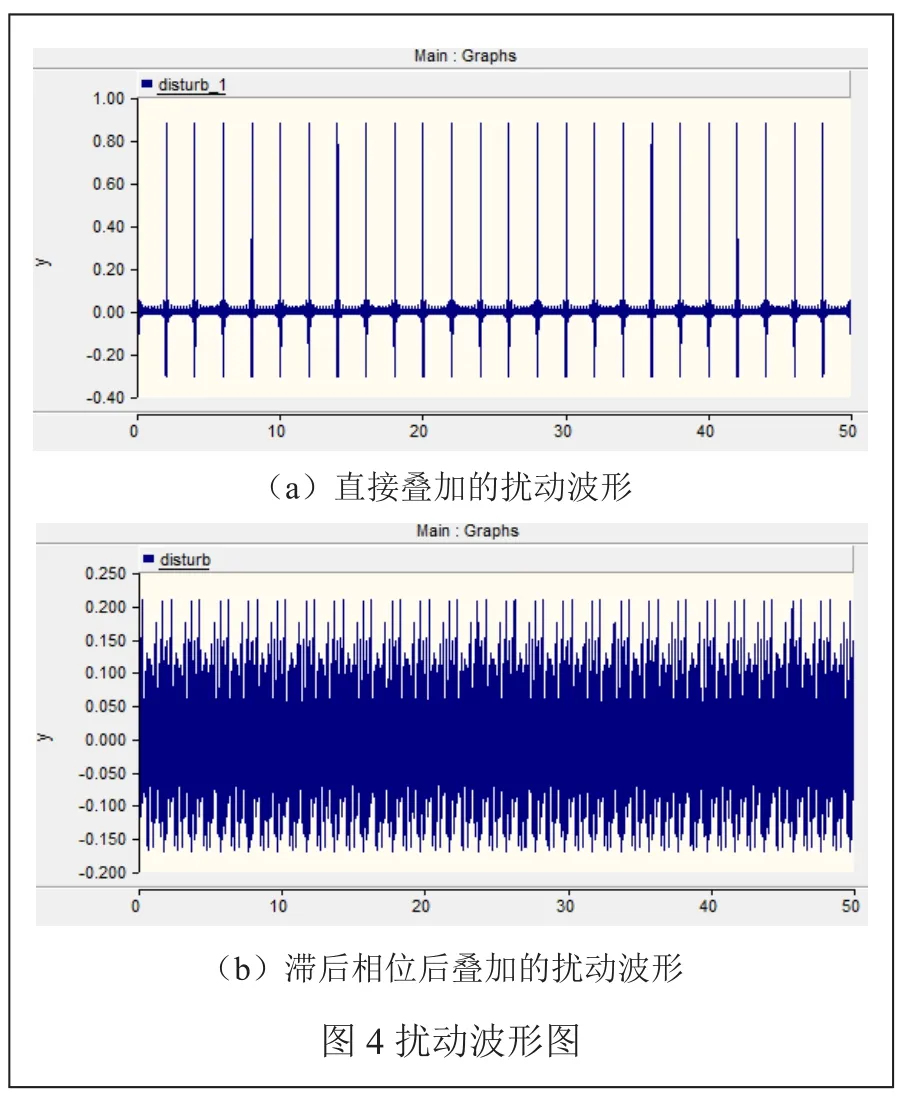
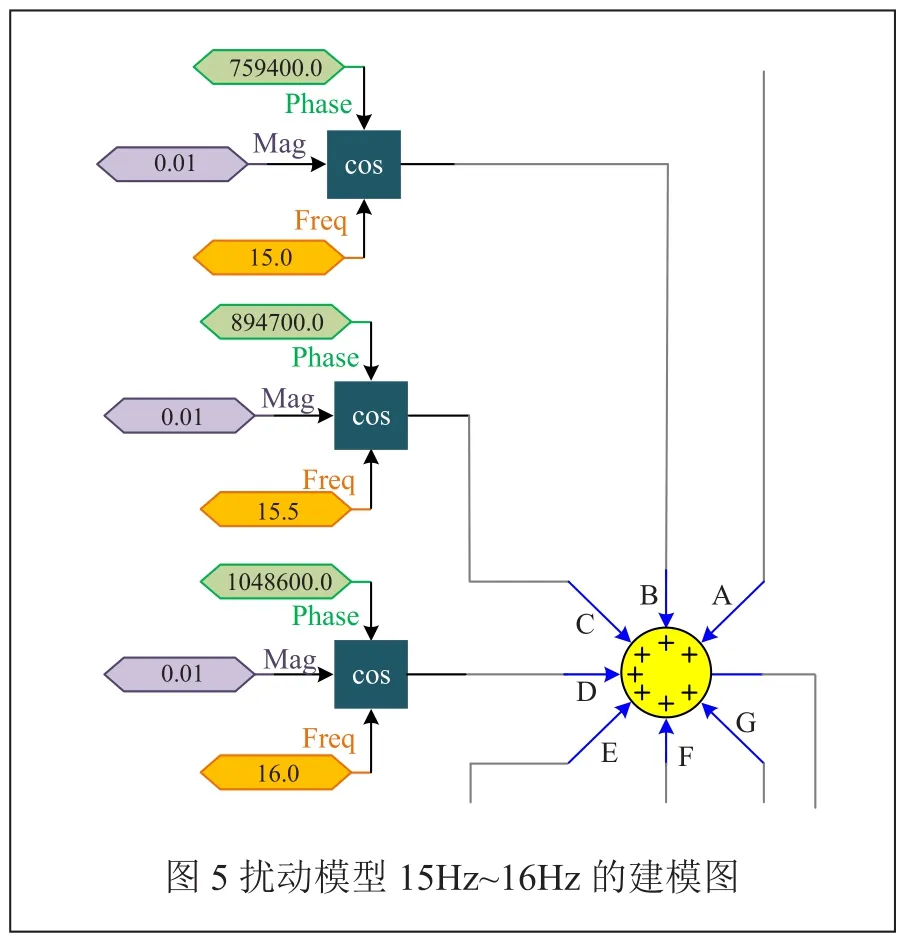
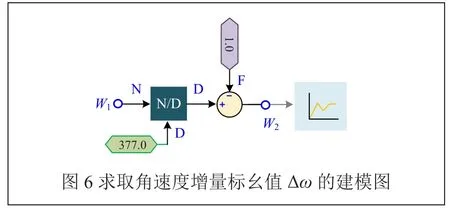
圖4是未加滯后相位的擾動波形和加了滯后相位的擾動波形對比圖。從圖中我們可以看出，未加滯后相位時，幅值已經達到0.8pu，不滿足要求。加了滯后相位之后，擾動量的幅值減小了4倍左右，并且沒有破壞系統的可線性化條件。等式（13）中的n值取為5，這樣疊加的擾動信號會比較平緩，不破壞系統的線性化條件。局部擾動模型細節見圖5，圖5中為擾動模型15Hz～16Hz的建模圖，其模塊中的三個輸入分別為Phase（相位）、Mag（幅值）、Frep（頻率）。

六、角速度增量標幺值Δω的求取

待系統運行狀態再次穩定之后，截取發電機同一個公共周期電氣轉矩Te和發電機角速度ω。本文所分析的算例中，系統的采樣頻率為1000Hz，即采樣公共周期為0.001s。軟件PSCAD/EMTDC中輸出的轉速ω即為發電機角速度的真實值，得到真實值之后要轉換成標幺值，再求取角速度增量的標幺值。在PSCAD上搭建模型求取Δω如圖6。圖6中，W1為輸出的發電機角速度的真實值，377.0為基準角速度值（設置工頻f=60Hz，則基準電氣角頻率為2πf=377rad/s ，產生發電機基準轉速真實值也為377rad/s），W2即為角速度增量的標幺值Δω：

七、Fourier分解以及電氣阻尼系數的求取

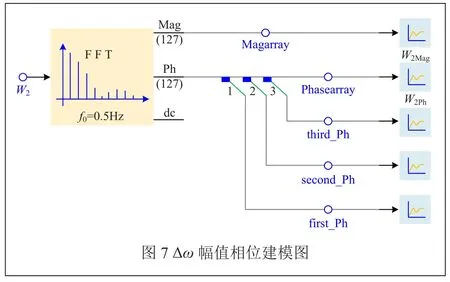
軟件PSCAD中的在線FFT模塊如圖7，可以用于Te和ω的Fourier分解，更直觀、實時地觀測每個頻率下幅值（A）和相位值（φ）。

以Δω為例，幅值相位建模如圖7所示。FFT模塊參數設置時，考慮到次同步振蕩頻率為5Hz～50Hz，所以參數設置的范圍要涵蓋次同步振蕩頻率范圍，即基頻f0參數設置為0.5Hz，對應的諧波數設置為127，則其頻率范圍為0Hz～63.5Hz，從0Hz～63.5Hz中選出滿足次同步振蕩的各個頻率分量。圖7中，輸出W2Mag和輸出W2Ph分別為各個頻率（0Hz～63.5Hz）下相對應的幅值和相位值，圖7中first-Ph、second-Ph、third-Ph分別是第一、二、三次諧波（即0Hz、0.5Hz、1Hz）對應的相位，這樣可以清楚地知道某一諧波對應的相位輸出圖，幅值也是類似。

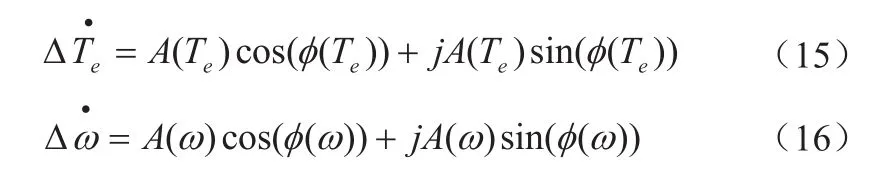
八、線路串補度對系統電氣阻尼的分析研究

針對IEEE第一標準測試系統，分析研究串補度對電氣阻尼的影響，固定其他參數不變的前提下，系統只改變串補電容值。取串補電容值分別為21.977μF、30.75μF、47.09μF，其所對應的串補度分別為74.1%、53%、34.6%，利用上述方法在待研發電機轉子上，從而可以得到電氣復轉矩曲線。三個線路串補度（74.1%、53%、34.6%）對應的電氣阻尼系數如圖8所示。

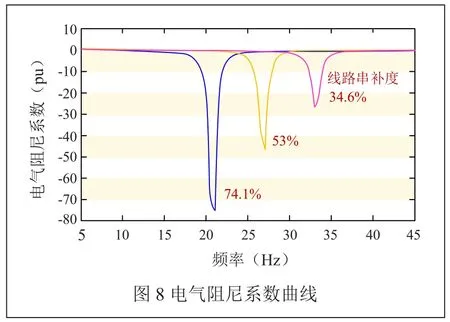
由圖8可見，當線路串補度為74.1%時，電氣阻尼系數在11Hz～29Hz區間為負，在21Hz附近達到最小值，由于機械系統的正阻尼一般比較小，因此系統的諧振頻率的總阻尼為負，則說明此系統存在次同步振蕩不穩定問題。其它兩種情況與此類似。

綜合可以看出，當線路串補度分別為34.6%、53%、74.1%時，串補度越大，系統阻尼系數峰值所對應的電氣頻率越低，電氣諧振點的負阻尼越大，則系統潛在發生次同步振蕩的危險性也就越高；反之，線路的串補度越低，系統阻尼系數峰值所對應的電氣諧振頻率越高，系統的電氣諧振點負阻尼越小，發生次同步振蕩潛在的危險性相對越低。但是如果線路串補度越低的話傳輸能力就會越小，因此應綜合考慮各方面的因素，選擇最合適的線路串補度。

九、結論

本文基于復轉矩系數法，運用電磁暫態仿真軟件PSCAD/EMTDC對復轉矩系數法進行了時域仿真實現，并作出一些改進，在實現過程中遇到的一些問題做了全面的分析并給出可參考的標準：

1、對于含串聯電容補償度的系統，系統接入脈動轉矩幅值的要求較小，建議取0.01pu左右。

2、考慮到快速性和滿足不破壞系統的線性化的假設條件下，在對系統同時加入擾動轉矩前，對各個頻率分量的轉矩都加上一個滯后相位。

最后以IEEE第一標準測試系統為分析模型，求取電氣復轉矩曲線，分析了線路串補度對電氣阻尼系數的影響，線路串補度的值與電氣諧振頻率成反比，即線路串補度越高，電氣諧振頻率會越低，對應的電氣諧振點的負阻尼也就越大，系統潛在發生次同步振蕩的危險性也就越高。