高斯混合模型下的相關(guān)子空間與離群數(shù)據(jù)挖掘

樊盼盼,張繼福

(太原科技大學(xué) 計(jì)算機(jī)科學(xué)與技術(shù)學(xué)院,太原 030024)

1 引 言

離群數(shù)據(jù)是數(shù)據(jù)集中可能包含一些數(shù)據(jù)對(duì)象,它們與數(shù)據(jù)的一般行為或模型不一致,蘊(yùn)含著大量不易被發(fā)現(xiàn)卻很有價(jià)值的數(shù)據(jù)[1],并已經(jīng)被廣泛運(yùn)用于電信[2]、災(zāi)難氣象預(yù)報(bào)[3,4]、金融[5,6]、網(wǎng)絡(luò)入侵檢測(cè)[7]等.隨著人們對(duì)離群數(shù)據(jù)挖掘重要性認(rèn)識(shí)的不斷加深,以及其離群數(shù)據(jù)挖掘越來越廣泛的應(yīng)用,日益受到重視,成為數(shù)據(jù)挖掘領(lǐng)域的研究熱點(diǎn)之一.在大多數(shù)情況下,離群數(shù)據(jù)與正常數(shù)據(jù)在局部數(shù)據(jù)集中的密度是存在差異的[8],有些屬性維上,密度差異較大(稀疏性),另一些屬性維上,密度差異比較小(稠密性),密度差異不明顯的屬性維對(duì)度量離群數(shù)據(jù)幾乎是無關(guān)的.因此,尋找和刪除高維數(shù)據(jù)集中密度差異較小的稠密子空間,可以有效地降低“維災(zāi)”的干擾,并能有效地發(fā)現(xiàn)隱藏的離群數(shù)據(jù).

相關(guān)子空間是一種與離群數(shù)據(jù)有關(guān)的屬性集維集合[9],可在相關(guān)子空間中有效地度量離群數(shù)據(jù),從而可有效地降低“維災(zāi)”的影響,但如何選擇和度量相關(guān)子空間是關(guān)鍵.現(xiàn)有相關(guān)子空間的選擇和度量都存在著時(shí)間復(fù)雜度高、依賴于數(shù)據(jù)分布、參數(shù)選擇等局限性.高斯混合模型是用高斯概率密度函數(shù)精確地量化事物,可以將一個(gè)將事物分解為若干的基于高斯概率密度函數(shù)的模型[21],可有效地識(shí)別高維數(shù)據(jù)集中密度差異較大(稀疏)的屬性集合和密度差異較小(稠密)的屬性集合,適用于不同分布的數(shù)據(jù).本文針對(duì)高維離群數(shù)據(jù),給出了一種相關(guān)子空間中的離群數(shù)據(jù)挖掘算法.該算法首先利用稀疏度和高斯混合模型,確定數(shù)據(jù)對(duì)象的相關(guān)子空間和不相關(guān)子空間,有效地避免稠密數(shù)據(jù)對(duì)挖掘精度和效率的影響;其次,在相關(guān)子空間中,利用各個(gè)數(shù)據(jù)的稀疏度和各個(gè)屬性維的權(quán)值來度量數(shù)據(jù)對(duì)象離群值,可以有效的降低“維災(zāi)”的干擾;然后,將離群值最大的若干個(gè)數(shù)據(jù)對(duì)象視為離群數(shù)據(jù);最后,采用人工數(shù)據(jù)集和UCI數(shù)據(jù)集實(shí)驗(yàn)驗(yàn)證了該算法正確性和有效性.

2 相關(guān)工作

傳統(tǒng)的離群挖掘方法,例如基于統(tǒng)計(jì)[15],基于距離[11,12],基于密度[13,14],基于角度[16]等,都會(huì)受到維度的影響,不適用于高維數(shù)據(jù),因此將數(shù)據(jù)投影到相關(guān)子空間上再度量離群數(shù)據(jù)是一種有效的離群挖掘方法.相關(guān)子空間法[8,9,17-20],是在數(shù)據(jù)集中,尋找與離群數(shù)據(jù)有關(guān)的屬性集合組成的相關(guān)子空間,然后在相關(guān)子空間中度量離群數(shù)據(jù),包括基于局部參考數(shù)據(jù)集的線性相關(guān)性[17,18],以及基于局部參考數(shù)據(jù)集的統(tǒng)計(jì)模型[8,9,19,20]等.

·線性相關(guān)性

Kriegel等人[17]提出了軸平行子空間離群挖(SOD)方法,該方法通過共享最近鄰居(SNN)為每一個(gè)數(shù)據(jù)對(duì)象尋找一個(gè)相似子集,并在相似子集中確定軸平行線性相關(guān)子空間,在 SOD 中,僅僅在一個(gè)相關(guān)子空間中來刻畫數(shù)據(jù)對(duì)象的離群程度,當(dāng)數(shù)據(jù)對(duì)象分布在兩個(gè)或兩上以上的子空間中時(shí),SOD 將不能區(qū)分它們的離群程度,顯然,在相關(guān)子空間中,采用歐式距離的維平均方法度量離群具有明顯的不足;Kriegel等人[18]以主成分方法為理論依據(jù),采用馬氏距離結(jié)合伽瑪分布的方法實(shí)現(xiàn)了離群數(shù)據(jù)挖掘,該方法得到的相關(guān)子空間是線性相關(guān)的任意子空間,相關(guān)子空間對(duì)線性分布的數(shù)據(jù)具有很好的適應(yīng)性,但由于該方法是基于對(duì)局部數(shù)據(jù)分布趨勢(shì)的偏離,當(dāng)離群數(shù)據(jù)所在稀疏區(qū)域體現(xiàn)出一種不明顯的相關(guān)性時(shí),由最大似然估計(jì)得到的相關(guān)子空間容易出現(xiàn)錯(cuò)誤.

·統(tǒng)計(jì)模型

Muller等人[8]利用柯爾莫哥洛夫-斯米爾諾夫檢驗(yàn)的統(tǒng)計(jì)方法,提出了在數(shù)據(jù)集上選擇有意義的子空間方法,從低維到高維采用遞歸的方式逐步尋找非均勻分布的子空間,并將數(shù)據(jù)對(duì)象在各個(gè)相關(guān)子空間中的局部離群值累乘,作為該數(shù)據(jù)對(duì)象最終的離群程度,解決了不同子空間中的離群因數(shù)可比性問題,但在該算法中,確定所有相關(guān)子空間具有維度指數(shù)級(jí)的時(shí)間復(fù)雜性,因此其效率較低,對(duì)高維數(shù)據(jù)集的維度可擴(kuò)展性差,無法適應(yīng)于海量高維數(shù)據(jù);Keller等人[19]利用蒙特卡洛方法尋找相關(guān)子空間集,該方法由數(shù)據(jù)對(duì)象對(duì)應(yīng)在每個(gè)相關(guān)子空間中的局部數(shù)據(jù)子集確定該數(shù)據(jù)對(duì)象的離群程度,但該相關(guān)子空間實(shí)際上是從全局的角度考慮得到的;Sathe S等人[20]利用隨機(jī)哈希的方法,提出了一種有效的子空間的離群檢測(cè)方法,該方法能夠大大降低時(shí)間復(fù)雜度,對(duì)海量的數(shù)據(jù)有著很好的適用性,但該方法不適用于挖掘局部的離群數(shù)據(jù);張繼福等人[9,22,23]利用局部稀疏差異因子,通過預(yù)先設(shè)定好的閾值對(duì)每個(gè)維度上稀疏因子進(jìn)行區(qū)分,從而確定各數(shù)據(jù)對(duì)象的子空間定義向量,得到數(shù)據(jù)對(duì)象對(duì)應(yīng)的相關(guān)子空間,解決了檢測(cè)相關(guān)子空間時(shí),時(shí)間復(fù)雜度較高的問題,一定程度上提高了算法的效率,但是,由于得到相關(guān)子空間時(shí),是通過同一個(gè)閾值對(duì)所有的維度確定子空間,當(dāng)各個(gè)維度的數(shù)據(jù)分布有差異時(shí),得到的相關(guān)子空間有一定的誤差.

綜上所述,當(dāng)數(shù)據(jù)對(duì)象分布不一致時(shí),在檢測(cè)到的相關(guān)子空間中,離群程度的度量不明顯;在確定相關(guān)子空間時(shí),具有維度指數(shù)級(jí)的時(shí)間復(fù)雜性;當(dāng)參數(shù)閾值選擇不合適的時(shí)候,精度無法保證,限制了算法的適用性.因此,其挖掘的效率和準(zhǔn)確性也無法得到保證.

3 基本概念

在數(shù)據(jù)集中,分布集中或密度差異小的子空間稱之為稠密子空間,分布稀疏或密度差異大的子空間稱之為稀疏子空間.離群數(shù)據(jù)與正常數(shù)據(jù)的密度存在差異,離群數(shù)據(jù)是密度差異比較大的數(shù)據(jù)對(duì)象,密度差異較大的子空間,即稀疏子空間中包含有出比較多的對(duì)離群數(shù)據(jù)有價(jià)值的信息,而密度差異比較小的子空間,即稠密子空間中對(duì)離群數(shù)據(jù)有價(jià)值的信息比較少,因此將能體現(xiàn)更多對(duì)離群數(shù)據(jù)有價(jià)值信息的稀疏子空間稱之為相關(guān)子空間,將體現(xiàn)較少對(duì)離群數(shù)據(jù)有價(jià)值信息的稠密子空間稱之為不相關(guān)子空間.

在文獻(xiàn)[9]中,為了尋找對(duì)離群數(shù)據(jù)有價(jià)值信息的稀疏子空間,利用數(shù)據(jù)對(duì)象的局部數(shù)據(jù)集LDS來計(jì)算第i條數(shù)據(jù)第j維度的數(shù)據(jù)稀疏度:

(1)

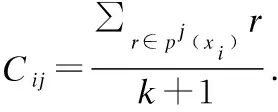
由公式(1)可知,yij是局部數(shù)據(jù)各屬性維的方差,yij較大,表明xij在其局部數(shù)據(jù)集中的密度較小,xij所在的是稀疏子空間;反之,yij較小,表明xij在其局部數(shù)據(jù)集中的密度較大,xij所在的是稠密子空間.

稀疏度的引入,是可以更方便衡量數(shù)據(jù)空間的稠密和稀疏區(qū)域,發(fā)現(xiàn)數(shù)據(jù)空間的相關(guān)子空間.COAS算法[9]中使用局部稀疏差異因子閾值,來判斷數(shù)據(jù)的相關(guān)子空間,但是,由于每個(gè)維度的數(shù)據(jù)分布特征不一致,這樣會(huì)導(dǎo)致確定的相關(guān)子空間不準(zhǔn)確.

4 相關(guān)子空間和離群值

4.1 相關(guān)子空間

依據(jù)文獻(xiàn)[21],如果子空間S是稀疏子空間,則S是相關(guān)子空間;如果子空間S是稠密子空間,則S是不相關(guān)子空間.因此,可以通過識(shí)別子空間S中每個(gè)維度的稠密子空間和稀疏子空間,來確定出相關(guān)子空間.稀疏度矩陣每個(gè)維度的稀疏度yij是由稀疏子空間和稠密子空間混合組成的,而高斯混合模型的靈活性使其能夠很好地適應(yīng)稀疏度的分布,因此,通過高斯混合模型和EM算法識(shí)別稀疏度yij所在的子空間,可以得到該維度的稀疏子空間和稠密子空間,將其稀疏子空間視為相關(guān)子空間.

把一維數(shù)據(jù)對(duì)象xi稀疏度yij用作高斯混合模型:

(2)

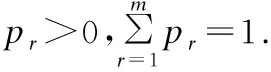
第r個(gè)高斯分布的密度函數(shù)為:

(3)

其中:每個(gè)部分的Nr含有兩個(gè)參數(shù)期望μr和標(biāo)準(zhǔn)差σr,μr是高斯分布的位置參數(shù),描述正態(tài)分布的集中趨勢(shì)位置,分布以μr為對(duì)稱軸,左右完全對(duì)稱.σr描述正態(tài)分布資料數(shù)據(jù)分布的離散程度,σr越大,數(shù)據(jù)分布越分散,σr越小,數(shù)據(jù)分布越集中,σr也稱為是正態(tài)分布的形狀參數(shù),σr越大,曲線越扁平,反之,σr越小,曲線越瘦高.

使用高斯混合模型對(duì)每一維度稀疏度進(jìn)行擬合,把稀疏度分為兩個(gè)高斯分布,稀疏度較大的分布中的數(shù)據(jù)構(gòu)成相關(guān)子空間,較小的分布中的數(shù)據(jù)構(gòu)成無關(guān)子空間,因此該高斯混合模型由兩個(gè)高斯分布組成,即m=2.

使用EM算法來估計(jì)高斯混合模型各個(gè)參數(shù)[10],算法思想為:1)初始化:r1=r2=0,σ1=σ2=1,μ1、μ2為隨機(jī)數(shù);2)E步,計(jì)算后驗(yàn)概率;3)M步,根據(jù)后驗(yàn)概率計(jì)算新的r1、r2、μ1、μ2、σ1、σ2;4)判斷是否結(jié)束,如果沒有,返回2).

通過EM算法便可以得到每一維度的每個(gè)稀疏度屬于兩個(gè)高斯分布的概率值pi1和pi2,即可得到每一維度的每個(gè)數(shù)據(jù)對(duì)象稀疏度的高斯分布種類:當(dāng)pi1>pi2時(shí),該稀疏度屬于第一個(gè)高斯分布;否則屬于第二個(gè)高斯分布.同時(shí)可以得到每一維度的兩個(gè)高斯分布的均值μ1、μ2,當(dāng)μ1>μ2時(shí),第一個(gè)高斯分布的稀疏度比較大,構(gòu)成的子空間是稀疏子空間,第二個(gè)高斯分布的稀疏度比較小,構(gòu)成的區(qū)域是稠密子空間,否則,相反.

定義:對(duì)于數(shù)據(jù)對(duì)象xi,yij是第i個(gè)數(shù)據(jù)對(duì)象第j維度的稀疏度,zi是其子空間向量,zij是第i個(gè)數(shù)據(jù)對(duì)象第j維度的值,如果yij屬于稀疏子空間,則zij=1,如果yij屬于稠密稠密子空間,則zij=0.在zi中,由值為1的屬性維組成的空間稱之為第i個(gè)數(shù)據(jù)的相關(guān)子空間,由值為0的屬性維組成的空間稱之為第i個(gè)數(shù)據(jù)的不相關(guān)子空間.

因此,利用稀疏度和上面的定義可以得到數(shù)據(jù)集各個(gè)數(shù)據(jù)對(duì)象的子空間向量.

COAS算法中子空間是根據(jù)其局部數(shù)據(jù)集是否均勻來判斷的,而在實(shí)際數(shù)據(jù)中均勻分布是極為罕見的,因此采用均勻分布來判斷相關(guān)子空間有一定的局限性.同時(shí),在選擇閾值時(shí),COAS算法在不同維度選擇同一個(gè)閾值進(jìn)行相關(guān)子空間向量的計(jì)算,而在實(shí)際情況中每個(gè)維度的數(shù)據(jù)分布情況不完全相同.本算法避免用戶設(shè)置的閾值參數(shù),采用的混合高斯分布的方法可以自適應(yīng)地識(shí)別每個(gè)維度的相關(guān)子空間.

4.2 離群值

根據(jù)相關(guān)子空間的定義,可以得到第i個(gè)數(shù)據(jù)對(duì)象的相關(guān)子空間,而稀疏度可以表示子空間的密度,離群程度越高,稀疏度越大,子空間的密度越小.因此,在相關(guān)子空間中,利用數(shù)據(jù)對(duì)象每個(gè)維度的稀疏度和每個(gè)維度的權(quán)值,可以有效地衡量數(shù)據(jù)對(duì)象的離群程度.

參照文獻(xiàn)[8],數(shù)據(jù)對(duì)象i的離群值定義為:

(4)

即每個(gè)數(shù)據(jù)對(duì)象的離群值是該對(duì)象每個(gè)維度的離群程度之和,數(shù)據(jù)對(duì)象的離群值越高,其離群程度越大.數(shù)據(jù)對(duì)象i第j維的離群程度為:

(5)

其中,wj是每個(gè)維度在整個(gè)維度中的權(quán)值.

(6)

COAS算法中離群分?jǐn)?shù)是把每個(gè)維度同等看待,并沒有考慮到每個(gè)維度在數(shù)據(jù)空間中的重要性,本算法加入了權(quán)值因子能準(zhǔn)確地區(qū)分每個(gè)數(shù)據(jù)對(duì)象的離群值.

5 RSGMM算法描述

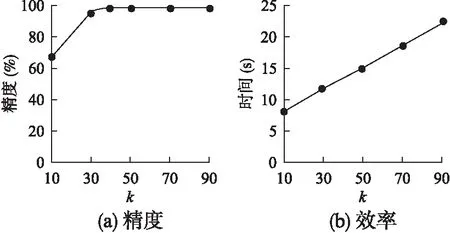
利用高斯混合分布模型確定相關(guān)子空間,并計(jì)算數(shù)據(jù)對(duì)象的離群值基本步驟:首先,生成數(shù)據(jù)集中每個(gè)數(shù)據(jù)對(duì)象的局部數(shù)據(jù)集LDS,然后根據(jù)公式(1)計(jì)算每個(gè)數(shù)據(jù)對(duì)象的稀疏度,生成全局地稀疏度矩陣;其次,利用混合分布和EM算法,確定每個(gè)數(shù)據(jù)對(duì)象的相關(guān)子空間;然后利用得到的相關(guān)子空間,根據(jù)公式(4)、(5)和(6)計(jì)算每個(gè)數(shù)據(jù)對(duì)象的離群值;最后選取離群值最高的若干個(gè)各數(shù)據(jù)對(duì)象,并將其視為離群數(shù)據(jù).具體算法如下:

算法1.RSGMM算法

輸入:數(shù)據(jù)集DS

輸出:離群數(shù)據(jù)

1)n=數(shù)據(jù)集DS的數(shù)據(jù)個(gè)數(shù),d=數(shù)據(jù)集DS的維度;

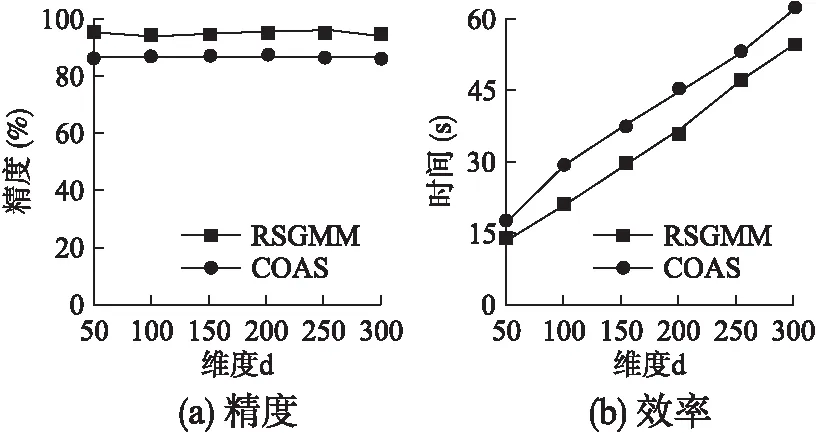
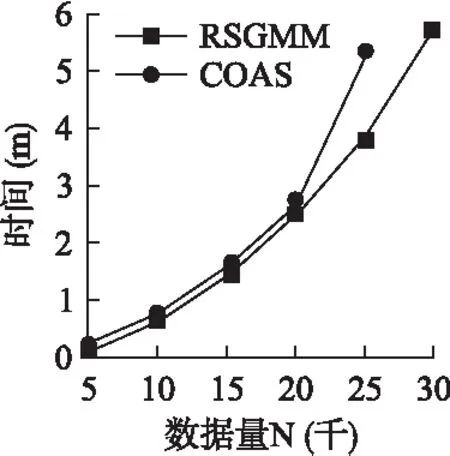
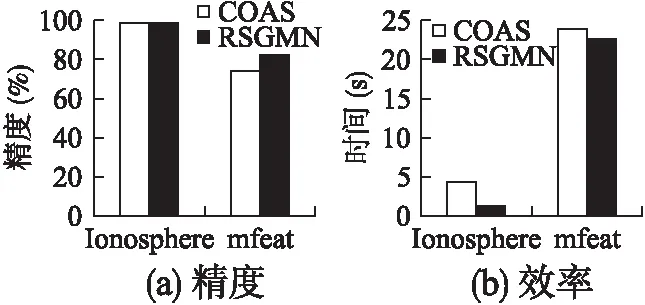
2)for(i=0;i

3)LDSi=getknn();//計(jì)算第i個(gè)數(shù)據(jù)對(duì)象的局部數(shù)據(jù)集LDS

4)spi=getspdegree();//計(jì)算第i個(gè)數(shù)據(jù)對(duì)象的稀疏度

5)}

6)Z=getsubspace();//計(jì)算相關(guān)子空間

7)for(i=0;i

8)Ri=getscore();//計(jì)算第i個(gè)數(shù)據(jù)對(duì)象的離群值

9)}

10)返回離群值最大的N個(gè)對(duì)象;

算法2.getspdegree()

輸入:數(shù)據(jù)集DS,第i條數(shù)據(jù)對(duì)象的局部數(shù)據(jù)集LDS

輸出:第i條數(shù)據(jù)對(duì)象的稀疏度

1)for(j=0;j

2)for(m=0;m

3)ine=line+LDS[m][d];

4)}

5)pij=getsp(line);//根據(jù)公式(1)計(jì)算稀疏度

6)}

算法3.getsubspace()

輸入:稀疏度矩陣sp

輸出:二進(jìn)制矩陣Z

1)for(j=0;j

2)根據(jù)EM思想進(jìn)行迭代,得到Pik(k=0,1);//Pi為數(shù)據(jù)對(duì)象第j維屬性屬于第k類的概率

3)選擇概率較大的類作為該屬性的類別k(k=0,1);

4)for(i=0;i

5)選擇均值較大的類別m(m=0,1);

6)if(m==k)

7)Zij=1;

8)else

9)Zij=0;

10)}}

算法4.getscore()

輸入:稀疏度矩陣sp,二進(jìn)制矩陣Z

輸出:第i個(gè)數(shù)據(jù)對(duì)象的離群值Ri

1)for(j=1;j<=d;j++){

2)根據(jù)公式(6)計(jì)算wj;//計(jì)算每個(gè)屬性的權(quán)值

3)}

4)for(j=1;j<=d;j++){

5)根據(jù)公式(4)計(jì)算離群值Ri;//計(jì)算第i 個(gè)數(shù)據(jù)對(duì)象的離群值Ri

6)}

RSGMM算法中,計(jì)算各數(shù)據(jù)對(duì)象的局部數(shù)據(jù)集時(shí),時(shí)間復(fù)雜度為O(n*logn),求每個(gè)數(shù)據(jù)對(duì)象求各屬性的局部稀疏因子,生成原數(shù)據(jù)的稀疏因子矩陣時(shí),其時(shí)間復(fù)雜度為O(n*k*d),識(shí)別相關(guān)子空間和確定離群值部分的時(shí)間復(fù)雜度是O(n*d)+O(d*t)+O(n*d)≈O(n*d),因此,RSGMM算法的時(shí)間復(fù)雜度是O(n*logn)+O(n*k*d)+ O(n*d).

6 實(shí)驗(yàn)結(jié)果及分析

實(shí)驗(yàn)環(huán)境:Intel(R)Core(TM)i5-3470CPU,2GB內(nèi)存,windoes 7操作系統(tǒng),eclipse 作為開發(fā)平臺(tái),采用 Java 語言實(shí)現(xiàn)了RSGMM算法.

6.1 人工數(shù)據(jù)集

生成50維、100維、150維、200維、250維和300維的5000條人工數(shù)據(jù)集;生成了50維的5000條、10000條、15000條、20000條、25000條和30000條人工數(shù)據(jù)集.在每條人工數(shù)據(jù)集中有3%的數(shù)據(jù)是離群數(shù)據(jù),其中,正常數(shù)據(jù)由N(0,1)的正態(tài)分布生成的隨機(jī)數(shù),離群數(shù)據(jù)是由N(1,1)的正態(tài)分布生成的隨機(jī)數(shù).

1)參數(shù)k對(duì)RSGMM算法精度和效率的影響

采用數(shù)據(jù)量為5000條,維度為50維的人工數(shù)據(jù)集,對(duì)不同的k進(jìn)行實(shí)驗(yàn),實(shí)驗(yàn)結(jié)果如圖1所示.

圖1 k值對(duì)算法精度和效率的影響

由圖1(a)可知,隨著k值得增加,RSGMM算法的挖掘精度也將提高,主要原因是k值增大時(shí),數(shù)據(jù)對(duì)象的局部數(shù)據(jù)集增多,使得數(shù)據(jù)對(duì)象的稀疏度增大,但是離群數(shù)據(jù)的稀疏度增大的幅度比正常數(shù)據(jù)明顯,利用混合概率模型劃分時(shí),離群數(shù)據(jù)的所在的稀疏區(qū)域能更明顯地識(shí)別出來,得到的相關(guān)子空間更加準(zhǔn)確,其挖掘精度更高;當(dāng)k>40時(shí),算法的挖掘精度基本保持不變,其主要原因是:k值達(dá)到一定值時(shí),數(shù)據(jù)的局部數(shù)據(jù)集可以體現(xiàn)其特征結(jié)構(gòu). 由圖1(b)可知,近鄰個(gè)數(shù)k對(duì)算法的挖掘效率影響比較大.隨著k值得增大,其挖掘效率降低,主要原因是RSGMM算法大約70%多的時(shí)間用來計(jì)算稀疏度,且計(jì)算稀疏度時(shí)需要尋找k近鄰,k值的越大,尋找k個(gè)最近鄰的計(jì)算量也會(huì)隨之增多.

2)維度對(duì)挖掘精度、效率的影響

采用數(shù)據(jù)量為5000條,維度分別為50維、100維、150維、200維、250維和300維的人工數(shù)據(jù)集,在參數(shù)k=40時(shí)對(duì)不同的維度進(jìn)行實(shí)驗(yàn),實(shí)驗(yàn)結(jié)果如圖2所示.

圖2 維度對(duì)算法的影響

在圖2(a)中,維度對(duì)該RSGMM算法和COAS算法的挖掘精度都影響較低,其挖掘精度基本保持不變,主要是RSGMM算法在計(jì)算離群值前,首先進(jìn)行了相關(guān)子空間的識(shí)別,排除了無關(guān)子空間對(duì)挖掘精度的影響,維度變化,對(duì)相關(guān)子空間維度影響不是太大.

但是,COAS算法比RSGMM算法的挖掘精度低,主要原因:1)在識(shí)別子空間的時(shí)候,COAS采用的是同一個(gè)閾值對(duì)所有維度進(jìn)行區(qū)分,而在實(shí)際情況中每個(gè)維度的數(shù)據(jù)分布情況不完全相同,RSGMM算法采用混合分布的方法自適應(yīng)對(duì)每個(gè)維度的數(shù)據(jù)進(jìn)行區(qū)分,得到的相關(guān)子空間準(zhǔn)確率比較高;2)COAS算法中離群分?jǐn)?shù)是把每個(gè)維度同等看待,并沒有考慮到每個(gè)維度在數(shù)據(jù)空間中的重要性,RSGMM算法加入了權(quán)值因子,能更好地區(qū)分每個(gè)數(shù)據(jù)的離群值.

在圖2(b)中,RSGMM算法和COAS算法耗時(shí)隨著維度的增加而線性增加,主要原因:1)RSGMM算法中,與維度相關(guān)的步驟稀疏度計(jì)算(公式(1))、確定相關(guān)子空間識(shí)和離群分?jǐn)?shù)時(shí)的計(jì)算(公式(3)和(4)),都與維度是線性關(guān)系;2)COAS算法中,計(jì)算稀疏因子、稀疏差異因子、離群因子時(shí),計(jì)算量都與維度d呈線性關(guān)系.

但是,RSGMM算法耗時(shí)比COAS算法要少,與圖1的原因一致,RSGMM算法比COAS算法得到的相關(guān)子空間更加準(zhǔn)確,得到的相關(guān)子空間維度更小,使得RSGMM算法在相關(guān)子空間中離群因子的計(jì)算量更小,算法消耗的時(shí)間更少.

3)數(shù)據(jù)量對(duì)算法挖掘效率的影響

圖3 數(shù)據(jù)量對(duì)算法效率的影響

采用數(shù)據(jù)量分別為5000條、10000條、15000條、20000條、25000條和30000條,維度為50維的人工數(shù)據(jù)集,在參數(shù)k=40時(shí)對(duì)不同的數(shù)據(jù)量進(jìn)行實(shí)驗(yàn),實(shí)驗(yàn)結(jié)果如圖3所示.圖3中,RSGMM算法和COAS算法所消耗的時(shí)間都隨著數(shù)據(jù)量的增加而增加,主要是由于隨著數(shù)據(jù)量的增加,計(jì)算每個(gè)數(shù)據(jù)數(shù)據(jù)KNN、稀疏度、離群值的時(shí)間也會(huì)隨著增加.

RSGMM算法比COAS算法所消耗的時(shí)間少,原因與圖2一樣,RSGMM算法得到的相關(guān)子空間維度比較小,使得在較小維度的相關(guān)子空間中計(jì)算離群因子時(shí),所消耗的時(shí)間大大降低,并且數(shù)據(jù)量越大,時(shí)間差距也越大,當(dāng)數(shù)據(jù)量大于30000時(shí),執(zhí)行COAS算法所需要的內(nèi)存超出了計(jì)算機(jī)的承受范圍.

6.2 UCI數(shù)據(jù)集

使用UCI數(shù)據(jù)集Ionosphere和mfeat,實(shí)驗(yàn)驗(yàn)證算法的精度和效率,表1為UCI數(shù)據(jù)集的組成.

表1 UCI數(shù)據(jù)集

在圖4(a)中,數(shù)據(jù)集Ionosphere中,RSGMM算法和COAS算法的精度都是100%.數(shù)據(jù)集mfeat中,RSGMM算法比COAS算法中的精度要高,這是由于COAS算法得到相關(guān)子空間的是依據(jù)數(shù)據(jù)對(duì)象在其局部數(shù)據(jù)集中分布是否均勻來判斷的,均勻分布的要求比較嚴(yán)格,得到的相關(guān)子空間包含了一些不相關(guān)的維度,隱藏在不相關(guān)的維度中的有些離群數(shù)據(jù)無法找到,而RSGMM算法可以發(fā)現(xiàn)影響大部分隱藏?cái)?shù)據(jù)的相關(guān)子空間.

圖4 UCI數(shù)據(jù)集對(duì)算法效率的影響

圖4(b)中,在數(shù)據(jù)集Ionosphere和mfeat中,RSGMM算法比COAS算法消耗的時(shí)間要少,主要原因是RSGMM算法得到的相關(guān)子空間維度更小,使得在相關(guān)子空間中計(jì)算離群值時(shí),消耗的時(shí)間更少.

7 結(jié)束語

本文針對(duì)高維離群數(shù)據(jù),給出了一種基于相關(guān)子空間的離群數(shù)據(jù)挖掘算法.該算法利用各個(gè)數(shù)據(jù)對(duì)象各屬性維的稀疏度(可以體現(xiàn)數(shù)據(jù)的稠密與稀疏)和高斯混合分布,確定各個(gè)數(shù)據(jù)對(duì)象的相關(guān)子空間和不相關(guān)子空間,有效地避免不相關(guān)子空間對(duì)挖掘精度和效率的影響;在相關(guān)子空間中,利用各個(gè)數(shù)據(jù)的稀疏度和各個(gè)屬性維的權(quán)值來度量數(shù)據(jù)對(duì)象離群值,可以準(zhǔn)確地度量數(shù)據(jù)對(duì)象的離群值;然后,將離群值最大的若干個(gè)數(shù)據(jù)對(duì)象視為離群數(shù)據(jù);最后,采用人工數(shù)據(jù)集和UCI數(shù)據(jù)集實(shí)驗(yàn)驗(yàn)證了該算法正確性和有效性.下一步的工作是算法的并行化,以適應(yīng)于海量高維數(shù)據(jù).