基于圖正則化和l1/2稀疏約束的非負矩陣分解算法
張 旭,陳志奎,高 靜
(大連理工大學 軟件學院,遼寧 大連 116620)
1 引 言
隨著計算機科學的發展,傳統的數據挖掘與機器學習方法得以橫跨多個學科,在諸多領域得到重要的應用.例如,醫學疾病的診療和生物學研究過程中,組織細胞的基因表達譜能夠以高維數據的形式導出,這為應用數據挖掘手段對其進行進一步分析和處理提供了可能.然而受限于現有獲取方式,所有檢測到的基因全部被導出,實際起表達作用的基因可能在其中只占小部分.這導致得到的基因譜數據集往往規模龐大、形式復雜,維度遠大于樣本實例數;同時包含大量冗余,傳統數據挖掘算法難以發揮其性能.
為解決該問題,對原始基因表達譜數據進行維數約簡[1]是最行之有效的方法之一.該方法通過對原始數據空間進行數學投影變換以獲得新的特征空間.較之原始空間,該空間維度大幅精簡,概括能力更強,因而可以更好地描述基因數據.而基因數據通常以矩陣形式進行存儲,對大規模數據的處理可直觀理解為高維矩陣的分析,這就為使用矩陣分解方法進行維度約簡提供了條件.傳統含負分解方法由于分解結果中的負元素缺乏直觀的物理意義[2],在實際應用中有著很大局限性.另一方面,因為基因樣本規模龐大,且樣本之間存在相互聯系,線性變換的過程中可能會破壞基因譜數據的內部結構.故此,基于非負矩陣分解思想的方法由于實現了原始矩陣維數的非線性約減,且通過非負約束保證了分解后元素的物理意義,甫一提出便得到了廣大研究人員的重視.1999年,Lee和Seung在前人研究基礎上進行總結歸納,于《Nature》上首次正式提出非負矩陣分解方法(Non-negative matrix factorization,NMF)[2]的概念,并證明了其收斂性,為矩陣分解問題開辟了新的思路.其后的十幾年里,非負矩陣分解研究方興未艾,廣大學者紛紛將NMF方法進行推廣和改進.時至今日,NMF已被廣泛應用到基因及細胞分析領域的研究中[3].并逐漸成為最受歡迎的多維數據處理工具之一.NMF在維數約簡上有著得天獨厚的優勢:通過結合流形學習,能夠較為完整地保持數據原有的內部空間結構;添加稀疏約束后,也可以較好地抑制噪聲.迄今為止,已有很多學者將稀疏的判別信息與流形思想相結合,對NMF算法進行改進[4,5].
流形學習(Manifold Learning)是近年來流行的機器學習方法.流形思想將高維數據映射至低維空間以揭示數據的本質結構,在維數約簡上得到廣泛應用[6].Cai等人將該思想引入,提出圖正則化非負矩陣分解(Graph Regularized nonnegative matrix factorization,GRNMF)[7],并在之后通過一系列研究對其應用方式進行拓展,進一步提升了非負矩陣分解保存原始數據局部特征的能力[8].
非負約束使得基于非負矩陣分解的方法其結果天然具有一定程度的稀疏性.從數據角度這意味著分解得到的矩陣中將包含很多0元素.NMF在稀疏性的作用下,得以使用更少元素表示原有數據,節省存儲空間,為數據表達提供一種高效的策略[9].在實際應用中,這種天然的稀疏性往往不夠充分,基于實際需求,研究人員常結合稀疏表示理論,在目標函數中引入稀疏性約束,以合理控制NMF結果的稀疏程度,達到更優的分解效果,使結果更具實際應用意義.稀疏編碼思想與NMF相結合的方法由Hoyer在2002年首先提出,該方法利用歐氏距離的平方加上l1范數,得到一種非負稀疏編碼(Nonnegative sparse coding,NNSC)算法,并通過實驗證明了其分解結果在稀疏程度上的優勢[10].隨后Hoyer對NNSC算法作了進一步改良,利用非線性投影實現對稀疏性的精確控制,給出一種介于l1范數和l2范數之間的稀疏度計算準則并提供相應軟件包,極大地促進了稀疏約束NMF研究和應用的發展[9].
通常使用的l1約束在分解含噪聲數據時,稀疏表示的有效性受到干預,結果可能仍含有較多噪聲,影響降噪效果[11].徐宗本等人針對l1稀疏性問題提出了更加稀疏的l1/2正則理論,并對求解算法和收斂性進行了分析[11].很多學者也對lq范數約束在q取不同值時對NMF算法稀疏性的影響進行研究,驗證了l1/2約束在稀疏性表示上的優勢[12].近年來,已有更多算法使用了l1/2約束的思想[13,14].
綜上所述,針對基因表達譜數據高維度、高冗余的特點,本文提出了一種基于非負矩陣分解的算法,結合圖正則化思想和使用l1/2范數的稀疏約束,進一步加入了去噪處理,對NMF算法進行改進,使之得以更好地應用于腫瘤基因表達譜數據的維度約簡工作中.實驗表明,相較傳統方法,該算法在處理含有大量冗余的腫瘤基因表達譜數據時更加有效.
2 非負矩陣分解理論
NMF的基本思想是任意給定一個高維非負矩陣X,可以找到兩個低維的非負矩陣W和H,使得W與H的乘積近似地逼近原始矩陣,從而將原矩陣分解成兩個非負矩陣的乘積.其數學模型為:
X≈WH
(1)
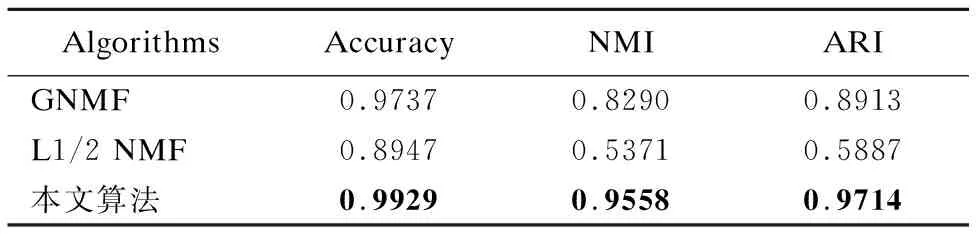
若原始矩陣X是L×P的矩陣,則W為L×N階矩陣,H為N×P階矩陣,其中N (2) 在基本的NMF目標函數加上范數約束的方法不僅表示簡單,易于理解,而且可以根據具體情況對不同變量附加稀疏性限制,從而得到期望的性質.此外,圖正則化方法,噪聲處理等方法和演化,都可以通過不同方式被添加到目標函數中.為了將稀疏編碼理論與NMF算法相結合,通常對分解后的系數矩陣H進行稀疏約束.稀疏約束的選擇一般采用范數約束的方法,常用的包括l1范數和l2范數[9,16],lp范數(0≤p<1)約束在p等于1/2的時候目前被認為是一種行之有效的方法[14]. 使用傳統NMF及其衍生算法進行基因表達譜數據集的維度約簡工作時,由于原始數據維度較高且含有大量冗余和噪聲數據,在沒有進行對應處理的情況下,算法性能難以發揮,效果并不夠盡如人意.針對基因表達譜數據高維度、高冗余的特點,本文基于非負矩陣分解方法的思想,結合圖正則化思想和稀疏性約束,進一步加入去噪處理,對NMF算法進行改進,提出的算法對處理過度冗余的高維基因表達譜數據特別有效.此外,區別于傳統稀疏算法中使用的l1范數約束,我們選擇l1/2范數進行稀疏性約束,進一步提升了算法的性能. 為了引入噪聲項的定義,我們將原始數學模型定義為: X=WH+E (3) 之后為了得到最優解,目標函數定義為: (4) 其中λα是調整稀疏程度的參數;λβ∈R+是一個標量,用于調整流形約束的權重.λγ是控制降噪的參數.Tr(·)是矩陣的跡.L是一個拉普拉斯(Laplacian)矩陣,可以由圖權重矩陣G和對角矩陣D由以下公式計算得到: L=D-G (5) 對于給定的兩個實例yi和yj,使用高斯核度量計算實例間的相似度,從而得到權重矩陣G: (6) 之后可以計算對角矩陣D: Dii=∑i=1Gij (7) 對目標函數的優化過程等價于如下公式的最小化問題. (8) 可以使用迭代更新的辦法解決.基本思路是固定其他變量,對W,H,E分別進行更新.具體的更新優化過程如下: 3.2.1 更新E 首先我們需要證明噪聲項的引入不會影響分解過程中非負性的保持,以便采用非負矩陣分解的經典思想對該問題進行優化求解.當固定W,H時,對E的更新優化問題變為: (9) 這是一個帶l1范數約束的最小化問題,可以通過軟閾值操作符的方式進行求解.其更新規則如下: (10) 通過該更新規則可以保證X-E≥0.證明如下: 綜上,在上述更新規則下,可以保證X-E≥0. 通過證明,我們可以保證加入去噪處理后矩陣元素的非負性.由此我們在接下來的工作中,就可以利用一般非負矩陣分解的方法來進行對W,H的迭代更新. 3.2.2 更新W 為了方便說明,因為我們已經證明了X-E≥0,我們令Z=X-E. 當固定H,E時,對W的更新優化問題變為: (11) 由于我們已經知道Z非負,則該優化問題屬于一個非負二次規劃問題,和傳統非負矩陣分解模型類似,可以參考傳統非負矩陣分解模型的迭代更新規則[16]進行處理.相應的,我們得到用于迭代更新W的更新規則如下: (12) 3.2.3 更新H 固定W,E時,對H的更新優化問題變為: (13) H可以看作是實例在低維空間中的表示,圖正則化思想為了在低維空間保持實例的原始結構,需要用下面的式子對低維表示的平滑性進行度量: (14) 對R進行變換,可得: =Tr(HLHT) (15) 因此在對H進行更新時,需要考慮正則化項Tr(HLHT).參照Cai提出的圖正則化優化理論[8],我們使用梯度下降的方法對H進行優化: 設更新H的目標函數為O,有如下的加法更新規則: (16) 其中δi,j是步長參數. 令δi,j=-hi,j/2(WTWH+λβHDT)i,j,可得: (17) 對于l1/2稀疏約束項,我們參照已有的添加稀疏約束的方法[13]. 綜上,我們可以得到用于迭代更新H的更新規則如下: (18) 本節結合前文對算法模型和優化過程的介紹,給出本文提出算法過程的簡要描述(見表1). 我們使用兩個取自真實采樣的常用基因數據集,ALL-AML和Colon[17],用于衡量算法的性能.ALL-AML數據集包含38個實例的5000個基因,包括27個ALL細胞和11個AML細胞.Colon數據集中包含62條實例,表示62個組織的2000個基因,其中40個組織是腫瘤,另外22個活檢是從同一患者健康的組織部分收集而來. 該理論已經得到證明:當維度約簡處理后的維度等于實際類標簽數量時,后續聚類中得到的結果無論從開銷和性能上都相對優秀[18].因此我們選擇聚類領域常用的評價標準,包括正確率(Accuracy,ACC)、標準互信息(Normalized Mutual Information,NMI)和蘭德指數(Adjusted Rand Index,ARI[19])進行評估.它們的取值范圍都在[0,1]之間.ACC用于描述點和簇的一一對應關系,其原理是使聚類的結果和真實的結果盡可能匹配,ACC越大,代表聚類的效果越好.令qi為數據實例xi使用聚類算法得到的簇標簽,pi為數據實例xi的真實簇標簽,則ACC定義如下: (19) NMI[20]基于互信息的方法來衡量聚類效果,需要實際類別信息.它代表當一個類的信息已知的時候,對推測出關于另一個類的信息有多少幫助.若兩個類沒有共同的信息,即互信息為0.值越大意味著聚類結果與真實情況越吻合.令算法得到的聚類結果為C,給定聚類標簽為R,H是來自聚類集合的熵信息,可以得到NMI的定義. (20) 表1 算法描述 類似的,ARI的計算方式可以由如下公式定義: (21) 在對比算法的選擇方面,由于我們的算法結合了這兩類算法的思想,我們選擇GNMF[11]和l1/2NMF[8]進行對比.GNMF是圖正則化的基本非負矩陣分解方法,通過在分解過程中添加幾何分布信息提高算法性能;l1/2NMF對分解后的系數矩陣添加l1/2范數的稀疏約束. 實驗中我們隨機產生數據集實例的輸入順序,進行多組實驗,并在每組內進行多次重復實驗.為了公平地對比算法在理想情況下可能表現的最佳性能,對于所有的算法,我們都使用并記錄它們的參數為最優值時,所能得到的最好結果.算法需要提供維度約簡處理后產生的新的特征空間的維度,該維度設置為與實際類標簽數目相同.維度約簡完成后,使用k-means算法進行聚類,并與實際類標簽進行比對,以衡量算法性能.實驗結果如表2和表3所示. 表2 ALL-AML數據集上的平均結果 表3 Colon數據集上的平均結果 圖1 算法在ALL-AML數據集上的對比結果 圖2 算法在Colon數據集上的對比結果 可以看出,我們的算法應用于腫瘤細胞基因數據集時,在準確率和可區分度上,相較已有算法都存在顯著的優勢. 本文提出了一種基于非負矩陣分解思想,結合圖正則化理論和l1/2范數稀疏約束的算法,該方法可以用于對細胞基因表達譜數據進行維度約簡.算法結合了已有工作的優勢,在保證對數據局部和全局結構的描述能力和對稀疏性的約束能力基礎上,針對基因表達譜數據經常存在過度冗余的問題,通過引入去噪處理,大幅提高了算法性能.實驗結果證明,算法在基因數據聚類上的表現整體優于傳統基于非負矩陣分解的算法. 在使用稀疏約束的NMF方法中,控制稀疏度的參數(本文為λα)大多根據實驗經驗得來.如何通過理論上的推導和證明,從而合理控制參數以達到最優效果,將是未來一個有價值的研究思路.
3 本文提出的算法
3.1 算法基本模型

3.2 優化過程
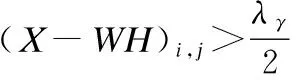


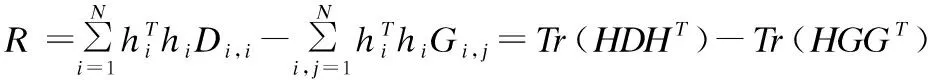

3.3 算法描述
4 實 驗
4.1 數據集
4.2 評估指標
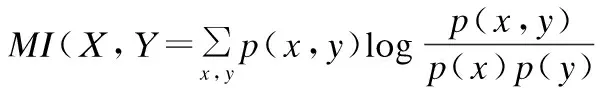




5 結論和展望

