基于局部自動編碼器的手寫數字分類
盧海峰,衛 偉,陸慧娟
(中國計量大學 信息工程學院,杭州 310018)
1 引 言
黃廣斌等在2006年提出的超限學習機(Extreme Learning Machine,ELM)在分類和回歸問題上具有泛化性能好、分類精度高、訓練速度快等優點[1].然而隨機初始化的特性正是其缺點所在[2],即輸入權值和閾值的隨機初始化導致了模型性能的不穩定性.文獻[3]將受限玻爾茲曼機與ELM將結合,在對數據降維的同時,得到了ELM的輸入權值和閾值.文獻[4,5]分析了初始化不同的參數對ELM性能的影響:文獻[4]針對輸入權值的不同分布進行了研究,文獻[5]針對輸入權值和閾值的方差進行了研究.當訓練樣本參與到輸入權值的初始化過程時,ELM分類精度得到了明顯的提高[6,7],但它們都只是簡單地組合訓練樣本,并沒有充分提取和表達訓練樣本集的特征.文獻[8]將訓練樣本先經過自動編碼器(auto-encoder,AE),再將其輸出權值用于ELM輸入權值的初始化,并提出了基于AE逐層提取特征的方法.文獻[9]提出了類限制超限學習機(class-constrained extreme learning machine,C2ELM),算法將訓練數據按類通過AE進行訓練,大大降低了計算過程中的使用內存,在一定程度上也提高了分類精度.輸入權值的稀疏性可以進一步提高模型的性能,文獻[10]將圖像的局部區域作為輸入權值的初始化,提出了局部感知的ELM.本文從文獻[9,10]得到靈感,首先結合權值的稀疏性和分類訓練的方法提出了基于局部自動編碼器(local auto-encoders,LAE)的類限制超限學習機(receptive field class-constrained extreme learning machine,RF-C2ELM),然后比較ELM-AE(Extreme Learning Machine Auto Encoder)、C2ELM和RF-C2ELM在不同隱層結點數下的訓練時間,接著將C2ELM和RF-C2ELM擴展為多層神經網絡,并與ML-ELM(Multi Layer Extreme Learning Machine)作比較.
2 相關知識
2.1 ELM
對于任意N個互不相同的訓練樣本與對應標簽的集合,數據組織形式為(xi,ti),其中xi=[xi1,xi2,…,xin]T∈Rn是模型的輸入,ti=[ti1,ti2,…,tim]T∈Rm是整個模型的期望輸出,i=1,2,…,N.假設SLFNs(Single-hidden layer feedforward neural networks)具有K個隱層結點,模型可以表示成:
(1)
其中oi=[oi1,oi2,…,oim]T∈Rm為模型的實際輸出,ωi=[ωi1,ωi2,…,ωiK]T∈RK為連接輸入層和隱層的權值向量,βi=[βi1,βi2,…,βim]T∈Rm為連接隱層和輸出層的權值向量,bi為第i個隱層結點的閾值,f(·)為隱層的激活函數,通常選擇sigmoid函數作為激活函數,ωi·xj表示ωi和xj的內積.如果具有K個隱層結點的SLFNs能以零誤差逼近樣本,(1)式可以簡化成:
Hβ=T
(2)
其中
(3)
于是有:
(4)
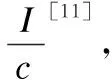
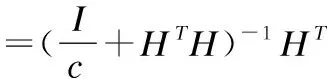
(5)
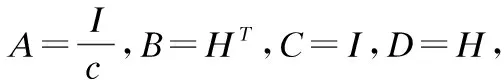
(A+BCD)-1=A-1B(C-1+DA-1B-1)-1
(6)
得到:
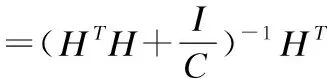
(7)
(8)
其中I為單位矩陣,C為正則化因子.
2.2 AE
AE最早由Rumelhart于1986年提出[13],其主要目的是對于一給定的數據集學習壓縮的或分布式的特征表達[14].AE是一種典型的單隱層前饋神經網絡,其期望輸出恰好等于輸入,即T=X.訓練AE的方法主要有向后傳播算法(BP)和基于ELM的方法[8].前者通過逐步迭代來不斷修改網絡參數,后者則是隨機初始化輸入權值和閾值,通過最小二乘法[15]計算得到輸出權值.后者具有精度高、訓練時間短等優點,因此本文采用該方法表達輸入數據的特征.計算其輸出權值的表達式式(9)所示.
(9)
2.3 C2ELM
C2ELM與ELM-AE的不同之處是:C2ELM先將訓練樣本按標簽進行劃分,再將每類訓練數據通過AE,得到的輸出矩陣初始化為ELM輸入權值的某個分塊矩陣[9];ELM-AE則是將所有訓練數據通過AE,得到的輸出矩陣初始化為ELM的整個輸入權值矩陣[8].
雖然C2ELM的分類精度只比ELM-AE高出一點,但其訓練時間遠小于ELM-AE.原因在于對類別樣本數據進行自動編碼時,大大降低了內存的使用,從而加快了AE的過程.
2.4 ML-ELM
ML-ELM將ELM-AE進行堆疊,構造了一個多層神經網絡[8].ML-ELM的構造過程如下:先將原始訓練樣本通過AE,把輸出權值初始化為第一層的連接權值,然后把第二層神經元的輸出信息通過AE,把計算得到的輸出權值初始化為第二層連接權值,以此類推,直到構建完只剩最后一層連接權值為止,最后一層的連接權值可由式(8)得到.第j層神經元的輸出可用式(10)表示:
Hj=g((βj)THj-1)
(10)
其中j≥1,訓練樣本輸入X可看成是第0層輸出H0.此外,訓練每層連接權值的AE的輸入權值和閾值是正交的,即滿足:
aTa=I,bTb=1
(11)
其中a=[a1,…,ak]為正交隨機輸入權值,b=[b1,…,bk]為正交隱層閾值.
3 RF-C2ELM
在ELM中,稀疏的輸入權值可以有效提高模型的預測精度.在手寫數字分類中,文獻[10]采用隨機選取圖像矩形區域來初始化ELM的輸入權值,控制矩形區域內的圖像信息保持不變,區域外的圖像信息全部置0.輸入權值ω1=[ω1,ω2,…,ωk]T的每一行ωi向量都是每個隱層結點選取圖像矩形塊后將區域外的信息置0再轉換成行向量的結果.但是,將原始的圖像信息初始化為輸入權值并不能很好地表達該類數據的特征.因此,本節介紹一種基于LAE的類限制超限學習機.
3.1 算法描述
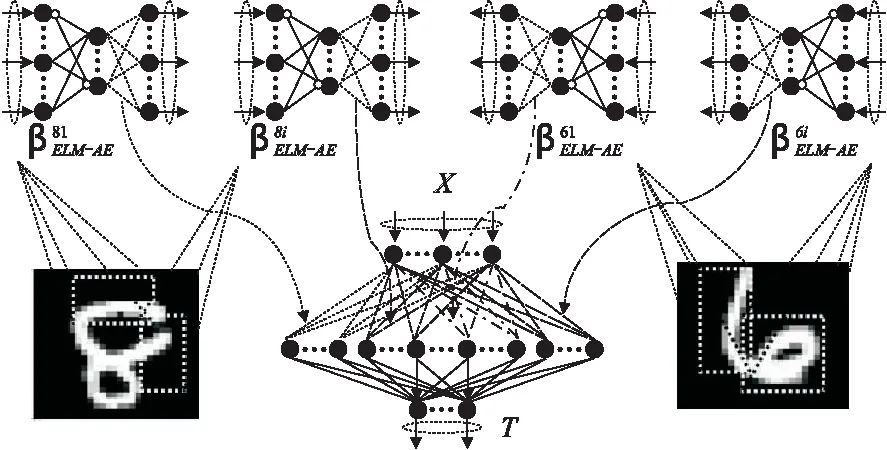
圖1 RF-C2ELM結構示意圖
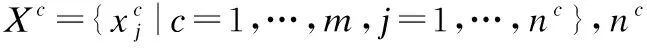
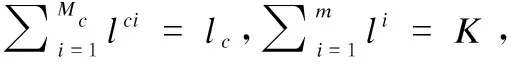
(12)
RF-C2ELM結構示意圖如圖1所示.
算法過程描述如下:
輸入:訓練樣本{(xi,ti)|i=1,…,N},ELM隱層結點數K.
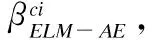
Step1. 標準化訓練樣本,在-1到1之間按均勻分布隨機初始化隱層結點的閾值b,T=?.
Step2. 根據隱層結點數K為每類的每個AE隨機選擇矩形域集合T,按面積比例分配隱層結點數.
Step3. 對于每個矩形域,從所有輸入樣本中獲得屬于該類的樣本xc,根據矩形域的范圍將域外的數據置0.
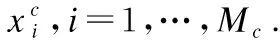
Step5. 利用公式(9)得到AE的輸出權值βELM-AE.
Step6. 利用公式(12)合并ELM的輸入權值WELM.
Step7. 利用公式(3)計算ELM的輸出矩陣H.
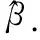
3.2 時間復雜度的比較與分析
為了突出ELM-AE、C2ELM和RF-C2ELM三種算法在訓練時間上的差異,這一小節比較三種算法在初始化ELM輸入權值上的時間復雜度.
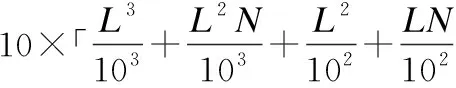
4 多層ELM
為了驗證所提出的RF-C2ELM是否較好地提取了訓練樣本的特征,這一節將C2ELM與RF-C2ELM都擴展為多層ELM,并連同ML-ELM作預測性能的比較.
為了使圖像分類精度更高,不同算法的實現在某些細節上存在著差異,比如AE輸入權值和閾值是否正交和ELM第一層輸出是否增加閾值.具體差異詳見表1.
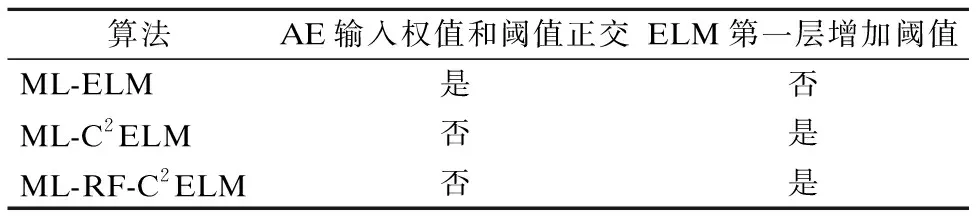
表1 三種算法在實現上的差異
另外,C2ELM并不是完全按類訓練數據,而是附加了一個所有訓練樣本參與計算的權值[9],而ML-C2ELM與ML-RF-C2ELM則是完全按類訓練數據,直接將每類訓練樣本交給單個或多個AE訓練,從而在最大內存占用率和訓練時間上獲得更多性能的提升.
5 實驗結果
實驗執行的環境是windows 7操作系統上的MATLAB R2010b,計算機內核i5-6500@3.2GHz,內存8G.
MNIST手寫數字集是測試ELM最常用的數據集.MNIST由60000個訓練樣本和10000個測試樣本組成,每個樣本的輸入數據由784個像素組成,共10類.
圖2是單隱層ELM在MNIST測試集上的誤差率.從圖中不難看出,ELM-AE、C2ELM和RF-C2ELM的誤差率遠小于隨機初始化參數的ELM,而且RF-C2ELM的誤差率明顯小于ELM-AE和C2ELM,說明該算法在淺層(即三層)神經網絡下提取到了更好的特征.
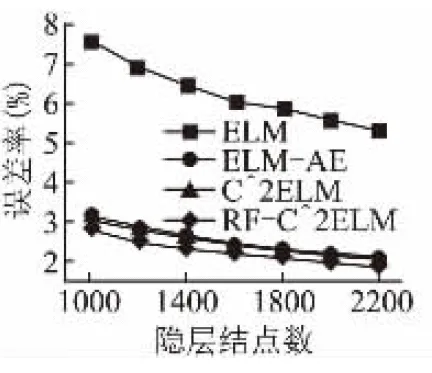
圖2 網絡結構為“784-?-10”的測試集誤差
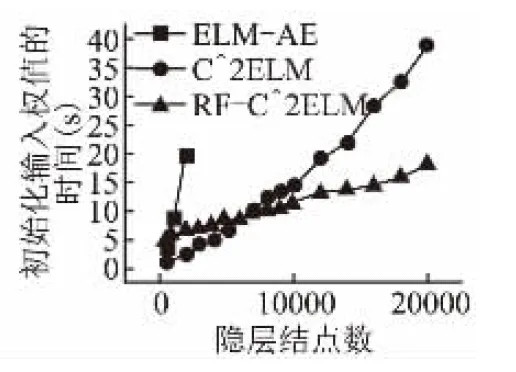
圖3 單隱層輸入權值的訓練時間隨隱層結點數的變化
為了驗證優化的第一層連接權值是否能有效逐層傳遞特征,下文將重點放在多層ELM上.接下來的實驗以4層神經網絡為例,即雙隱層前饋神經網絡,其中輸入層結點數為784,第二層結點數固定為700,第三層結點數可調,輸出層結點數為10.網絡結構可表示為784-700-?-10,“?”表示該層結點數可調.圖3記錄了訓練輸入權值的時間隨隱層結點數的變化.我們可以得到以下結論:RF-C2ELM初始化ELM輸入權值的時間基數較大,但隨隱層結點增長的速度較慢.當隱層結點數較少時,RF-C2ELM的訓練時間較長,但當隱層結點數大約超過7000時,RF-C2ELM則是三種算法中效率最高的.由于單臺計算機內存有限,為了使可調的結點數達到更高的上限,在多層ELM上采用在線序列學習[17]的方式,將數據分批訓練,可調結點數最高可達6000.MNIST測試集與訓練集在784-700-?-10結構下的誤差率分別如圖4和圖5所示.
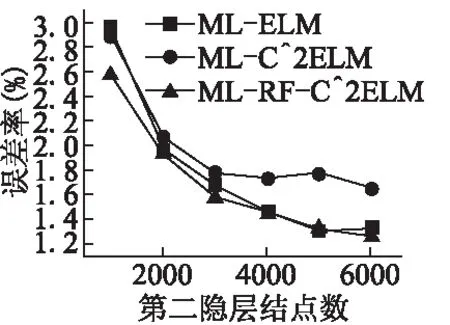
圖4 網絡結構為“784-700-?-10”下的測試誤差率
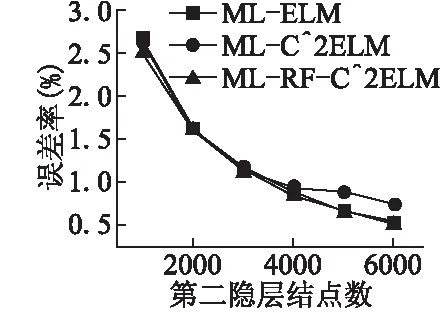
圖5 網絡結構為“784-700-?-10”下的訓練誤差率
表2列出了三種算法在網絡結構為“784-700-6000-10”下的測試集誤差率,表中Ri表示初始化第i層連接權值的AE的正則化因子,其中i∈{1,2},R3表示計算ELM輸出權值的正則化因子.從圖表可以看出ML-RF-C2ELM的預測精度最高,說明該算法能有效提取特征并進行特征逐層傳遞.

表2 網絡結構為“784-700-6000-10”下的測試誤差率
6 結 語
本文提出了一種基于LAE的類限制ELM,將其同C2ELM一起擴展到多層神經網絡,目的是為了驗證該方法的特征提取能力和逐層傳遞能力.實驗結果表明,ML-RF-C2ELM在圖像分類問題上能保持較高的預測精度.

