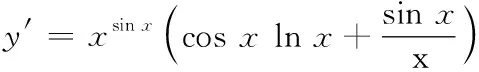淺談計算一元函數的導數方法

張志會

(武昌工學院,湖北 武漢 430065)

一元函數的微積分，所討論的均是單變量函數，在解決實際問題時，僅知道變量間的函數關系是不夠的，有時還需要知道變量變化的快慢程度。例如，物體運動的速度，城市人口增長速度等。因此為了準確地說明這些問題，就引入導數的概念。數學中研究導數、微分及其應用的部分稱為微分學，研究不定積分、定積分及其應用的部分稱為積分學。微分學與積分學統稱為微積分學。微積分學是高等數學最基本、最重要的組成部分，是現代數學許多分支的基礎。微分學是微積分的重要組成部分，它的基本概念是導數與微分，其中導數反映出函數相對于自變量的變化而變化的快慢程度，而微分則指明當自變量有微小變化時，函數值變化的近似值。本文主要闡述了在計算一元函數的導數時，討論計算一元函數的多種導數的方法。

例1設y=e-x，求y′

解令u=-x，則y=eu，從而

=eu(-1)=-e-x.

即 (e-x)′=-e-x.

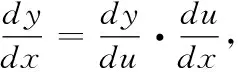
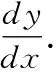
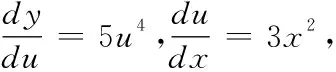
=15x2(x3-2)4．

對復合函數的復合過程能正確掌握后，可以不必寫出中間變量，只要記住復合過程，就可進行復合函數的導數計算.

例3設y=arc sin[2cos(x-1)],求y′

解y′={arc sin[2cos(x-1)]}′

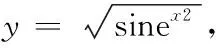
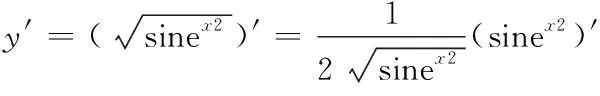
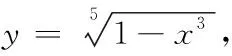
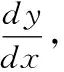
解由于ey可看作是以y為中間變量的復合函數，運用復合函數求導法則，在方程兩端對x求導，得

y+xy′-ex+ey·y′=0

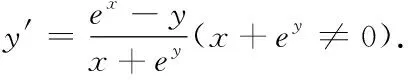
為求y′|x=0，先把x=0代入方程xy-ex+ey=0得y(0)=0

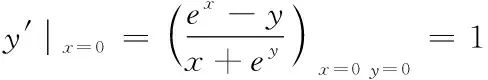
在計算冪指函數的導數以及某些乘冪、連乘積、帶根號函數的導數時，可以采用先取對數再求導的方法，簡稱對數求導法。

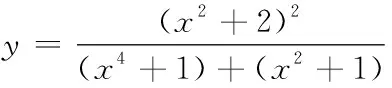
解先在兩邊取對數，得

lny=2ln(x2+2)-ln(x4+1)-ln(x2+1).

上式兩邊對x求導，注意到y是x的函數，得

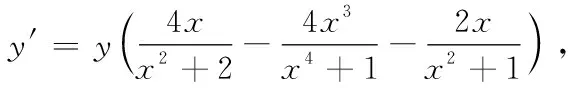
即

例7求y=xsin x(x>0)的導數

解兩邊取對數得lny=sinxlnx，兩邊對x求導，得